「最大子段和系列」GSSX - Can you answer these queries I ~ ? (持续更新...)

\(\text{SPOJ}\) 毒瘤的数据结构系列, 值得一做.

GSS题目汇总 :

GSS I :

给定一数列\(A\), 支持查询区间最大子段和
\(A[i] \le 15007,\ N\le 5e4\)

对于区间 \([L,R]\) 的最大子段和的位置, 有下列三种情况 :

位于左子区间, 即 \([L, mid]\) 中.
位于右子区间, 即 \([mid + 1, R]\) 中.
横跨左右区间, 由左区间的后缀和右区间的前缀拼接而成.

显然可以用线段树操作. 用线段树维护区间和, 最大前缀和, 最大后缀和, 最大区间子段和即可.

当左右两区间合并时 :

区间和直接累加
最大区间子段和按照上述方式构造, 并取最大值
最大前缀和 = \(\max(\) 左最大前缀, 左全部 + 右最大前缀 \()\)
最大后缀和 = \(\max(\) 右最大前缀, 右全部 + 左最大后缀 \()\)

维护线段树中每一区间的上述信息.
对于查询的区间, 向下深入分解, 按照上述方式递归合并, 即得答案.

线段树常规做法 :

//知识点:线段树 
/*
By:Luckyblock
*/
#include <cstdio>
#include <cctype>
#include <algorithm>
#define max std::max
#define ls (now << 1)
#define rs (now << 1 | 1)
const int MARX = 5e4 + 10;
//===========================================================
struct SegmentTree
{
	int L, R;
	int Pre, Suf; //[L,R]的最大 前缀和, 后缀和 
	int Sum, Marx;//[L,R]的和, 最大子段和 
} Tree[MARX << 2];
int N, M, A[MARX];
//===========================================================
inline int read()
{
    int f = 1, w = 0; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = -1;
    for(; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
    return f * w;
}
void Updata(int now) //信息上传 
{
	Tree[now].Sum = Tree[ls].Sum + Tree[rs].Sum; //更新元素和 
	
	Tree[now].Marx = max(Tree[ls].Marx, Tree[rs].Marx); //更新 最大子段和 
	Tree[now].Marx = max(Tree[now].Marx, Tree[ls].Suf + Tree[rs].Pre);
	
	Tree[now].Pre = max(Tree[ls].Pre, Tree[ls].Sum + Tree[rs].Pre); //前缀
	Tree[now].Suf = max(Tree[rs].Suf, Tree[ls].Suf + Tree[rs].Sum); //后缀 
}
void Build(int now, int L, int R) //建树 
{
	Tree[now].L = L, Tree[now].R = R;
	if(L == R) //叶节点 赋初值 
	{
	  Tree[now].Pre = Tree[now].Suf = Tree[now].Sum = Tree[now].Marx = A[L];
	  return ;
	}
	int mid = (L + R) >> 1;
	Build(ls, L, mid), Build(rs, mid + 1, R);
	Updata(now);
}
SegmentTree Merge(SegmentTree L, SegmentTree R) //将相邻查询区间L与R的信息进行合并 
{
	SegmentTree ret;
	ret.Sum = L.Sum + R.Sum; //元素和 
	ret.Marx = max(L.Marx, max(R.Marx, L.Suf + R.Pre)); //最大子段和 
	ret.Pre = max(L.Pre, L.Sum + R.Pre); //前缀 
	ret.Suf = max(R.Suf, L.Suf + R.Sum); //后缀 
	return ret;
}
SegmentTree Query(int now, int L, int R) //查询 [L,R]的最大子段和 
{
	if(L <= Tree[now].L && Tree[now].R <= R) return Tree[now]; //被全部包含 
	int mid = (Tree[now].L + Tree[now].R) >> 1;
	if(L > mid) return Query(rs, L, R); //查询区间 只位于右子树 
	if(R <= mid) return Query(ls, L, R);//查询区间 只位于左子树 
	return Merge(Query(ls, L, R), Query(rs, L, R)); //将左右区间合并 
}
//===========================================================
int main()
{
	N = read(); for(int i = 1; i <= N; i ++) A[i] = read();
	Build(1, 1, N);
	M = read();
	for(int i = 1, L, R; i <= M; i ++)
	  L = read(), R = read(), 
	  printf("%d\n", Query(1, L, R).Marx);
	return 0;
}

GSS II :

给定一数列\(A\), 支持查询区间最大子段和, 重复的数只做一次贡献
\(A[i] \in [- 1e5, 1e5],\ N, Q\le 5e4\)

做过 [SDOI2009]HH的项链之后, 提到去重就想到离线操作. 先将询问离线, 并按右端点排序.
初始时数列中没有元素, 每次将最右侧的元素加入数列, 并更新各数据.

设当前全局右端点移动到 \(R\), 第\(1\sim R\)个线段树叶节点维护 \([i,\ R]\) 的不重复元素和.

对于修改操作 :

显然 , 当右端点更新至 \(R + 1\) 时, 只有没有 \(A[R + 1]\) 的区间的叶节点的值受影响.
若 \(Pre[i]\) 表示与第\(i\)个数左侧与其相同的数的位置,
则 \([Pre[A[R + 1]] + 1,\ R + 1 ]\) 的不重复区间和 \(+\!\!= A[R+1]\)

对于查询操作:

可发现, 随着右端点右移, 第\(i\)个叶节点储存过: \(i \sim [i,\ R]\)的不重复和
而 "\(i \sim [i,\ R]\)的不重复和" 的最大值, 即以\(i\) 为起点最大不重复元素子段和.

则对每一叶节点, 都维护"历史最大不重复和".
当全局右端点移至\(R\)时, 即可回答询问\([L,\ R]\),
答案即为 \(\max\limits_{i=L}^{R}{叶节点历史最大不重复和}\).

上述操作, 即为区间加和区间取最值操作, 显然可用线段树,
维护区间不重复和, 区间历史最大不重复和, 区间加标记, 区间历史最大加标记, 来实现.

为什么要维护区间历史最大加标记 \(?\)
区间历史最大不重复和是区间不重复和的最值.
若每次修改时, 都将其更新, 则需先求得区间不重复和, 并取 \(\max\), 时间上就会有很大损耗.

所以对其单独记录一区间加标记, 来记录最大的区间加标记,
将最大不重复和与最大加标记相加, 以快速得到最大区间不重复和

上述标记详细更新过程见代码, 比较通俗易懂.
一定注意标记更新的顺序.

//知识点:线段树 
/*
By:Luckyblock
*/
#include <cstdio>
#include <cctype>
#include <algorithm>
#define ls (now << 1)
#define rs (now << 1 | 1)
#define max std::max
#define ll long long
const int INF = 1e9 + 7;
const int MARX = 1e5 + 10;
//===========================================================
struct QUERY
{
	int L, R, ID;
} Q[MARX];
struct SegmentTree
{
	int L, R;
	int Sum, HisMax; //当前区间和, 历史最大区间和
	int LazySum, LazyMax;//求和标记, 历史最大区间和标记 
} Tree[MARX << 2];
int N, M, A[MARX], Ans[MARX], Pre[MARX << 1], Last[MARX << 1];
//===========================================================
inline int read()
{
    int f = 1, w = 0; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = -1;
    for(; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
    return f * w;
}
bool CMP(QUERY first, QUERY second) {return first.R < second.R;}  
void PushUp(int now) //更新Tree[now]
{
	Tree[now].Sum = max(Tree[ls].Sum, Tree[rs].Sum); //区间和
	Tree[now].HisMax = max(Tree[ls].HisMax, Tree[rs].HisMax); //历史最大区间和 
}
void PushDown(int now) //上传信息 
{
	int LazySum = Tree[now].LazySum, LazyMax = Tree[now].LazyMax;
	Tree[now].LazySum = Tree[now].LazyMax = 0;
	
	Tree[ls].HisMax = max(Tree[ls].HisMax, Tree[ls].Sum + LazyMax); //历史最大区间和 
	Tree[ls].Sum += LazySum; //更新区间和 
	Tree[ls].LazyMax = max(Tree[ls].LazyMax, Tree[ls].LazySum + LazyMax); //历史最大区间和标记 
	Tree[ls].LazySum += LazySum; //求和和标记 
	
	Tree[rs].HisMax = max(Tree[rs].HisMax, Tree[rs].Sum + LazyMax);
	Tree[rs].Sum += LazySum;
	Tree[rs].LazyMax = max(Tree[rs].LazyMax, Tree[rs].LazySum + LazyMax);
	Tree[rs].LazySum += LazySum;
}
void Build(int now, int L, int R) //建树 
{
	Tree[now].L = L, Tree[now].R = R;
	if(L == R) return ;
	int mid = (L + R) >> 1;
	Build(ls, L, mid), Build(rs, mid + 1, R);
}
void Change(int now, int L, int R, int Val) //区间加 
{
	if(L <= Tree[now].L && Tree[now].R <= R)
	{
	  Tree[now].Sum += Val, Tree[now].LazySum += Val; //更新区间和 及 标记 
	  Tree[now].HisMax = max(Tree[now].HisMax, Tree[now].Sum); //更新历史最大区间和 
	  Tree[now].LazyMax = max(Tree[now].LazyMax, Tree[now].LazySum); //更新历史最大求和和标记 
	  return ;
	}
	PushDown(now);
	int mid = (Tree[now].L + Tree[now].R) >> 1;
	if(L <= mid) Change(ls, L, R, Val);
	if(R > mid) Change(rs, L, R, Val);
	PushUp(now);
}
int Query(int now, int L, int R) //区间查询 历史最大区间和 
{
	if(L <= Tree[now].L && Tree[now].R <= R) return Tree[now].HisMax; 
	PushDown(now);
	int mid = (Tree[now].L + Tree[now].R) >> 1, ret = - INF; 
	if(L <= mid) ret = max(ret, Query(ls, L, R));
	if(R > mid) ret = max(ret, Query(rs, L, R));
	return ret;
}
void Prepare() //预处理 
{
	N = read(); 
	for(int i = 1; i <= N; i ++) 
	  A[i] = read(), //求得 A[i]在i之前一次出现的位置 
	  Pre[i] = Last[A[i] + MARX], Last[A[i] + MARX] = i;
	Build(1, 1, N);
	
	M = read(); //离线询问并排序 
	for(int i = 1; i <= M; i ++) 
	  Q[i].ID = i,
	  Q[i].L = read(), Q[i].R = read();
	std :: sort(Q + 1, Q + M + 1, CMP);
}
//===========================================================
int main()
{
	Prepare();
	for(int i = 1, j = 1; i <= N; i ++)
	{
	  Change(1, Pre[i] + 1, i, A[i]); //修改 会被影响的区域 
	  for(; Q[j].R <= i && j <= M; j ++) Ans[Q[j].ID] = Query(1, Q[j].L, Q[j].R); 
	}
	for(int i = 1; i <= M; i ++) printf("%d\n", Ans[i]);
    return 0;
}

GSS III :

给定一数列\(A\), 支持单点修改 , 查询区间最大子段和
\(A[i] \in [- 1e4, 1e4],\ N, Q\le 5e4\)

带单点修改的 GSSI.
直接修改线段树叶节点信息即可, 直接上代码 :

//知识点:线段树 
/*
By:Luckyblock
*/
#include <cstdio>
#include <cctype>
#include <algorithm>
#define max std::max
#define ls (now << 1)
#define rs (now << 1 | 1)
const int MARX = 5e4 + 10;
//===========================================================
struct SegmentTree
{
	int L, R;
	int Pre, Suf; //[L,R]的最大 前缀和, 后缀和 
	int Sum, Marx;//[L,R]的和, 最大子段和 
} Tree[MARX << 2];
int N, M, A[MARX];
//===========================================================
inline int read()
{
    int f = 1, w = 0; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = -1;
    for(; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
    return f * w;
}
void Updata(int now) //信息上传 
{
	Tree[now].Sum = Tree[ls].Sum + Tree[rs].Sum; //更新元素和 
	
	Tree[now].Marx = max(Tree[ls].Marx, Tree[rs].Marx); //更新 最大子段和 
	Tree[now].Marx = max(Tree[now].Marx, Tree[ls].Suf + Tree[rs].Pre);
	
	Tree[now].Pre = max(Tree[ls].Pre, Tree[ls].Sum + Tree[rs].Pre); //前缀
	Tree[now].Suf = max(Tree[rs].Suf, Tree[ls].Suf + Tree[rs].Sum); //后缀 
}
void Build(int now, int L, int R) //建树 
{
	Tree[now].L = L, Tree[now].R = R;
	if(L == R) //叶节点 赋初值 
	{
	  Tree[now].Pre = Tree[now].Suf = Tree[now].Sum = Tree[now].Marx = A[L];
	  return ;
	}
	int mid = (L + R) >> 1;
	Build(ls, L, mid), Build(rs, mid + 1, R);
	Updata(now);
}
SegmentTree Merge(SegmentTree L, SegmentTree R) //将相邻区间L与R的信息进行合并 
{
	SegmentTree ret;
	ret.Sum = L.Sum + R.Sum; //元素和 
	ret.Marx = max(L.Marx, max(R.Marx, L.Suf + R.Pre)); //最大子段和 
	ret.Pre = max(L.Pre, L.Sum + R.Pre); //前缀 
	ret.Suf = max(R.Suf, L.Suf + R.Sum); //后缀 
	return ret;
}
SegmentTree Query(int now, int L, int R) //查询 [L,R]的最大子段和 
{
	if(L <= Tree[now].L && Tree[now].R <= R) return Tree[now]; //被全部包含 
	int mid = (Tree[now].L + Tree[now].R) >> 1;
	if(L > mid) return Query(rs, L, R); //查询区间 只位于右子树 
	if(R <= mid) return Query(ls, L, R);//查询区间 只位于左子树 
	return Merge(Query(ls, L, R), Query(rs, L, R)); //将左右区间合并 
}
void Change(int now, int Pos, int Val) //单点修改 
{
	if(Tree[now].L == Tree[now].R && Tree[now].L == Pos) //向下深入至 叶节点 
	{
	  Tree[now].Pre = Tree[now].Suf = Tree[now].Sum = Tree[now].Marx = Val;
	  return ;
	}
	int mid = (Tree[now].L + Tree[now].R) >> 1;
	if(Pos <= mid) Change(ls, Pos, Val);
	else Change(rs, Pos, Val);
	Updata(now);
}
//===========================================================
int main()
{
	N = read(); for(int i = 1; i <= N; i ++) A[i] = read();
	Build(1, 1, N);
	M = read();
	for(int i = 1; i <= M; i ++)
	{
	  int opt = read(), L = read(), R = read();
	  if(opt == 0) Change(1, L, R);
	  else printf("%d\n", Query(1, L, R).Marx);	
	} 
	return 0;
}

这玩意显然可以 \(DP\).
对于每一查询区间 \([L,\ R]\), 设 \(f[i]\) 表示从 \(L \sim i\) 内包含\(i\)的最大子段和.
显然有转移方程 : \(f[i] = max(f[i - 1] + A[i], A[i])\)
每次询问都更新\(f\), \(\ \max\limits_{i=L}^{R}{f[i]}\) 即为本次查询答案.
复杂度\(O(nm)\)

似乎可以动态 \(DP\ ?\) 学了之后再更 .

GSS IV :

给定一数列\(A\), 支持区间开平方操作, 查询区间和
\(\sum\limits_{i=1}^{N} A[i] \le 10^{18},\ N, M \le 1e5\)

分块经典操作 , 但是此题卡掉了分块 ,
将分块思想应用至线段树.

由于开方运算不满足一系列运算律, 无法使用标记法.

怎么办 \(?\) 考虑直接暴力.
众所周知, \(\Bigg\lfloor\sqrt{\sqrt{\sqrt{\sqrt{\sqrt{\sqrt {10 ^{18}}}}}}}\Bigg\rfloor = 1\) .
对于一个正数, 最多 \(6\) 次修改后必然等于 \(1\).
而 \(\sqrt{1} = 1\) , 修改操作对其不会有影响 .

则可以记录各某区间的开方次数.
若开方次数 \(> 5\), 则无论其修改次数, 元素和都不会改变, 不进行修改操作.
否则直接深入到叶节点暴力修改, 并在暴力修改时完成对次数的更新.

//知识点:线段树 
/*
By:Luckyblock
*/
#include <cstdio>
#include <cctype>
#include <cmath>
#include <cstring>
#include <algorithm>
#define ls (now << 1)
#define rs (now << 1 | 1)
#define ll long long
const int MARX = 1e5 + 10;
//===========================================================
struct SegmentTree
{
	int L, R, Num;
	ll Sum;
} Tree[MARX << 2];
int N, M, T;
ll Original[MARX];
//===========================================================
inline ll read()
{
    ll f = 1, w = 0; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = -1;
    for(; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
    return f * w;
}
void PushUp(int now) {Tree[now].Sum = Tree[ls].Sum + Tree[rs].Sum;} //更新区间和 
void Build(int now, int L, int R) //建树 
{
	Tree[now].L = L, Tree[now].R = R;
	if(L == R) {Tree[now].Sum = (ll) Original[L]; return ;}
	int mid = (L + R) >> 1;
	Build(ls, L, mid), Build(rs, mid + 1, R);
	PushUp(now);
}
void Change(int now, int L, int R) //区间修改 
{
	if(Tree[now].Num > 5) return ; //已全为1, 不需修改 
	if(L <= Tree[now].L && Tree[now].R <= R)
	{
	  Tree[now].Num ++; //更新开方次数 
	  if(Tree[now].L == Tree[now].R) //若为叶节点. 暴力修改 
	  {
	  	Tree[now].Sum = sqrt(Tree[now].Sum);
	  	return ;
	  }
	}
	int mid = (Tree[now].L + Tree[now].R) >> 1;
	if(L <= mid) Change(ls, L, R);
	if(R > mid) Change(rs, L, R);
	PushUp(now);
}
ll Query(int now, int L, int R) //查询区间和 
{
	if(L <= Tree[now].L && Tree[now].R <= R) return Tree[now].Sum;
	int mid = (Tree[now].L + Tree[now].R) >> 1;
	ll ret = 0;
	if(L <= mid) ret += Query(ls, L, R);
	if(R > mid) ret += Query(rs, L, R);
	return ret;
}
//===========================================================
int main()
{
	while(scanf("%d", &N) != EOF)
    {
	  memset(Tree, 0, sizeof(Tree)); printf("Case #%d:\n", ++ T);
      for(int i = 1; i <= N; i ++) Original[i] = read();
      Build(1, 1, N);
      M = read();
      while(M --)
      {
      	int opt = (int) read(), x = (int) read(), y = (int) read();
      	if(x > y) std :: swap(x, y);
      	if(! opt) Change(1, x, y);
      	else printf("%lld\n", Query(1, x, y));
      }
      printf("\n");
    }
    return 0;
}

GSS V :

给定一数列 \(A\), \(M\)次查询, 每次给定 \(x_1, y_1, x_2, y_2\) \((\)满足\(x_1\le x_2, y_1\le y_2)\).
查询左端点在\([x_1, y_1]\), 右端点在\([x_2,y_2]\)的区间的的最大子段和.
多组数据, 数据组数 \(\le 5\), \(N, M\le1e4\), \(A[i]\in[-1e4,1e4]\).

按照查询区间的关系进行分类讨论:

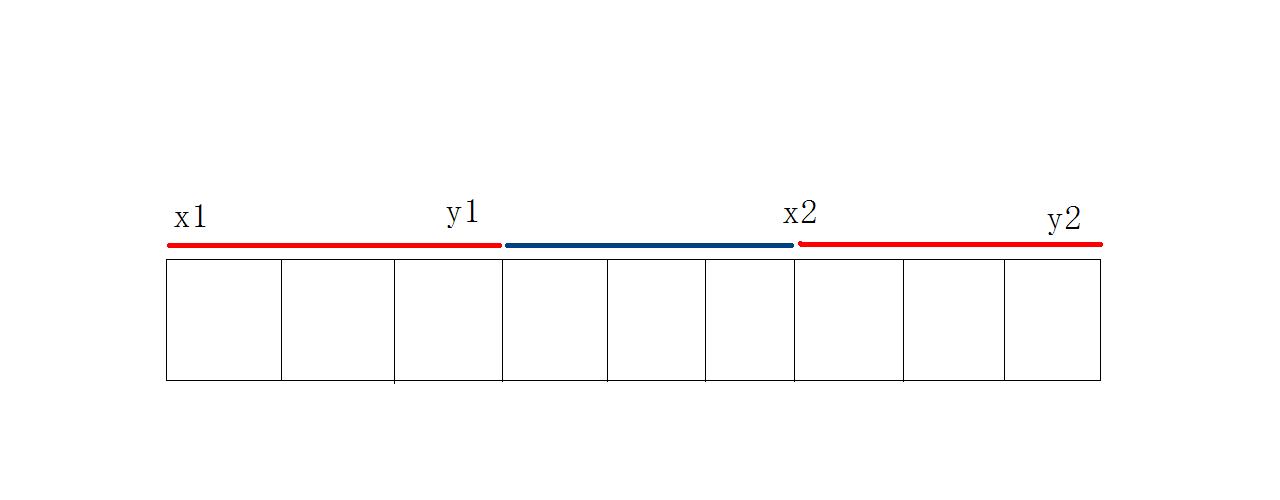
两区间相离, 即 \(y_1 < x_1 - 1:\)

不论左右端点位置, \([y_1+1,x_2-1]\)\((\)即中间蓝色部分\()\) 必被包含.
欲最大化子段和, 只能调整被选择区间前缀与后缀.

显然, 当取\([x_1,y_1]\)的最大后缀, \([x_2,y_2]\)的最大前缀时, 组合得到的区间和最大.
此类情况答案即为: \([x_1,y_1]\)最大后缀和 \(+\)\([y_1 + 1, x_2-1]\)区间和\(+\) \([x_2,y_2]\)最大前缀和
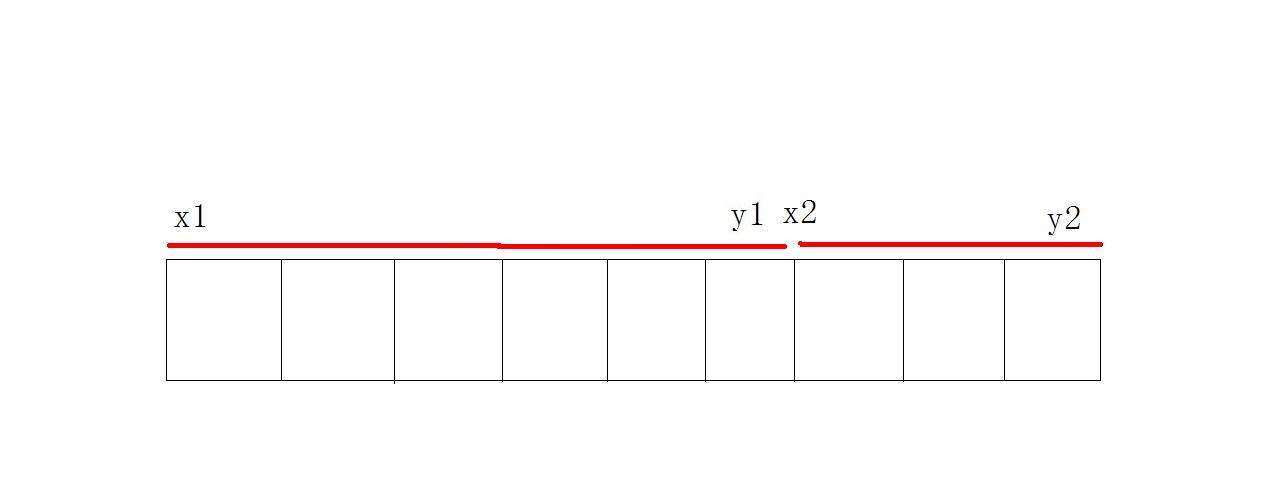
两区间相邻, 即\(y_1=x_1-1\)

显然此类情况答案为: \([x_1,y1]\)最大后缀和 \(+\) \([x_2,y_2]\)最大前缀和
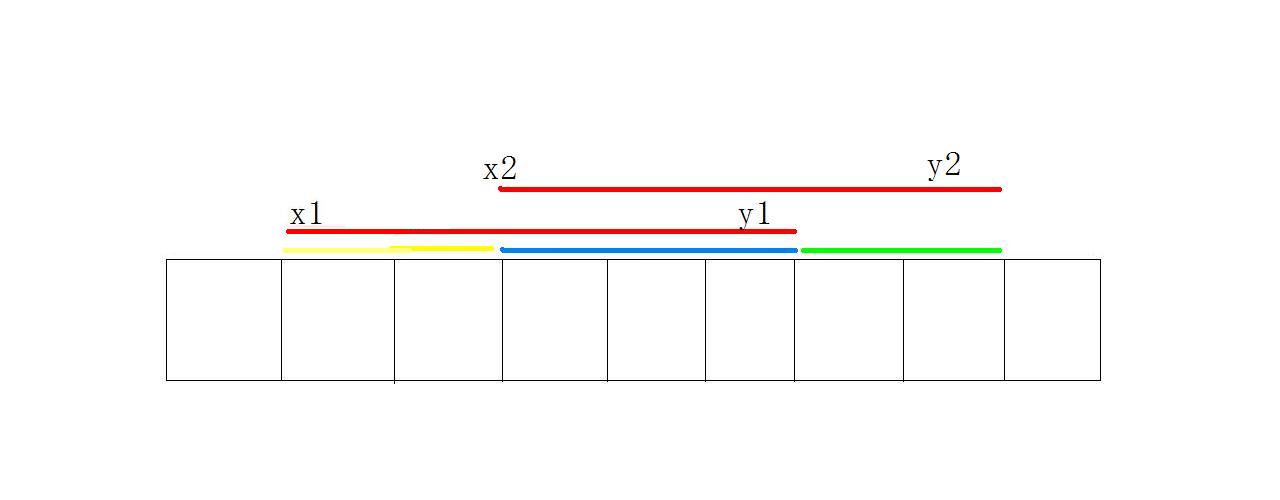
两区间相交, 即\(y_1 \ge x_2\)
- 两端都位于 \([x_2,y_1]\)中时, 即GSSI, 答案为 \([x_2,y_1]\)的最大子段和.
- 左端位于 \([x_1,x_2-1]\) \((\)即黄色区域\()\), 右端点位于 \([x_2,y_2]\)时,
  显然, 答案即为 : \([x_1,x_2-1]\)最大后缀和 \(+\) \([x_2,y_2]\)最大前缀和.
- 右端位于 \([y_1+1,y_2]\) \((\)即绿色区域\()\), 左端点位于 \([x_1,y_1]\)时,
  显然, 答案即为 : \([x_1,y_1]\)最大后缀和 \(+\) \([y_1+1,y_2]\)最大前缀和.
对上述值取 \(max\)即可.

通过上述分析发现, GSSV 和GSSI基本相同,除主函数外一模一样.
只需要根据区间关系分类讨论即可.

//知识点:线段树 
/*
By:Luckyblock
*/
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#define ll long long
#define max std::max
#define ls (now << 1)
#define rs (now << 1 | 1)
const int INF = 1e9 + 2077;
const int MARX = 1e4 + 10;
//===========================================================
struct SegmentTree
{
	int L, R;
	int Pre, Suf; //[L,R]的最大 前缀和, 后缀和 
	int Sum, Max;//[L,R]的和, 最大子段和 
} Tree[MARX << 2], Inf = (SegmentTree){-INF, -INF, -INF, -INF, -INF, -INF};
int T, N, M, A[MARX];
//===========================================================
inline int read()
{
    int f = 1, w = 0; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = -1;
    for(; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
    return f * w;
}
void PushUp(int now) //信息上传 
{
	Tree[now].Pre = max(Tree[ls].Pre, Tree[ls].Sum + Tree[rs].Pre); //前缀 
	Tree[now].Suf = max(Tree[rs].Suf, Tree[rs].Sum + Tree[ls].Suf); //后缀 
	Tree[now].Sum = Tree[ls].Sum + Tree[rs].Sum; //元素和 
	Tree[now].Max = max(Tree[ls].Max, max(Tree[rs].Max, Tree[ls].Suf + Tree[rs].Pre)); //最大子段和 
}
void Build(int now, int L, int R) //建树 
{
	Tree[now].L = L, Tree[now].R = R;
	if(L == R)
	{
	  Tree[now].Suf = Tree[now].Pre = A[L];
	  Tree[now].Sum = Tree[now].Max = A[L];
	  return ;
	}
	int mid = (L + R) >> 1;
	Build(ls, L, mid), Build(rs, mid + 1, R);
	PushUp(now);
}
SegmentTree Merge(SegmentTree L, SegmentTree R) //区间信息合并 
{
	SegmentTree ret;
	ret.Pre = max(L.Pre, L.Sum + R.Pre); //前缀 
	ret.Suf = max(R.Suf, L.Suf + R.Sum); //后缀 
	ret.Sum = L.Sum + R.Sum; //元素和 
	ret.Max = max(L.Max, max(R.Max, L.Suf + R.Pre)); //最大子段和 
	return ret;
}
SegmentTree Query(int now, int L, int R) //查询 [L,R]的各信息
{
	if(L > R) return Inf; //不合法的查询 
	if(L <= Tree[now].L && Tree[now].R <= R) return Tree[now]; //返回完整区间 
	int mid = (Tree[now].L + Tree[now].R) >> 1;
	if(R <= mid) return Query(ls, L, R); //查询区间 只位于右子树  
	if(L > mid) return Query(rs, L, R);//查询区间 只位于左子树  
	return Merge(Query(ls, L, R), Query(rs, L, R));//将左右区间合并  
}
//===========================================================
int main()
{
	T = read();
	while(T --)
	{
	  memset(Tree, 0, sizeof(Tree));
	  N = read(); for(int i = 1; i <= N; i ++) A[i] = read();
	  Build(1, 1, N);
	  
	  M = read(); 
	  for(int i = 1; i <= M; i ++)
	  {
	 	int L1 = read(), R1 = read(), L2 = read(), R2 = read();
	 	SegmentTree ret1 = Query(1, L1, R1), ret2 = Query(1, L2, R2), ret3; 
	 	//两区间相离: 
		if(R1 < L2 - 1) {ret3 = Query(1, R1 + 1, L2 - 1); printf("%d\n", ret1.Suf + ret3.Sum + ret2.Pre); continue;}
	 	//两区间相邻: 
		if(R1 == L2 - 1) {printf("%d\n", ret1.Suf + ret2.Pre); continue;}
	 	//两区间有重叠部分: 
		SegmentTree ret4 = Query(1, L2, R1), ret5 = Query(1, R1 + 1, R2), ret6 = Query(1, L1, L2 - 1);
	 	printf("%d\n", max(ret4.Max, max(ret1.Suf + ret5.Pre, ret2.Pre + ret6.Suf)));
	  }
	}
    return 0;
}

\(\text{Next Dream...}\)

posted @ 2020-01-04 21:47 Luckyblock 阅读(354) 评论(3) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Luckyblock

身与华落，心将香飞