「笔记」树的直径

树的直径

\[\large 扯 : \]

做 P2491 [SDOI2011]消防 的时候 ,
在寻找 距离每个点的最远点时卡住了 = =
在 题解的帮助 不懈的努力 下 , 得到了 :
距离每个点的最远点 一定为直径的 一端点 的结论
\(\text{sb}\ \text{Luckyblock}\) 并不会证 , 于是就有了这篇文章 :

树形 \(\text{DP}\)

\[\large 实现 : \]

• 随意选择 一节点为根 .
  对于每一个 树上节点 \(u\) ,
  维护 其子树中 以其为端点 的 最长链\(\text{F1}_u\) 与 次长链\(\text{F2}_u\) ,

• 显然 , 树的直径 \(=\large \max\limits_{u=1}^{n}{(\text{F1}_u + \text{F2}_u)}\)
  必然有一 直径上的点 , 其 最长链 与 次长链 连接后恰好为直径

\[\large 优缺点: \]

优点 : 简单好写
缺点 : 不易记录 树的直径的路径

\[\large 代码: \]

int dfs1(int u, int fa)
{
	int marx = 0, marx2 = 0;// 最长链,次长链 
	for(int i = head[u]; i; i = e[i].ne)
	  if(e[i].v != fa)
	  {
	  	int ret = dfs1(e[i].v, u) + e[i].w;//子节点传回的最长链 
		if(ret >= marx) {marx2 = marx , marx = ret;}//维护 最长链,次长链
	  }
	ans = max(ans, (marx+marx2));//树上最长路径= max(最长链+次长链) 
	return marx;//递归回传最长链 
}

虽然树形 \(\text{DP}\) 非常优秀 \(\dots\)
但是它并不是 此文的主角

---

两次 \(\text{DFS}\)

\[\large 实现 : \]

• 首先 , 随意选择 一个点 为根 ,
  通过 \(\text{DFS}\) 求得树上其他点 , 到达此点的距离
  距离其 最远的点 , 必然为直径的 一端点

• 以上一步中 找到的直径的端点 为根 ,
  再通过 \(\text{DFS}\) 求得树上其他点 , 到达此点的距离
  距离其最远的点 , 必然为直径的 另一端点

\[\large 证明 : \]

若证得 : 距每个点最远的点 定为直径的 一端点 , 即可证明上述算法的正确性

设直径两端点 分别为 : \(x_1 与 x_2\) ; \(d(x,y)\) 为树上两点之间 的 距离
设 \(u\) 与非直径上的点 中距离最远的 点 为 \(y\)

• 若 \(u\) 在直径上 :

  

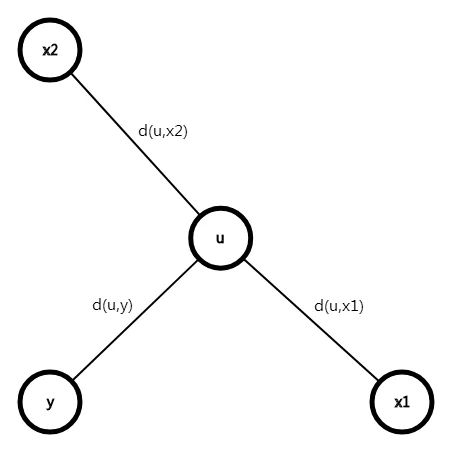
  • 设 \(d(u,x_1) > d(u,x_2)\) ,
    显然 , 有 \(d(u,x_1) > d(u,y)\)

  • 可以反证 :
    若 \(d(u,y) > d(u,x_1)\) , 则 \(d(u,x1) + d(u,y) > d(u,x1) + d(u,x2)\)
    则应选择 \(x_1\) 与 \(y\) 作为 直径 , 而非 \(x_1\) 与 \(x_2\) ,

    反证 结论正确 , 距 \(x\) 最远的点应为 \(x1\) , 而非 \(y\)

• 若 \(u\) 不在直径上 且 路径 \((u,y)\) 与 路径\((x_1,x_2)\) 有交点 \(z\) :

  

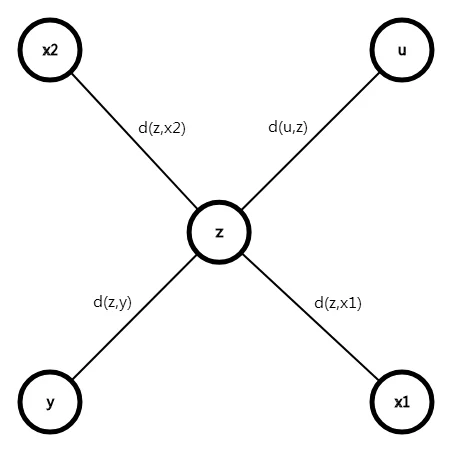
  • 设 \(d(z,x_1) > d(z,x_2)\) ,
    显然 , 有 \(d(z,x_1) > d(z,y)\)
    否则 不满足树的直径的性质

  • 则有 : \(d(u,z) + d(z,x1) > d(u,z) + d(z,y)\)
    故: 距 \(x\) 最远的点应为 \(x1\) , 而非 \(y\)

• 若 \(u\) 不在直径上 且 路径 \((u,y)\) 与 路径\((x_1,x_2)\) 无交点 :
  

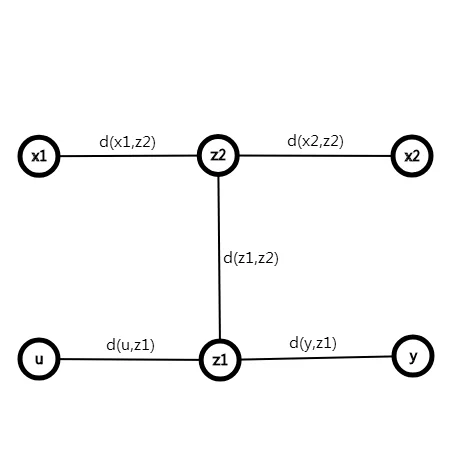
  • 设路径 \((x,y)\) 上一点 \(z1\) 与 直径上一点 \(z2\) 通过路径 \((z1,z2)\) 相连通
    设 \(d(x2,z2) > d(x1,z2)\)
    显然 , 有 : \(d(x2,z2) > d(z1,z2) + d(y,z1)\)
    否则 不满足树的直径的性质

  • 则有 : \(d(u,z1) + d(z1,z2) +d(x2,z2) > d(u,z1) + d(z1,y)\)
    故: 距 \(u\) 最远的点应为 \(x2\) , 而非 \(y\)

• \(\text{Q.E.D}\) [495...]

\[\large 代码: \]

void dfs(int now,int fat,int sum,bool flag)//dfs求得 树的直径 
{
	if(flag) pre[now] = fat, map[now] = sum;//第二次dfs记录路径 (前驱 
	dis[now] = dis[fat] + sum;//更新距离 
	for(int i = head[now]; i; i = e[i].ne)
	  if(e[i].v != fat) dfs(e[i].v,now,e[i].w,flag);
}
void get_road()//求得 树的直径 
{
	dfs(1,0,0ll,0); //一次dfs 
	for(int i = 1, maxdis = 0; i <= n; i ++)//选择 距离最远的点 
	  if(dis[i] > maxdis) u = i,maxdis = dis[i];
	dfs(u,0,0ll,1); //二次dfs 
	for(int i = 1, maxdis = 0; i <= n; i ++)//选择 距离最远的点 
	  if(dis[i] > maxdis) v = i,maxdis = dis[i];
}