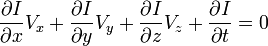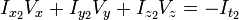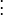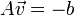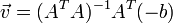LK光流算法公式详解

由于工程需要用到 Lucas-Kanade 光流，在此进行一下简单整理（后续还会陆续整理关于KCF，PCA，SVM，最小二乘、岭回归、核函数、dpm等等）：

光流，简单说也就是画面移动过程中，图像上每个像素的x，y位移量，比如第t帧的时候A点的位置是(x1, y1)，那么我们在第t+1帧的时候再找到A点，假如它的位置是(x2,y2)，那么我们就可以确定A点的运动了：(u, v) = (x2, y2) - (x1,y1)

 

1、假设原图是I(x,y,z)  (这里是扩展到三维空间的，所以还有个z值)，移动后的图像是I(x+δx,y+δy,z+δz,t+δt),两者满足:

 

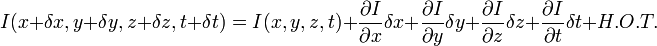
2、其中图像移动可以认为I (x ,y ,z ,t ) = I (x + δx ,y + δy ,z + δz ,t + δt )

也就是说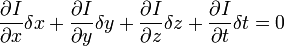：（ H.O.T. 指更高阶，在移动足够小的情况下可以忽略)

 

3、从这个方程中我们可以得到：

 

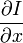
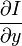
其中Vx = u， Vy=v，也就是光流的值（二维图像没有z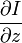），   则是图像在(x ,y,z ,t )这一点的梯度  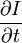（就是两帧图像块之间差值） 。

 

 

4、假设流(Vx,Vy,Vz)在一个大小为m*m*m(m>1)的小窗中是一个常数，那么从像素1...n , n = m*m*m 中可以得到下列一组方程： 

 

三个未知数但是有多于三个的方程，这个方程组自然是个超定方程，也就是说方程组内有冗余，方程组可以表示为：

也就是：

采用最小二乘法：

 

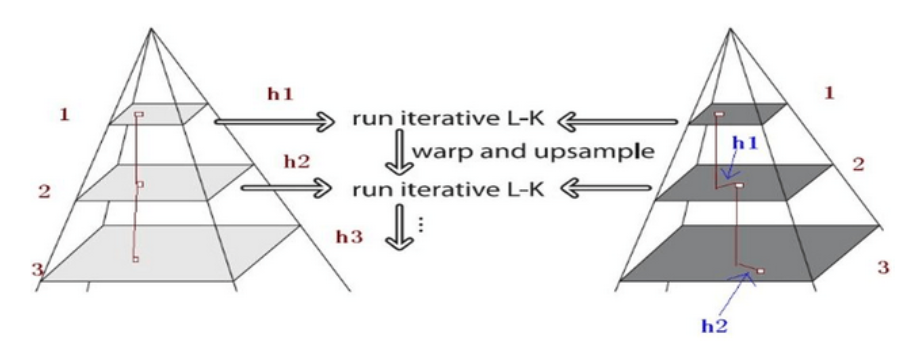
5、另外，由于LK算法假设是小位移，为了解决大位移问题，需要在多层图像缩放金字塔上求解，每一层的求解结果乘以2后加到下一层：

 

6、具体就见matlab代码：

 其中求解最小二乘的行列式求解只有2维所以计算量尚可容忍

%Data acquisition
im1= ((imread('1.png')));
im2= ((imread('2.png'))); 
im1=single(im1);
im2=single(im2); 
[result,corner_count,ptx,pty] = harris(im1);  //harris角点是求光流的关键点
imagesc(result);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%parameters : levels number, window size, iterations number, regularization
numLevels= 4;
window= 10;
iterations=3;
alpha = 0.001;

hw = floor(window/2);

t0 = clock;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%pyramids creation
pyramid1 = im1;
pyramid2 = im2;
%init
for i=2:numLevels
im1 = impyramid(im1, 'reduce');
im2 = impyramid(im2, 'reduce');
pyramid1(1:size(im1,1), 1:size(im1,2), i) = im1;
pyramid2(1:size(im2,1), 1:size(im2,2), i) = im2;
end;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Processing all levels
for p = 1:numLevels
%current pyramid
im1 = pyramid1(1:(size(pyramid1,1)/(2^(numLevels - p))), 1:(size(pyramid1,2)/(2^(numLevels - p))), (numLevels - p)+1);
im2 = pyramid2(1:(size(pyramid2,1)/(2^(numLevels - p))), 1:(size(pyramid2,2)/(2^(numLevels - p))), (numLevels - p)+1);

%init
if p==1
u = zeros(size(im1));
v = zeros(size(im1));
else
%resizing
u = 2 * imresize(u,size(u)*2,'bilinear');
v = 2 * imresize(v,size(v)*2,'bilinear');
end

%refinment loop
for r = 1:iterations

u=round(u);
v=round(v);

%every pixel loop
for i = 1+hw:size(im1,1)-hw
for j = 1+hw:size(im2,2)-hw
patch1 = im1(i-hw:i+hw, j-hw:j+hw);

%moved patch
lr = i-hw+v(i,j);
hr = i+hw+v(i,j);
lc = j-hw+u(i,j);
hc = j+hw+u(i,j);

if (lr < 1)||(hr > size(im1,1))||(lc < 1)||(hc > size(im1,2))
%Regularized least square processing
else
patch2 = im2(lr:hr, lc:hc);

fx = conv2(patch1, 0.25* [-1 1; -1 1]) + conv2(patch2, 0.25*[-1 1; -1 1]);
fy = conv2(patch1, 0.25* [-1 -1; 1 1]) + conv2(patch2, 0.25*[-1 -1; 1 1]);
ft = conv2(patch1, 0.25*ones(2)) + conv2(patch2, -0.25*ones(2));

Fx = fx(2:window-1,2:window-1)';
Fy = fy(2:window-1,2:window-1)';
Ft = ft(2:window-1,2:window-1)';

A = [Fx(:) Fy(:)];
G=A'*A;

G(1,1)=G(1,1)+alpha; G(2,2)=G(2,2)+alpha;
U=1/(G(1,1)*G(2,2)-G(1,2)*G(2,1))*[G(2,2) -G(1,2);-G(2,1) G(1,1)]*A'*-Ft(:);
u(i,j)=u(i,j)+U(1); v(i,j)=v(i,j)+U(2);
end
end
end
end
etime(clock,t0)
end