2024.9.22

今日总结:
1:数
本题目是一个用记忆化搜索来实现数位DP
dp[i][j]表示在没有顶上界和前导零的情况下，当前填到了第i位,余数为j的数的个数。
在搜索过程中记一下当前数位和mod p等于多少

点击查看代码

#include<bits/stdc++.h>

using namespace std;

const int Mod = 1e9 + 7;
const int N = 1e4 + 10;

int n,sum,ans;
int dp[N][100];
char s[N];

int main()
{
    scanf("%d%s",&n,s);
    int len = strlen(s);
    dp[0][0] = 1;
    for(int i = 1;i <= len;i ++)
        for(int j = 0;j < n;j ++)
            for(int k = 0;k <= 9;k ++)
            {
                dp[i][(j + k) % n] += dp[i - 1][j];
                dp[i][(j + k) % n] %= Mod;
            }
    for(int i = 0;i < len;i ++)
    {
        int x = s[i] ^ 48;
        for(int j = 0;j < x;j ++)
        {
            ans += dp[len - i - 1][((n << 1) - sum - j) % n];
            ans %= Mod;
        }
        sum += x;
        sum %= n;
    }
    if(sum != 0)
    {
        ans += Mod - 1;
        ans %= Mod;
    }
    printf("%d\n",ans);
    return 0;
}

2:Cosmic Rays
这道题主要考察的是最短路，有一个很重要的结论对于一个覆盖的区域来说，经过它的圆心永远比不经过圆心优，
一条边的边权就是两个点的欧几里德距离减去两个圆的半径。
最后用dijstra求一下最短路即可

点击查看代码

#include<bits/stdc++.h>

using namespace std;

const int N = 1500;
const long long INF = 1e18;

int n;
int X[N],Y[N],R[N];
double dis[N];
bool vis[N];

inline double Dist(int x,int y)
{
    return sqrt(1.*x*x + 1.*y*y);
}

int main()
{
    scanf("%d%d%d%d%d",X + 1,Y + 1,X + 2,Y + 2,&n);
    n += 2;
    for(int i = 3;i <= n;i ++)
        scanf("%d%d%d",X + i,Y + i,R + i);
    for(int i = 2;i <= n;i ++)
        dis[i] = INF;
    for(int T = 1;T < n;T ++)
    {
        int u = 0;
        for(int i = 1;i <= n;i ++)
            if((!u || dis[i] < dis[u]) && !vis[i]) u = i;
        vis[u] = 1;
        for(int i = 1;i <= n;i ++)
            if(u != i && !vis[i])
            {
                double goal = Dist(X[u] - X[i],Y[u] - Y[i]) - R[u] - R[i];
                if(goal < 0) goal = 0;
                if(dis[i] > dis[u] + goal) dis[i] = dis[u] + goal;
            }
    }
    printf("%.15f\n",dis[2] + 1e-15);
    return 0;
}

3：高橋君
这道题主要是用莫队：
首先分析题意

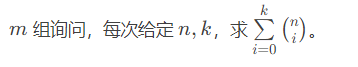
预处理出每个数的逆元、算出阶乘与阶乘的逆元的组合数

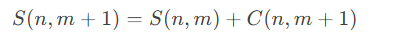
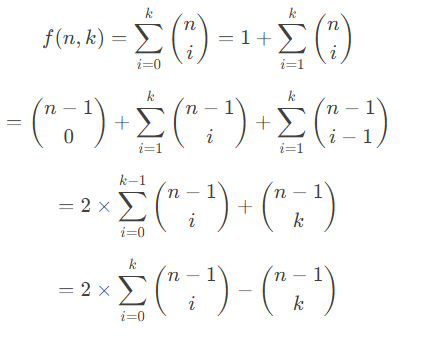
点击查看代码

#include<bits/stdc++.h>

using namespace std;

const int M = 520;
const int Mod = 1000000007;
const int N = 1e5 + 10;

#define int long long

int Mo(int x, int y)
{
    int q = 1;
    for(; y; y >>= 1, x = x * x % Mod)
        if (y & 1)
            q = q * x % Mod;
    return q;
}
struct Node
{
    int l, r, i;
}q[N];

int n,dis,z = 1;
int b[N],f[N],val[N],w[N];
inline bool Option(Node x, Node y) 
{
    return b[x.l] == b[y.l] ? b[x.l] & 1 ? x.r < y.r : x.r > y.r : x.l < y.l; 
}

int C(int x, int y) 
{
    return x < y ? 0 : f[x] * val[y] % Mod * val[x - y] % Mod; 
}

signed main()
{
    dis = Mo(2, Mod - 2);
    for(int i = f[0] = 1;i <= 1e5;i ++)
    {
        f[i] = f[i - 1] * i % Mod;
        b[i] = (i - 1) / M + 1;
    }
    val[100000] = Mo(f[100000], Mod - 2);
    for(int i = 1e5 - 1;i >= 0;i --)
        val[i] = val[i + 1] * (i + 1) % Mod;
    scanf("%lld",&n);
    for(int i = 0;i < n;i ++)
    {
        scanf("%lld%lld",&q[i].r,&q[i].l);
        q[i].i = i;
    }   
    sort(q, q + n,Option);
    for(int i = 0,l = 1,r = 0;i < n;i ++)
    {
        while(l > q[i].l)
            z = (z + Mod - C(r, l--)) % Mod;
        while(r < q[i].r)
            z = (z * 2 + Mod - C(r++, l)) % Mod;
        while(l < q[i].l)
            z = (z + C(r, ++l)) % Mod;
        while(r > q[i].r)
            z = (z + C(--r, l)) * dis % Mod;
        w[q[i].i] = z;
    }
    for(int i = 0;i < n;i ++)
        printf("%lld\n", w[i]);
    return 0;
}