数据结构
数据结构
数据结构
数据结构的定义
我们如何把现实中大量而且非常复杂的问题以特定的数据类型(个体)和特定的存储结构(个体的关系)保存到相应的主存储器(内存)中,以及在此基础上为实现某个功能而执行的相应操作,这个相应的操作也叫做算法
数据结构 == 个体 + 个体的关系
数据结构的特点
数据结构是软件中最核心的课程
程序 = 数据的存储 + 数据的操作 + 可以被计算机执行的语言
线性结构
把所有的节点用一根线串起来
数组和链表的区别
数组需要一块连续的内存空间来存储,对内存的要求比较高。如果我们申请一个 100MB 大小的数组,当内存中没有连续的、足够大的存储空间时,即便内存的剩余总可用空间大于 100MB,仍然会申请失败。 而链表恰恰相反,它并不需要一块连续的内存空间,它通过“指针”将一组零散的内存块串联起来使用,所以如果我们申请的是 100MB 大小的链表,根本不会有问题。
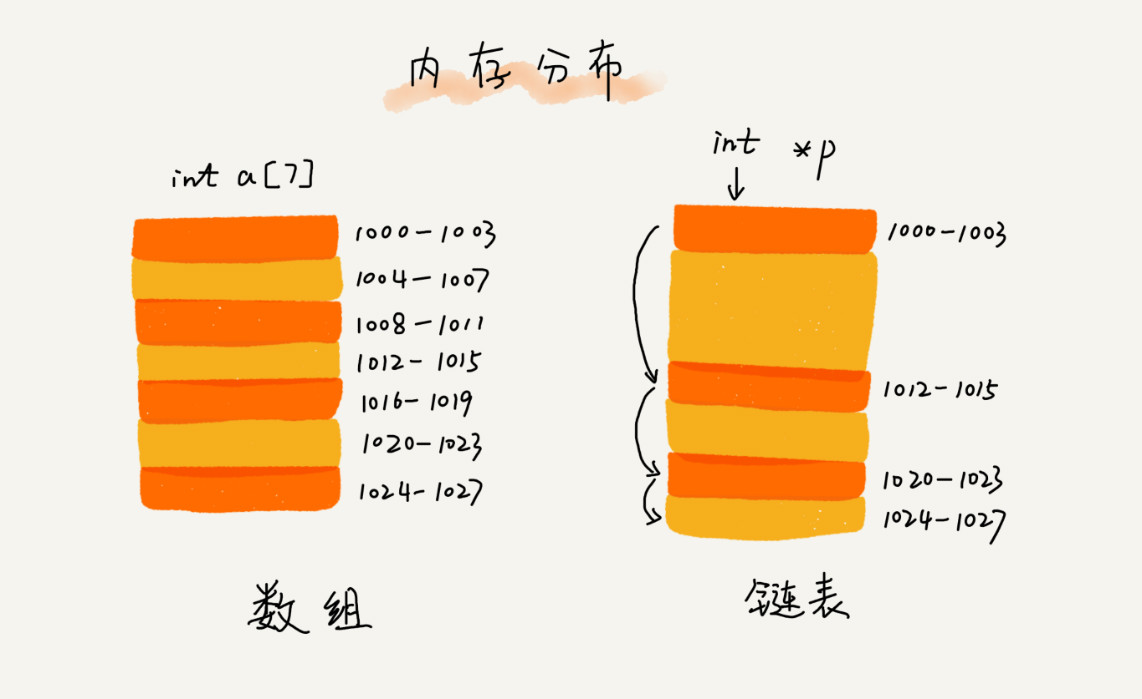
连续存储(数组)
数组具有索引,可以根据首个数据的内存地址和每个数据占得长度,直接查询到索引对应的存储位置
数组的优缺点:
优点:
存取速度快
缺点:
事先需要知道数组的长度
需要大块的连续内存
插入删除非常慢,效率低
离散存储(链表)
定义:
- n个节点离散分配
- 彼此通过指针相连
- 每个节点只有一个前驱节点,每个节点只有一个后续节点
- 首节点没有前驱节点,尾节点没有后续节点
优点:
- 空间没有限制,插入删除元素很快
缺点:
- 查询比较慢
专业术语:
- 首节点:第一个有效节点
- 尾节点:最后一个有效节点
- 头节点:第一个有效节点之前的那个节点,头结点不存储任何数据
- 头指针:指向头结点的指针变量
- 尾指针:指向尾节点的指针变量
链表的分类:
- 单链表
- 双链表 每个节点有两个指针域
- 循环链表 能通过任何一个节点找到其他所有的节点
- 非循环链表
对链表的操作:
- 增加
- 删除
- 修改
- 查找
- 总长度
单链表

class Hero: def __init__(self, name=None, no=None, nickname=None, pNext=None): self.name = name self.no = no self.nickname = nickname self.pNext = pNext def add(head, pnew): cur = head # 直接添加到尾部 # while cur.pNext != None: # cur = cur.pNext # # 此时跳出循环,将新的英雄赋给pNext # cur.pNext = pnew # 指定位置进行添加 while cur.pNext != None: if cur.pNext.no > pnew.no: break cur = cur.pNext pnew.pNext = cur.pNext cur.pNext = pnew def delHero(head, no): cur = head while cur.pNext != None: if cur.pNext.no == no: break cur = cur.pNext else: print('没有找到元素') cur.pNext = cur.pNext.pNext def is_empty(head): if head.pNext != None: return False else: return True def length(head): cnt = 0 cur = head while cur.pNext != None: cnt = cnt + 1 cur = cur.pNext return cnt def getAll(head): cur = head while cur.pNext != None: cur = cur.pNext print('编号是:%s, 姓名是:%s, 外号:%s' % (cur.no, cur.name, cur.nickname)) head = Hero()
循环链表
约瑟夫问题
设编号为1,2,… n的n个人围坐一圈,约定编号为k(1<=k<=n)的人从1开始报数,数到m 的那个人出列,它的下一位又从1开始报数,数到m的那个人又出列,依次类推,直到所有人出列为止,由此产生一个出队编号的序列

class Child(object): first = None def __init__(self, data=None, pNext=None): self.data = data self.pNext = pNext def add(self, num): cur = None for i in range(num): child = Child(i + 1) if i == 0: self.first = child self.first.pNext = self.first cur = self.first else: cur.pNext = child child.pNext = self.first cur = cur.pNext def showAll(self): cur = self.first while cur.pNext != self.first: print('小孩的编号是:%s' % cur.data) cur = cur.pNext print('小孩的编号是:%s' % cur.data) def countChild(self, m, k): tail = self.first while tail.pNext != self.first: tail = tail.pNext # 退出循环的话,已经到了最后一个小朋友 for i in range(k - 1): self.first = self.first.pNext tail = tail.pNext # 数两下,相当于tail和first分别移动一下 # 数三下, 相当于tail和first分别移动2下 while tail != self.first: # 退出循环的时候, 圈子里面只剩一个人 for i in range(m - 1): self.first = self.first.pNext tail = tail.pNext self.first = self.first.pNext tail.pNext = self.first print('留在圈子里面的小孩编号:%s' % tail.data) child = Child() child.add(1000) child.showAll() child.countChild(1000, 300) # 设置tail原因:用来判断循环列表中是否只剩一个值。
栈
栈的定义
一种可以实现“先进后出”的存储结构
栈的分类
- 静态栈
– 静态栈的核心是数组,类似于一个连续内存的数组 - 动态栈
– 动态栈的核心是链表
栈的算法
- 初始化
- 压栈
- 出栈
- 判空
- 遍历
- 清空

class Stack(object): def __init__(self): self.pTop = None self.pBottom = None def push(self, new): new.pNext = self.pTop self.pTop = new def pop(self): if not self.is_empty: self.pTop = self.pTop.pNext else: print('is none') def getAll(self): cur = self.pTop while cur != self.pBottom: print(cur.data) cur = cur.pNext def is_empty(self): if self.pTop == self.pBottom: return True else: return False def clear(self): if self.is_empty(self): return None p = self.pTop q = None while p != self.pBottom: q = p.pNext del p p = q else: self.pBottom = self.pTop class Node(object): def __init__(self, data=None, pNext = None): self.data = data self.pNext = pNext head = Node() s = Stack() s.pTop = s.pBottom = head
栈的应用
- 函数的调用
- 浏览器的前进与后退
- 表达式的求值
- 内存分配
- 走迷宫
队列
队列的定义
一种可以实现“先进先出”的存储结构
队列算法

class Node: def __init__(self, value): self.data = value self.next = None class Queue: def __init__(self): self.front = Node(None) self.rear = self.front def enQueue(self, element): n = Node(element) self.rear.next = n self.rear = n def deQueue(self): if self.empty(): print('队空') return temp = self.front.next self.front = self.front.next if self.rear == temp: self.rear = self.front del temp def getHead(self): if self.empty(): print('队空') return return self.front.next.data def empty(self): return self.rear == self.front def printQueue(self): cur = self.front.next while cur != None: print(cur.data) cur = cur.next def length(self): cur = self.front.next count = 0 while cur != None: count += 1 cur = cur.next return count
队列的应用
- 所有和时间有关的操作都和队列有关
树
树的定义
- 树有且仅有一个根节点
- 有若干个互不相交的子树,这些子树本身也是一颗树
树的专业术语
- 节点
- 父节点
- 子节点
- 子孙
- 堂兄弟
- 兄弟
- 深度
– 从根节点到最底层节点的层数被称为深度,根节点是第一层 - 叶子节点
– 没有子节点的节点 - 度
– 子节点的个数
树的分类
- 一般树
– 任意一个节点的子节点的个数不受限制 - 二叉树
– 定义:任意一个节点的子节点个数最多是两个,且子节点的位置不可改变
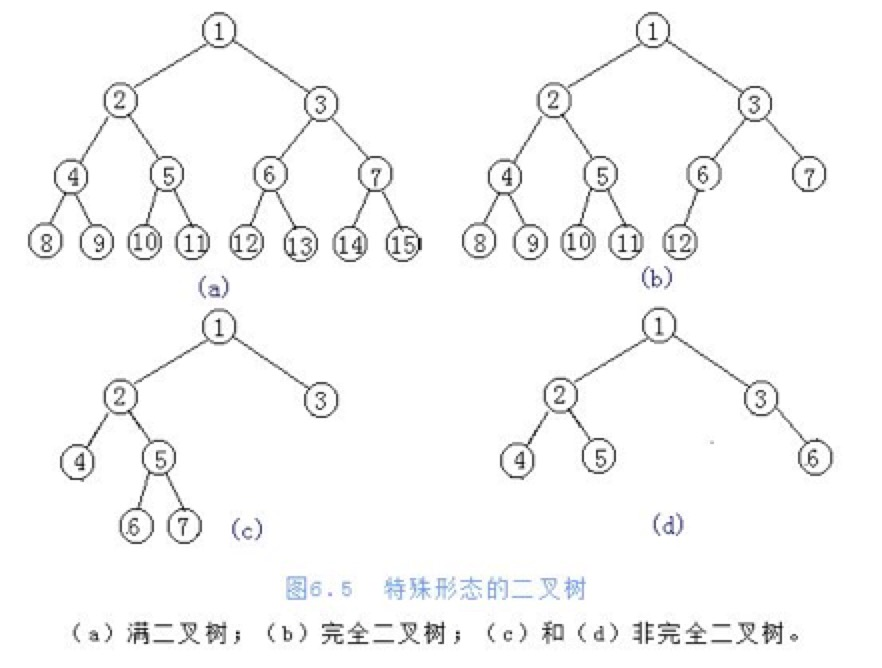
— 满二叉树:在不增加层数的前提下,无法再多添加一个节点的二叉树
— 完全二叉树:只是删除了满二叉树最底层最右边连续的若干个节点
— 一般二叉树
-森林
– n个互不相交的树的集合
二叉树的遍历方法
1.二叉树的先序遍历[先访问根节点]
- 先访问根节点
- 再先序遍历左子树
- 再先序遍历右子树
2.二叉树的中序遍历 [中间访问根节点]
- 先中序遍历左子树
- 再访问根节点
- 再中序遍历右子树
3.二叉树的后序遍历[最后访问根节点]
- 先后序遍历左子树
- 再后序遍历右子树
- 再访问根节点
#### 例一
先序:ABCDEFGH
中序:BDCEAFHG
求后序?
,,,,,
后序:DECBHGFA
#### 例二
中序:BDCEAFHG
后序:DECBHGFA
求先序?
先序:ABCDEFGH

class Node(object): """节点类""" def __init__(self, elem=-1, lchild=None, rchild=None): self.elem = elem self.lchild = lchild self.rchild = rchild class Tree(object): """树类""" def __init__(self): self.root = Node() self.myli = [] def add(self, elem): """为树添加节点""" node = Node(elem) if self.root.elem == -1: # 如果树是空的,则对根节点赋值 self.root = node self.myli.append(self.root) else: treeNode = self.myli[0] # 此结点的子树还没有齐。 if treeNode.lchild == None: treeNode.lchild = node self.myli.append(treeNode.lchild) else: treeNode.rchild = node self.myli.append(treeNode.rchild) self.myli.pop(0) def front_digui(self, root): """利用递归实现树的先序遍历""" if root == None: return print(root.elem) self.front_digui(root.lchild) self.front_digui(root.rchild) def middle_digui(self, root): """利用递归实现树的中序遍历""" if root == None: return self.middle_digui(root.lchild) print(root.elem) self.middle_digui(root.rchild) def later_digui(self, root): """利用递归实现树的后序遍历""" if root == None: return self.later_digui(root.lchild) self.later_digui(root.rchild) print(root.elem)
树的应用
- 树是数据库中数据组织的一种重要形式
- 操作系统父子进程的关系本身就是一棵树
- 面向对象语言中类的继承关系




 浙公网安备 33010602011771号
浙公网安备 33010602011771号