图解机器学习读书笔记-CH5

稀疏学习

带约束的LS+交叉验证组合是非常有效的回归方法, 缺点是参数太多时求解耗时.

稀疏学习将大部分参数置0, 大大加速参数求解.

L1约束的LS

稀疏学习使用L1条件约束:
其中,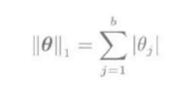

L1和L2对比:

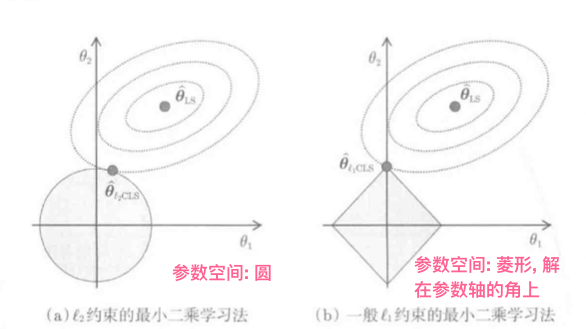
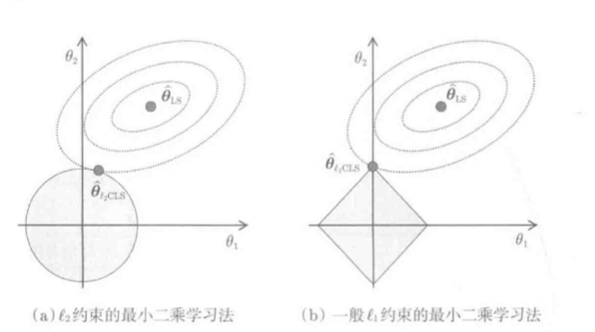
以对于参数的线性模型为例对上图做分析:

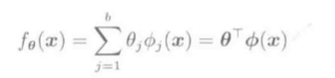
• 训练误差\(J_{LS}\)是关于\(\theta\)的向下的二次凸函数, 因此\(J_{LS}\)在参数空间内有椭圆状等高线, 底部是最小二乘解\(\hat \theta_{LS}\)
• \(\hat \theta_{L_2CLS}\):椭圆等高线和圆周交点是L2约束LS的解\(\hat \theta_{LS}\), 即\(L_2\)-Constrained Least Squares
• \(\hat \theta_{L_1CLS}\):椭圆等高线和菱形的角的焦点是L1约束LS的解\(\hat \theta\), L1约束LS的解一定位于参数的轴上

L1CLS的解在参数轴上, 很容易用稀疏的方式求解.

L1约束的LS求解

利用拉格朗日对偶问题求解, 考虑L1正则化的最优化问题:

\[\underset{\theta}{min}J(\theta), J(\theta) = J_{LS}(\theta) + \lambda\|\theta\|_1 \]

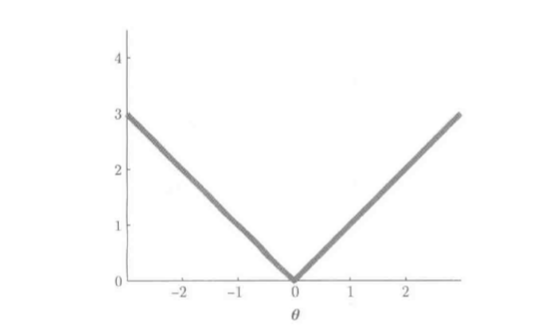
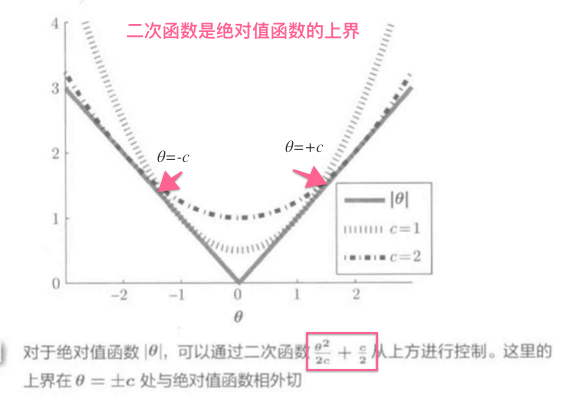
L1范数原点不能微分, 用微分的二次函数控制:

\[|\theta_j| <= \frac{\theta_j^2}{2c_j}+\frac{c_j}{2}, \forall c_j > 0 \]

函数如图:

L2正则化LS一般表达式:

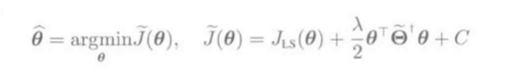
线性模型\(f_\theta(\vec x) = \vec \theta^T\phi(\vec x)\)求\(\hat \theta\):

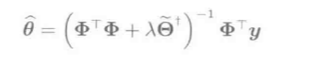
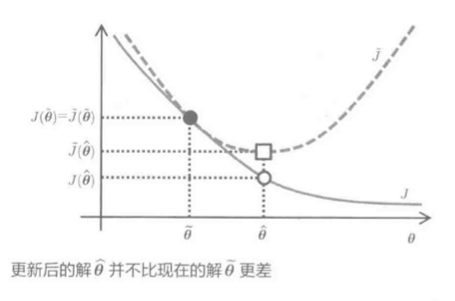
几个解的函数图像:

高斯核模型

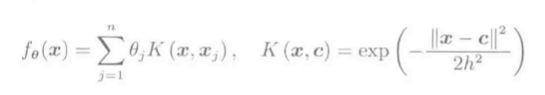
分别用L1,L2约束求解:

求解结果:

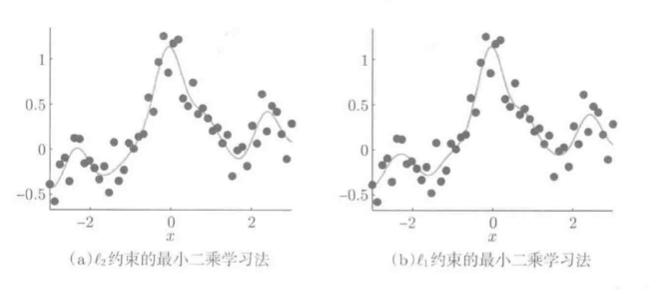
结论: 结果无太大差异, 但L2约束的LS的50个参数全部非0; L1约束LS的50个参数, 有37个为0, 学习结果是是13个核函数的线性拟合.

Lp约束的LS

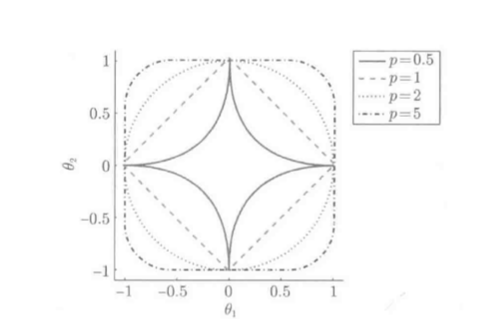
L1,L2范数的更广义定义, \(L_p\)范数:

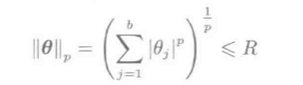
\(p=\infty\)时称最大值范数:

\(p=0时L_0\)范数表示非零向量元素个数:

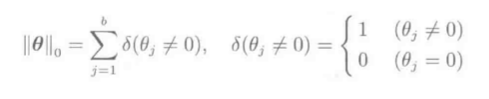
\(L_p\)范数的单位球(R=1):

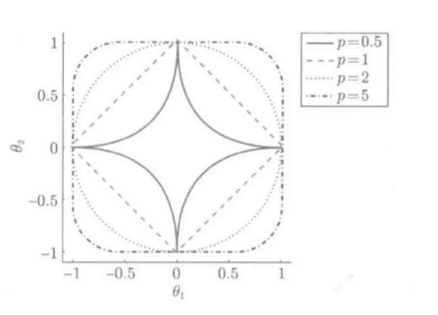
分析:

\[\begin{cases} p \leq 1& 坐标轴上呈现有峰值的尖形 \\ p \geq 1& 凸形 \end{cases} \]

稀疏解存在的特殊条件:

\[\begin{cases} 1.约束空间为凸形(非凸优化困难)\\ 2.坐标轴上呈现有峰值的尖形 \end{cases} \]

如此, 只有\(L_1\)范数满足条件, L1约束的LS是非常特殊的学习方法

满足\(L_p\)范数约束条件的空间性质:

L1+L2约束的LS

\(L1+L2\)约束的LS也称为弹性网络

先回顾两个模型.

1. 线性模型
   
   
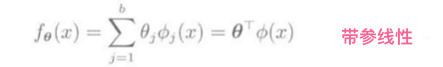
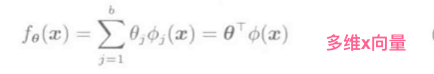
   \(\phi_j(x)\)是基函数向量, 基函数举例:
   
   

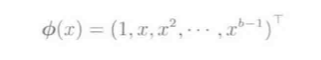
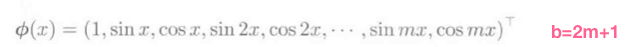
2. 核模型
   
   高斯核函数:
   

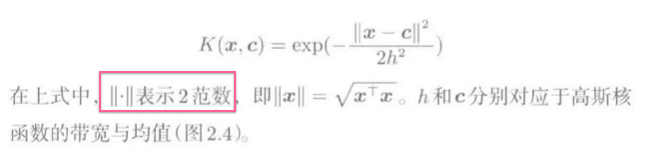
回顾\(L_1和L_2\)约束:

1. \(L_2\)约束
   
   转化为拉格朗日对偶问题:
   
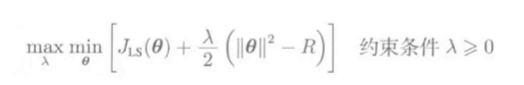
   不考虑参数空间圆的半径R时化简为:
   

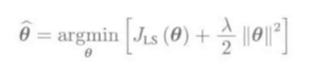
2. \(L_1\)约束:
   
   转化为拉格朗日对偶问题:
   

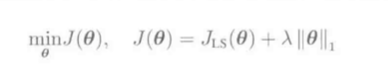
3. \(L_1和L_2\)的参数空间:
   

L1约束的限制:

1. 参数b比训练样本n多时, 线性模型可选择的最大特征数被局限为n
2. 线性模型中形成集群构造(有多个基函数相似的集合)时, \(L_1\)LS选择一个忽略其它, 核模型输入样本是簇构造是更易形成集群构造
3. 参数b比样本n少时, \(L_1\)的通用性比\(L_2\)更差

解决方案是\(L_1+L_2\):

\(L_p\)范数单位球:

\(\tau=1/2时, L_1+L_2\)范数的单位球:

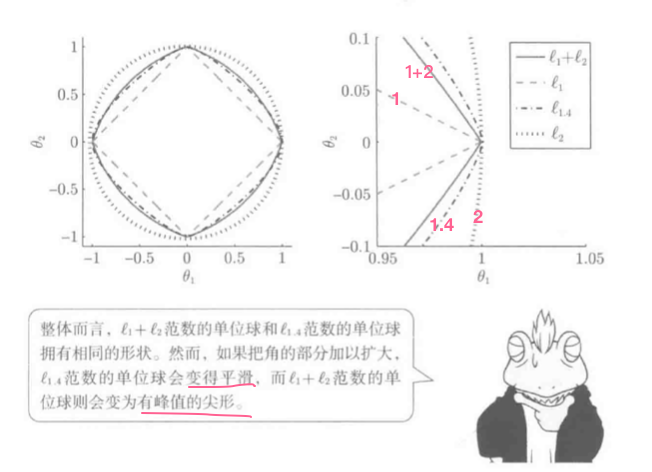
结论:

1. \(L_1+L_2\)单位球凸, 角部呈尖形, 故和\(L_1\)一样易求得稀疏解
2. 可学得n个以上非零参数
3. 基函数为集合构造时, 常以集合为单位对基函数选择
4. 比\(L_1\)约束的LS具有更高的精度