图解机器学习读书笔记-CH4
带约束条件的最小二乘法
单纯的最小二乘法容易过拟合, 带约束的最小二乘法能控制模型复杂度, 降低过拟合.
1. 部分空间约束的LS
含参线性模型, 使用全体参数空间:
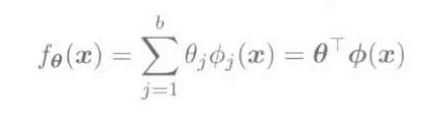
将参数空间限制在一定范围内, 防止过拟合:
P是\(bxb\)维矩阵,是P的值域\(R(P)\)的正交投影矩阵
部分空间约束的最小二乘法解\(\hat \theta\)通过将设计矩阵\(\Phi\)置换为\(\Phi P\)求得:
下图展示了添加部分空间约束对模型的影响:
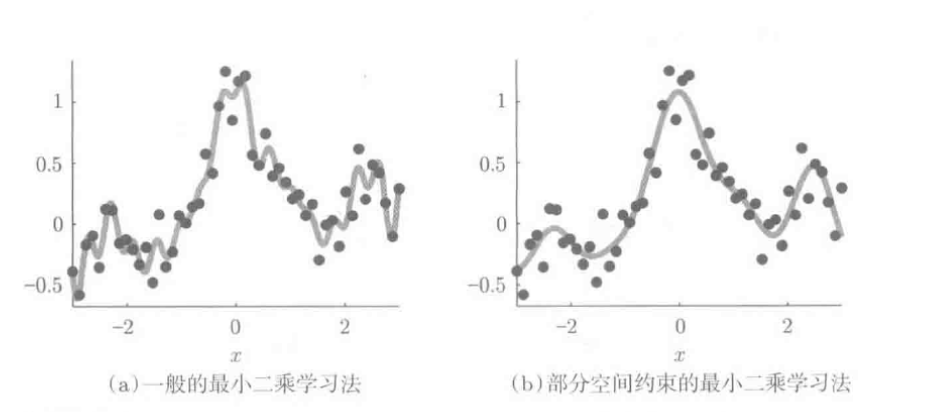
上图用三角多项式作为基函数:
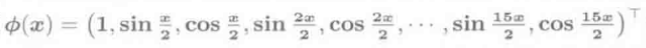图(b)添加了约束条件, 将参数限制在
的部分空间内:
2. L2约束的LS
2.1 标准L2约束的LS
部分空间约束的LS(最小二乘法), 正交投影矩阵P的设置自由度高, 操作难度大, 基于L2约束的LS相对较容易.
约束条件如下:
L2参数空间:
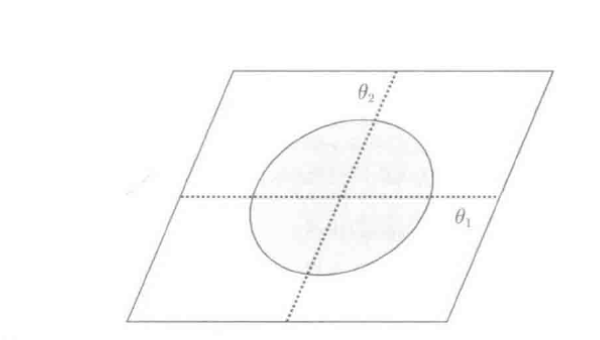
如图, 是一个参数空间原点为圆心,R为半径内的圆(一般为超球)
2.2 拉格朗日对偶问题
引入拉格朗日对偶问题:
利用拉格朗日对偶问题, 求解:
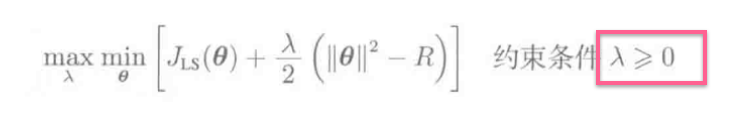
的最优解问题, 可得到最优化问题\(\underset{\theta}{min}J_{LS}(\theta)\)的解.
上式中拉格朗日待定因子\(\lambda\)的解由圆半径R决定
简化版(不由R决定\(\lambda\)):
上式\(J_{LS}(\theta)\)表示对样本拟合程度, 与\(\frac{\lambda}{2}\|\theta\|^2\)组合得到最小是, 防止过拟合
上式令关于\(\theta\)的导数为0, L2约束的LS的解\(\theta\)可通过下式求解:
上式结论:
- 将矩阵\(\Phi^T\Phi和\lambda I\)相加提高其正则性, 进而更稳定地进行逆矩阵求解.
- L2约束的LS也成为L2正则化的LS, \(\|\theta\|^2\)称为正则项, \(\lambda\)为正则化参数
- L2正则化有时也称岭回归
将设计矩阵\(\Phi\)做奇异值分解:
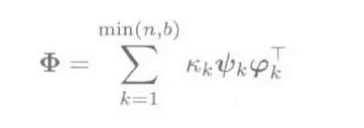
带入上上式, 则L2约束的LS解\(\hat \theta\)表示为:
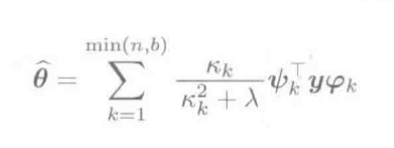
上式结论:
- \(\lambda=0\)时, L2约束的LS蜕化为一般的LS
- 设计矩阵\(\Phi\)计算条件恶劣,包含极小的奇异值\(K_k\)时, \(K_k/K_k^2=1/K_k\)变得极大, 训练输出\(\vec y\)噪声会增加
- 分母\(K_k^2\)中加入正的常数\(\lambda\), 避免\(K_k/(K_k^2+\lambda\)过大, 进而可防止过拟合
2.3高斯核模型的L2约束优化
高斯核模型
L2约束优化
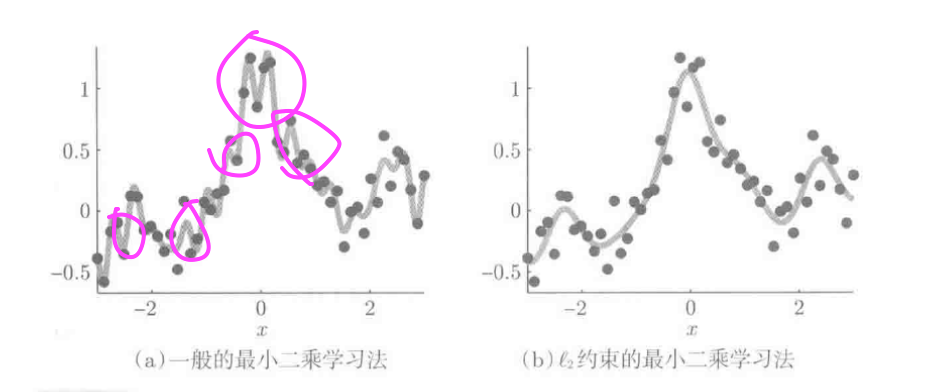
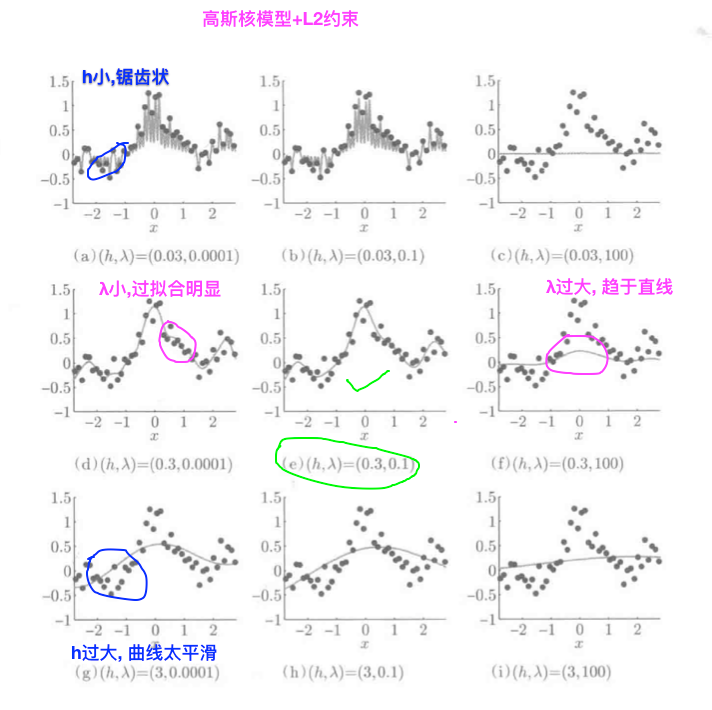
\(带宽h=0.3, 正则化参数\lambda=0.1\), 加入正则化项, 很好地抑制了过拟合.
根据标准高斯分布的函数图, 我们对比可以看出图中标红位置出现了过拟合.
2.4 更一般L2约束的LS
(1) 标准L2约束的LS
- 问题表示:
- \(\hat \theta\)求解:
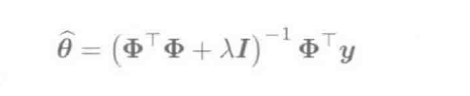
(2)更一般的L2约束的LS
使用\(bxb\)正则化矩阵G, 可得到更一般的表示:
- 问题表示:
- \(\hat \theta\)求解:
更一般的L2约束的LS解\(\theta\)求解过程, 和标准L2约束的LS大体相同:
- 参数空间:
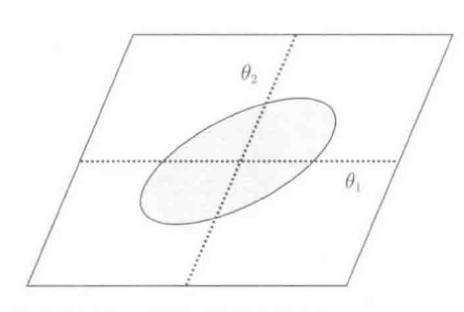
矩阵G对称正定时, $\theta^TG\theta \leq R $将数据限制在椭圆区域内. 下图为更一般的L2约束的LS参数空间:
模型选择
- 部分空间约束或L2约束的LS, 都过分依赖正交投影矩阵P和 正则化参数λ的选择
- 选择合适的P和λ至关重要
采用不同的输入样本, 决定算法中各个参数值的过程称为模型选择
下图展示一个高斯核模型+L2约束的LS中, 带宽\(h\)和正则化参数\(\lambda\)的变化对学习结果的影响:
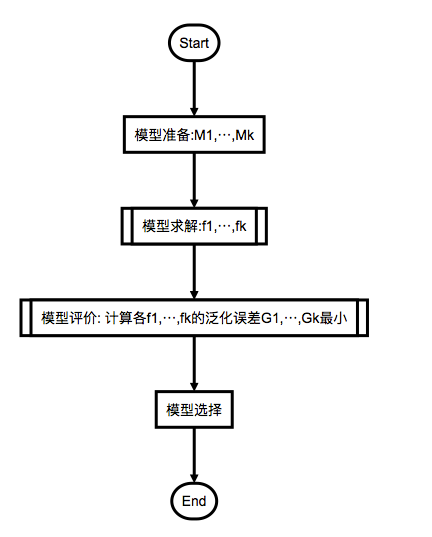
模型选择流程:
实际应用中常用交叉验证法, 拿出一部分训练样本做测试, 不参与学习, 值评价最终学习结果的泛化误差
交叉验证法流程:
K折交叉验证:
训练集分割为k个集合, 需进行k次学习, 由于各学习过程相互独立, 可以并行计算.
留一交叉验证:
设有n个样本, 每次留下一个样本做测试集, 其余n-1个训练, 共需要训练n次, 测试n次
计算繁琐, 样本利用率高, 适合小样本学习
