Exploiting Noise as a Resource for Computation and Learning in Spiking Neural Networks

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

https://arxiv.org/abs/2305.16044

 

Summary

　　脉冲神经网络支撑着大脑非凡的信息处理能力，并已成为神经形态智能的支柱模型。尽管对脉冲神经网络(SNN)进行了广泛的研究，但大多数都是建立在确定性模型上的。将噪声集成到SNN中会导致生物学上更合理的神经动力学，并可能有利于模型性能。本文通过引入包含噪声神经元动力学的脉冲神经元模型，提出了噪声脉冲神经网络(NSNN)和噪声驱动学习规则(NDL)。我们的方法展示了噪声如何作为计算和学习的资源，并从理论上为通用SNN提供了一个框架。通过结合各种SNN架构和算法，我们表明，与确定性SNN相比，我们的方法表现出有竞争力的性能，并提高了对具有挑战性的扰动的鲁棒性。此外，我们还证明了NSNN模型在神经编码研究中的实用性。总的来说，NSNN为机器学习从业者和计算神经科学研究人员提供了一个强大、灵活且易于使用的工具。

 

Keywords

脉冲神经网络，噪声脉冲神经网络、替代梯度、噪声驱动学习、神经形态智能、神经编码

 

Introduction

　　脉冲神经网络(SNN)被认为有望弥合人工神经网络和生物神经网络之间的差距。它们已被广泛用作神经科学研究中的计算模型^1,2。得益于深度学习的最新进展^3-5，SNN在计算机视觉和机器人等各种应用中也取得了显著优势^6-15。通常，大多数脉冲神经模型是由确定性神经网络(DSNN)建立的，它们忽略了脉冲神经元固有的随机性。具有噪声扰动动力学的脉冲神经元被认为更具生物学合理性，因为离子通道波动和突触传递随机性会导致噪声亚阈值膜电压^16-23。此外，它通过促进更容错的表征空间^24-26和防止过拟合²⁷，在泛化性能方面带来了潜在的好处。然而，需要一种通用且灵活的方法来充分利用噪声脉冲神经元模型，并理解噪声在脉冲神经网络中的作用。

　　先前的文献^28,29已经通过在膜电压的微分方程中包括噪声项来研究具有随机活动的脉冲神经元。这种噪声项通常被建模为在具有扩散过程的随机微分方程中导出的白色或彩色噪声^30,31。这些方法引入了具有噪声膜动力学的详细脉冲模型；然而，他们并不试图在网络级别上构建通用方法。一些研究^32-35提出了可以进行概率推理的噪声脉冲神经元的小型网络。然而，由于缺乏有效的学习方法，这些方法很难结合任意的网络架构。最近的一项研究³⁶引入了确定性脉冲响应模型(Spike Response Model)的广义线性模型变体，但他们的方法也不适用于本文感兴趣的深度SNN。在深度SNN中，一种称为替代梯度学习^37-39(SGL，伪导数⁴⁰)的特殊解决方案已成为执行反向传播时最广泛用于解决不连续性的解决方案⁴¹。虽然替代梯度方法已被证明是非常有效的⁴²，但它们缺乏理论基础和合理的解释⁴³。相比之下，神经科学知情学习方法，如STDP^44-46，在理论上是有根据的，并被证明是有前景的，但在大型网络和复杂任务中很难很好地工作。因此，人们期望开发一种有效且可扩展的学习方法，如SGL，同时保留有关STDP等学习机制的见解。

　　先前缺乏噪声脉冲神经模型的通用计算和学习协同设计限制了它们的使用。这使我们无法充分利用噪声脉冲神经网络作为机器学习模型的性能，也无法探索其作为神经科学计算工具的潜力。因此，本文旨在提供深度SNN和噪声脉冲神经模型的通用且灵活的集成。通过这种方式，我们可以使脉冲神经模型在生物学上更合理，并获得潜在的性能增益，同时能够直接受益于快速增长的深度学习领域中出现的工程进步。此外，就理论价值而言，这也证明了噪声如何在脉冲神经元的一般网络中充当计算和学习的资源⁴⁷。

　　在这里，我们展示了一个使用噪声驱动学习(NDL)范式的噪声脉冲神经网络模型(NSNN)。这里公开的方法提供了噪声脉冲神经模型和深度SNN的通用且灵活的集成。此外，NDL包含SGL，并为后者提供了深刻的解释。通过结合各种SNN架构和算法，我们展示了NSNN的有效性。此外，当面临具有挑战性的扰动(如对抗攻击)时，NSNN显著提高了鲁棒性。此外，通过基于NSNN的神经编码分析，我们展示了NSNN模型作为神经科学研究有用计算工具的潜力。

 

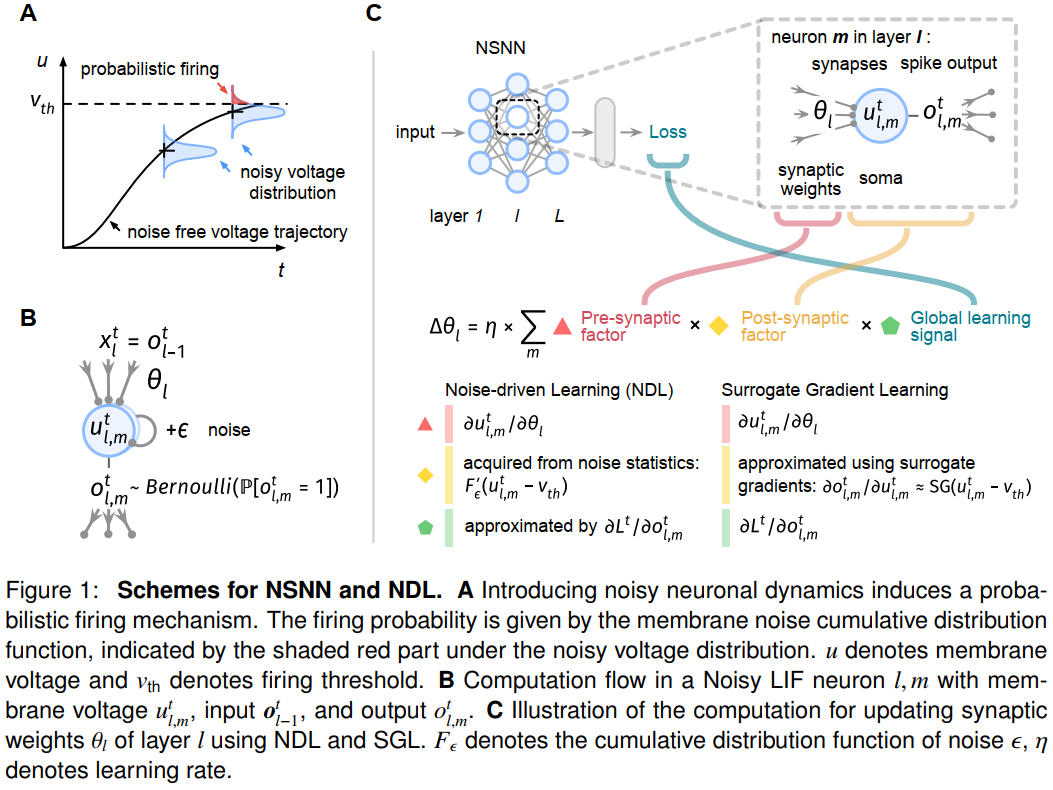
Results

Noisy spiking neural network and noise-driven learning

　　在这篇文章中，我们考虑了一种噪声泄漏积分和发放(LIF)脉冲神经元模型(见实验过程方法详细信息)，遵循了先前使用扩散近似的文献^30,31,48。它考虑了一个离散的亚阈值公式，其形式为：

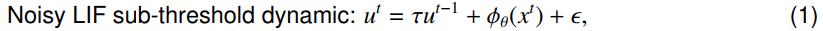
其中，u表示膜电压，x^t表示时间 t 的输入，τ是膜时间常数，而Φ_θ是参数化输入变换。噪声ε是从零均值高斯分布中得出的。引入内部噪声会导致概率发放机制(如图1A所示)，其中差值u − v_th决定发放率^21,30,31：

其中o^t是脉冲状态，P[o^t = 1] = F_ε(u^t − v_th)，F_ε是噪声的累积分布函数，v_th是发放阈值。

　　通过使用噪声LIF神经元，NSNN提出了一种通用形式的脉冲神经网络。例如，如果噪声方差Var[ε]接近零，则发放概率函数F_ε收敛于Heaviside阶跃函数，因此，噪声LIF模型包含确定性LIF情况。这表明，传统的DSNN可以被视为一种特殊类型的噪声脉冲神经网络。此外，通过考虑逻辑膜噪声，噪声LIF神经元覆盖了sigmoid神经元模型⁴⁷。

　　然后，我们通过梯度下降为脉冲神经网络提供了一个定义明确的突触优化解决方案。作为二值变量的噪声神经元编码，我们可以使用贝叶斯网络^49,50来表示NSNN，贝叶斯网络是一种概率图形模型，通过有向图来表示一组变量及其条件依赖关系。利用贝叶斯网络公式，我们可以简洁地表示NSNN中的脉冲状态。这使我们能够将突触优化期间的梯度计算转换为概率模型中的梯度估计，从而避免了有问题的发放函数导数。由此产生的噪声驱动学习(NDL)规则(见实验程序方法详细信息)如图1C所示。特别是，NDL的简洁形式使其易于与其他在线^40,51或本地学习⁵²策略相结合，以更有效地利用计算资源并处理更多样的任务。

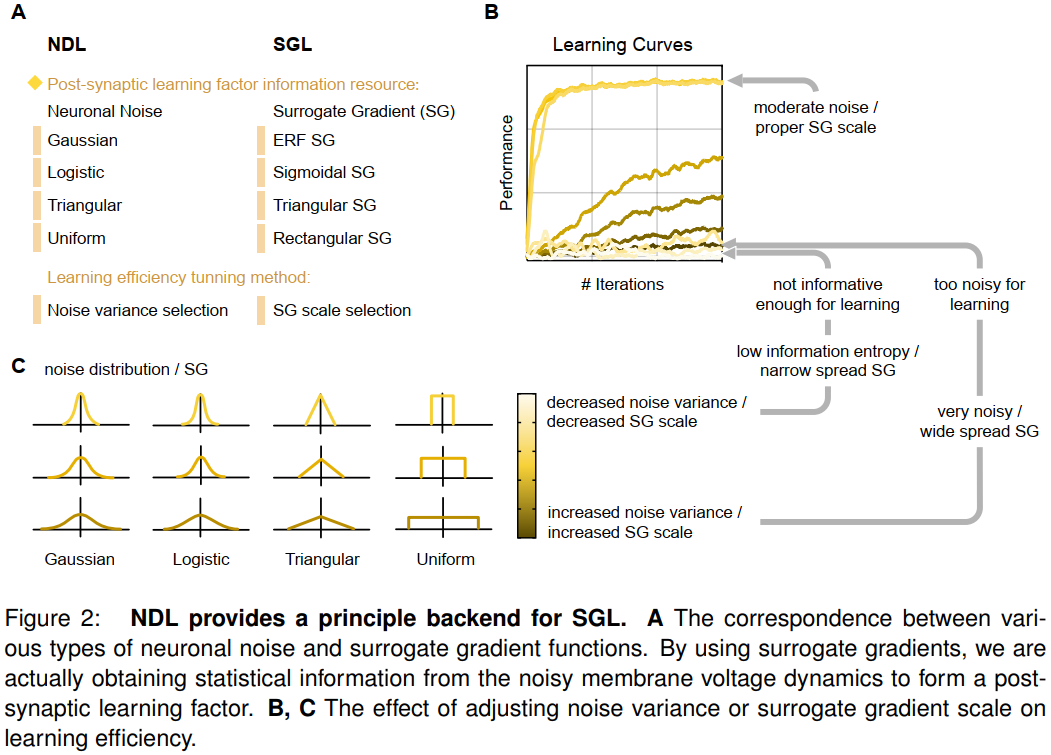
　　NDL的一个值得注意的特点是为SGL提供了原则性的理由。通过利用三因素学习规则框架^53,54，我们展示了图1C中所示的数学关系，表明SGL可以被视为一种特殊类型的NDL。尽管在二值网络中，替代梯度^7,37,38,42通常与直通估计器^55-58相关，但从脉冲神经元的角度来看，这种关联并不合理。从这个意义上说，SGL似乎是一种特别的解决方案，而不是一种有原则的学习方法^37,43。NDL揭示了替代梯度的本质，即从神经元膜噪声统计中获得突触后学习因子。图2A说明了NDL中的噪声方差选择和SGL中的替代梯度尺度选择之间的关系。当噪声方差很小时，NSNN的概率推理前向可以通过DSNN中的确定前向传播来近似。因此，在NSNN框架内派生的NDL包含了传统DSNN中的SGL。这也提供了用于调整SGL中替代梯度函数的尺度(形状)的随机噪声解释。图2B和2C显示了这种方差选择或尺度选择过程对脉冲神经网络学习效果的影响，表明调整SGL中替代梯度函数的尺度可以被视为选择NDL中具有不同方差的噪声。

 

NSNN leads to high-performance spiking neural models

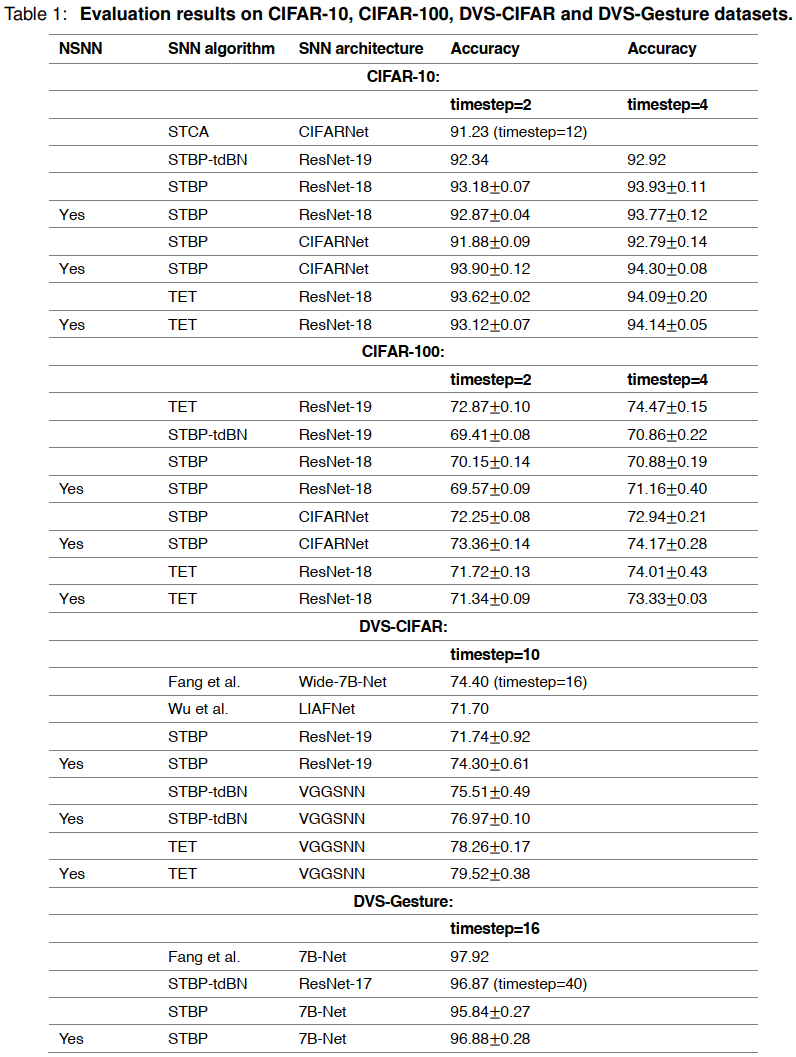
　　为了验证神经网络的有效性和兼容性，我们使用神经网络架构和算法的各种组合在多个识别基准数据集上进行了实验。我们考虑的识别数据集包括静态图像数据集，包括CIFAR-10和CIFAR-100⁵⁹，以及使用DVS相机(硅视网膜)收集的事件流数据集，其中包括DVS-CIFAR⁶⁰和DVS-Gesture⁶¹。更多实验细节见实验程序实验细节。

　　我们在这些数据集上分析了模型的精度，这里我们主要关注与SNN模型的比较。如表1所示，CIFAR-10和CIFAR-100的结果证明了NSNN在静态图像识别任务中的有效性。例如，在CIFAR-10上，NSNN模型(带有STBP, CIFARNet)在两个模拟时间步骤内实现了0.9390的精度，而其精度对应模型报告了0.9188。我们的结果表明，NSNN与各种SNN架构和算法都能很好地协同工作，表现出了很好的兼容性。因此，NSNN可以受益于更高效的SNN算法或架构。例如，当使用ResNet-18架构时，使用更高效的TET算法的NSNN模型的性能明显优于使用STBP的NSNN模式(表1，CIFAR-10，CIFAR-100)。NSNN在事件流数据识别任务上也表现出了有效性和兼容性(表1，DVS-CIFAR，DVS-Gesture)，并优于DSNN。特别是，在DVS-CIFAR数据上，具有STBP和ResNet-19的NSNN模型显著优于其DSNN模型，其他组合的性能改进也很明显。由于样本数量有限，DSNN在处理DVS-CIFAR和DVS-Gesture数据时经常会遇到严重的过拟合。然而，在NSNN中，内部噪声提高了模型的泛化能力，使其性能优于确定性模型。NSNN中的内部噪声带来的这些泛化改进与ANN中先前的研究结果^25-27一致。

 

NSNN leads to improved robustness against challenging perturbations

　　鲁棒性对于脉冲神经模型的信息处理至关重要，以防止现实世界环境中的外部扰动和干扰。从应用的角度来看，当面临损坏的输入(可能由数据收集和处理中的误差引起)和扰动的内部信息流(可能由不同单元之间的通信异常引起)时，鲁棒性确保了可靠的性能。在构建生物学合理的计算神经回路方面，鲁棒脉冲神经模型与生物回路的噪声但有弹性的特性更加一致^20,62,63。

　　接下来，我们展示了通过使用NSNN实现的鲁棒性的改进。为此，我们对CIFAR-10、CIFAR-100和DVS-CIFAR数据进行了扰动识别实验(见实验过程实验细节)。我们通过测量DSNN和NSNN在各种类型和强度的扰动下的精度和损失值来评估它们的性能。模型按照之前的识别实验中的描述进行训练，并使用输入水平或脉冲状态级扰动进行测试。

　　我们考虑了几个具有挑战性的输入级扰动。对于静态图像数据CIFAR-10和CIFAR-100，我们使用具有挑战性的对抗攻击来构建损坏的输入。这项工作利用了两种对抗攻击：快速梯度符号法(FGSM)和直接优化法(DO)。对于事件流数据DVS-CIFAR，我们使用EventDrop⁶⁴扰动，其基本思想是随机丢弃概率为ρ的一部分事件。我们还考虑直接干扰SNN中的所有脉冲状态(脉冲神经元的发放状态)，以直接模拟生物神经回路中的脉冲序列变异性。扰动的强度由参数β控制。详细内容见实验程序。

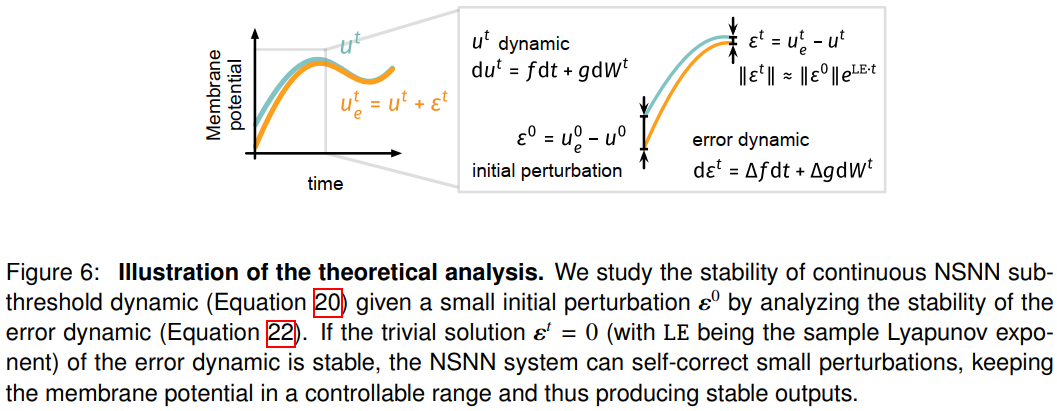
　　图3显示，使用NSNN显著提高了静态数据识别任务的鲁棒性(CIFAR-10、CIFAR-100)。当面临具有挑战性的对抗攻击和隐藏状态扰动时，NSNN模型始终优于DSNN模型。例如，在CIFAR-100 FGSM对抗攻击实验中(图3B)，NSNN表现出良好的弹性，而DSNN的可靠性随着扰动强度的增加而急剧下降。类似地，当面临神经元脉冲状态的直接干扰时(图3C)，NSNN表现出优于确定性对应的鲁棒性。对DVS-CIFAR数据的扰动实验也表明，NSNN模型比DSNN具有更好的鲁棒性(表2, 3)。在大多数情况下，当面临输入级EventDrop扰动时，NSNN比其确定性对应实现了更低的损失和更高的精度(表2)。类似地，如表3所示，当面对隐藏状态扰动时，NSNN表现出良好的弹性。它们的优越性随着扰动(脉冲状态)水平的增加而变得明显。例如，在β=0.01的扰动水平下(使用STBP和ResNet-19)，NSNN的精度比DSNN高4.5%。当扰动水平增加到0.04时，NSNN的精度领先于DSNN达到46.3%。我们在下文中对内部噪声和模型稳定性进行了理论分析(见实验程序方法细节)。

 

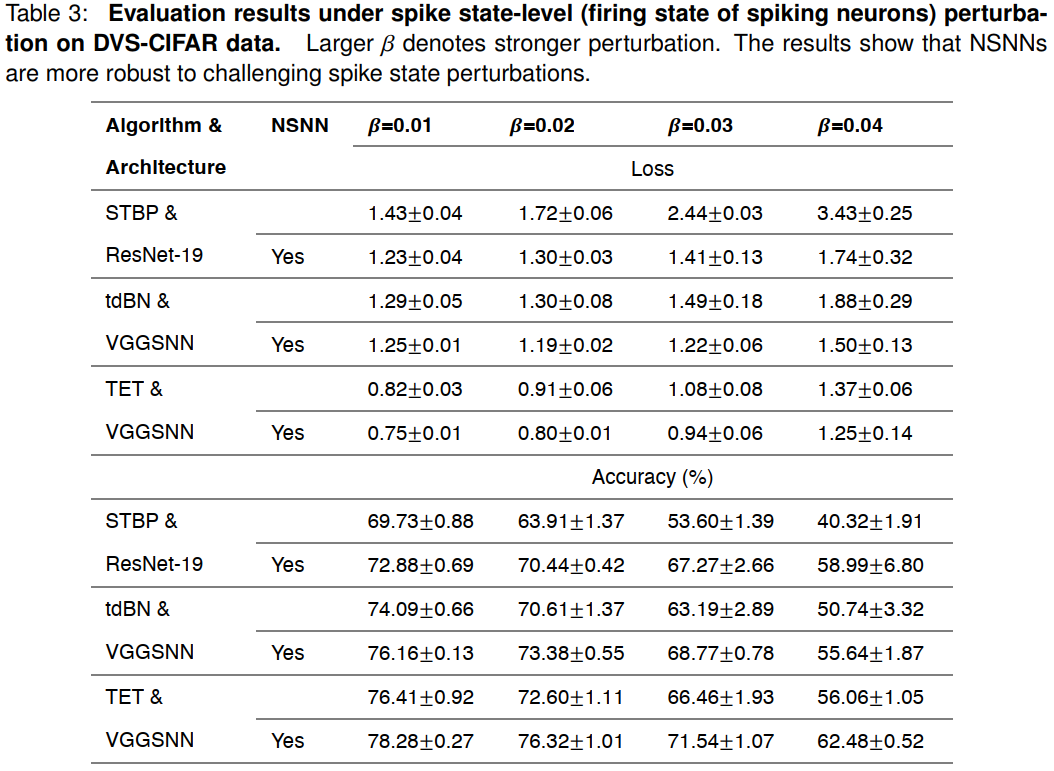
NSNN demonstrates a promising tool for neural coding research

　　尽管在神经电路中捕捉到了基于脉冲的范式，但传统的DSNN未能考虑到神经脉冲训练的可靠性和可变性^65,66，这限制了它们在神经编码研究中作为计算模型的应用。相比之下，NSNN可以忠实地恢复预测可靠性和神经脉冲序列的可变性，如图4A所示。因此，NSNN证明了一种研究神经编码的有用工具，其中为了提供有关动态感觉线索的信息，脉冲神经元的动作电位模式必须是可变的⁶⁷。

　　我们首先展示了NSNN如何用于脉冲神经模型中的神经编码分析。特别地，我们利用NSNN模型为发放率编码策略提供经验证据。具体而言，NSNN的内部随机性导致在给定相同输入的试验之间的神经编码(最终脉冲层的脉冲输出)和预测略有不同(图4A)。这允许分析神经编码发放率的变化与NSNN中最终预测的稳定性(可靠性)之间的Pearson相关性。由于我们在这里考虑识别任务，我们使用包含更多语义信息数据的最终脉冲神经元层的输出作为神经编码。我们使用Fano因子(FF)来数值测量神经编码中的发放率变化，并使用预测向量的余弦相似性来测量预测稳定性(另请参见实验程序实验细节)。较大的FF表示不同试验之间的发放率变化较大，而较高的预测余弦相似性对应于更稳定的预测输出。我们发现，在学到的NSNN中，发放率的变化与预测的稳定性之间存在显著的负相关性(图4B)。这些结果对SNN架构和算法的各种组合是鲁棒的，这表明这些NSNN学习了基于主要发放率编码的策略。这是有道理的，因为膜噪声注入在发放过程中引入了不确定性，降低了基于时间的精确脉冲编码的可靠性。由于相同的发放率(在这里用模拟步骤中的发放计数表示)可以对应于不同的脉冲序列，因此基于发放率的编码可以通过构建具有更好容错性的表征空间来提高模型的鲁棒性。

　　接下来，我们使用视网膜神经记录对自然视觉场景进行神经活动拟合⁶⁸(图4C)。我们为这个神经活动拟合任务构建了具有相同结构的DSNN和NSNN模型。这些脉冲神经模型以视觉场景为输入，以记录的视网膜反应为目标输出，并进行优化以产生类似于记录的神经活动的脉冲序列。为了将这些脉冲神经模型与当前最先进的模型进行比较，我们还考虑了有竞争力的卷积神经网络(CNN)模型^69,70作为基线。我们评估了记录和预测的神经活动之间的Pearson相关系数，以在数值上比较这些模型的性能。为了说明DSNN模型未能说明感兴趣的神经活动的可变性，我们在图4E中显示了代表性神经元的脉冲光栅和发放率。如图4E所示，DSNN模型无法再现可变的脉冲模式，也无法准确拟合真实的发放率曲线。相反，我们观察到使用NSNN有显著改善(图4D)。NSNN模型在拟合脉冲活动和发放率方面表现良好。此外，与CNN模型相比，NSNN模型可以用更少的模型参数来展示竞争性能。这些结果表明，通过将性能优化应用于生物学上合适的NSNN模型，可以构建神经编码的定量预测模型⁷¹。

 

Discussion

　　在这项研究中，我们通过利用神经元噪声作为脉冲神经网络中的计算和学习资源，报道了噪声脉冲神经模型和噪声驱动学习。我们在确定性脉冲神经元模型^28,31,72中引入了膜噪声项，制定了这些噪声脉冲神经元的网络，并推导了NDL学习方法来执行突触优化。我们在多个数据集上的结果表明，NSNN表现出有竞争力的性能和改进的泛化能力。进一步的扰动测试表明，NSNN对各种扰动(包括具有挑战性的对抗攻击)表现出了改进的鲁棒性，从而为内部噪声模型的稳定性分析提供了支持。此外，NSNN可以很容易地与各种SNN算法和网络架构集成，使我们的方法能够简单地推广到需要随机性的广泛领域。最后，我们从编码策略分析和构建预测编码模型的角度进行了讨论，并证明了神经网络为神经编码研究提供了一个很有前途的工具。

　　这项工作提出了一种构建和训练脉冲神经网络的新方法。NSNN框架能够将具有不同分布和方差的内部噪声灵活地集成到SNN模型中。在机器学习中，引入内部噪声通常会带来性能优势，例如防止过拟合和增强模型鲁棒性。因此，可以利用NSNN来获得更好的性能模型。与NDL结合的NSNN的计算和学习形式简洁明了，在DSNN实现的基础上使用简单的模块替换，可以很容易地在更大的网络架构中实现。在这里，我们证明了NSNN和NDL的组合可以很好地与代表性的网络架构和算法相结合。展望未来，NSNN可以很容易地与更大的模型集成，如脉冲Transformer^73,74。尽管我们目前在实验中使用时序反向传播沿时间维度分配信度，但NDL与潜在的在线或本地学习方法兼容。对噪声脉冲神经模型的进一步研究可以为设计局部在线学习机制^40,51,52提供见解，并将它们与NDL相结合，形成更具生物学合理性的SNN学习方法。因此，NSNN为推进脉冲神经网络及其学习方法提供了一条很有前途的途径。

　　脉冲神经模型因其基于生物学合理性的脉冲计算范式而在神经科学研究中广受欢迎。然而，传统的确定性脉冲神经模型无法解释神经脉冲序列的可变性⁶⁷。因此，对噪声脉冲神经模型的研究，旨在在计算水平上提供一个有用的工具，对计算神经科学有实际的好处。例如，NSNN可用于神经元类型^2,75，神经系统识别^76,77，以及构建神经回路的预测对应^78,79。在本文暴露的实验中，我们主要关注神经网络在神经编码中的潜在应用。这是神经科学和其他领域的热门研究课题，如计算机视觉、神经形态计算、神经假体和脑机接口。我们的结果表明，NSNN能够恢复神经电路的可靠性和可变性。值得注意的是，在将神经响应拟合到自然视觉场景的任务中，NSNN比传统的ANN模型用更少的参数获得了具有竞争力的性能。因此，NSNN为建立各种感觉神经回路的计算账户提供了一个很有前途的工具，并将使大脑中的复杂神经计算模型更加丰富。

　　总之，本研究中引入的NSNN模型在推进脉冲神经网络研究和启发人工智能算法和神经形态模型发展方面具有巨大潜力。本文采用的方法为计算神经科学研究提供了更丰富的复杂脉冲计算模型，为更好的计算工具铺平了道路。这些模型将有助于更深入地理解神经计算，并揭示神经处理机制。

 

EXPERIMENTAL PROCEDURES

Data and code availability

　　本文中使用的所有数据都是公开的，可以访问CIFAR (CIFAR-10, CIFAR-100)数据集，DVS128 Gesture (DVS-Gesture)数据集和CIFAR10-DVS (DVS-CIFAR)数据集。代码可以发现在https://github.com/genema/Noisy-Spiking-Neuron-Nets (https://doi.org/10.5281/zenodo.7986394)。

 

Method details

Notations

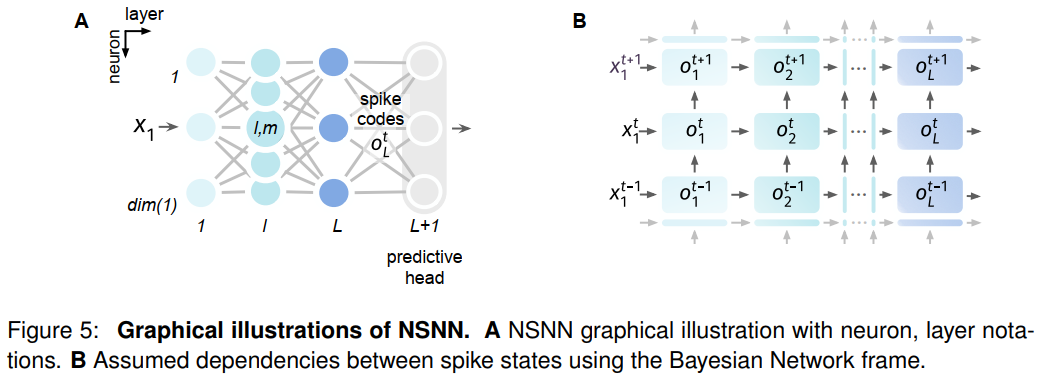
　　我们用x, u, o来表示输入、膜电位和脉冲输出。此外，表示在时间 t 的层 l (其维数为dim(l) = dim(x_l))中的神经元m的变量，其中l∈[1, L]和t∈[1, T]。我们还使用黑体字来表示变量的集合或矩阵，例如，在时间步骤 t 的第 l 层的变量被标记为。脉冲状态空间被标记为。符号, p(·)和F(·)分别是期望、概率、概率分布和累积分布函数。

 

LIF neuron

 

Noisy LIF neuron

　　这里提出的噪声LIF是基于先前使用扩散近似的工作^30,31,48，其中亚阈值动态由Ornstein-Uhlenbeck过程^83,84描述：

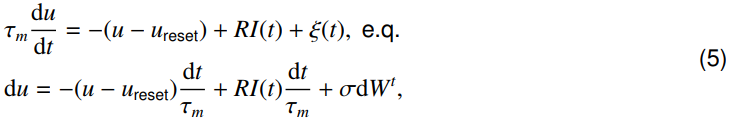
　　白噪声ξ是一个随机过程，σ是噪声的振幅，dW^t是dt中Wiener过程的增量³¹。由于σdW^t是从零均值高斯中提取的随机变量，因此该公式直接适用于离散时间模拟。具体来说，使用Euler-Maruyama方法，我们在公式4的右侧添加了一个高斯噪声项。在不失一般性的情况下，我们将离散形式的加性噪声项扩展到一般连续噪声⁸⁵，通过公式4，噪声LIF的亚阈值动态可以描述为：

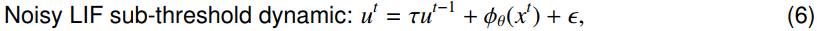
其中噪声ε独立于满足和p(ε) ＝ p(-ε)的已知分布。公式6也可以通过离散化LIF神经元^23,86的Itô随机微分方程变体来获得。在这篇文章中，我们考虑了所有噪声LIF神经元的高斯噪声。

　　由于随机噪声的注入，膜电位和脉冲输出成为随机变量。使用噪声作为介质，我们自然地获得了基于阈值发放机制的噪声LIF的发放概率分布：

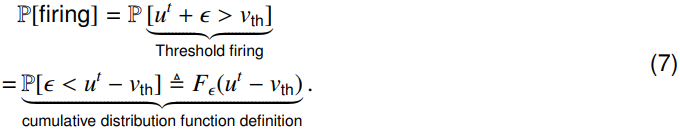
因此，

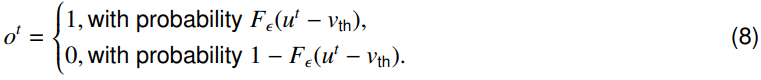
　　上面的表达式显示了噪声如何作为计算资源⁴⁷。因此，我们可以将噪声LIF的发放过程公式化为：

　　具体而言，它与先前关于逃逸噪声模型的文献^30,87,88有关，其中差u − v_th决定神经元发放概率^21,31。此外，噪声LIF采用了与LIF模型相同的重置机制。除非另有说明，否则我们在本研究中关注的是离散形式，这具有实际意义。

 

Noisy Spiking Neural Network

　　我们在这里以NSNN模型作为概率识别模型为例。设表示时间 t 的输入，使用公式6-9中的噪声LIF的动力学，由L+1层组成的NSNN由下式给出：

　　层 l 的输出是脉冲空间中的表征向量，膜电压，映射。噪声向量由具有已知分布的独立随机噪声(本文中为高斯)组成。预测头包括参数化映射和损失函数 f，表示对来自神经表征的预测进行解码并计算损失值的部分。表示映射(例如全连通或卷积)，因此关于参数θ_l可微。如上所述，将突触参数按层划分不会导致失去一般性，因为它们可以定义为任何可微映射。

　　例如，为了解决识别问题，我们将考虑预测概率模型，其中映射使用神经表征计算预测得分。函数 f 可以是预测分布和目标分布的交叉熵。注意，这里的计算瞬时损失，不同于在整个时间窗口上计算的，并忽略潜在的在线学习⁸²。

　　由于每个神经元都为一个随机变量编码，我们可以通过贝叶斯网络模型来描述NSNN，并将给定输入的所有脉冲状态的联合分布表示为：

其中层表示为。

 

Noise-driven Learning

 

Theoretical analyses on internal noise and stability

 

Experimental details

　　实验使用带有Intel I5-10400、64GB RAM和两个NVIDIA RTX 3090的工作站进行。结果报告为独立运行的平均值和标准差。

 

Details of recognition experiments

　　CIFAR数据集⁵⁹包括用于训练的50k 32×32图像和用于评估的10k图像。我们采用随机裁剪、随机水平翻转和AutoAugment⁹⁶作为训练样本。在训练和评估阶段，使用z-分数缩放对预处理的样本进行归一化。DVS-CIFAR数据集⁶⁰是一个具有挑战性的神经形态基准，通过DVS相机使用来自CIFAR-10的图像记录。我们在以前的工作⁹⁷中采用了预处理流水线，即将原始集划分为9k样本训练集和1k样本评估集，所有事件流文件都在空间上下采样到48×48。我们根据之前的研究⁹扩充了训练样本。DVS-Gesture数据集⁶¹使用DVS128事件摄像机进行记录。它包含了29名受试者在三种照明条件下的11个手势的记录。

　　我们使用数据集的观察-标签对优化了SNN模型，并计算了非重叠测试数据的性能指标。预测精度被用作这些任务的性能指标。对于每种网络架构和SNN算法组合，我们通过网格搜索为不同架构和算法组合下的DSNN和NSNN设置最优超参数，以确保公平比较。我们在结果中指出了相应的模拟时间步长，这是我们离散SNN实现的模拟持续时间。对于静态图像数据，静态图像是重复输入的，因此较长的模拟时间步长通常会导致更准确的识别。对于事件流数据集，将固定长度的连续事件流离散为模拟时间步长时间窗口。因此，更大的模拟时间步长导致更精细的计算和更准确的识别。

　　对于CIFAR-10、CIFAR-100和DVS-Gesture实验，我们将膜噪声的标准差设置为0.3；对于DVS-CIFAR实验，我们设置为0.2。这些配置在性能和弹性之间提供了一个公平的平衡。对于DSNN的SGL，我们采用ERF替代梯度。Adam解算器⁹⁸和余弦退火学习率调度器⁹⁹用于训练所有网络。我们在表4中列出了我们在识别实验中采用的超参数。初始学习率是通过网格搜索获得的。本文中使用的ResNet-19¹⁰⁰、VGGSNN⁹、CIFAR-Net⁸和7B-Net¹⁰¹ SNN架构遵循了以前工作中的原始实现。ResNet-18结构由64C3-2(64C3-4C3)-2(128C3-128C3)-2(256C3-256C3)-2(512C3-512C3)-AP-FC给出。AP表示平均池化，FC表示全连接层，C表示卷积层。这里使用的SNN算法STBP⁷、STBP-tdBN¹⁰⁰(tdBN)和TET⁹也遵循先前文献中提出的原始实现。

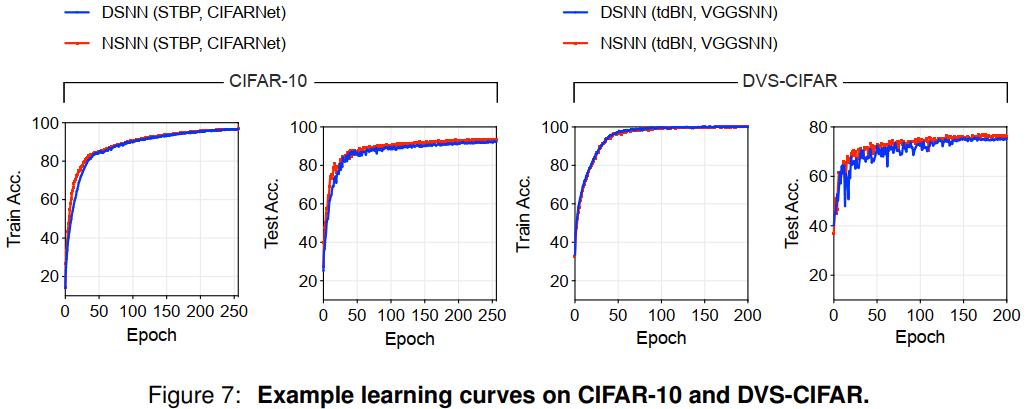
　　在这里，我们还可视化了DSNN和NSNN的代表性学习曲线。从图7中可以看出，NSNN比DSNN表现出更高的学习效率。这种优势在容易过拟合的数据集上更为明显，例如DVS-CIFAR数据。我们还注意到，与DSNN相比，使用NSNN会导致训练时间略有增加。这主要是因为噪声LIF神经元的发放过程包括计算发放概率，然后从伯努利分布中采样。这些额外的时间大部分来自采样步骤，因为我们使用的PyTorch框架没有针对随机分布的采样进行有针对性的优化。例如，在CIFAR-10数据上训练CIFARNet对于DSNN大约需要183分钟，对于NSNN大约需要194分钟。

 

Effect of internal noise level on network performance

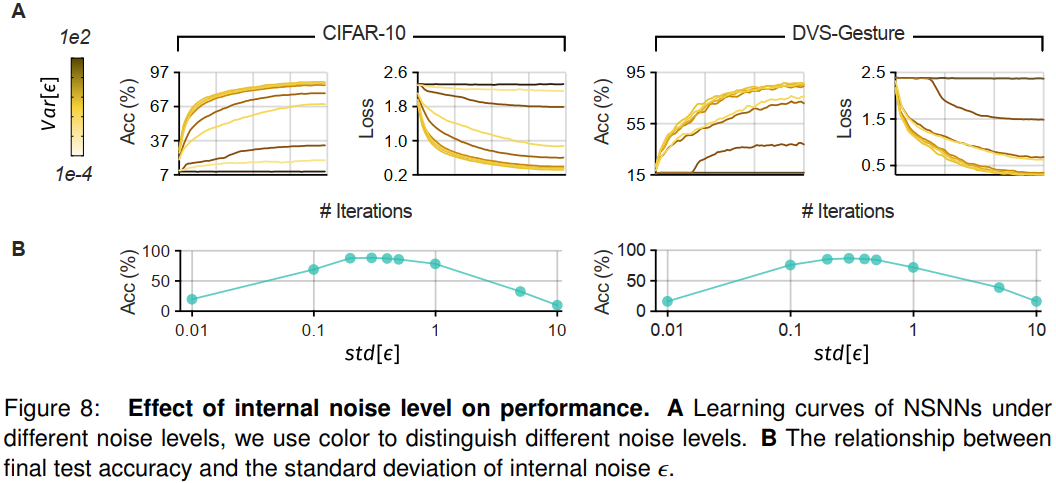
　　内部噪声水平影响学习，因为NDL中的突触后因子是使用膜噪声ε的概率密度函数计算的。当方差很小时，噪声分布收敛到信息有限的狄拉克分布(通过信息熵测量)，阻止突触后因子获得足够的信息来有效地执行学习。在推理的情况下，噪声水平直接影响发放分布的随机性。高方差噪声会扰乱网络中决定性信息的流动，导致性能大大恶化。

　　在前面的内容中，我们已经提供了关于内部噪声、网络稳定性和性能的理论解释。在这里，我们从经验上证明了温和的噪声对网络性能是有益的。我们的经验发现与先前的文献⁶²一致，文献⁶²表明一定量的噪声可以提高网络性能。我们使用CIFAR-10和DVS-Gesture数据集进行了实验，并在60个epoch内训练了具有不同内部噪声水平设置的相同网络。图8A中的学习曲线和精度-标准差曲线显示了结果。我们的观察结果表明，当内部噪声的方差从0增加时，模型的性能最初会提高，然后下降。值得注意的是，NSNN在中等值取得了高性能(参见图8B)，证实了我们的直觉，即中等噪声对高性能至关重要。根据我们的研究结果，在中等噪声范围(从0.2到0.5)内，std[ε]的变化对最终性能没有显著影响。这为我们在实践中使用NSNN时提供了一系列内部噪声级别可供选择。

 

Details of recognition experiments with perturbations

　　在这里，我们列出了实验中外部扰动的细节如下。我们将要评估的模型表示为NN。在直接优化(DO)方法中，我们通过直接求解约束优化问题来构造对抗样本：

其中∆x表示对抗扰动，x+∆x是对抗样本。它是使用PyTorch和GeoTorch¹⁰²工具包实现的。L-2范数有界加性扰动张量由零初始化，并用Adam解算器以0.002的学习率迭代30次优化。之后，使用加性扰动来产生对抗样本，并将其输入目标模型(本工作中的DSNN或NSNN)。FGSM方法的实现遵循原始实现¹⁰³，其中对抗样本构造为：

　　动态输入的输入级EventDrop⁶⁴扰动是通过在原始输入脉冲序列中随机丢弃脉冲来构建的。丢弃概率由参数ρ设定。我们考虑的丢弃策略是随机丢弃⁶⁴，它结合了空间和时间方面的事件丢弃策略。在评估过程中，我们首先对测试集中的每个样本单独执行EventDrop，然后向受试者提供受干扰的输入。

　　脉冲状态级扰动包括两种扰动：发放态从1到0(脉冲到静默)和发放态从0到1(静默到脉冲)。为了简化设置，我们使用一个参数β来控制两种变化的概率。设变量o_old表示原始脉冲状态，如果o_old = 1，我们有P[o_new = 0] = β，否则，如果o_old = 0，P[o_new = 1] = β。

 

Details of recognition task coding analyses

　　在这一部分中，我们使用了先前识别实验中学到的模型；它们的模拟时间步长分别为2、2、10和16。用于计算Pearson相关系数的测试样本的数量对于CIFAR-10、CIFAR-100、DVS-CIFAR为500，对于DVS-Gesture为200。

　　Fano因子¹⁰⁴测量脉冲计数的可变性。让我们将神经元的脉冲计数(L, m)表示为，平均值表示为。与平均值的偏差计算为，Fano因子为。

 

Details of neural activity fitting experiments

　　在神经活动拟合实验中，我们使用了适应黑暗的蝾螈视网膜的神经记录⁶⁸。原始数据集包含两个视网膜对两部电影的视网膜神经反应。我们在这个实验中只使用了一部分数据(视网膜2和电影2)。它包含了老虎狩猎的复杂自然场景，大约60秒长。电影被离散为33毫秒的桶，所有帧都被转换为灰度级，分辨率为360像素×360像素，每像素7.5µm×7.5µm，覆盖视网膜上2700µm×2700µm的区域。神经记录包含49个细胞的42次重复。我们将所有记录划分为1秒的刺激-反应样本对，并将帧下采样到90像素×90像素。数据被划分为不重叠的训练/测试(50%/50%)部分。

　　在神经活动拟合实验中，DSNN和NSNN模型的网络架构为16C25-32C11-FC64-FC64-FC64-FC49。FC表示全连接层，而C表示卷积层。这些模型是使用Adam优化器和余弦衰减学习率调度器进行训练的，从0.0003的学习率开始。小批量大小被设置为64，并且模型被训练了64个epoch。在测试时，默认情况下，测试样本的长度与训练样本的长度相同(1秒)。在训练过程中，对DSNN和NSNN模型进行优化，以最大限度地减少最大平均偏差(MMD)损失^105,106。我们使用了一阶突触后电位(PSP)核¹⁰⁷，它可以有效地描述脉冲序列数据中的时间依赖性。将预测的、记录的脉冲序列分别表示为，我们可以将PSP核MMD预测损失写成：

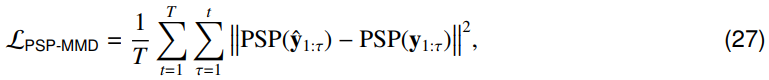
其中，我们设置时间常数τ_s=2。对于DSNN模型，我们在识别实验中使用了ERF替代梯度。对于NSNN模型，内部噪声为N(0, 0.2²)。

　　我们使用的CNN基线采用的架构是：32C25-BN-16C11-BN-FC49-BN-PSoftPlus，其中BN表示批归一化操作，PSoftPlus表示参数化SoftPlus激活。训练规范遵循先前工作⁶⁹中的实现。