Noisy Networks for Exploration
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Published as a conference paper at ICLR 2018
ABSTRACT
我们介绍了NoisyNet,一种在其权重中添加了参数噪声的深度强化学习智能体,并表明智能体策略的诱导随机性可以用来帮助有效的探索。噪声的参数与剩余的网络权重一起通过梯度下降来学习。NoisyNet实现起来很简单,并且几乎不增加计算开销。我们发现,用NoisyNet取代A3C、DQN和Dueling智能体的传统探索启发式(分别是熵奖励和ε-贪婪),在广泛的Atari游戏中产生了更高的分数,在某些情况下,将智能体从亚人类性能提升到超人类性能。
1 INTRODUCTION
尽管对强化学习(RL)中的有效探索方法进行了大量研究(Kearns & Singh, 2002; Jaksch et al., 2010),但大多数探索启发法都依赖于智能体策略的随机扰动,如ε-贪婪(Sutton & Barto, 1998)或熵正则化(Williams, 1992),以诱导新的行为。然而,这种局部“抖动”扰动不太可能导致在许多环境中进行有效探索所需的大规模行为模式(Osband et al., 2017)。
面对不确定性的乐观主义是强化学习中常见的探索启发式方法。这种启发式的各种形式通常伴随着对智能体性能的理论保证(Azar et al., 2017; Lattimore et al., 2013; Jaksch et al., 2010; Auer & Ortner, 2007; Kearns & Singh, 2002)。然而,这些方法通常局限于小状态-动作空间或线性函数近似,并且不容易应用于更复杂的函数近似器,如神经网络(除了(Geist & Pietquin, 2010a;b)的工作,但它没有收敛保证)。一种更结构化的探索方法是用一个额外的内在动机项来增强环境的奖励信号(Singh et al., 2004),该项明确奖励新发现。已经提出了许多这样的术语,包括学习进度(Oudeyer & Kaplan, 2007)、压缩进度(Schmidhuber, 2010)、变分信息最大化(Houthooft et al., 2016)和预测增益(Bellemare et al., 2016)。一个问题是,这些方法将泛化机制与探索机制分开;内在奖励的衡量标准,以及重要的是,它相对于环境奖励的权重,必须由实验者选择,而不是从与环境的互动中学习。如果没有适当的注意,最优策略可能会被改变,甚至完全被内在的奖励所掩盖;此外,通常需要抖动扰动以及内在奖励,以确保鲁棒的探索(Ostrovski et al., 2017)。例如,利用进化或黑盒算法对策略空间本身进行探索(Moriarty et al., 1999; Fix & Geist, 2012; Salimans et al., 2017),通常需要与环境进行许多长期的互动。尽管这些算法非常通用,可以应用于任何类型的参数策略(包括神经网络),但它们通常不是数据高效的,并且需要模拟器来进行许多策略评估。
我们提出了一种简单的替代方法,称为NoisyNet,其中使用网络权重的学习扰动来驱动探索。关键的见解是,权重向量的一次变化可以在多个时间步长上导致策略的一致且可能非常复杂的状态相关变化,这与抖动方法不同,抖动方法在每一步都会向策略中添加去相关(在ε-贪婪的情况下,与状态无关)的噪声。扰动是从噪声分布中采样的。扰动的方差是一个可以被认为是注入噪声的能量的参数。这些方差参数是使用来自强化学习损失函数的梯度以及智能体的其他参数来学习的。该方法不同于参数压缩方案,如变分推理(Hinton & Van Camp, 1993; Bishop, 1995; Graves, 2011; Blundell et al., 2015; Gal & Ghahramani, 2016)和平坦最小搜索(Hochreiter & Schmidhuber, 1997),因为我们在训练过程中不保持权重的显式分布,而是简单地在参数中注入噪声并自动调整其强度。因此,它也不同于Thompson采样(Thompson, 1933; Lipton et al., 2016),因为我们的智能体的参数分布不一定收敛于后验分布的近似值。
在高层,我们的算法是一个随机值函数,其中函数形式是一个神经网络。随机值函数提供了一种可证明有效的探索方法(Osband et al., 2014)。之前将这种方法扩展到深度神经网络的尝试需要网络部分的许多副本(Osband et al., 2016)。相比之下,在我们的NoisyNet方法中,当网络的线性层中的参数数量加倍时,由于权重是噪声的简单仿射变换,因此计算复杂性通常仍然由激活乘法的权重而不是生成权重的成本所支配。此外,它还适用于策略梯度方法,如A3C开箱即用(Mnih et al., 2016)。最近(独立于我们的工作),Plappert等人(2017)提出了一种类似的技术,其中将恒定高斯噪声添加到网络的参数中。因此,我们的方法的不同之处在于网络适应噪声随时间注入的能力,并且它不限于高斯噪声分布。我们需要强调的是,在不同名称的监督学习和优化文献中(例如,神经扩散过程(Mobahi, 2016)和分级优化(Hazan et al., 2016)),已经对注入噪声以改进优化过程的想法进行了深入研究。这些方法通常依赖于不可训练的消失大小的噪声,而不是通过梯度下降来调整噪声量的NoisyNet。
NoisyNet也可以适用于任何深度RL算法,我们通过提供DQN (Mnih et al., 2015)、Dueling (Wang et al., 2016)和A3C (Mnih et al., 2016)算法的NoisyNet版本来证明这种多功能性。在57个Atari游戏上的实验表明,与基线算法相比,NoisyNet-DQN和NoisyNet-Dueling在没有显著额外计算成本和需要调整的超参数较少的情况下实现了惊人的增益。此外,A3C的噪声版本提供了一些优于基线的改进。
2 BACKGROUND
本节提供了马尔可夫决策过程(MDP)和深度RL的数学背景,包括Q学习、对偶和actor-critic方法。
2.1 MARKOV DECISION PROCESSES AND REINFORCEMENT LEARNING


2.2 DEEP REINFORCEMENT LEARNING


3 NOISYNETS FOR REINFORCEMENT LEARNING
NoisyNet是一种神经网络,其权重和偏差受到噪声的参数函数的扰动。这些参数通过梯度下降进行调整。更准确地说,设y = fθ(x)是一个由噪声参数θ的向量参数化的神经网络,该向量取输入x和输出y。我们将噪声参数θ表示为![]() ,其中
,其中![]() 是一组可学习参数的向量,ε是一个具有固定统计的零均值噪声向量,
是一组可学习参数的向量,ε是一个具有固定统计的零均值噪声向量, 表示逐元素乘法。神经网络的常规损失由对噪声ε的期望包裹着:
表示逐元素乘法。神经网络的常规损失由对噪声ε的期望包裹着:![]() 。现在对参数集ζ进行优化。
。现在对参数集ζ进行优化。
考虑具有p个输入和q个输出的神经网络的线性层,由:

其中![]() 是层输入,
是层输入,![]() 是权重矩阵,
是权重矩阵,![]() 是偏差。相应的噪声线性层定义为:
是偏差。相应的噪声线性层定义为:
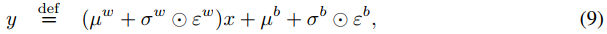
其中,![]() 和
和![]() 分别取代公式(8)中的w和b。参数
分别取代公式(8)中的w和b。参数![]() 、
、![]() 、
、![]() 和
和![]() 是可学习的,而
是可学习的,而![]() 和
和![]() 是噪声随机变量(该分布的具体选择如下所述)。我们在图4中提供了噪声线性层的图形表示(见附录B)。
是噪声随机变量(该分布的具体选择如下所述)。我们在图4中提供了噪声线性层的图形表示(见附录B)。
我们现在转向噪声网络中线性层的噪声分布的显式实例。我们探索了两种选择:独立高斯噪声,它使用每个权重的独立高斯噪声条目;因子化高斯噪声,其使用每个输出的独立噪声和每个输入的另一个独立噪声。在我们的算法中,使用因子化高斯噪声的主要原因是为了减少随机数生成的计算时间。在诸如DQN和Dueling之类的单线程智能体的情况下,这种计算开销尤其令人望而却步。因此,我们对DQN和Dueling使用因子化噪声,对分布式A3C使用独立噪声(其计算时间不是主要问题)。
(a)独立高斯噪声:应用于每个权重和偏差的噪声是独立的,其中随机矩阵εw(随机向量εb)的每个条目![]() (每个条目
(每个条目![]() )都是从单位高斯分布中提取的。这意味着,对于每个噪声线性层,存在pq+q个噪声变量(对于层的p个输入和q个输出)。
)都是从单位高斯分布中提取的。这意味着,对于每个噪声线性层,存在pq+q个噪声变量(对于层的p个输入和q个输出)。
(b)因子化高斯噪声:通过因子分解![]() ,我们可以使用p个单位高斯变量εi表示输入的噪声,使用q个单位高斯变量εj表示输出的噪声(因此总共p+q个单位高斯变数)。每个
,我们可以使用p个单位高斯变量εi表示输入的噪声,使用q个单位高斯变量εj表示输出的噪声(因此总共p+q个单位高斯变数)。每个![]() 和
和![]() 可以写成:
可以写成:

其中 f 是实值函数。在我们的实验中,我们使用了![]() 。注意,对于偏差公式(11),我们可以设置f(x)=x,但我们决定对于权重和偏差保持相同的输出噪声。
。注意,对于偏差公式(11),我们可以设置f(x)=x,但我们决定对于权重和偏差保持相同的输出噪声。
由于噪声网络的损失![]() 是对噪声的期望,因此可以直接获得梯度:
是对噪声的期望,因此可以直接获得梯度:
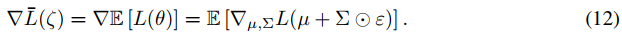
我们对上述梯度使用蒙特卡罗近似,在每个优化步骤取一个样本ξ:
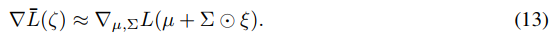
3.1 DEEP REINFORCEMENT LEARNING WITH NOISYNETS
我们现在转向我们对噪声网络的应用,以探索深度强化学习。噪声驱动了对许多强化学习方法的探索,为智能体和手头的RL任务提供了外部的随机性来源。这种噪声的规模要么在广泛的任务范围内手动调整(就像在诸如DQN或A3C的通用智能体中的实践一样),要么可以按任务手动调整。在这里,我们提出根据需要,使用噪声网络训练来降低(或提高)注入神经网络参数的噪声水平,从而自动调整添加到用于探索的智能体中的噪声水平。
噪声网络智能体在每个优化步骤之后对一组新的参数进行采样。在优化步骤之间,智能体根据一组固定的参数(权重和偏差)进行操作。这确保了智能体始终根据从当前噪声分布中提取的参数来进行操作。
Deep Q-Networks (DQN) and Dueling. 我们对DQN和Dueling都进行了以下修改:首先,不再使用ε-贪婪,而是贪婪地优化(随机)动作-价值函数。其次,将价值网络的全连接层参数化为噪声网络,其中参数取自每个重放步骤后的噪声网络参数分布。我们使用了因子化高斯噪声,如第3节(b)中所述。对于重放,当前噪声网络参数样本在整个batch中保持固定。由于DQN和Dueling对每个动作步骤进行一步优化,因此在每个动作之前对噪声网络参数进行重新采样。我们将DQN和Dueling的新改进分别称为NoisyNet-DQN和NoisyNet-Dueling。
我们现在提供了我们的DQN变体正在最小化的损失函数的细节。当用网络中的噪声层替换线性层时(也在目标网络中),参数化动作-价值函数Q(x, a, ε, ζ)(或Q(x, a, ε', ζ-))可以被视为随机变量,DQN损失变为NoisyNet-DQN损失:
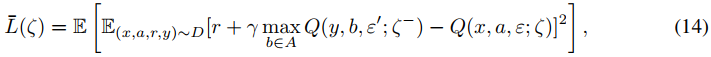
其中外部期望是关于噪声价值函数Q(x, a, ε, ζ)的噪声变量ε和噪声目标价值函数Q(x, a, ε', ζ-)的噪声变量ε'的分布。计算损失的无偏估计是简单的,因为我们只需要为重放缓存中的每个转换计算目标网络的一个实例和在线网络的一个实例。我们生成这些独立的噪声,以避免由于目标网络和在线网络中的噪声之间的相关性而产生的偏差。关于动作选择,我们为在线网络生成另一个独立样本ε'',并且我们相对于相应的输出动作-价值函数贪婪地行动。
类似地,NoisyNet-Dueling的损失函数定义为:
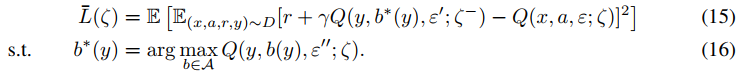
附录C.1中提供了这两种算法。
Asynchronous Advantage Actor Critic (A3C). A3C以类似于DQN的方式进行了修改:首先,去除了策略损失的熵加成。其次,策略网络的全连接层被参数化为噪声网络。我们使用独立高斯噪声,如第3节(a)所述。在A3C中,没有明确的探索性动作选择方案(例如ε-贪婪);并且所选择的动作总是来自当前策略。出于这个原因,经常添加策略损失的熵加成来阻止导致确定性策略的更新。然而,当向网络添加噪声权重时,对这些参数进行采样对应于选择不同的当前策略,这自然有利于探索。作为在策略空间中直接探索的结果,因此可以省略策略上的人工熵损失。在每个优化步骤之后对策略网络的新参数进行采样,并且由于A3C使用n个步骤回报,因此每n个步骤进行一次优化。我们把A3C的这种改型称为NoisyNet-A3C。
事实上,当用噪声线性层代替线性层时(现在注意到有噪声网络的参数ζ),我们通过大小为k的rollout获得以下回报估计:
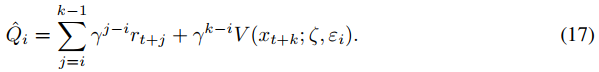
由于A3C是一种同策算法,当网络的噪声对于整个rollout是一致的时,梯度是无偏的。动作价值函数![]() 之间的一致性是通过让噪声在每个rollout中都相同来确保的,即
之间的一致性是通过让噪声在每个rollout中都相同来确保的,即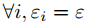 。附录A中提供了更多细节,附录C.2中给出了算法。
。附录A中提供了更多细节,附录C.2中给出了算法。
3.2 INITIALISATION OF NOISY NETWORK
在无因子化噪声网络的情况下,参数µ和σ初始化如下。每个元素µi,j是从独立的均匀分布![]() 中采样的,其中p是对应线性层的输入数量,对于所有参数,每个元素σi,j被简单地设置为0.017。之所以选择这种特定的初始化,是因为类似的值对于Fortunato等人(2017)中描述的监督学习任务效果良好,其中后验方差和先验方差的初始化是相关的。我们还没有对这个参数进行调整,但我们认为,在同一尺度上的不同值应该会提供类似的结果。
中采样的,其中p是对应线性层的输入数量,对于所有参数,每个元素σi,j被简单地设置为0.017。之所以选择这种特定的初始化,是因为类似的值对于Fortunato等人(2017)中描述的监督学习任务效果良好,其中后验方差和先验方差的初始化是相关的。我们还没有对这个参数进行调整,但我们认为,在同一尺度上的不同值应该会提供类似的结果。
对于因子化噪声网络,每个元素µi,j由来自独立均匀分布![]() 的样本初始化,每个元素σi,j初始化为常数
的样本初始化,每个元素σi,j初始化为常数![]() 。超参数σ0设置为0.5。
。超参数σ0设置为0.5。
4 RESULTS
我们在57个Atari游戏中评估了噪声网络智能体的性能(Bellemare et al., 2015),并与没有噪声网络的基线进行了比较,这些基线依赖于原始的探索方法(ε-贪婪和熵加成)。
4.1 TRAINING DETAILS AND PERFORMANCE
我们使用随机启动无操作方案进行训练和评估,如原始DQN论文所述(Mnih et al., 2015)。评估模式与Mnih et al. (2016)的评估模式相同。在训练结束后,随机重新开始比赛进行评估。在训练期间,通过暂停学习并评估500K帧的最新智能体,在环境中每1M帧评估智能体的原始平均分数。回合被截断为108K帧(或30分钟的模拟播放)(van Hasselt et al., 2016)。
我们考虑了三种基线智能体:DQN (Mnih et al., 2015)、Dueling算法的duel clip变体(Wang et al., 2016)和A3C (Mnih et al., 2016)。DQN和A3C智能体分别针对200M和320M帧进行训练。在每种情况下,我们都将相应原始论文中的神经网络架构用于基线和NoisyNet变体。对于NoisyNet变体,我们使用了与各自原始论文中相同的超参数作为基线。
我们使用人类归一化分数比较了智能体的绝对性能:
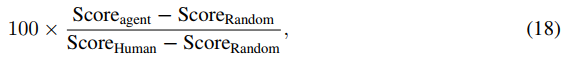
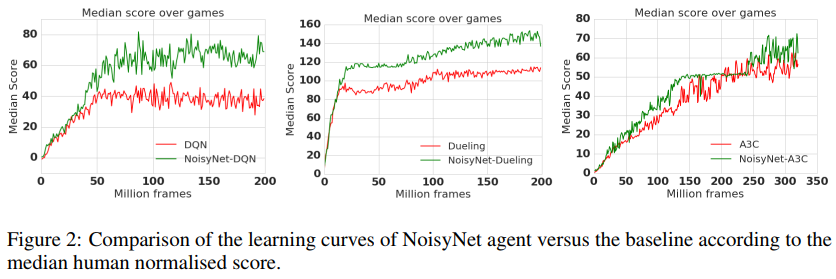
其中人类和随机分数与Wang等人(2016)的相同。请注意,对于随机智能体,人类归一化分数为零,而对于人类级别的性能,则为100。每次游戏的最大分数是通过获得智能体的最大原始分数,然后对三个种子进行平均来计算的。然而,为了计算图2中的人类归一化分数,每1M帧评估一次原始分数,并在三个种子上取均值。智能体的整体性能是通过Atari所有57个游戏中人类归一化分数的均值和中位数来衡量的。
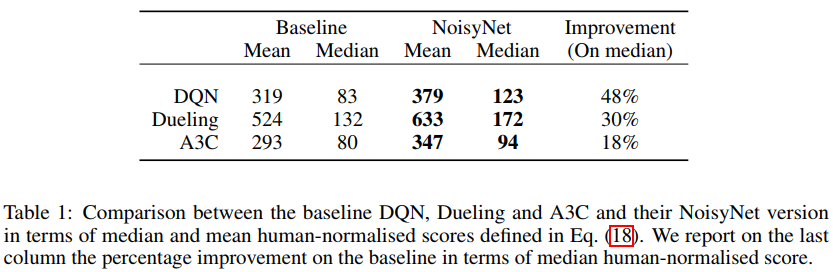
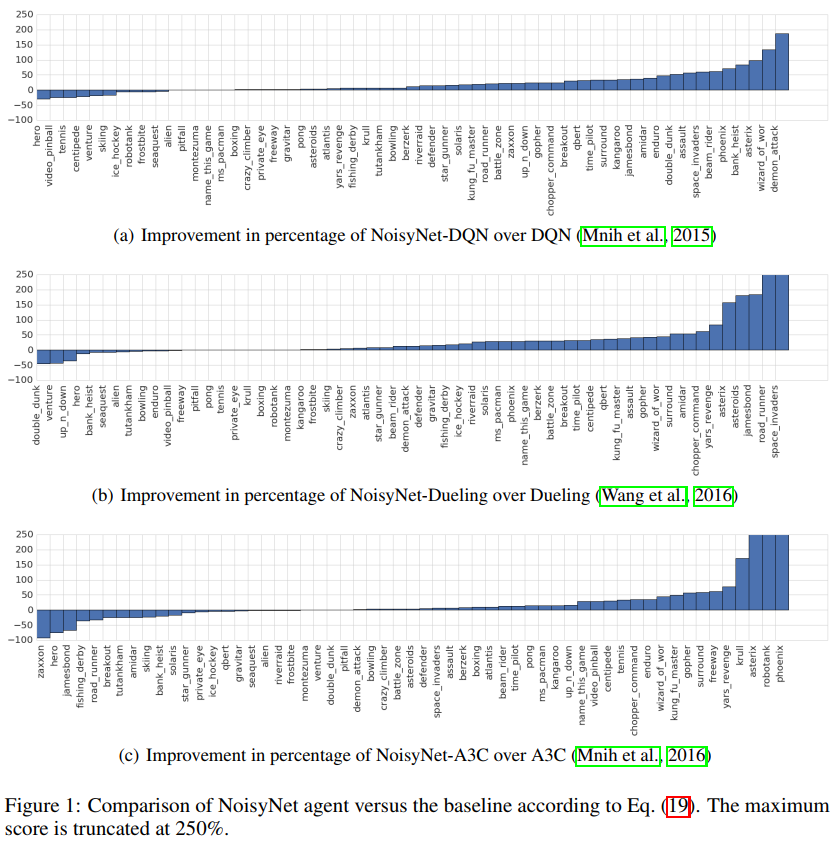
Atari所有57个游戏的汇总结果如表1所示,而每个游戏的个人分数如附录E中的表3所示。通过使用NoisyNet,所有智能体的人类归一化分数中值都得到了提高,在人类归一化分数中值的基础上增加了至少18个百分点(在A3C的情况下)和最多48个百分点(DQN)。所有智能体的平均人类归一化分数也显著提高。有趣的是,依赖于DQN的多次修改的Dueling案例表明,NoisyNet与DQN的其他几个改进是正交的。我们还将NoisyNet智能体的相对性能与没有噪声网络的相应基线智能体进行了比较:
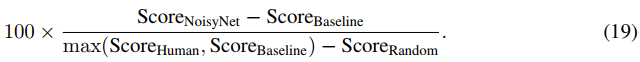
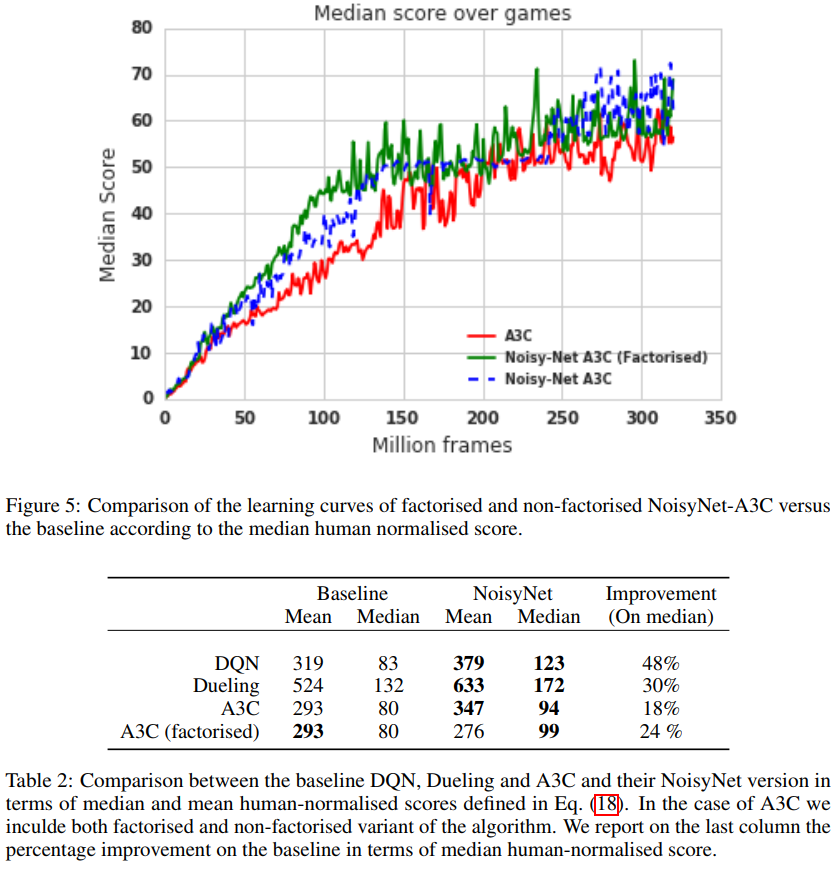
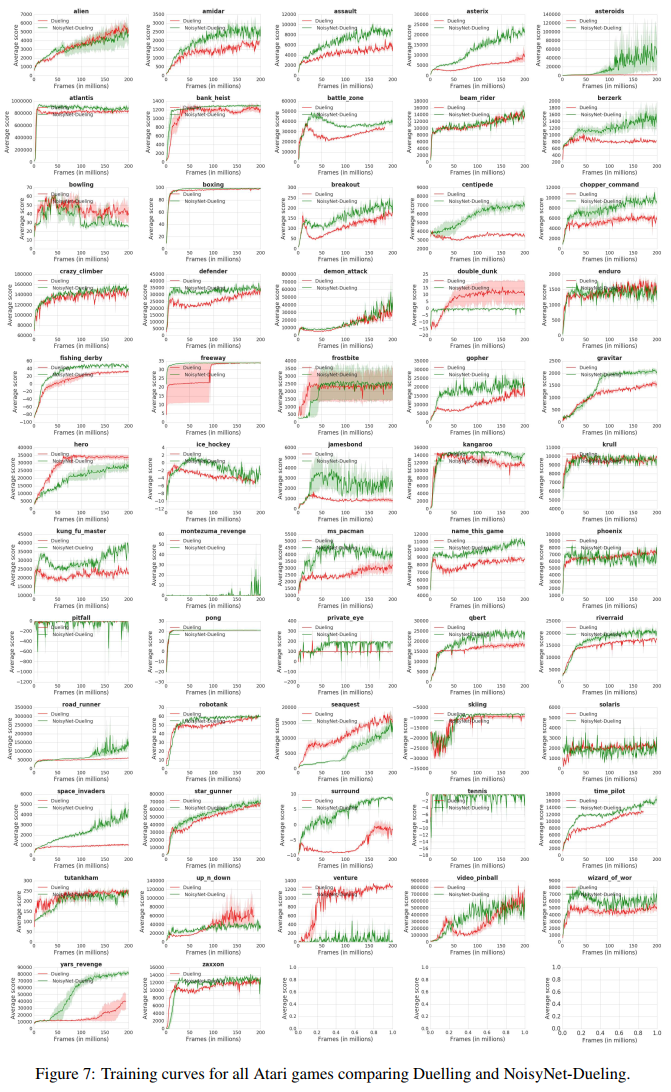
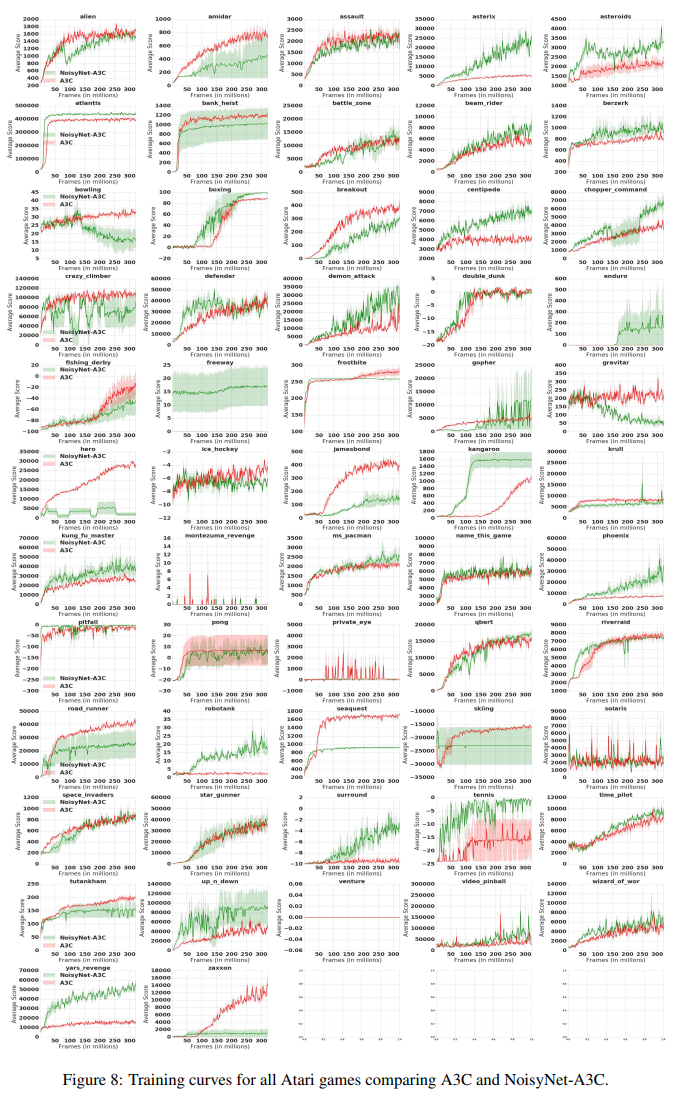
和以前一样,每个游戏的分数是通过取每次游戏的最大性能,然后对三个种子进行平均来计算的。相对人类归一化分数如图1所示。可以看出,相对于相应的基线,NoisyNet智能体(DQN、Dueling和A3C)在大多数游戏中的性能更好,在某些情况下甚至有相当大的优势。同样,从图2的学习曲线中可以明显看出,在整个学习过程中,与相应的基线相比,NoisyNet智能体产生了优越的性能。这种改进在NoisyNet-DQN和NoisyNet-Dueling的情况下尤其显著。同样在一些游戏中,NoisyNet智能体提供了朴素智能体性能的数量级改进;如附录E中的表3所示,分别为DQN、Dueling和A3C的个人游戏分数和图6、7和8中的学习曲线图。我们还进行了一些实验,评估了具有因子化噪声的NoisyNet-A3C的性能。我们在图5和表2中报告了相应的学习曲线和分数(见附录D)。这一结果表明,使用因子化噪声不会导致A3C性能的任何显著降低。相反,它似乎在提高中位分数和加快学习过程方面具有积极作用。
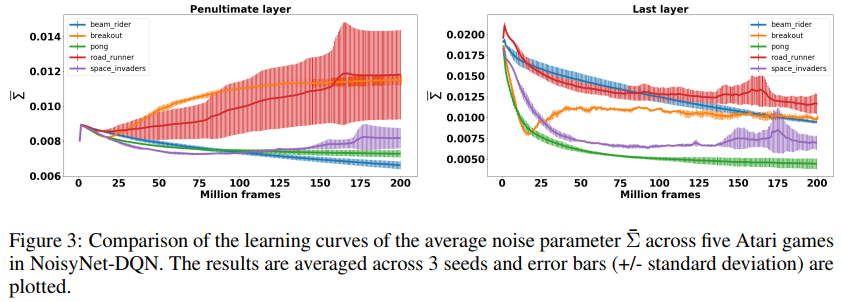
4.2 ANALYSIS OF LEARNING IN NOISY LAYERS
在本小节中,我们试图提供一些关于噪声网络如何影响智能体的学习过程和探索行为的见解。特别是,我们专注于分析噪声权重σw和σb在整个学习过程中的演变。我们首先注意到,由于L(ζ)是ζ的正连续函数,因此总是存在损失L(ξ)的确定性优化器(定义见公式(14))。因此,可以预期,为了获得确定性最优解,神经网络可以通过最终将σw和σb推向0来学习丢弃噪声条目。
为了验证这一假设,我们在整个学习过程中跟踪σw的变化。设![]() 表示噪声层的第 i 个权重。然后,我们定义
表示噪声层的第 i 个权重。然后,我们定义![]() ,噪声层的
,噪声层的![]() 的平均绝对值,如下:
的平均绝对值,如下:

直观地说,![]() 提供了噪声层的随机性的一些度量。我们在图3中报告了3个种子的
提供了噪声层的随机性的一些度量。我们在图3中报告了3个种子的![]() 平均值的学习曲线,用于NoisyNet-DQN智能体中的Atari游戏的选择。我们观察到,在所有情况下,网络最后一层的
平均值的学习曲线,用于NoisyNet-DQN智能体中的Atari游戏的选择。我们观察到,在所有情况下,网络最后一层的![]() 随着学习的进行而减少,而在倒数第二层的情况下,这种情况只发生在5个游戏中的2个(Pong和BeamRider),而在剩下的3个游戏中,
随着学习的进行而减少,而在倒数第二层的情况下,这种情况只发生在5个游戏中的2个(Pong和BeamRider),而在剩下的3个游戏中,![]() 实际上增加了。这表明,在NoisyNet-DQN的情况下,智能体不一定像人们预期的那样朝着确定性解决方案发展。另一个有趣的观察结果是,
实际上增加了。这表明,在NoisyNet-DQN的情况下,智能体不一定像人们预期的那样朝着确定性解决方案发展。另一个有趣的观察结果是,![]() 的演变方式因游戏而异,在某些情况下,从一个种子到另一个种子,这从误差条中可以明显看出。这表明NoisyNet产生了一种特定于问题的探索策略,而不是标准DQN中使用的固定探索策略。
的演变方式因游戏而异,在某些情况下,从一个种子到另一个种子,这从误差条中可以明显看出。这表明NoisyNet产生了一种特定于问题的探索策略,而不是标准DQN中使用的固定探索策略。
5 CONCLUSION
我们提出了一种探索深度强化学习的通用方法,该方法在三种不同的智能体架构中的许多Atari游戏中显示出显著的性能改进。特别是,我们观察到,在BeamRider、Asteroids和Freeway等标准DQN、Dueling和A3C与人类玩家相比表现不佳的游戏中,NoisyNet-DQN、NoisyNet-Dueling和NoisyNet-A3C分别实现了超人类性能。尽管由于修改了成本函数,性能的提高也可能来自优化方面,但NoisyNet引入的网络参数的不确定性是该方法的唯一探索机制。具有更大不确定性的权重会给策略做出的决策带来更多的可变性,这有可能采取探索性动作,但需要进行进一步的分析,以理清探索和优化效果。
NoisyNet的另一个优点是通过RL算法自动调整网络中注入的噪声量。这减轻了对任何超参数调整的需要(标准熵加成和贪婪类型的探索需要)。这也与许多其他方法形成了鲜明对比,这些方法添加了可能破坏学习稳定或改变最优策略的内在动机信号。NoisyNet方法的另一个有趣的特征是,探索的程度是有上下文的,并且根据每权重方差随状态而变化。虽然需要更多的梯度,但均值和方差参数上的梯度通过计算高效的仿射函数彼此相关,因此计算开销是边际的。自动微分使我们的方法的实现直接适应了许多现有方法。类似的随机化技术也可以应用于LSTM单元(Fortunato et al., 2017),并很容易扩展到强化学习,我们将其作为未来的工作。
值得注意的是NoisyNet探索策略不限于本文中考虑的基线。事实上,这一想法可以应用于任何可以用梯度下降训练的深度RL算法,包括DDPG (Lillicrap et al., 2015)、TRPO (Schulman et al., 2015)或分布式RL (C51)(Bellemare et al., 2017)。因此,我们认为这项工作是朝着制定普遍探索战略的目标迈出的一步。
A NOISYNET-A3C IMPLEMENTATION DETAILS


B NOISY LINEAR LAYER
在本附录中,我们提供了噪声层的图形表示。

C ALGORITHMS
C.1 NOISYNET-DQN AND NOISYNET-DUELING

C.2 NOISYNET-A3C

D COMPARISON BETWEEN NOISYNET-A3C (FACTORISED AND NON-FACTORISED NOISE) AND A3C
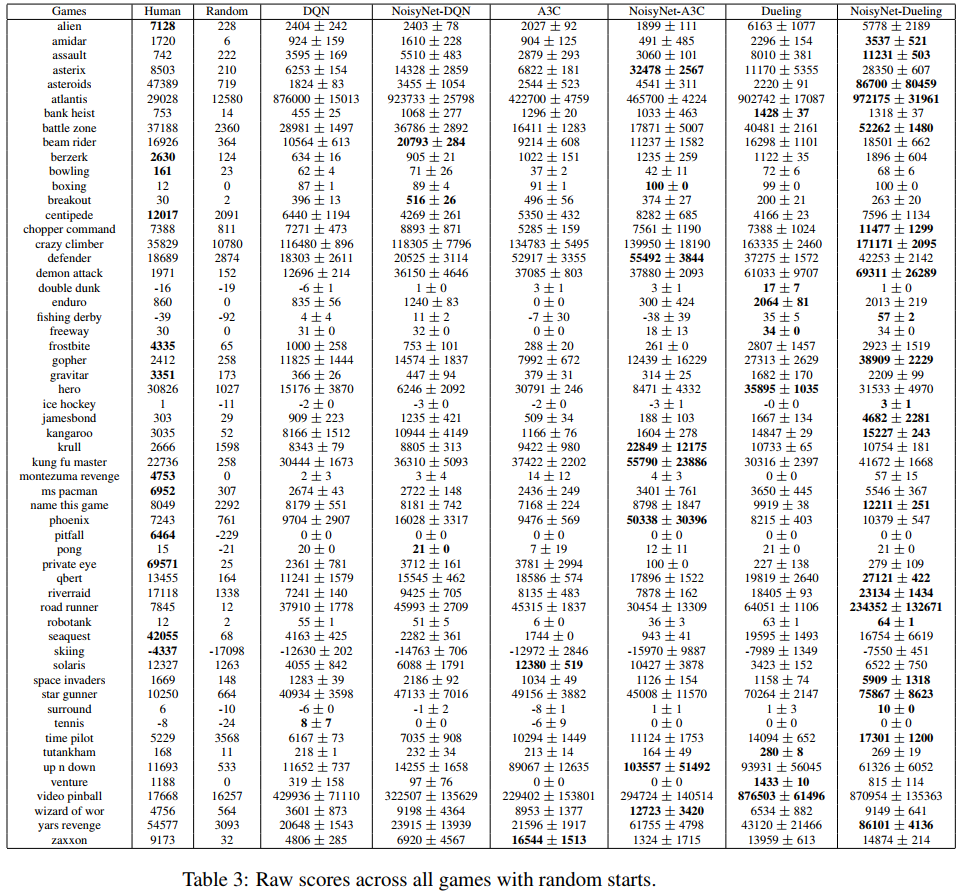
E LEARNING CURVES AND RAW SCORES
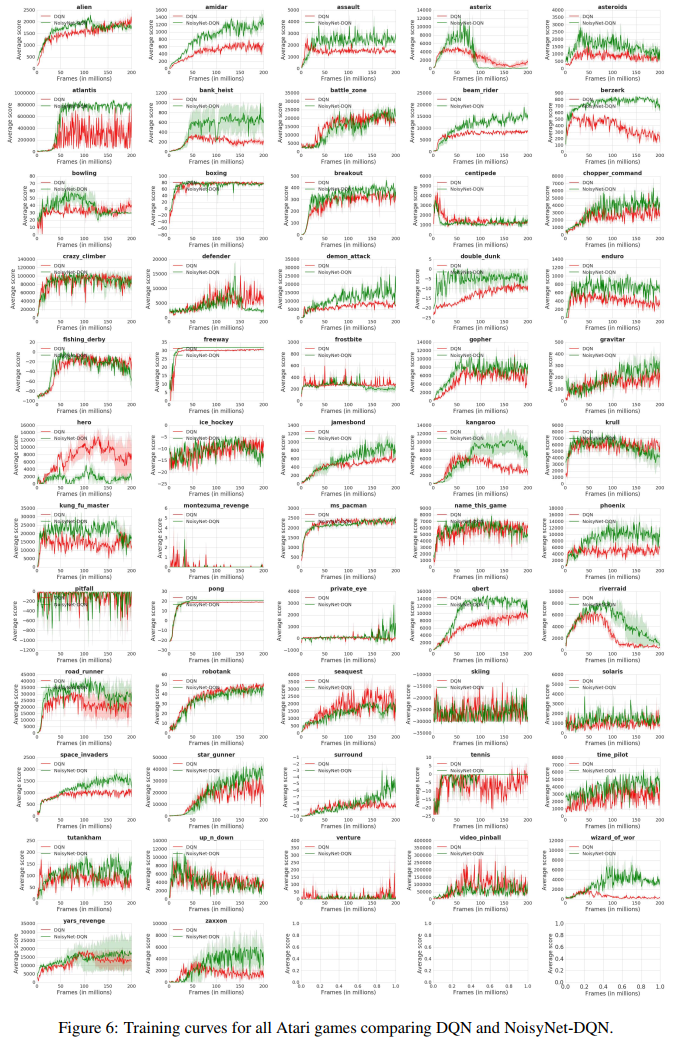
在这里,我们直接比较了DQN、Dueling DQN和A3C及其NoisyNet对应的表现,方法是显示57个Atari游戏中的每一个游戏的最大得分(表3),这是三个种子的平均值。在图6-8中,我们展示了各自的学习曲线。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号