Spike timing reshapes robustness against attacks in spiking neural networks
郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
同大组工作
Abstract
过去十年中，深度学习的成功部分笼罩在对抗攻击的阴影之下。相比之下，大脑在复杂的认知任务上要强大得多。利用大脑中神经元通过脉冲进行通信的优势，脉冲神经网络(SNN)正作为一种新型的神经网络模型出现，推动了人工神经网络和深度学习的理论研究和实证应用的前沿。神经科学研究表明，神经脉冲的精确时间在生物大脑的信息编码和感觉处理中起着重要作用。然而，脉冲时间在SNN中的作用很少被考虑，也远未被理解。在这里，我们系统地探讨了SNN中脉冲编码的时序机制，重点研究了系统对各种类型攻击的鲁棒性。我们发现，在不同的学习规则的帮助下，利用神经编码和解码中精确脉冲时间的编码原理，SNN可以实现更高的鲁棒性改进。我们的研究结果表明，脉冲时序编码在SNN中的实用性可以提高对攻击的鲁棒性，为开发下一代大脑启发的深度学习提供了一种可靠的编码原理的新方法。
Keywords: Spiking neural networks, adversarial robustness, spike timing, neural coding, neural decoding
1 Introduction
大脑如何处理信息的问题仍然是神经科学和人工智能领域中一个有趣的研究主题(Borst and Theunissen, 1999; Quiroga and Panzeri, 2009; Yamins and DiCarlo, 2016; Zador et al., 2023)。传统上，人们认为神经元通过脉冲的数量来编码感觉刺激，称为发放率编码，这一概念得到了20世纪初研究的支持(Adrian and Zotterman, 1926)。它已在多种感觉系统中被识别，如运动(Srivastava et al., 2017)和视觉皮层(Berry et al., 1997; Walker et al., 2020)，并被用于解释大脑中缓慢的感觉反应(Lu et al., 2001; Prescott and Sejnowski, 2008)。发放率编码一词具有丰富的含义，涵盖了群体编码(Auge et al., 2021)。然而，最近在过去十年中进行的研究表明，脉冲时间不仅在感觉刺激的编码中，而且在决策变量的编码中也起着关键作用(Stein et al., 2005; Gollisch and Meister, 2008; Quiroga and Panzeri, 2009)。因此，出现了一种用于感知和决策的神经元编码组合的概念，该组合以连贯的方式结合了发放率和时序编码(Mehta et al., 2002; Hong et al., 2016; Lankarany et al., 2019)。
在神经网络模型领域，人工神经网络(ANN)可以被视为一种发放率编码形式，因为它们模拟了神经元系统(Fukushima, 1975)。另一方面，脉冲神经网络(SNN)已成为受大脑启发的神经网络模型，利用脉冲神经单元来取代ANN中的神经模型(Maass, 1997; Bertens and Lee, 2020; Wozniak et al., 2020)。尽管如此，大多数SNN仍然在指定的时间范围内利用发放率，允许在计算中利用已建立的ANN (Sengupta et al., 2019; Rueckauer et al., 2017)。虽然某些SNN研究试图使用时间脉冲编码，但它们仅限于考虑几个脉冲(Park et al., 2020; Zhou et al, 2021; Stöckl and Maass, 2021; Göltz et al., 2021)，而没有计算发放率。因此，如何在SNN中实现同时结合发放率和脉冲时序的混合神经编码方案的问题仍然不清楚，脉冲时序在SNN的作用在很大程度上仍未被探索。在这项研究中，我们提出了一种新的神经编码方法，将脉冲时间序列嵌入到发放率SNN模型中。这种方法建立在SNN模型的发放率编码的当前进展的基础上，同时为单个脉冲之外的脉冲时序的作用提供了新的视角。
我们在一系列旨在增强抵御攻击的鲁棒性的任务中展示了我们提出的方法的有效性。即使面对不断变化的环境，我们的大脑也具有强大地执行各种功能的非凡能力(Denève et al., 2017)。相比之下，当前的ANN深度学习模型在面对对抗攻击时缺乏鲁棒性。即使对人眼容易看到的输入图像进行微小修改，也会导致ANN产生不准确的预测(Goodfellow et al., 2015)。尽管最近的进展允许高精度地训练生物可解释的SNN (Wu et al., 2019; Yin et al., 2021; Fang et al., 2021a)，但SNN对于对抗攻击的易感性仍然知之甚少(Ding et al., 2022)。在这项研究中，我们通过使用各种类型的学习规则，研究了脉冲时序机制与ANN相比在神经编码和解码方面的潜在好处。我们从这些多个角度的研究结果表明，脉冲时序机制的结合可以显著增强SNN的鲁棒性，特别是在对SNN学习进行对抗攻击的情况下。
2 Results
2.1 Rate-based SNNs gain robustness through synchronization schemes.
发放率编码主要使用脉冲频率对信息进行编码(Adrian and Zotterman, 1926)。这里，“发放率”术语的含义仅限于一个时间窗口内的平均发放率。SNN的最新进展表明，可以通过权重重新缩放将ANN转换为基于发放率的SNN (Cao et al., 2015; Diehl et al., 2015)。基于转换理论，SNN主要以发放率对信息进行编码，这近似于在有限的离散时间步长内模拟ANN的激活。为了验证脉冲时序离散化带来的对抗扰动(或攻击)的优势，我们训练了两个具有100个隐藏神经元的三层神经网络，在MNIST和Fashion MNIST (FMNIST)数据集上执行分类任务，并将其转换为具有积分和激发(IF)神经元的SNN。这使得比较采用扩展时间维度的可变发放率编码方案的SNN(图1(B))与基于ReLU的ANN之间的差异是公平的。此外，转换使我们能够从具有可微分激活的朴素ANN进行白盒攻击。
我们首先考虑Poisson编码，其中转换后的SNN接收与像素强度成比例的固定频率的伯努利采样脉冲。先前的研究已经证明，转换后的SNN的性能随着模拟时间的增加而增加(Rueckauer et al., 2017)。在这里，我们测试了使用泊松编码转换的SNN的鲁棒性是否与模拟时间有关。根据时变转换损失(ANN精度减去SNN精度)，我们手动选择了三个模拟时间值来测试SNN的鲁棒性，即“高精度损失”(高)、“低精度损失”(中)和“高精度”(低)。对于Fashion MNIST数据集，这三个值分别为6 ms、12 ms和24 ms (图1(C))。然后，我们对这些SNN进行了白盒迭代梯度对抗攻击。我们观察到，当攻击强度ε较大(=0.5)时，SNN的鲁棒性略有提高，“精度损失高”。然而，Poisson编码的整体鲁棒性可以忽略不计。
除了Poisson编码，转换后的SNN还允许直接输入恒定的“电流”，表示为“Current编码”。这种编码策略可以为转换后的SNN带来更好的准确性(Sharmin et al., 2020; Ding et al., 2021)，因此成为最流行的发放率编码方案之一。为了比较Poisson编码和Current编码，我们在白盒PGD-l2 (ε=0.5)和FGSM (ε=0.1)攻击下绘制了MNIST数据集上的时变分类精度(图1(D))。Poisson编码和Current编码的SNN曲线的趋势几乎相同。精度图首先随着清洁精度的增加而增加。然而，延长的模拟时间提高了浮点ANN激活的近似性，并阻碍了脉冲时序离散化引起的鲁棒特性。简而言之，模拟时间的选择对于基于发放率的转换SNN的鲁棒性至关重要。例如，对于MNIST数据集，当用强度为0.5的PGD-l2攻击时，运行9 ms的转换SNN比ANN的鲁棒性高6.8%。为了进一步分析鲁棒性背后的根本原因，我们计算了被攻击的SNN的发放率和隐藏神经元的被攻击的ANN激活之间的距离(l2和l∞)，以及被攻击的SNN的发放率与隐藏神经元的干净SNN之间的距离(图1(E))。我们发现，在SNN变得更加鲁棒的过程中，SNN的发放率接近ANN激活这一事实并不受影响。主要区别在于干净的SNN和被攻击的SNN之间的关系。发放率之间的距离首先通过注入噪声的低分辨率量化而增加。这种增加的趋势可以帮助解释为什么转换后的模型在较低的模拟时间下更鲁棒。
Poisson编码和Current编码在时间窗口中对信息进行统一编码，使SNN和ANN的输出在长时间模拟后更加接近。因此，SNN将很难表现出区别。在这里，我们设计了一种特殊的具有同步的确定性发放率编码(缩写为Rate-Syn)：平均发放率对应于0-1浮点输入像素强度，所有脉冲将在一个时间窗口内紧密排列，并且这些窗口将同步结束(参见图1(B))。关于三种编码方案的可视化，我们参考补充图S1。图1(D)表明，关于模拟时间的攻击精度显著高于Poisson编码和Current编码。在PGD-l2 (ε=0.5)攻击下，Rate-Syn编码的精度达到96.41%。请注意，在最后几个时间步骤中，精度略有下降。图1(E)中的距离可以帮助解释正在发生的事情。研究表明，使用Rate-Syn编码显著降低了干净发放率和攻击发放率之间的l2和l∞距离，这是先前认为的基于发放率的SNN的鲁棒性的原因。直观地说，与Poisson编码相比，Rate-Syn编码将推迟脉冲时间。因此，我们收集并计算了隐藏神经元群体在攻击和不攻击下的瞬时发放率(图1(F))，并发现Rate-Syn编码最初的整体发放率较低，实际上需要更多的时间来弥补整体发放率，并且Rate-Syn编码的发放率不断增加。当编码时间结束时，Rate-Syn在攻击下的鲁棒性会降低。
2.2 Dedicated training algorithms help spiking neural networks to further improve robustness.
从上面的分析来看，ANN可以通过转换为SNN来提高鲁棒性。基于转换的方法通常依赖于无泄漏的IF神经元。这并不是SNN为鲁棒性带来的全部：由于泄漏效应，具有泄漏因子的神经元模型已被证明拥有更大的鲁棒性(Sharmin et al., 2019)。如何训练这些SNN现在已经成为一个热门的研究课题(Neftci et al., 2019; Fang et al., 2021b; Yin et al., 2023)。训练方法准确地操纵了脉冲序列，这在很大程度上可以分为两类：基于激活的反向传播(Act-BP)(Wu et al., 2018)和基于时序的反向传播)(Temp-BP)(Zhang and Li, 2020; Kheradpisheh and Masquelier, 2020)。这两类的主要差异在于梯度传播的过程(见图2(A))。Act-BP训练使不可微分的脉冲平滑并使梯度通过膜电位V，而Temp-BP训练将梯度传播到脉冲时间 t。我们跟随(Wu et al., 2018)和(Zhang and Li, 2020)分别实现了Act-BP和Temp-BP。两种训练算法带来的权重分布确实不同(图2(B))。我们在Fashion MNIST数据集上用Act-BP和Temp-BP训练了具有Current、Poisson和Rate-Syn编码的SNN，并将其鲁棒性与转换(CVT) SNN和ANN的鲁棒性进行了比较。我们首先测试了黑盒FGSM攻击的效果。使用三种输入编码方法的性能可以从图2(C)(D)(E)中看出。在这三个实验中，我们大致观察到的鲁棒性从高到低的顺序是：Temp-BP SNN、Act-BP SNN、CVT SNN和ANN。结果表明，尽管改变了训练方法，输入编码也会影响鲁棒性。为了进一步了解输入编码的影响，我们在图2(I)中绘制了FGSM攻击下10 ms内精度的变化。注意，Rate-Syn编码的同步时间也是10ms。我们发现，对于Poisson编码，较短时间的鲁棒性几乎不受影响。对于Rate-Syn，随着编码的发展，其性能不断提高，最终超过了Poisson编码的性能。
训练中对脉冲序列的感知提高了扰动后的稳定性。令人惊讶的是，我们发现，与CVT SNN相比，由Act-BP和Temp-BP训练的SNN的鲁棒性不太容易受到脉冲时序变化的影响。我们以一定的频率随机丢弃泊松模式中的脉冲(图2(F))。Temp-BP SNN和Act-BP SNN也优于CVT SNN。
为了理解训练方法对特定攻击方法之外的影响，我们深入研究了梯度的特征。我们检验了梯度
乘以
的范数，其中
是被攻击序列，y是目标。
包含一阶泰勒多项式的信息，尽管SNN的梯度是不准确的。值越小表示鲁棒性越好。我们从图2(G)(H)中观察到，CVT SNN和ANN的范数大于Temp-BP SNN和Act-BP SNN，这可能有助于部分解释鲁棒性。
研究人员提出，使用替代梯度时也可以进行SNN攻击(Kundu et al., 2021)。我们使用了两组具有Current编码的模型作为防御和攻击模型，并进行了PGD-l∞ (ε=0.1)和BIM-l2 (ε=0.5)攻击。攻击下的模型精度和攻击成功率如图2(J)所示。
对于白盒攻击，我们发现自然可微ANN的白盒攻击比Act-BP和Temp-BP的生成攻击更强大。同时，我们发现Act-BP和Temp-BP的黑盒攻击能力也较弱。将ANN模型转换为SNN模型后，其攻击能力变化不大。最重要的是，我们发现Temp-BP和Act-BP SNN对ANN的黑盒攻击比ANN对Temp-BP或Act-BP的黑盒攻击弱。SNN独特的梯度近似方法使其具有更强的抗攻击能力和较弱的攻击能力。
2.3 Diverse combinations of neural encoding and decoding criteria enhance the robustness of SNNs.
我们已经知道，通过将特定于SNN的近似梯度结合到训练中，可以提高SNN的鲁棒性。此外，还可以通过调整解码策略来改变梯度。目前，最常用的解码策略是通过发放率，即根据输出神经元发放率的大小来确定模型预测(Lee et al., 2020; Sengupta et al., 2019)。此外，通过时序编码传递的精确脉冲时间包含丰富的信息，并且还被用于提供用于解码的误差信号(Kim et al., 2020)。为了测试时序编码对SNN的影响，TTFS是一种典型的时序编码策略，用于SNN中的编码和解码。如图3(C)所示，通过TTFS进行解码意味着预测和误差信号集中在初次脉冲的延迟上(简写为TTFS解码)，而不是发放率(简写为Rate解码)。我们使用Current编码、Rate-Syn编码和TTFS编码作为输入编码，使用Rate解码和TTFS解码作为解码方法。编码和解码方法的结合结合了Act-BP来在MNIST数据集上训练SNN：Current+Rate、Rate-Syn+Rate、TTFS+Rate、Current+TTFS、Rate-Syn+TTFS和TTFS+TTFS。
我们发现，在我们的实验中，组合的鲁棒性各不相同。我们将六个训练有素的SNN和ANN置于黑盒FGSM的攻击下(图3(D))。对于Current和Rate-Syn编码，TTFS解码有助于提高鲁棒性。同时，无论使用哪种解码方法，使用TTFS编码的模型的鲁棒性都很高。简而言之，与ANN相比，时序编码和解码的加入使该模型更能抵抗黑盒FGSM攻击。这些方法在PGD攻击下的性能相似，如补充图S3所示。
我们试图从两个角度解释鲁棒性的原因。首先，随着攻击强度的增加，我们记录了隐藏层中接收干净和攻击输入的神经元产生的脉冲序列，并计算了它们的Victor-Purpura距离(图3(E))。我们发现，具有较高扰动抗扰度的模型通常具有较小的脉冲距离。此外，我们随机选择了两个相互正交的FGSM扰动方向
并得到了一阶泰勒多项式
，其中ε1和ε2是[0, 1]中的标量。我们在图3(F)中的热图中给出了这些结果。研究发现，对于鲁棒性较差的组合Current+Rate，其一阶泰勒多项式的值总是较大，这意味着当施加扰动时，该组合很容易受到影响。相比之下，其他组合在热图中有更大的“谷”。这意味着有相当多的扰动不会给一阶泰勒多项式带来大的变化。对于在我们的实验中具有较强鲁棒性的TTFS+Rate和TTFS+TTFS这两种组合，热图几乎被“波谷”覆盖。我们还绘制了Temp-BP训练的SNN的结果，并得到了类似的诱导。
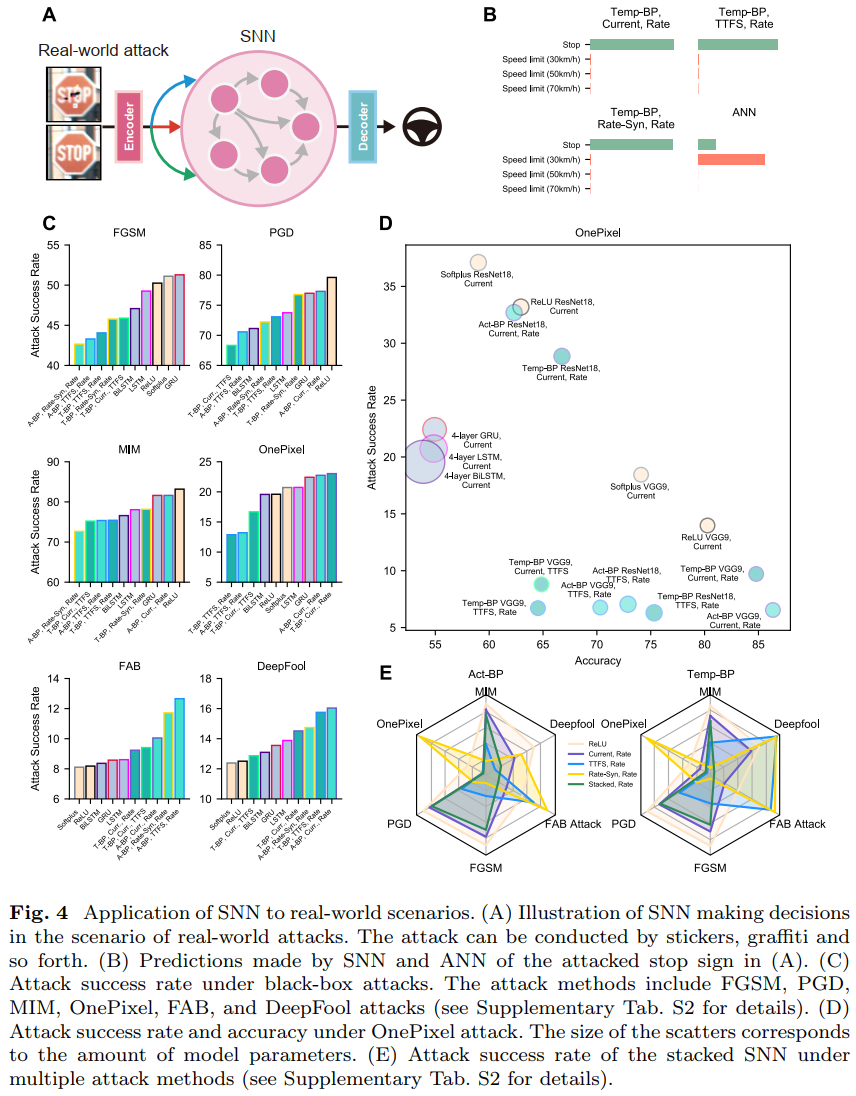
2.4 Application to real-world scenarios.
我们之前讨论了SNN的输入编码、输出解码和训练方法对鲁棒性的影响。即使对于黑盒攻击，在现实世界场景中也很难实现像素级的扰动。更可能的方法是应用真实世界的攻击，例如手动设计的贴纸、涂鸦(Eykholt et al., 2018)、激光(Duan et al., 2021)、反射(Liu et al., 2020)和其他手段。我们想知道SNN是否能够抵抗更多的攻击方法，并在日常场景中表现鲁棒。因此，我们在德国交通标志识别基准(GTSRB)数据集上进行了实验。GTSRB数据集包含日常生活中常见的43种交通标志的图像。
我们对SNN进行了分类任务训练，以模拟车辆上的安全关键应用。我们首先遵循Eykholt等人(2018)提出的方法，对测试数据集中的停止标志进行黑盒攻击。攻击的结果是，这些样本上出现了图案贴纸。这些对抗样本通过编码器输入SNN，输出序列的解码结果影响系统的决策(图4(A))。
我们比较了在相同网络规模下具有各种设置组合的ANN和SNN。实验表明，与ReLU激活的ANN获得的27.8%的精度相比，在Current+Rate设置下的Temp-BP SNN准确识别了55.6%的受攻击样本。对于图4(A)中的对抗样本，当ANN识别停车标志时，它将该标志识别为“限速(30km/h)”，并且该样本在某些设置下不会混淆SNN(图4(B))。
同时，我们还测试了这些SNN在更多扰动方法上的鲁棒性。我们训练了一个ReLU激活的ResNet18，并使用该模型构建黑盒攻击样本。攻击方法包括FGSM (Goodfellow et al., 2015)、PGD (Madry et al., 2018)、MIM (Dong et al., 2018.)、OnePixel (Su et al., 2019)、FAB (Croce and Hein, 2020)和DeepFool (Moosavi-Dezbulli et al., 2016)。我们还训练了Softplus激活的ANN以及具有门控递归单元(GRU)和长短期记忆(LSTM)的循环神经网络(RNN)进行比较。这些模型也有相同的神经元规模。我们比较了这些攻击的成功率。对于防御模型来说，较低的攻击成功率意味着更好的鲁棒性。我们对攻击成功率最低的前十个模型的结果进行了排序，并将其显示在图4(C)中。
对于OnePixel攻击，我们测试了更深SNN的性能，并绘制了散点图(图4(D))。请注意，散点的大小表示模型参数的数量。具体来说，我们对VGG9和ResNet18网络架构进行了实验。模型深度的增加并不能提高攻击成功率。对于一些由Temp-BP和Act-BP训练的SNN，由于更深层次架构带来的泛化能力的提高，对抗样本的准确性也得到了提高，攻击成功率大大降低，例如由Act-BP训练出的VGG9 SNN。
我们认为，对于不同的编码和解码组合，SNN的鲁棒性并不完全相同，并且大脑不使用单一的编码进行信号传输。因此，我们使用堆叠技术来集成使用Rate解码的VGG9 SNN (Wolpert, 1992)。堆叠技术从不同编码的三个模型中获得特征，并将这些特征连接起来。新特征用于重新训练线性SNN层并给出Rate解码预测。我们分别对Act-BP和Temp-BP SNN进行了集成，并测试了堆叠模型的性能。我们在雷达图中显示了这些模型相对于六种对抗方法的攻击成功率(图4(E))。与ReLU激活的ANN相比，任何单个编码方案都只能提供更好的抵抗某些攻击的能力。然而，堆叠模型对任何类型的攻击方法都提供了更好的鲁棒性，这表明在SNN中使用融合编码策略的好处。
3 Discussion
我们在本文中系统地证明了精确的脉冲时间有助于提高神经网络的鲁棒性，为理解大脑的鲁棒性提供了机会。我们从计算的角度给出了一条可行的人工智能安全路径，即利用SNN并充分采用精确的时序编码和解码来实现大脑启发的深度学习。特别是，我们发现，只需调整神经编码的同步性就可以提高鲁棒性，当使用特定于SNN的训练方法时，这一优势是显而易见的。此外，结合各种解码方案，我们可以实现具有损失景观感知的鲁棒训练。此外，当这些方案形成混合系统时，我们证明了混合模型对各种攻击方法的鲁棒性。
SNN是ANN的进化版本(Maass, 1997)，它自然地将时序能力扩展到神经网络(Rao et al., 2022)。然而，到目前为止，这种时序能力还没有得到很好的利用。神经网络的鲁棒性是一个很好的展示，说明了时序能力的重要性。特别是，我们设计了一种简洁的时序编码方法，仅通过调节输入神经元的开始和结束发放时间，就可以提高从神经网络转换而来的SNN模型的鲁棒性。先前的工作还发现，编码对SNN的鲁棒性很重要(Kundu et al., 2021; Kim et al., 2022)，但仍停留在对脉冲计数发放率编码的讨论中。事实上，如当前研究所示，脉冲计数发放率编码通过离散时间量化所能带来的鲁棒性增益非常有限。因此，我们设计了精确的输入编码策略来实现类似神经元同步的功能。该方案在使用ANN转换的权值时有效。这启发我们重新理解ANN：ANN并不缺乏防御能力，而是采用了无效的输入方案。鉴于神经元同步具有广泛的生物学基础(Womelsdorf et al., 2007)，并且神经编码的时间复用对于信息表征是有效的(Panzeri et al., 2010)，我们希望我们的模型能够帮助解释更复杂的生物功能。
由于我们采用了更复杂的SNN编码方案，因此需要考虑SNN的特定训练方案来帮助提高性能。训练方法的改变使SNN能够更好地利用时序的优势。SNN最近的一个重点是如何为SNN设计更好的训练算法。本文中提到的Act-BP和Temp-BP就是这些算法中的一种。Act-BP和Temp-BP代表两种类型的算法。Act-BP的反向传播过程对脉冲产生的完整动态过程进行了建模(Lee et al., 2020; Wu et al., 2018)，而Temp-BP更关注如何在训练过程中利用脉冲时序的稀疏性(Zhang and Li, 2020; Zhu et al., 2022)。在实验中，我们发现这两种训练方法都提高了SNN的鲁棒性。这表明，准确的脉冲时序编码需要SNN训练方法的帮助，而如何训练SNN对于利用时序信息至关重要。当然，SNN的训练方法也推动了SNN特定对抗方法的研究(Liang et al., 2023)。在我们的工作中，我们考虑了通过这些不同方法训练的网络执行攻击的能力。具有更强鲁棒性的模型无法提供更好的攻击能力。我们的研究结果可以启发一系列关于SNN攻击和防御的研究，以克服ANN目前面临的挑战(Davies, 2019)。
在采用特定于SNN的学习方法后，SNN可以利用不同的神经编码和解码方法。神经解码涉及神经元反应如何转化为有意义的标签(Nakai and Nishimoto, 2022; Suárez et al., 2021)。图像识别中最常见的解码方案是使用随时间变化的平均发放率作为模型预测的向量(Cao et al., 2015)。与编码类似，这实际上忽略了脉冲时序的积极影响。为此，我们集成了时序敏感的TTFS解码方案。伴随解码方案调整的是损失函数的变化，这改变了SNN对损失景观的感知。比较发放率解码和TTFS解码，我们发现它们对应于输入附近的一阶泰勒多项式景观中的差异。这可能是由于基于TTFS解码构建的损失函数更稀疏。因此，它可以启发研究开发更鲁棒的解码策略。同时，TTFS也作为一种编码方案参与了实验，我们发现这种稀疏编码也可以带来鲁棒性。
SNN有利于在低能量预算的各种边缘设备上实现(Wozniak et al., 2020; Frenkel, 2021)，但现实世界的场景更复杂，需要处理不同规模的输入和不同程度的扰动(Komkov and Petiushko, 2021)。与FGSM攻击相比，仅改变几个像素会产生更复杂和稀疏的扰动(Su et al., 2019)。我们使用数据集来模拟真实图片在不同扰动条件下的结果。SNN能够为各种扰动提供高度鲁棒的解决方案。然而，在所有实验中，我们没有发现SNN配置的特定组合能够提供对扰动的鲁棒性。视觉通路中采用了复杂的编码方案(Webster, 2011)。在我们的实验中，在融合编码下训练的SNN可以补偿各种攻击的鲁棒性，证明了融合编码的必要性和有效性。这些结果有助于解释各种神经编码系统在生物系统中的作用。
目前，我们的实验不包括任何针对扰动的防御措施。我们只是在探索SNN本身使用脉冲时序带来的鲁棒性。缺乏积极的防御措施是我们研究的一个局限。我们目前对SNN的讨论集中在点神经元上，而没有考虑复杂的神经元结构和过程(如突触传导)对精确脉冲时序的影响。这种限制实际上是由SNN训练技术带来的。目前主流的训练方案主要适用于由点神经元构建的SNN。此外，这些训练算法还限制了模拟时间步长的增加，因此SNN在较长时间步长下的鲁棒性仍有待探索。此外，我们主要使用了由ANN获得的黑盒梯度攻击，它是自然可微的。一方面，这是为了考虑实验的公平性。另一方面，针对SNN的攻击方法还不成熟。SNN在这些潜在攻击下的鲁棒性仍然是未来研究的一个悬而未决的问题。我们在这里的工作首次对这个问题进行了系统的研究，为研究SNN的每个组成部分——编码、解码和学习——在下一代大脑启发的计算模型中的作用铺平了道路。
4 Methods
4.1 Neuron and synaptic models
4.2 Encoding and decoding schemes
要将图像输入SNN，首先要考虑输入编码。在这项工作中，我们实现了四种输入编码方案，即Current编码、Poisson编码、Rate-Syn编码和TTFS编码。这里的Current编码表示一种方法，其中图像的浮点像素矩阵被直接馈送到SNN中，持续一些时间步长。在SNN的文献中，它也被称为直接(Direct)编码(Kim et al., 2022)。假设X是图像像素强度，它可以在公式8中公式化。
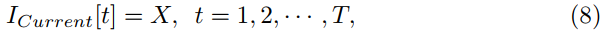
其中T是输入的持续时间。
Poisson编码作为发放率编码最突出的分支，是发放率编码的典型候选者，并处理神经元背景(Amarasingham et al., 2006)。它被广泛应用于SNN领域(Maass and Zador, 1999; Gabbiani and Koch, 1998)。它还首次应用于通过转换将SNN与ANN连接起来(Diehl et al., 2015)，可以在公式9中公式化。
其中Rand(0, 1)是生成均匀分布值的随机生成器，其中每项为0-1范围内的像素矩阵。Poisson编码和Current编码都产生稳定的发放率，被归类为计数率(Count Rate)编码(Auge et al., 2021)。这些方法将像素强度编码为平均发放率。然而，可以观察到，这两种编码方案在鲁棒性方面的增加有限(图1)。
为了打破稳定的瞬时发放率并保持平均发放率，我们开发了Rate-Syn编码方案。Rate-Syn编码是带同步的发放率编码的缩写，我们在这里设计它是为了说明使用典型的发放率编码不足以承载太多的鲁棒性。该编码方案可以用公式10来表示。
由Rate-Syn编码生成的脉冲序列具有同步的结束时间。初次脉冲开始的时间取决于像素值。T步期间的平均发放率近似于Poisson编码和Current编码之一。
除了考虑计数率编码之外，还考虑了基本编码方案——TTFS编码(初次脉冲时间编码)。在TTFS编码中，第一尖峰时间对信息进行编码，可以在等式11中公式化。
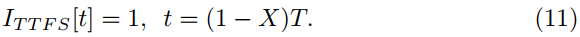
Rate-Syn和TTFS编码之间的区别在于脉冲的数量。TTFS编码在单个脉冲序列中提供一个脉冲，而Rate-Syn自(1−X)T起继续发放。
计数率编码和时序编码代表了从像素值到脉冲序列的两种转换形式。SNN的预测取决于从脉冲序列到数字的操作(或解码)。与编码方法的设计类似，我们在这项工作中使用了两种解码方法，即Rate解码和TTFS解码。Rate解码将脉冲序列转换为平均发放率，而TTFS解码允许多个神经元只关注初次脉冲时间并丢弃发放率信息。解码方法也会影响损失的设计。当训练网络时，解码的向量以真实标签为目标。
4.3 Architectures and Training approaches
对于图1、2、3，为了避免复杂架构带来的鲁棒性影响，我们在全连接网络上进行了实验，对ANN和SNN都没有偏差。我们的实验是在MNIST或Fashion MNIST数据集上进行的。该网络有三个前馈层。输入神经元数为784 (28×28)，与MNIST或Fashion MNIST数据集的图像中的像素数相匹配。该模型输出10个类别的概率进行预测。默认情况下，我们使用平均发放率对SNN输出进行解码。
对于ANN，我们使用反向传播和具有权重衰减的自适应动量估计优化器(AdamW)优化了模型(Loshchilov and Hutter, 2019; Kingma and Ba, 2015)。衰减因子设置为0.01，学习率设置为0.001。用于训练ANN的损失是交叉熵损失，并且该模型在没有进一步指示的情况下训练了100个epoch。
本文考虑了SNN的三种训练方法。它们是基于转换的方法(CVT)、基于激活的反向传播(Act-BP)和基于时序的反向传播(Temp-BP)。对于这里的层 l，我们将突触权重表示为
。
首先，通过对ANN的权值进行转换和重缩放可以获得高精度的SNN。转换的基本原理是将ReLU非线性与IF神经元的发放率相匹配。在脉冲时刻，膜电位
减少等于发放阈值Uth的量，而不是回到静息电位。确切的转换限制了突触后电位的使用，只有脉冲被转移。我们按照Rueckauer等人(2017)提出的方法重新调整了权重。给定ANN中层 l 和l−1的最大激活为max(l)和max(l−1)，权重按公式12缩放。
其中，W(l),SNN是SNN中的转换权重，W(l),ANN是原始ANN权重。基于转换的SNN需要更大的时间步长才能在精度上与原始ANN相媲美。
基于转换的方法不需要通过SNN进行反向传播。已经提出了Act-BP和Temp-BP方法来克服这个问题。这些方法可以使LIF神经元得到更好的训练，因此我们使用Act-BP和Temp-BP来训练LIF神经元的模型。LIF SNN中的层 l 的前向通路可以在公式13中离散化。
其中τs是突触时间常数，H(·)是Heaviside阶跃函数。
对于Act-BP方法，其主要思想是平滑Heaviside阶跃函数。为了做到这一点，我们采用了Neftci等人(2019)中的sigmoid替代函数，使得不可微函数可以具有可用于更新参数的梯度。在前向通路中，网络遵循公式7中的阶跃函数，而在后向通路中它遵循公式14中表示的sigmoid函数。
其中陡度由ρ控制，默认设置为5。
对于Temp-BP方法，Temp-BP方法的关键挑战是如何通过脉冲时间获得
。根据(Zhang and Li, 2020)的研究，我们将分为神经元间和神经元内反向传播。神经元间反向传播发生在突触前发放时间触发突触后电位时。神经元内依赖性定义在任意时间和突触前发放时间之间。
对于SNN，学习率设置为0.0005，还使用AdamW优化器，权重衰减为0.01。所有训练都是使用PyTorch进行的(Paszke et al., 2019)。
在图4中，我们证明了SNN的鲁棒性在更深层次的架构中得以保持，并可应用于真实世界的场景。我们在德国交通标志识别基准(GTSRB)数据集上训练了SNN，该数据集包含43种交通标志的图像。图像的大小首先调整为32×32，有3个通道。然后，我们测试了ReLU和Softplus激活的ANN和LIF神经元的SNN的三种架构。第一种是五层全连接网络(3072-1000-1000-1000-1000-1000-43)。另外两种结构是ResNet18 (He et al., 2016)和VGG9 (Simonyan and Zisserman, 2015)。这两种结构的神经元在SNN中均转变为LIF神经元。为了提高深度网络的泛化能力，我们应用了余弦退火学习率调度。我们还对循环网络进行了比较，即LSTM (Hochreiter and Schmidhuber, 1997)(双向和非双向)和GRU (Cho et al., 2014)。这些循环网络都具有与五层网络相同数量的隐藏神经元。
4.4 Attack methods
本文引用了各种扰动方法来验证其鲁棒性。我们主要关注对现代人工智能构成巨大威胁的对抗攻击。一种类型是基于梯度的攻击方法，需要指定强度的大小。执行攻击的过程是解决公式15中的约束优化问题。
其中，δ是x的扰动，ε是约束δ的p范数的强度，L是网络的损失函数。x∈RN×1，其中N是像素数。我们实现了四种此类方法：快速梯度符号法(FGSM, Goodfellow et al. (2015))、基本迭代法(BIM，Kurakin et al. (2018))、投影梯度下降法(PGD, Madry et al., 2018))和动量迭代法(MIM, Dong et al. (2018))。
FGSM是一种基于梯度的一步方法，可在l∞球内产生攻击：
其中
是相对于x的梯度。MIM通过累积梯度方向上的动量来校准梯度估计，而不是使用直接梯度。
对于BIM和PGD等迭代方法，它们以步长为α的迭代方式解决优化问题。对于l∞迭代攻击，基本迭代可以表示为：
其中k表示迭代步骤的数目。每次迭代中的数据应该投影到关于ε的干净数据x周围的l∞球的空间上。类似地，当涉及到l2迭代攻击时，迭代可以表示为：
其中投影在l2球上。
的初始条件反映了PGD和BIM的巨大差异。BIM使用原始输入作为初始条件：
，而PGD在x中添加高斯噪声作为。在这项工作中，PGD和BIM被投影到l∞和l2球上，以测试其对攻击的鲁棒性。
在foolbox (Rauber et al., 2017)和torchattacks (Kim, 2020)软件包的帮助下，我们对目标模型进行了攻击。在进行攻击时，我们主要采用了黑盒(BB)攻击的设置，考虑到SNN没有自然梯度，黑盒攻击的应用场景更多，攻击者对防御模型一无所知。对于图1、2、3，攻击是从用不同的随机种子训练的ReLU激活的ANN执行的。结构与SNN相同。对于图4，使用ReLU激活的ResNet18执行攻击。图2(J)中也进行了白盒攻击。首先，对于Act-BP和Temp-BP SNN，白盒攻击利用了特殊的反向传播策略，尽管不如ANN反向传播精确。此外，对于基于转换的SNN，这些SNN具有ANN对应物，因此它们可以使用ANN对应物或来自Act-BP的反向传播来执行白盒攻击(Sharmin et al., 2019)。
为了表明不同的训练方法也可以抵抗对时间结构的攻击。我们专门设计了一种随机删除攻击(RandDel)。随机删除丢弃泊松分布脉冲。删除的脉冲与总脉冲的比率为p。通过增加p，可以获得更强的攻击。
最后，为了测试SNN在实际应用场景中的性能，我们还使用了更复杂的对抗策略。这些方法没有可调整的攻击强度，但试图尽可能降低强度并增加扰动的稀疏性，使神经网络给出错误的预测，这可以被形式化为拉格朗日松弛问题：
其中λ控制扰动的正则化。这种扰动方法也称为基于优化的方法。由于目标直接优化扰动的范数，因此扰动更隐蔽，易于操作。我们实现了四种：鲁棒物理扰动(RP2, Eykholt et al. (2018))、DeepFool攻击(Moosavi-Dezbulli et al., 2016)、OnePixel攻击(Su et al., 2019)和FAB攻击(快速自适应边界，Croce and Hein (2020))。对于RP2，我们使用了一个开源的黑盒模型来实现攻击。对于DeepFool、OnePixel和FAB攻击，ReLU激活的ResNet18经过专门训练可以执行攻击。
4.5 Robustness Analysis
在这项工作中，我们使用了两个指标来评估鲁棒性。一个是干净精度的下降。神经网络在受到攻击时可能会给出错误的预测，从而导致精度下降。使用可以调整攻击强度并随着强度的增加显示精度下降的梯度攻击算法，可以很好地表征对抗样本对网络的有害影响。模型越鲁棒，精度下降的幅度就越小。
另一个指标是攻击成功率(ASR)，它衡量对抗样本被模型成功错误分类的概率。在图4中，我们使用攻击成功率来评估不同攻击的效果。对于防御模型来说，较低的攻击成功率意味着更强的鲁棒性。
我们还观察到了网络的其他性质。在用Act-BP或Temp-BP对SNN进行微分后，我们观察到网络相对于扰动的一阶泰勒展开。SNN的一阶泰勒展开式可以表示为(Simon-Gabriel et al., 2019)：
其中h(δ)是高阶多项式的组成。扰动前后损失的变化是标量的，主要受清洁样本的梯度和扰动的影响。因此，我们测量了
。通过微扰方法，较大的意味着损失值的变化较大。
在图3中，我们使用了不同的编码和解码方案来了解它们对SNN鲁棒性的影响。我们表征了由于通过脉冲距离存在扰动而导致的隐层神经元反应的变化。我们使用的距离是Victor-Purpura距离，它根据通过插入、删除和移位将一个脉冲序列转换为另一个脉冲序列的最低成本来测量两个脉冲序列之间的距离(Victor and Purpura, 1997)。
4.6 Simulation details and parameters
Details to: Rate-based SNNs gain robustness through synchronization schemes (Fig. 1).
Details to: Dedicated training algorithms help spiking neural networks to further improve robustness (Fig. 2).
Details to: Diverse combinations of encoding and decoding criteria enhance the robustness of SNNs (Fig. 3).
Details to: Application to real-world scenarios (Fig. 4).
