Optimal ANN-SNN conversion for high-accuracy and ultra-low-latency spiking neural networks
郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
Published as a conference paper at ICLR 2022
ABSTRACT
脉冲神经网络（SNN）因其独特的低功耗属性和对神经形态硬件的快速推理而受到广泛关注。作为获得深度SNN的最有效方法，ANN-SNN转换在大规模数据集上取得了与ANN相当的性能。尽管如此，要使SNN的发放率与ANN的激活相匹配，还需要很长的时间。结果，转换后的SNN在短时间步长下遭受严重的性能退化问题，这阻碍了SNN的实际应用。在本文中，我们从理论上分析了ANN-SNN转换误差，并推导了SNN的估计激活函数。然后，我们提出了量化裁剪-向下取整-移位（quantization clip-floor-shift）激活函数来代替源ANN中的ReLU激活函数，这可以更好地逼近SNN的激活函数。我们证明了SNN和ANN之间的期望转换误差为零，使我们能够实现高精度和超低延迟的SNN。我们在CIFAR-10/100和ImageNet数据集上评估了我们的方法，并表明它在精度和时间步长方面都优于最先进的ANN-SNN和直接训练的SNN。据我们所知，这是首次探索超低延迟（4个时间步长）的高性能ANN-SNN转换。代码位于https://github.com/putshua/SNN_conversion_QCFS。
1 INTRODUCTION
脉冲神经网络（SNN）是基于生物神经元的动态特性的生物学合理的神经网络（McCulloch & Pitts, 1943; Izhikevich, 2003）。作为第三代人工神经网络（Maass, 1997），SNN因其与深度模拟神经网络（ANN）相比具有独特的属性而备受关注（Roy et al., 2019）。当超过阈值时，每个神经元都会发送离散的脉冲信号来传递信息。对于大多数SNN，脉冲神经元将累积最后一层的电流作为推断时间步长T内的输出。二值化激活提供了神经形态计算的专用硬件（Pei et al., 2019; DeBole et al., 2019; Davies et al., 2018）。这种硬件在时间分辨率和能量预算方面具有优异的优势。现有工作显示出巨大的节能潜力，推断速度相当快（Stöckl & Maass, 2021）。
除了效率优势外，SNN的学习算法近年来得到了飞跃性的改进。在大规模数据集上，通过时间反向传播和ANN-SNN转换技术训练的SNN的性能逐渐与ANN相当（Fang et al., 2021; Rueckauer et al., 2017）。这两种技术都得益于SNN推断时间的设置。在反向传播中设置更长的时间步骤可以使替代函数的梯度更可靠（Wu et al., 2018; Neftci et al., 2019; Zenke & Vogels, 2021）。然而，代价是训练期间的巨大资源消耗。基于CUDA的TensorFlow和PyTorch等现有平台对SNN训练的优化有限。相比之下，ANN-SNN转换通常取决于更长的推理时间，以获得与原始ANN相当的精度（Sengupta et al., 2019），因为它基于ReLU激活和IF模型的发放率的等效性（Cao et al., 2015）。虽然更长的推理时间可以进一步减少转换误差，但这也阻碍了SNN在神经形态芯片上的实际应用。
ANN-SNN转换的困境在于，转换理论中存在剩余的潜力，很难在几个时间步骤内消除（Rueckauer et al., 2016）。尽管已经提出了许多方法来提高转换精度，例如权重归一化（Diehl et al., 2015）、阈值重新缩放（Sengupta et al., 2019）、软重置（Han & Roy, 2020）和阈值偏移（Deng & Gu, 2020），但基准工作中的数十到数百个时间步骤仍然无法承受。为了获得具有超低延迟（例如，4个时间步骤）的高性能SNN，我们列出了ANN-SNN转换中的关键误差，并为每个误差提供了解决方案。我们的主要贡献总结如下：
- 我们深入研究了ANN-SNN转换中的误差，并将其归因于裁剪误差、量化误差和不均匀性误差。我们发现，由到达脉冲的时间变化引起的不均匀误差（在以前的工作中被忽略）可以如预期的那样导致更多的脉冲或更少的脉冲。
- 我们提出了量化裁剪-向下取整-移位激活函数来代替源ANN中的ReLU激活函数，这更好地逼近了SNN的激活函数。我们证明了SNN和ANN之间的预期转换误差为零，表明我们可以在超低时间步长下实现高性能的转换SNN。
- 我们在CIFAR-10、CIFAR-100和ImageNet数据集上评估了我们的方法。与ANN-SNN转换和反向传播训练方法相比，所提出的方法以更少的时间步长超过了最先进的精度。例如，我们在CIFAR-10上以前所未有的2个时间步长达到了91.18%的最高精度。
2 PRELIMINARIES
在本节中，我们首先简要回顾了SNN和ANN的神经元模型。然后介绍了ANN-SNN转换的基本框架。
Neuron model for ANNs. 对于ANN，模拟神经元的计算可以简化为线性变换和非线性映射的组合：
其中向量al表示第 l 层中所有神经元的输出，Wl表示第 l 和第l−1层之间的权重矩阵，h(·)表示ReLU激活函数。
Neuron model for SNNs. 与之前的工作类似（Cao et al., 2015; Diehl et al., 2015; Han et al., 2020），我们考虑了SNN的IF模型。如果第 l 层的IF神经元接收到来自最后一层的输入xl−1(t)，则IF神经元的时间电位可以定义为：
其中ml(t)和vl(t)表示在时间步骤 t 发放脉冲之前和之后的膜电位。Wl表示第 l 层中的权重。一旦ml(t)的任何元素
超过发放阈值θl，神经元将引发脉冲并更新膜电位
。为了避免信息丢失，我们使用了“减法重置”机制（Rueckauer et al., 2017; Han et al., 2020），而不是“重置为零”机制，这意味着如果神经元发放，则用阈值θl减去膜电位。基于上文讨论的阈值触发发放机制和发放后膜电位的“减法重置”，我们可以将膜电位的更新规则写为：
这里sl(t)指的是层 l 中所有神经元在时刻 t 的输出脉冲，如果有脉冲，其元素等于1，否则为0。H(·)是Heaviside阶跃函数。θl是发放阈值θl的矢量。与Deng & Gu（2020）类似，我们假设如果第l−1层中的突触前神经元发放脉冲，则第 l 层中的突触后神经元接收未加权的突触后电位θl，即：
ANN-SNN conversion. ANN-SNN转换的关键思想是将ANN中模拟神经元的激活值映射到SNN中脉冲神经元的发放率（或平均突触后电位）。具体而言，我们可以通过组合公式2–公式4来获得潜在更新公式：
公式6描述了ANN-SNN转换中使用的脉冲神经元的基本函数。通过将公式6从时间1到T求和，并在两边除以T，我们得到：
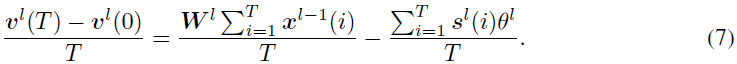
如果我们使用
表示从0到T期间的平均突触后电位，并将公式5代入公式7，则我们得到：
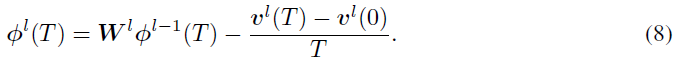
公式8描述了相邻层神经元的平均突触后电位的关系。注意，
。如果我们将初始电势vl(0)设置为零，并且当模拟时间步长T足够长时忽略剩余项
，则转换后的SNN具有与源ANN几乎相同的激活函数（公式1）。然而，高T值会导致长的推理延迟，从而阻碍SNN的实际应用。因此，本文旨在实现具有极低延迟的高性能ANN-SNN转换。
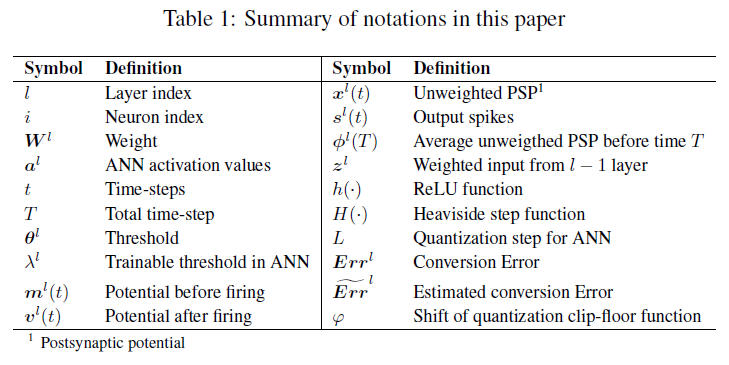
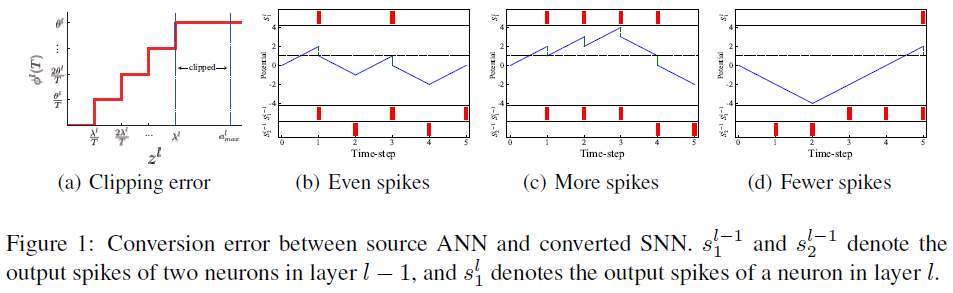
3 CONVERSION ERROR ANALYSIS
在本节中，我们将详细分析每个层中源ANN和转换SNN之间的转换误差。在下文中，我们假设ANN和SNN都从层l−1接收相同的输入，即al−1 = Φl−1(T)，然后分析层 l 中的误差。绝对转换误差正好是转换SNN的输出减去ANN的输出：
其中h(zl) = ReLU(zl)。从公式9可以发现，如果vl(T) − vl(0) ≠ 0且zl > 0，则转换误差为非零。事实上，转换误差是由三个因素造成的。
Clipping error. SNN的输出Φl(T)在[0, θl]的范围内，因为
（见公式5）。然而，ANN的输出al在更大范围内（[0, 
]），其中表示al的最大值。如图1a所示，al可以通过以下公式映射到Φl(T)：
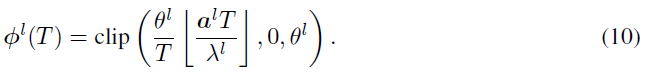
这里，clip函数设置上界θl和下界0。⌊·⌋表示向下取整函数。λl表示输出al的实际最大值，映射到Φl(T)的最大值θl。考虑到ANN中近99.9%的al激活率在[0, 
]的范围内，Rueckauer等人（2016）建议根据99.9%的激活率选择λl。ANN中λl和之间的激活被映射到SNN中的相同值θl，这将导致称为裁剪误差的转换误差。
Quantization error (flooring error). 输出脉冲sl(t)是离散事件，因此，Φl(T)是离散的，量化分辨率为
（见公式10）。当将al映射到Φl(T)时，存在不可避免的量化误差。例如，如图1a所示，在
范围内的ANN激活被映射到SNN的相同值。
Unevenness error. 不均匀性误差是由输入脉冲的不均匀性引起的。如果到达脉冲的时间发生变化，则输出发放率可能发生变化，从而导致转换误差。有两种情况：预期的脉冲更多或预期的脉冲更少。为了看到这一点，在源ANN中，我们假设l−1层中的两个模拟神经元连接到 l 层中的一个模拟神经元，权重为2和-2，并且l−1层中神经元的输出向量al−1为[0.6, 0.4]。此外，在转换的SNN中，我们假定l−1层的两个脉冲神经元在5个时间步骤（T=5）内分别发放3个脉冲和2个脉冲，并且阈值θl−1=1。因此，
=[0.6, 0.4]。尽管Φl-1(T) = al−1并且ANN和SNN的权重相同，但如果到达脉冲的时间发生变化，则Φl(T)可能与al不同。根据公式1，ANN输出al = Wlal−1 = [2, −2][0.6, 0.4]T = 0.4。对于SNN，假设阈值θl=1，有三种可能的输出发放率，如图1(b)-(d)所示。如果两个突触前神经元分别在t=1, 3, 5和t=2, 4（红条）处发放，权重为2和-2，则突触后神经元将在t=1, 3（红条）处发放两个脉冲，并且
。然而，如果突触前神经元分别在t=1, 2, 3和t=4, 5时发放，则突触后神经元将在t=1, 2, 3, 4时发放四个脉冲，并且Φl(T) = 0.8 > al。如果突触后神经元分别在t=3, 4, 5和t=1, 2中发放，则突触后神经将在t=5时仅发放一个脉冲，并且Φl(T) = 0.2 < al。
注意，Li等人（2021）提出了裁剪误差和量化误差。上述三种误差之间存在相互依存关系。具体而言，如果vl(T)在[0, θl]的范围内，则不均匀误差将退化为量化误差。假设电势vl(T)落入[0, θl]将使我们能够估计SNN的激活函数，忽略不均匀误差的影响。因此，转换后的SNN中的输出值Φl(T)的估计可以通过裁剪函数和向下取整函数的组合来公式化，即：
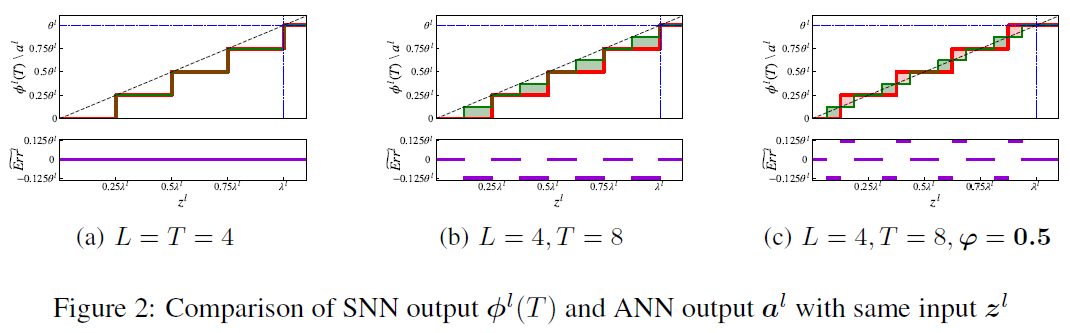
详细推导见附录。借助于对SNN输出的这种估计，可以从公式9导出估计的转换误差
：
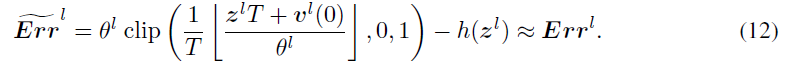
4 OPTIMAL ANN-SNN CONVERSION
4.1 QUANTIZATION CLIP-FLOOR ACTIVATION FUNCTION
根据公式12的转换误差，很自然地认为，如果将常用的ReLU激活函数h(zl)替换为具有给定量化步长L的裁剪-向下取整函数（类似于公式11），则将消除时间步骤T＝L处的转换误差。因此，低延迟时的性能下降问题将得到解决。如公式13所示，我们提出了量化裁剪-向下取整激活函数来训练ANN。
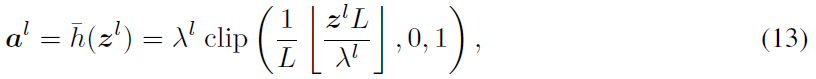
其中，超参数L表示ANN的量化步长，可训练λl决定了ANN中al的最大值，映射到SNN中的Φl(T)的最大值。请注意，zl = WlΦl-1(T) = Wlal−1。利用这个新的激活函数，我们可以证明SNN和ANN之间估计的转换误差为零，并且我们有以下定理。
定理1表明，如果转换后的SNN的时间步长T与源ANN的量化步长L相同，则转换误差将为零。一个例子如图2a所示，其中T=L=4，θl = λl。红色曲线表示对应于不同输入zl的转换SNN的估计输出Φl(T)，而绿色曲线表示对应于不同输入zl的源ANN的输出。由于这两条曲线相同，因此估计的转换误差为零。然而，在实际应用中，我们关注的是SNN在不同时间步长的性能。当T不等于L时，不能保证转换误差为零。如图2b所示，其中L=4和L=8，我们可以发现一些zl的转换误差大于零。该误差将逐层传输，并最终降低转换后的SNN的精度。解决这个问题的一种方法是训练具有不同量化步长的多个源ANN，然后将它们转换为具有不同时间步长的SNN，但这需要付出相当大的代价。在下一节中，我们提出了带有移位项的量化裁剪-向下取整激活函数来解决这个问题。这种方法可以在没有额外计算成本的情况下实现不同时间步长的高精度。
4.2 QUANTIZATION CLIP-FLOOR-SHIFT ACTIVATION FUNCTION
我们提出了量化裁剪-向下取整-移位激活函数来训练神经网络。
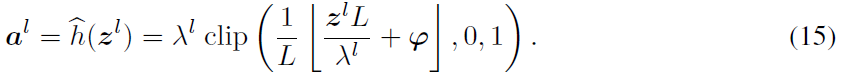
与公式13相比，存在控制激活函数移位的超参数向量φ。当L≠T时，我们不能保证转换误差为0。然而，我们可以估计转换误差的预期。类似于（Deng & Gu，2020），我们假设当t = 1, 2, … , T，l = 1, 2, ... , L时，
在区间[(t - 1)λl / T, tλl / T]和[(l - 1)λl / L, lλl / L]内均匀分布，我们有以下定理。
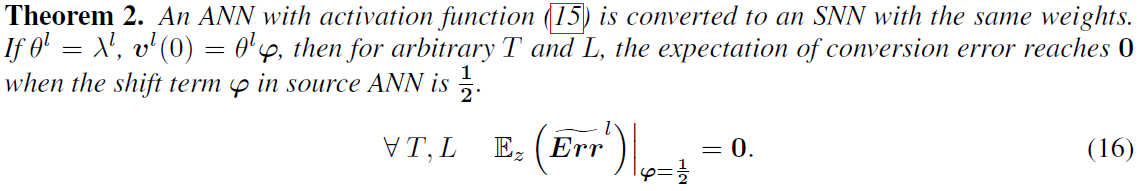
证据在附录中。定理2表明，移位项1/2能够优化对转换误差的期望。通过比较图2b和图2c，我们可以发现，当添加移位项φ=0.5时，即使L ≠ T，平均转换误差也达到零。这些结果表明，我们可以在超低时间步长下实现高性能的转换SNN。
L是量化裁剪-向下取整-移位激活的唯一未确定的超参数。当T＝L时，转换误差达到零。因此，我们自然认为应该将参数L设置得尽可能小，以便在较低的时间步长下获得更好的性能。然而，当时间步长相对较小时，激活函数的量化过低将降低模型容量，并进一步导致精度损失。选择合适的L是SNN在低延迟时的准确性和最优准确性之间的权衡。我们将在实验部分进一步分析量化步长L的影响。
4.3 ALGORITHM FOR TRAINING QUANTIZATION CLIP-FLOOR-SHIFT ACTIVATION FUNCTION
用量化裁剪-向下取整-移位激活而不是ReLU来训练ANN也是一个难题。为了直接训练ANN，我们使用直通估计器（Bengio et al.，2013）来计算截断函数的导数，即d⌊x⌋/dx = 1。公式17给出了总体推导规则。
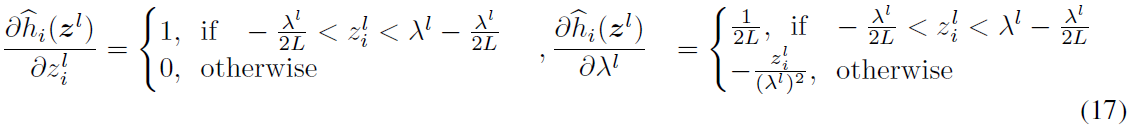
这里
是zl的第 i 个元素。然后，我们可以使用随机梯度下降算法（Bottou，2012），通过量化裁剪-向下取整-移位激活来训练ANN。
5 RELATED WORK
Cao等人（2015）首次启动了对ANN-SNN转换的研究。然后Diehl等人（2015）使用基于数据和基于模型的归一化将三层CNN转换为SNN。为了获得复杂数据集和深层网络的高性能SNN，Rueckauer等人（2016）和Sengupta等人（2019）提出了更精确的缩放方法，分别对权重和阈值进行归一化，后来证明这两种方法是等效的（Ding等人，2021）。然而，由于第3节中分析的转换误差，转换后的深度SNN需要数百个时间步骤才能获得准确的结果。为了解决潜在的信息损失，Rueckauer等人（2016）和Han等人（2020）建议使用“减法重置”神经元，而不是“重置为零”神经元。最近，已经提出了许多方法来消除转换误差。Rueckauer等人（2016）建议99.9%的激活作为比例因子，Ho & Chang（2020）添加了可训练的裁剪层。此外，Han等人（2020）重新调整了SNN阈值，以避免脉冲神经元的不当激活。Massa等人（2020）和Singh等人（2021）评估了转换后的SNN在Loihi神经形态处理器上的性能。我们的工作与Deng & Gu（2020）有相似之处；Li等人（2021）也阐明了转换误差。Deng & Gu（2020）通过在转换的SNN偏差之外引入额外的偏差，将逐层误差降至最低。Li等人（2021）进一步建议使用量化微调校准权重和偏差。他们以16个和32个时间步骤获得了良好的结果，在更极端的时间步长中没有踪迹。相比之下，我们的工作旨在通过消除上述转换误差的技术将人工神经网络融入SNN。实现量化层的端到端训练以获得更好的整体性能。我们的偏移校正可以使得单个SNN在超低和大时间步长下都表现良好。即使对于像时间反向传播（BPTT）这样的监督学习方法，也很难在极少数的时间步长内保持SNN性能。由于全面的训练，BPTT通常需要较少的时间步长，但以大量GPU计算为代价（Wu et al., 2018; 2019; Lee et al., 2016; Neftci et al., 2019; Lee et al., 2020; Zenke & Vogels, 2021）。基于时间的反向传播方法（Bohte et al., 2002; Tavanei et al., 2019; Kim et al., 2020）可以在很短的时间窗口内训练SNN，例如在5-10个时间步骤内。然而，它们通常局限于简单的数据集，如MNIST（Kheradpisheh & Masquelier, 2020）和CIFAR10（Zhang & Li, 2020）。Rathi等人（2019）通过使用转换方法初始化SNN，然后使用STDP调整SNN，缩短了模拟步长。在本文中，所提出的方法实现了具有超低延迟（4个时间步骤）的高性能SNN。
6 EXPERIMENTS
在本节中，我们验证了我们的方法的有效性，并将我们的方法与其他最先进的方法在CIFAR-10（LeCun et al., 1998）、CIFAR100（Krizhevsky et al., 2009）和ImageNet数据集（Deng et al., 2009）上进行图像分类任务的比较。与之前的工作类似，我们使用VGG-16（Simonyan & Zisserman, 2014）、ResNet-18（He et al., 2016）和ResNet-20网络结构作为源ANN。我们将我们的方法与最先进的ANN-SNN转换方法进行了比较，其中包括Rathi等人（2019）的Hybrid-Conversion（HC）、Han等人（2020）的RMP、Han和Roy（2020）的TSC、Ding等人（2021）的RNL、Deng和Gu等人（2020）的ReLUThresholdShift（RTS）以及Li等人（2021）的高级流水线SNN转换（SNNC-AP）。还包括与不同SNN训练方法的比较，以表明低延迟推理的优越性，包括Rathi等人的HybridConversion-STDB（HC-STDB）（2019），Wu等人（2018）的STBP，Wu等人（2019）的DirectTraining（DT），Zhang和Li（2020）的TSSL。附录中提供了所提出的ANN-SNN算法和训练配置的详细信息。
6.1 TEST ACCURACY OF ANN WITH QUANTIZATION CLIP-FLOOR-SHIFT ACTIVATION
我们首先比较了具有量化裁剪-向下取整激活的ANN（绿色曲线）、具有量化裁剪-向下取整-移位激活的ANN（蓝色曲线）和具有ReLU激活的原始ANN（黑色虚线）的性能。图3(a)-(d)报告了CIFAR-10上的VGG-16、CIFAR-10的ResNet-20、CIFAR-100上的VGG-16和CIFAR-100的ResNet20的结果。具有量化裁剪-向下取整-移位激活的ANN的性能优于具有量化裁剪-向下取整激活的人工网络。当L>4时，这两个ANN可以实现与具有ReLU激活的原始ANN相同的性能。这些结果表明，我们的量化裁剪-向下取整-移位激活函数几乎不会影响ANN的性能。
6.2 COMPARISON WITH THE STATE-OF-THE-ART
表2将我们的方法与CIFAR-10上最先进的ANN-SNN转换方法进行了比较。对于低延迟推理（T≤64），我们的模型在相同的时间步长设置下优于所有其他方法。对于T=32，我们的方法的准确性略好于ANN（95.54% vs. 95.52%），而RMP、RTS、RNL和SNNC-AP方法的准确性损失分别为33.3%、19.48%、7.42%和2.01%。此外，我们仅使用4个时间步骤就实现了93.96%的准确性，这比使用32个时间步骤的SNNC-AP快8倍。对于ResNet-20，我们在4个时间步骤内实现了83.75%的准确率。值得注意的是，我们的超低延迟性能与其他最先进的监督训练方法相当，如附录的表S3所示。
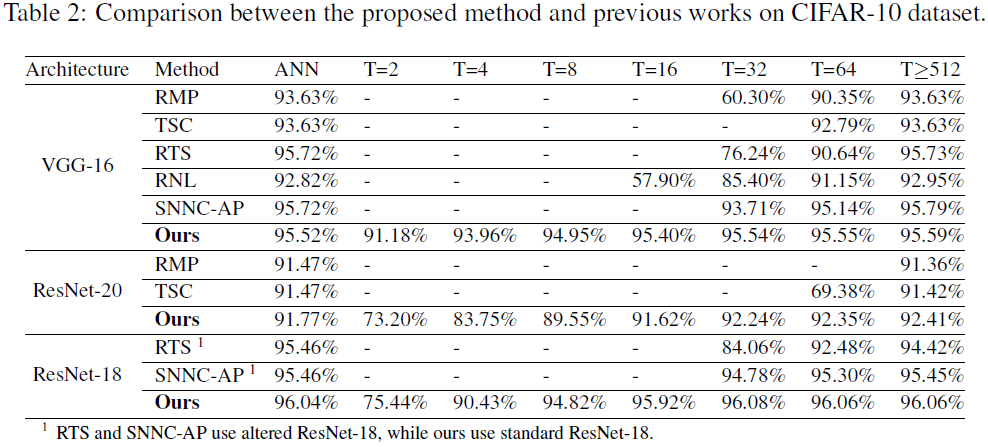
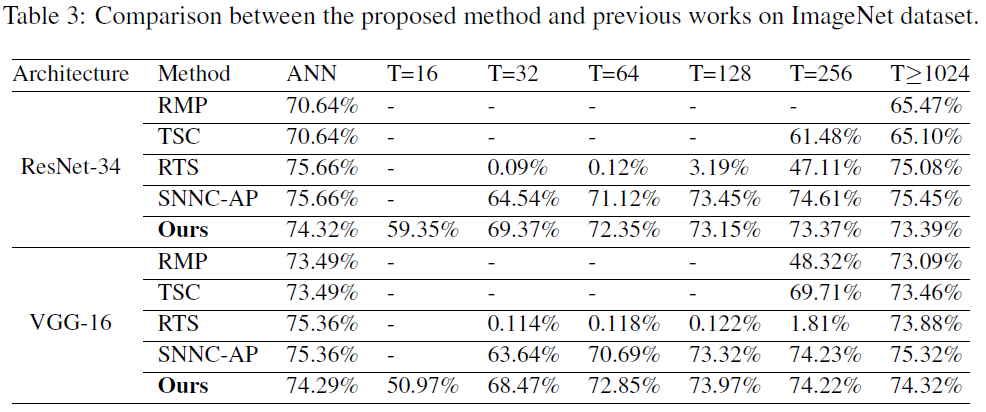
我们在大规模数据集上进一步测试了我们的方法的性能。表3在ImageNet上报告了结果，我们的方法在高精度和超低延迟方面也优于其他方法。对于ResNet-34，当T=32时，所提出的方法的准确度比SNNC-AP高4.83%，比RTS高69.28%。当时间步长为16时，我们仍然可以达到59.35%的精度。对于VGG-16，当T=32时，所提出的方法的精度比SNNC-AP高4.83%，比RTS高68.356%。当时间步长为16时，我们仍然可以达到50.97%的准确率。这些结果表明，我们的方法优于以前的转换方法。关于CIFAR-100的更多实验结果见附录表S4。
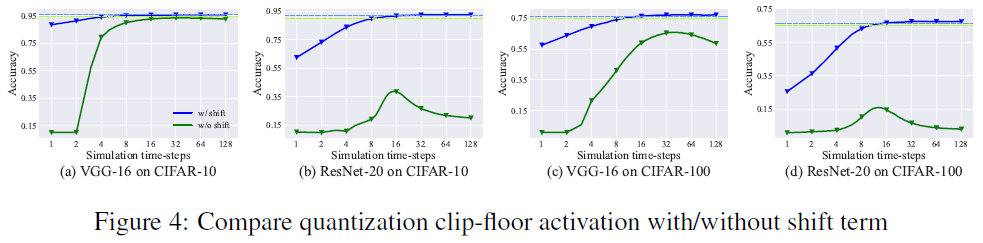
6.3 COMPARISON OF QUANTIZATION CLIP-FLOOR AND QUANTIZATION CLIP-FLOOR-SHIFT
在这里，我们进一步比较了从具有量化裁剪-向下取整激活的ANN和具有量化裁剪-向下取整-移位激活的ANN转换而来的SNN的性能。在第4节中，我们证明了无论T和L是否相同，在量化裁剪-向下取整-移位激活的情况下，转换误差的期望值都达到0。为了验证这些，我们将L设置为4，并分别使用量化裁剪-向下取整激活和量化裁剪-向下取整-移位激活来训练ANN。图4显示了转换后的SNN的精度如何随时间步长T而变化。来自具有量化裁剪-向下取整激活的ANN（绿色虚线）的转换后SNN（绿色曲线）的精度首先随着时间步长的增加而增加，然后迅速降低，因为当T不等于L时，我们不能保证转换误差为零。最佳性能仍然低于源ANN（绿色虚线）。相反，从具有量化裁剪-向下取整-移位激活的ANN转换的SNN的精度（蓝色曲线）随着T的增加而增加。当时间步长大于16时，它获得与源ANN（蓝色虚线）相同的精度。
6.4 EFFECT OF QUANTIZATION STEPS L
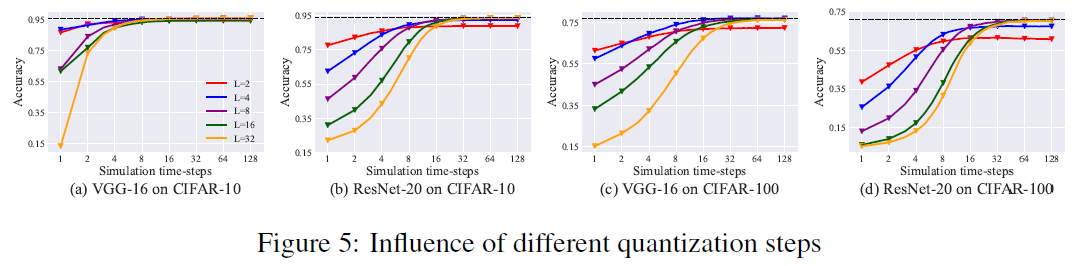
在我们的方法中，量化步长L是一个超参数，它会影响转换后的SNN的准确性。为了分析L的影响并更好地确定最优值，我们使用不同的量化步骤L（包括2，4，8，16和32）训练VGG16/ResNet-20网络，并将其转换为SNN。CIFAR-10/100数据集的实验结果如表S2和图5所示，其中黑色虚线表示ANN的精度，彩色曲线表示转换后的SNN的精度。为了平衡低延迟和高精度之间的权衡，我们主要从两个方面评估转换后的SNN的性能。首先，我们关注超低延迟（4个时间步骤内）下的SNN准确性。其次，我们考虑SNN的最佳准确性。可以明显地发现，超低延迟下的SNN准确性随着L的增加而降低。然而，过小的L将降低模型容量，并进一步导致精度损失。当L=2时，SNN的最佳精度与源ANN之间存在明显差距。当L>4时，SNN的最佳精度接近源ANN。总之，参数L的设置主要取决于低延迟或最佳准确性的目标。推荐的量化步长L是4或8，这导致在小的时间步长和非常大的时间步长下的高性能转换SNN。
7 DISCUSSION AND CONCLUSION
在本文中，我们提出了ANN-SNN转换方法，实现了高精度和超低延迟的深度SNN。我们提出了量化裁剪-向下取整-移位激活来代替ReLU激活，这几乎不影响ANN的性能，并且更接近SNN激活。此外，我们证明了预期的转换误差为零，无论SNN的时间步长和ANN的量化步长是否相同。我们在CIFAR-10、CIFAR-100和ImageNet数据集上以更少的时间步长实现了最先进的精度。我们的研究结果有利于神经形态硬件的实现，并为SNN的大规模应用铺平道路。
Deng & Gu（2020）的工作增加了转换后的SNN的偏差，以偏移理论ANN-SNN曲线，从而使量化误差最小化，与此不同，我们在量化裁剪-向下取整激活函数中添加了移位项，并使用该量化裁剪-向下取整-移位函数来训练源ANN。我们表明，当时间步长和量化步长不匹配时，移位项可以克服性能退化问题。由于不均匀误差，即使当L=T时，ANN精度和SNN精度之间仍然存在差距。此外，当时间步长T=1时，很难实现高性能的ANN-SNN转换。所有这些问题都值得进一步研究。基于转换的方法的一个优点是，它们可以降低总体计算成本，同时保持与源ANN相当的性能。将基于转换的方式与模型压缩相结合，可以显著降低神经元活动，从而减少能耗，而不会损失准确性（Kundu et al., 2021; Rathi & Roy, 2021），这是一个很有希望的方向。
A APPENDIX
A.1 NETWORK STRUCTURE AND TRAINING CONFIGURATIONS
在训练ANN之前，我们首先将最大池化替换为平均池化，然后将ReLU激活替换为所提出的量化裁剪-向下取整-移位激活（公式15）。训练后，我们将所有权重从源ANN复制到转换后的SNN，并将转换后的SN的每一层中的阈值θl设置为等于同一层中源ANN的最大激活值λl。此外，我们将转换后的SNN中的初始膜电位vl(0)设置为θl/2，以匹配源ANN中量化裁剪-向下取整-移位的最优位移φ=1/2。
尽管有常见的数据归一化，但我们使用了一些数据预处理技术。对于CIFAR数据集，我们将图像大小调整为32×32，而对于ImageNet数据集，则将图像大小重新调整为224×224。此外，我们对所有数据集使用随机裁剪图像、Cutout（DeVries & Taylor, 2017）和AutoAugment（Cubuk et al., 2019）。
我们使用动量参数为0.9的随机梯度下降优化器（Bottou, 2012）。对于CIFAR-10和ImageNet，初始学习率设置为0.1，对于CIFAR-100，初始学习速率设置为0.02。余弦衰减调度器（Loshchilov & Hutter, 2016）用于调整学习速率。我们对CIFAR数据集应用权重衰减5×10-4，而对ImageNet应用权重衰减1×10-4。我们为300个epoch训练所有模型。当在CIFAR-10数据集上训练所有网络时，量化步长L被设置为4，并且在CIFAR-100数据集中训练VGG-16、ResNet-18。在CIFAR-100上训练ResNet-20时，参数L设置为8。在ImageNet上训练ResNet-34和VGG-16时，参数L分别设置为8、16。我们在评估转换后的SNN时使用恒定输入。
A.2 INTRODUCTION OF DATASETS
CIFAR-10. CIFAR-10数据集（Krizhevsky et al., 2009）由10个类别的60000个32×32的图像组成。有50000个训练图像和10000个测试图像。
CIFAR-100. CIFAR-100数据集（Krizhevsky et al., 2009）由100个类别的60000个32×32的图像组成。有50000个训练图像和10000个测试图像。
ImageNet. 我们使用ILSVRC 2012数据集（Russakovsky et al., 2015），该数据集由1281167张训练图像和50000张测试图像组成。
A.3 DERIVATION OF EQUATION 12 AND PROOF OF THEOREM 2
Derivation of Equation 11
类似于zl = Wlal−1，我们定义：
我们使用
和
分别表示向量ul(t)和zl中的第 i 个元素和。为了推导公式11，需要对ANN激活值和SNN突触后电位之间的关系进行一些额外的假设，如公式S2所示。
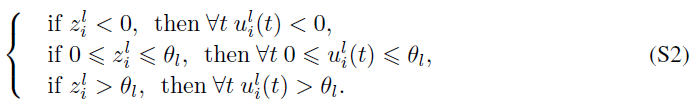
根据上述假设，我们可以讨论神经元在每个时间步骤的发放行为。当
或
时，神经元将在所有时间步骤不发放或发放，这意味着
或
。在这种情况下，我们可以使用一个clip函数来表示
。
当
时，SNN中突触前神经元的每个输入都落入[0, θl]，则我们有
。我们可以将公式8改写为以下公式。
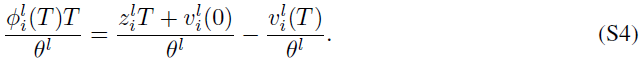
考虑到
和
，公式S4改为：
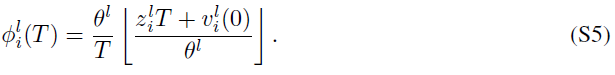
我们将这两种情况（公式S3和公式S4）结合起来，得出：
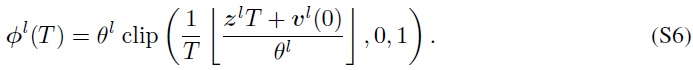
Proof of Theorem 2
在证明定理2之前，我们首先引入引理1。
A.4 COMPARISON OF THE METHODS WITH OR WITHOUT DYNAMIC THRESHOLD ON THE CIFAR-100 DATASET
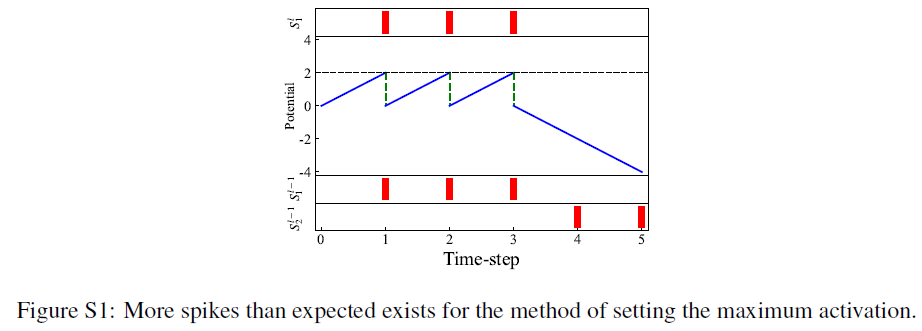
在本文中，我们使用训练参数λl来确定神经网络激活的最大值。先前的工作建议将训练后神经网络激活的最大值设置为阈值。如果我们设置
，比预期出现的脉冲少的情况从未发生，因为我们可以证明vl(T) < θl（见定理3）。尽管如此，仍存在比预期出现的脉冲多的情况。图S1中给出了一个例子。在这里，我们考虑与图1中相同的示例。在源ANN中，我们假设l−1层中的两个模拟神经元连接到 l 层中的一个模拟神经元，权重为2和-2，并且l−1层中神经元的输出向量al−1为[0.6, 0.4]。此外，在转换SNN中，我们假定l−1的两个脉冲神经元在5个时间步骤（T=5）内分别发放3个脉冲和2个脉冲，阈值θl−1=1。因此，
。根据公式1，ANN输出al = Wlal−1 = [2, −2][0.6，0.4]T = 0.4。至于SNN，我们假设突触前神经元分别在t=1, 2, 3和t=4, 5时发放。即使我们将阈值θl=1设置为最大激活2，突触后神经元也会在t=1, 2, 3时发出三个脉冲，并且Φl(T) = 0.6 > al。
此外，设置
作为阈值带来了另外两个问题。首先，由于大阈值，脉冲神经元需要很长时间才能发放脉冲，这使得很难在几个时间步骤内保持SNN的性能。其次，量化误差将很大，因为它与阈值成比例。如果一层的转换误差不为零，它将逐层传播，并将被更大的量化误差放大。我们比较了我们的方法和在CIFAR-100数据集上设置最大激活的方法。结果如表S1所示，其中DT表示我们方法中的动态阈值。结果表明，我们的方法可以获得更好的性能。
A.5 EFFECT OF QUANTIZATION STEPS L
A.6 COMPARISON WITH STATE-OF-THE-ART SUPERVISED TRAINING METHODS ON CIFAR-10 DATASET
A.7 COMPARISON ON CIFAR-100 DATASET
A.8 ENERGY CONSUMPTION ANALYSIS
A.9 PSEUDO-CODE FOR OVERALL CONVERSION ALGORITHM
