Spatio-Temporal Backpropagation for Training High-performance Spiking Neural Networks

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布

FRONTIERS IN NEUROSCIENCE, (2018)

 

Abstract

　　与人工神经网络(ANN)相比，脉冲神经网络(SNN)有望探索类脑行为，因为脉冲可以编码更多时空信息。尽管现有的包括ANN预训练或基于反向传播(BP)的直接训练方案使SNN的监督训练成为可能，但这些方法仅利用网络的空间域信息导致性能瓶颈，并且需要许多复杂的训练技术。另一个基本问题是脉冲活动自然是不可微的，这给训练SNN带来了很大的困难。为此，我们构建了一个对梯度下降训练更友好的迭代LIF模型。通过在训练阶段同时考虑逐层空间域(SD)和时序相关时间域(TD)，以及脉冲活动的近似导数，我们提出了时空反向传播(STBP)的训练框架，不使用任何复杂技能。我们设计了相应的全连接和卷积架构，并在静态MNIST和自定义对象检测数据集以及动态N-MNIST上评估我们的框架。结果表明，与脉冲网络上现有的最先进算法相比，我们的方法实现了最优精度。这项工作为探索具有丰富时空动态的未来类脑计算范式的高性能SNN提供了新的视角。

 

I. INTRODUCTION

　　深度神经网络(DNN)在不同领域取得了出色的表现[1]-[5]，而大脑似乎使用了另一种网络架构，脉冲神经网络，来实现各种复杂的认知功能[6]-[8]。与现有的DNN相比，SNN主要有两个优势：1）流经SNN的脉冲模式从根本上编码了更多的时空信息，而大多数DNN缺乏时序动态，尤其是广泛使用的前馈DNN；2）SNN的事件驱动范式可以使其对硬件更加友好，并被许多神经形态平台采用[9]-[14]。

　　然而，由于脉冲活动的非常复杂的动态和不可微的性质，它在训练SNN方面仍然具有挑战性。综上所述，SNN的训练方法有以下三种：1）无监督学习；2）间接监督学习；3）直接监督学习。第一个起源于权重改变的生物突触可塑性，例如脉冲时序依赖可塑性(STDP)[15]-[17]。因为它只考虑局部神经元活动，很难达到高性能。第二个首先训练一个ANN，然后将其转换为具有相同网络结构的SNN版本，其中SNN神经元的发放率充当ANN神经元的模拟活动[18]-[21]。这不是探索SNN学习性质的生物可行方式。获得高性能训练的最有前途的方法是最近基于梯度下降理论和误差反向传播的直接监督学习。然而，这种方法只考虑了逐层空间域，而忽略了时域中的动态[22][23]。因此，需要许多复杂的训练技能来提高性能[19][23][24]，例如固定数量比例重置、横向抑制、误差归一化、权重/阈值正则化等。因此，非常需要一个关于SNN的更通用的动态模型和学习框架。

　　在本文中，我们为SNN提出了一个直接监督学习框架，它在训练阶段结合了SD和TD。首先，我们构建了一个具有SNN动力学的迭代LIF模型，但它对梯度下降训练很友好。然后我们在误差反向传播过程中同时考虑空间方向和时间方向，即时空反向传播(STBP)，这显著提高了网络精度。此外，我们引入了一个近似导数来解决脉冲活动的不可微分问题。我们通过在静态MNIST和自定义对象检测数据集以及动态N-MNIST上使用全连接和卷积架构来测试我们的SNN框架。由于我们提出的方法可以充分利用捕捉SNN性质的STD信息，因此可以避免现有方案通常需要的许多复杂的训练技能。实验结果表明，与现有的最先进算法相比，我们提出的方法可以在静态或动态数据集上实现最佳精度。系统地分析了TD动态的影响和不同的微分逼近方法。这项工作将为探索具有丰富STD动态的未来类脑计算范式的高性能SNN开辟道路。

 

II. METHOD AND MATERIAL

A. Iterative Leaky Integrate-and-Fire Model in Spiking Neural Networks

　　与现有的深度神经网络相比，脉冲神经网络从根本上编码了更多的时空信息，原因有两个：i）SNN也可以具有像DNN一样的深层架构，以及ii）每个神经元都有自己的神经元动态特性。前一种赋予SNN丰富的空间域信息，而后一种赋予SNN编码时域信息的能力。然而，目前还没有统一的框架允许通过考虑时空动态来有效训练SNN，就像在DNN中实现反向传播(BP)一样。这对SNN在各种应用中的广泛使用提出了挑战。在这项工作中，我们将提出一个基于迭代LIF模型的框架，使我们能够应用时空反向传播来训练脉冲神经网络。

　　众所周知，LIF是描述SNN中神经元动态的最广泛应用的模型，它可以简单地由下式表示：

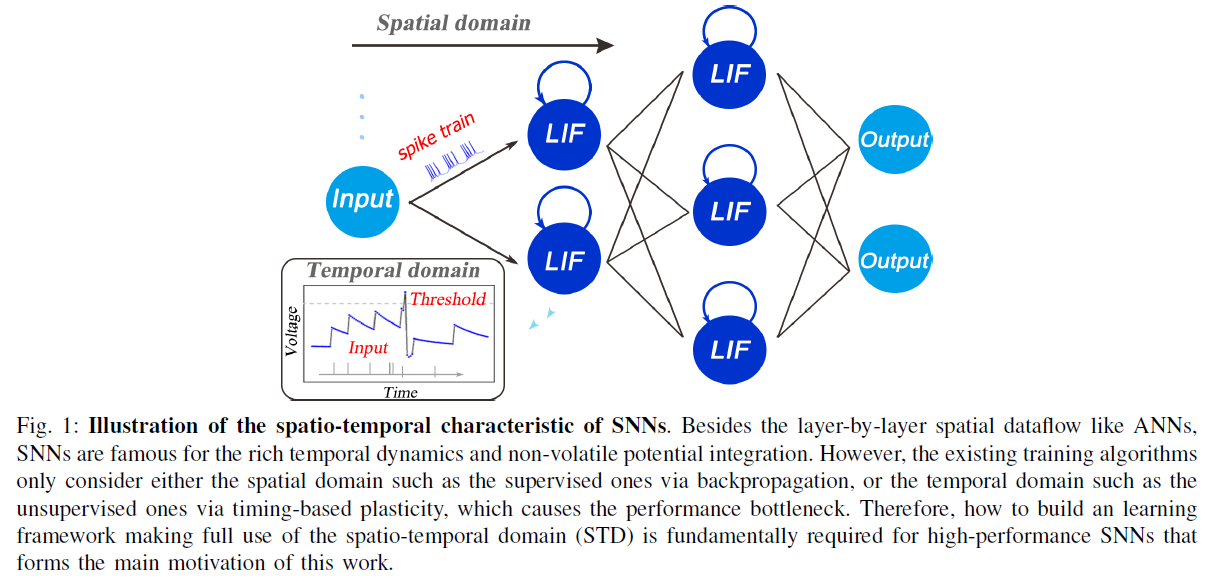
其中u(t)是时间 t 的神经元膜电位，τ是时间常数，I(t)表示由前神经元活动或外部注射和突触权重决定的突触前输入。当膜电位u超过给定的阈值V_th时，神经元会触发脉冲并将其电位重置为u_reset。如图1所示，SNN的前向数据流像DNN一样在逐层SD中传播，每个神经元节点的自反馈注入在TD中生成非易失性集成。通过这种方式，整个SNN以复杂的STD动态运行，并将时空信息编码为脉冲模式。现有的训练算法要么通过反向传播只考虑有监督的SD，要么通过基于时序的可塑性考虑无监督的TD，这会导致性能瓶颈。因此，如何构建一个充分利用STD的学习框架是构成这项工作的主要动机的高性能SNN的根本要求。

　　然而，在(1)中获得LIF模型的解析解直接使得基于反向传播训练SNN变得不方便/模糊。这是因为整个网络将在SD和TD中呈现复杂的动态。为了解决这个问题，下面的事件驱动迭代更新规则：

可以很好地用于基于最后一个脉冲时刻t_i-1和突触前输入I(t)来近似估计(1)中的神经元电位u(t)。膜电位呈指数衰减，直到神经元接收到突触前输入，一旦神经元发出脉冲信号，就会开始新的更新回合。也就是说，神经元状态由I(t)的空间累积和u(t_i-1)的泄漏时间记忆共同决定。

　　正如我们所知，用于训练DNN的误差反向传播的效率极大地受益于梯度下降的迭代表示，它产生了SD反向传播中逐层误差传播的链式法则。这促使我们提出基于迭代LIF的SNN，其中迭代发生在SD和TD中，如下所示：

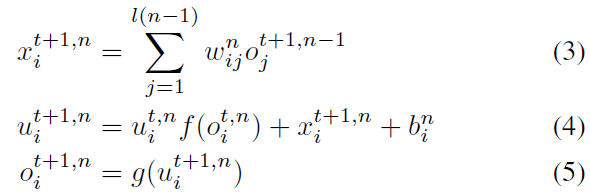
其中：

上式中，上标 t 表示时间 t 时刻，n和l(n)分别表示第n层和第n层神经元个数。w_ij为突触前层第 j 个神经元到突触后层第 i 个神经元的突触权重，o_j ∈ {0, 1}是第 j 个神经元的神经元输出，其中o_j = 1表示脉冲活动，o_j = 0表示没有发生。x_i是第 i 个神经元的突触前输入的简化表示，类似于原始LIF模型中的I。u_i是第 i 个神经元的神经元膜电位，b_i是与阈值V_th相关的偏差参数。
　　实际上，公式(4)-(5)也受到LSTM模型[25]-[27]的启发，通过使用遗忘门f(.)来控制TD记忆和使用输出门g(.)来发放脉冲。遗忘门f(.)控制TD中潜在记忆的泄漏程度，输出门g(.)在被激活时会产生脉冲活动。具体来说，对于一个小的正时间常数，f(.)可以近似为：

由于τe^-1/τ ≈ 0。这样，原始LIF模型可以转化为迭代版本，其中SD和TD中的递归关系都得到了清晰的描述，这对STD中的后续梯度下降训练很友好。

 

B. Spatio-Temporal Backpropagation Training

　　为了呈现STBP训练方法，我们定义了以下损失函数L，其中在给定时间窗口T下所有样本的均方误差要最小化：

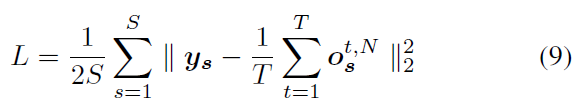
其中y_s和o_s分别表示第s个训练样本的标签向量和最后一层N的神经元输出向量。

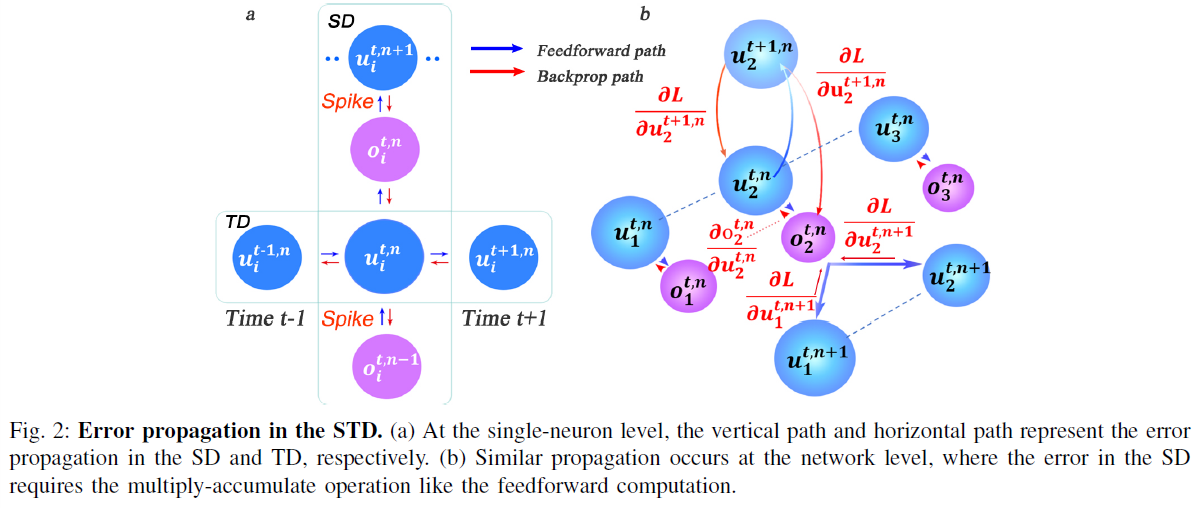
　　通过将等式(3)-(9)组合在一起，可以看出L是W和b的函数。因此，基于梯度下降的STBP算法需要获得L对W和b的导数。假设我们已经在时间 t 的每一层n处获得了和的导数，这是获得最终的和的必要步骤。图2描述了单神经元级别(图2.a)和网络级别(图2.b)的SD和TD中的误差传播(取决于推导)。在单神经元层面，传播被分解为SD的垂直路径和TD的水平路径。SD中误差传播的数据流类似于DNN的典型BP，即每个神经元累积来自上层的加权误差信号并迭代更新不同层的参数；而TD中的数据流共享相同的神经元状态，这使得直接获得解析解变得相当复杂。为了解决这个问题，我们使用所提出的迭代LIF模型在SD和TD方向上展开状态空间，从而可以区分不同时间步长的TD中的状态，从而实现迭代传播的链式规则。类似的想法可以在[28]中用于训练RNN的BPTT算法中找到。

　　现在，我们基于以下四种情况讨论如何获得完整的梯度下降。 首先，我们表示：

　　基于这四种情况，误差传播过程(取决于上述导数)如图2所示。在单神经元层面(图2.a)，传播分解为SD的垂直路径和TD的水平路径。在网络层面(图2.b)，SD中误差传播的数据流类似于DNN的典型BP，即每个神经元累积来自上层的加权误差信号并迭代更新不同层的参数；在TD中，神经元状态在时序方向上迭代展开，从而实现链式规则传播。最后，我们得到关于W和b的导数如下：

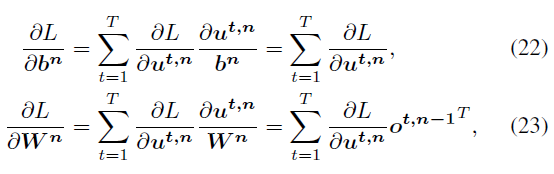
其中可以从等式(11)-(21)中获得。根据STBP给定W和b，我们可以使用梯度下降优化算法来有效训练SNN以实现高性能。

 

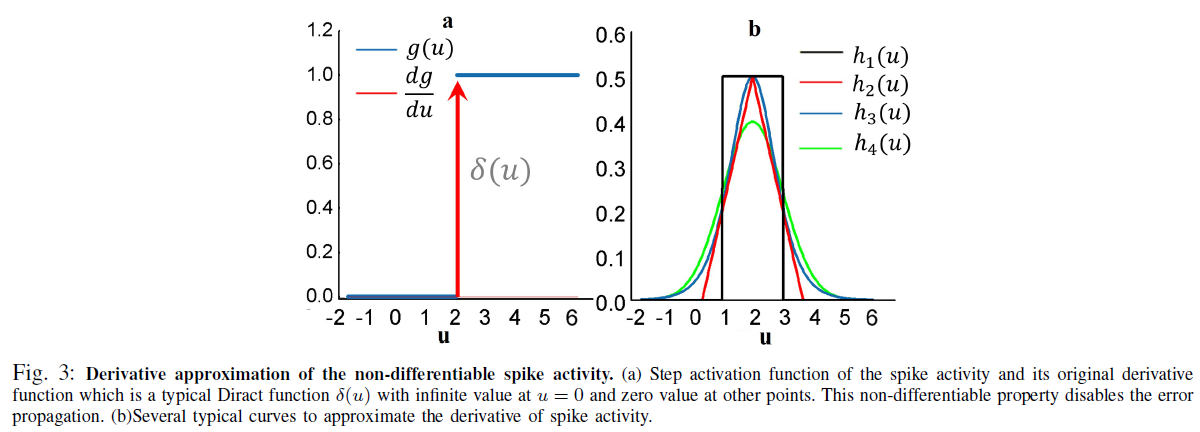
C. Derivative Approximation of the Non-differentiable Spike Activity

　　在前面的部分中，我们已经介绍了如何基于STBP获取梯度信息，但是每个脉冲时间点的不可微分问题还有待解决。实际上，公式(11)-(22)的STBP训练需要输出门g(u)的导数。理论上，g(u)是δ(u)的不可微狄拉克函数，这极大地挑战了SNN的有效学习[23]。g(u)除了在零处的无穷大值外，其他任何地方都具有零值，这会导致梯度消失或爆炸问题，从而禁用误差传播。现有方法之一将脉冲时间电位的不连续点视为噪声，并声称它有利于模型的鲁棒性[23][29]，但它没有直接解决脉冲活动的不可微性问题。为此，我们引入了四条曲线来近似图3.b中由h₁、h₂、h₃和h₄表示的脉冲活动的导数：

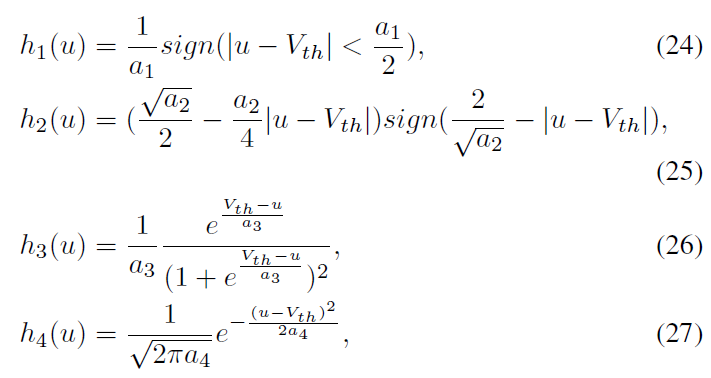
其中a_i(i = 1, 2, 3, 4)确定曲线形状和陡峭程度。实际上，h₁, h₂, h₃和h₄分别是矩形函数、多项式函数、sigmoid函数和高斯累积分布函数的导数。为了与狄拉克函数δ(u)一致，我们引入系数a_i来保证每个函数的积分为1。显然，可以证明上述所有候选都满足：

　　因此，STBP的公式(11)-(22)中的可以近似为：

在第III-C节中，我们将分析不同曲线和不同a_i值对SNN性能的影响。

 

III. RESULTS

A. Parameter Initialization

　　参数的初始化，如权重、阈值和其他参数，对于稳定整个网络的发放活动至关重要。我们应该同时确保突触前刺激的及时反应，但避免过多的脉冲降低神经元选择性。众所周知，预脉冲和权重的乘法累加操作和阈值比较是前向传播中计算的两个关键步骤。这表明权重和阈值之间的相对大小决定了参数初始化的有效性。在本文中，为了简化起见，我们将每个神经元中的阈值固定为常数，并且仅调整权重以控制活动平衡。首先，我们初始化从标准均匀分布中采样的所有权重参数：

然后，我们将这些参数归一化为：

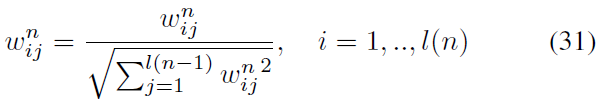
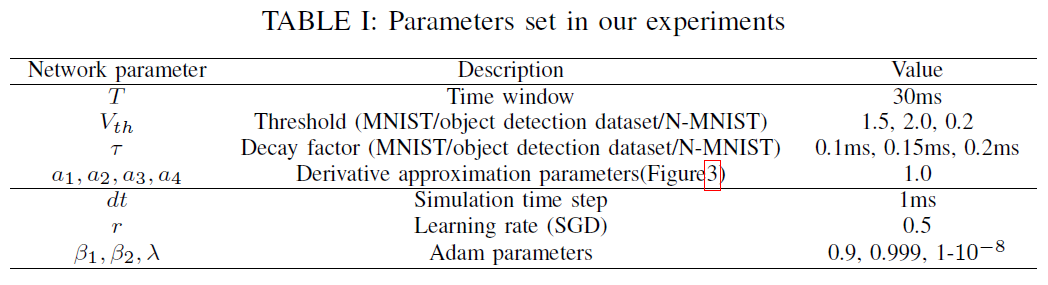
其他参数组列于表I中。此外，在我们工作中的所有模拟中，不再需要[19][23]中的任何复杂技能，例如固定数量比例重置、误差归一化、权重/阈值正则化等。

 

 

B. Dataset Experiments

　　我们在各种数据集上测试我们的SNN模型和STBP训练方法，包括静态MNIST和自定义对象检测数据集，以及动态N-MNIST数据集。第一层的输入应该是一个脉冲序列(spike train)，这需要我们将静态数据集中的样本转换成脉冲事件。为此，本文采用了从原始像素强度到发放率的Bernoulli采样。

　　1) Spatio-temporal fully connected neural network: Static Dataset. 手写数字的MNIST数据集[30](图4.b)和用于对象检测的自定义数据集[14](图4.a)被选中来测试我们的方法。MNIST由带有60000个标记的手写数字的训练集和由0-9的邮政编码生成的其他10000个标记数字的测试集组成。每个数字样本是一个28 × 28的灰度图像。目标检测数据集是我们实验室为行人检测创建的​​二类图像数据集。它包括1509个训练样本和631个测试样本的28 x 28灰度图像。通过检测是否有行人，一个图像样本被标记为0或1，如图4.a所示。图 4.c中上下两个子图分别是从对象检测数据集和MNIST上的样本示例的5 x 5像素的中心块转换而来的25个输入神经元的脉冲模式。图4.d举例说明了在STBP训练前后15ms内输出层的脉冲模式对数字9的刺激。开始时，输出层中的神经元随机发放，而训练后第10个神经元编码数字9最密集地发放，表明实现了正确的推理。

　　表II将我们的方法与其他几个在MNIST上使用类似MLP架构的高级结果进行了比较。尽管我们不使用任何复杂的技能，但所提出的STBP训练方法也优于所有报告的结果。我们可以达到98.89%的测试准确率，这是表现最好的。表III将我们的模型与对象检测数据集上的典型MLP进行了比较。对比模型是典型的人工神经网络(ANN)之一，即不是SNN，下面我们使用"非脉冲网络"来区分它们。可以看出，我们的模型比非脉冲MLP实现了更好的性能。请注意，来自对象检测数据集的输入脉冲序列的整体发放率高于来自MNIST数据集的输入脉冲序列，因此我们在模拟实验中将其阈值增加到2.0。

　　Dynamic Dataset. 与静态数据集相比，动态数据集，如N-MNIST[32]，包含更丰富的时间特征，因此更适合开发SNN的潜在能力。我们以N-MNIST数据库为例来评估我们的STBP方法在动态数据集上的能力。N-MNIST通过使用动态视觉传感器(DVS)[33]将上述静态MNIST数据集转换为其动态版本的脉冲序列。对于MNIST的每个原始样本，工作[32]控制DVS依次向等腰三角形的三个边方向移动(图5.b)，并收集每个像素的强度变化触发的生成脉冲序列。图5.a记录了数字0的跳视结果。每个子图记录了10ms内的脉冲序列，每100ms代表一个跳视周期。由于每个像素强度有两种可能的变化方向(更亮或更暗)，DVS可以捕获相应的两种脉冲事件，分别用开事件和关事件表示(图5.c)。由于N-MNIST允许在扫视过程中图像的相对位移，它产生34 x 34像素范围。从图5.c的时空表征中，我们可以看到开事件和关事件是如此不同，我们使用两个通道来区分它。因此，网络结构为34x34x2-400-400-10。

　　表IV将我们的STBP方法与N-MNIST数据集上的一些最新结果进行了比较。上面的5个结果基于ANN，下面的4个结果(包括我们的方法)使用SNN。人工神经网络方法通常采用基于帧的方法，在时间间隔(50ms ~ 300ms)内收集脉冲事件形成一帧图像，并使用传统的图像分类算法来训练网络。由于转换后的图像通常是模糊的，基于帧的预处理对模型性能有害，并放弃了硬件友好的事件驱动范式。从表IV可以看出，ANN的模型普遍比SNN的模型差。相比之下，SNN可以自然地处理事件流模式，并且通过更好地利用事件流的时空特征，与所有报告的ANN和SNN方法相比，我们提出的STBP方法实现了98.78%的最佳准确率。我们方法的最大优点是我们没有使用任何复杂的训练技巧，这有利于未来的硬件实现。

　　2) Spatio-temporal convolution neural network: 将我们的框架扩展到卷积神经网络结构可以让网络更深入，并赋予网络更强大的SD信息。这里我们使用我们的框架来建立时空卷积神经网络。与我们的时空全连接网络相比，主要区别在于输入图像的处理，我们使用卷积代替加权求和。具体来说，在卷积层中，每个卷积神经元接收卷积后的输入并根据LIF模型更新其状态。在池化层，由于SNN的二值编码不适合标准最大池化，我们使用平均池化代替。

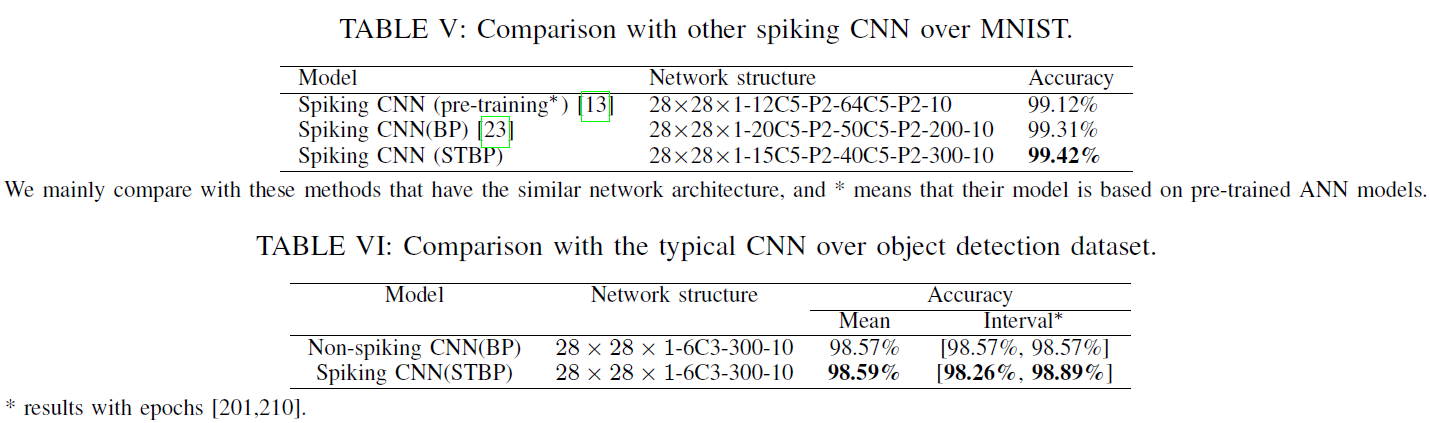
　　我们的脉冲CNN模型也在MNIST数据集和对象检测数据集上进行了测试。在MNIST中，我们的网络包含一个卷积层，核大小为5 x 5和两个平均池化层交替，然后是一个隐含层。和传统的CNN一样，我们使用弹性失真[36]来预处理数据集。表V记录了MNIST数据集上最先进的性能脉冲卷积神经网络。我们提出的脉冲CNN模型获得了98.42%的准确率，这优于其他报告的具有稍轻结构的脉冲网络。此外，我们在自定义对象检测数据库上配置相同的网络结构来评估所提出的模型性能。训练200个epoch后报告测试准确率。表VI表明我们的脉冲CNN模型可以实现与非脉冲CNN可比的性能。

 

C. Performance Analysis

　　1) The Impact of Derivative Approximation Curves: 在第II-B节中，我们引入了不同的曲线来近似脉冲活动的理想导数。本文试图分析不同近似曲线对测试精度的影响。在MNIST数据集上进行了实验，网络结构为784-400-10。在训练200个epoch后报告测试精度。首先，我们比较了不同曲线形状对模型性能的影响。在我们的模拟中，我们使用图3.b中所示的h1、h2、h3和h4。图6.a说明了不同形状近似的结果。我们观察到，不同的非线性曲线，如h1、h2、h3和h4，对性能的影响很小。

　　此外，我们以矩形近似为例，探讨了宽度对实验结果的影响。我们设定a1=0.1, 1.0, 2.5, 5.0, 7.5, 10和相应的结果绘制在图6.b中。不同的颜色表示不同的a₁值。a₁值过大或过小都会导致性能下降，在我们的模拟中，a₁=2.5达到了最高的测试精度，这意味着矩形的宽度和陡度会影响模型性能。结合图6.a和图6.b，它表明，近似脉冲活动推导的关键点是捕捉非线性性质，而具体形状并不那么关键。

　　2) The Impact of Temporal Domain: 这项工作的一个主要贡献是将时域引入现有的基于空域的BP训练方法中，充分利用了SNN的时空动态特性，实现了高性能的训练。现在我们定量分析TD项目的影响。实验配置与前一节(784-400-10)我们还报告了经过200个epoch训练后的测试结果。此处，SD中的现有BP称为SDBP。

　　表VII记录了模拟结果。SDBP的测试精度低于STBP在不同数据集上的测试精度，这表明时间信息有利于模型性能的提高。具体而言，与STBP相比，SDBP在目标跟踪数据集上的准确度损失为1.21%，比MNIST上的损失大5倍。结果还表明，SDBP的性能不够稳定。除了数据集本身的干扰外，这种变化的原因可能是SNN训练的不稳定性。实际上，SNN的训练在很大程度上依赖于参数的初始化，这对于SNN应用来说也是一个巨大的挑战。在许多已有的研究工作中，研究人员通常利用一些特殊的技能或机制来提高训练性能，如横向抑制、正则化、归一化等。相比之下，使用我们的STBP训练方法，可以在相同的网络上获得更高的性能。具体来说，在MNIST和目标检测数据集上，STBP的测试准确率分别达到98.48%和98.32%。请注意，STBP可以在不使用任何复杂训练技能的情况下实现高精度。这种稳定性和鲁棒性表明，TD中的动态基本上包含了SNN计算的巨大潜力，这项工作确实提供了一种新思路。

 

IV. CONCLUSION

　　在这项工作中，通过利用网络中的时空信息，建立了一个统一的框架，允许监督训练脉冲神经网络，就像在深度神经网络(DNN)中实现反向传播一样。我们的主要贡献总结如下：

• 我们提出了一个基于迭代LIF模型的框架，使我们能够在SNN上实现时空反向传播。与以往主要关注其空间域特征的方法不同，我们的框架进一步结合和利用了SNN在空间域和时间域的特征；

• 我们设计了STBP训练算法，并在MLP和CNN架构上实现了它。STBP已在静态和动态数据集上得到验证。结果表明，我们的模型在具有脉冲MLP和CNN的相对小规模网络上优于最先进的SNN，在动态NMNIST数据集上优于具有相同网络大小的DNN。我们的算法的一个吸引人的优点是，它不需要现有方案通常需要的额外训练技术，并且更容易在大规模网络中实现。结果还表明，利用时空复杂性解决问题可以更好地发挥SNN的潜力；

• 我们引入了一个近似导数来解决脉冲活动的不可微问题。控制实验表明，逼近曲线的陡峭度和宽度会影响模型的性能，而逼近的关键是捕捉非线性性质，而具体形状并不那么关键。

　　因为大脑结合了时空域的复杂性来处理输入信息，我们还想说，在SNN上实现STBP比在DNN上应用BP更具生物可行性。STBP不依赖于太多的训练技巧，这使得它对硬件更加友好，对于具有在线学习能力的神经形态芯片的设计非常有用。关于未来的研究课题，我们认为有两个问题是非常必要和重要的。一个是应用我们的框架来解决更多的时序特性问题，如动态数据处理、视频流识别和语音识别。二是如何加速基于GPU/CPU或神经形态芯片的大规模SNN的监督训练。前者旨在进一步利用SNN丰富的时空特性来处理动态问题，后者可能极大地促进大规模SNN在现实生活场景中的应用。