Surrogate Gradient Learning in Spiking Neural Networks
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

arXiv: Neural and Evolutionary Computing, (2019)
Abstract
脉冲神经网络是自然界用于容错和节能信号处理的通用解决方案。为了将这些优势转化为硬件,越来越多的神经形态脉冲神经网络处理器试图模拟生物神经网络。这些发展产生了对方法和工具的迫切需求,以使此类系统能够解决现实世界的信号处理问题。与传统的神经网络一样,脉冲神经网络可以在真实的、特定领域的数据上进行训练。然而,他们的训练需要克服与他们的二元性和动态性相关的许多挑战。本文逐步阐明了训练脉冲神经网络时通常遇到的问题,并引导读者了解脉冲环境中突触可塑性和数据驱动学习的关键概念。为此,它概述了现有方法,并介绍了替代梯度方法,特别是作为克服上述挑战的一种特别灵活且有效的方法。
I. INTRODUCTION
生物脉冲神经网络(SNN)是进化对信号处理问题的高效解决方案。因此,从大脑中汲取灵感是设计更高效计算架构的自然方法。在机器学习领域,循环神经网络(RNN)是一类内部状态随时间变化的有状态神经网络(Box. 1),已被证明在解决实时模式识别和带噪时间序列预测问题方面非常有效[1]。RNN和生物神经网络共享几个属性,例如类似的通用架构、时间动态和通过权重调整学习。基于这些相似性,越来越多的工作现在正在RNN和广泛用于计算神经科学的LIF神经元网络之间建立形式上的等价关系[2-5]。
RNN通常使用优化程序进行训练,在该程序中调整参数或权重以最小化给定的目标函数。由于各种外在因素(例如数据的噪声和非平稳性),以及优化具有长期时间和空间依赖性的函数的固有困难,有效地训练大规模RNN具有挑战性。在SNN和二元RNN中,这些困难由于其输出的二元性质所隐含的不可微动态而更加复杂。虽然大量工作已经成功地证明了训练没有隐含单元的两层SNN[6-8]和具有循环突触连接的网络[9, 10],但训练具有隐含层的更深SNN的能力仍然是一个主要障碍。由于隐含单元和深度对于有效解决许多现实世界问题至关重要,因此克服这一障碍至关重要。
随着网络模型变得越来越大并进入嵌入式和汽车应用,它们的电源效率变得越来越重要。现在正在设计可以在专用硬件上本地高效运行的简化神经网络架构。例如,这包括模拟SNN动态的二元神经元网络或神经形态硬件[11]。这两种类型的网络都省去了耗能巨大的浮点乘法,与在传统硬件上执行的神经网络相比,它们特别有利于低功耗应用。
这些新的硬件开发迫切需要能够在SNN和二元RNN中进行高效推理和学习的工具和策略。在本文中,我们讨论并解决训练具有隐含层的SNN的固有困难,并介绍用于成功实现它们的各种策略和近似值。

II. UNDERSTANDING SNNS AS RNNS
我们首先将SNN正式映射到RNN。将SNN制定为RNN将允许我们直接迁移和应用RNN的现有训练方法,并将作为本文其余部分的概念框架。
在我们继续之前,先介绍一下术语。我们在最广泛的意义上使用术语RNN来指代其状态根据一组循环动态方程随时间演变的网络。这种动态复发可能是由于网络中神经元之间明确存在反复突触连接。这是对什么是RNN的普遍理解。但重要的是,在没有循环连接的情况下也会出现动态循环。例如,当使用具有内部动态的有状态神经元或突触模型时,就会发生这种情况。由于网络在特定时间步骤的状态反复取决于其在前一时间步骤的状态,因此这些动态本质上是循环的。在本文中,我们使用术语RNN来表示表现出一种或两种类型的循环的网络。此外,我们为具有显式循环突触连接的网络子集引入了术语循环连接神经网络(RCNN)。我们现在将证明两者都承认相同的数学处理,尽管它们的动态特性可能大不相同。
为此,我们将首先介绍在计算神经科学中广泛使用的具有基于电流的突触的LIF神经元模型[12]。接下来,我们将在离散时间重新构建这个模型,并展示它与具有二元激活函数的RNN的形式等效。熟悉LIF神经元模型的读者可以跳过以下步骤直至公式(5)。
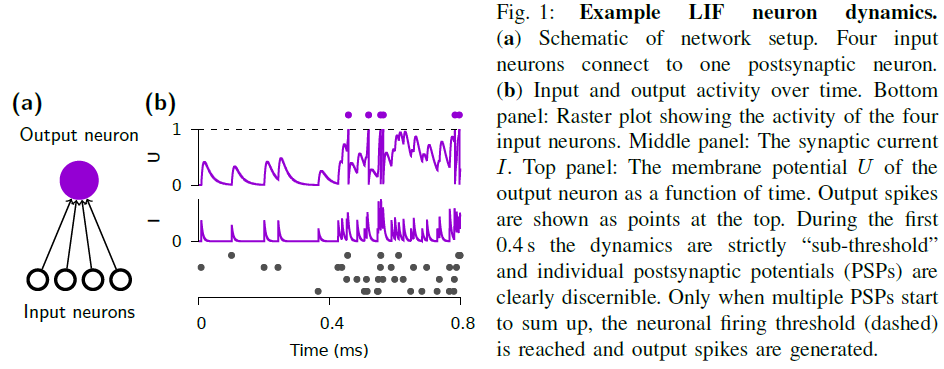



我们现在已经看到SNN构成了RNN的一个特例。但是,到目前为止我们还没有解释它们的参数是如何设置来实现特定的计算功能的。这是本文其余部分的重点,我们在其中介绍了各种学习算法,这些算法系统地更改参数以实现特定功能。
III. METHODS FOR TRAINING RNNS
强大的机器学习方法能够为从时间序列预测到语言翻译,再到自动语音识别的各种任务训练神经网络[1]。在下面,我们先讨论最常用的方法,然后再分析它们对SNN的适用性。
有几个陈规定型的成分定义了训练过程。第一个要素是成本或损失函数,当网络的响应与期望行为相对应时,该函数被最小化。例如,在时间序列预测中,该损失可以是预测值和真实值之间的平方差。第二个因素是一个机制,更新网络的权重,以尽量减少损失。实现这一点的最简单和最强大的机制之一是对损失函数执行梯度下降。在具有隐含单元(即其活动通过其他单元间接影响损失的单元)的网络架构中,参数更新包含与其投射到的下游单元的活动和权重相关的项。梯度下降学习通过导数链规则为这些更新提供显式表达式来解决信度分配问题。正如我们现在将看到的,隐含单元参数的学习依赖于计算这些梯度的有效方法。在讨论这些方法时,我们区分了对多层感知器(MLP)和RNN有相同影响的空间信度分配问题和只发生在RNN中的时序信度分配问题。我们现在讨论提供这两种类型的信度分配的常见算法。

A. Spatial credit assignment
为了训练MLP,需要跨层及其各自的单元在空间上分配信度或责任。这种空间信度分配问题最常通过误差算法的反向传播(BP)来解决(Box. 2)。以其最简单的形式,该算法将误差从网络输出"反向"传播到上游神经元。使用BP调整隐含层权重确保权重更新将降低当前训练示例的成本函数,前提是学习率足够小。虽然这种理论上的保证是可取的,但它是以某些通信要求为代价的——即梯度必须通过网络传回——以及增加的内存要求,因为神经元状态需要保留在内存中,直到误差可用。
B. Temporal credit assignment
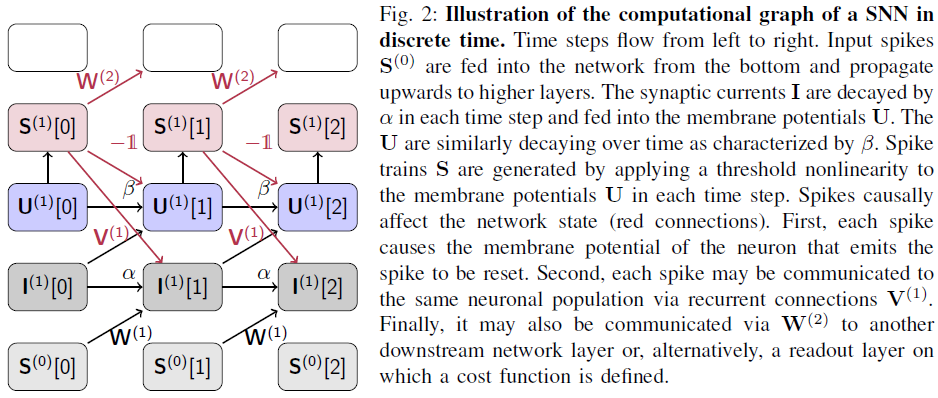
在训练RNN时,我们还必须考虑网络活动的时间互依赖性。这需要解决时序信度分配问题(图2)。有两种常见的方法可以实现这一点:
1)"反向"方法:该方法通过及时"展开"网络(Box. 2)应用与空间信度分配相同的策略。时序反向传播(BPTT)通过展开网络反向传播误差来解决时序信度分配问题。此方法在完成前向传播后按时间向后工作。在展开的网络上使用标准BP可以直接使用现代机器学习工具包中提供的自动微分工具[3, 13]。
2)前向方法:在某些情况下,及时传播梯度计算所需的所有信息是有益的[14]。该公式是通过计算成本函数L[n]的梯度并保持RNN的循环结构来实现的。例如,前馈权重W的"前向梯度"变为:


总之,存在训练RNN的有效算法。我们现在将专注于训练SNN。
IV. CREDIT ASSIGNMENT WITH SPIKING NEURONS: CHALLENGES AND SOLUTIONS
A. Smoothed spiking neural networks
B. Surrogate gradients
V. APPLICATIONS
A. Feedback alignment and random error backpropagation
B. Supervised learning with local three factor learning rules
C. Learning using local errors
D. Learning using gradients of spike times
VI. CONCLUSION



