Gradient-Free Neural Network Training via Synaptic-Level Reinforcement Learning
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Preprint. Under review.
Abstract
神经信息处理中的一个持续挑战是:神经元如何调整它们的连接性以随着时间的推移提高任务性能(即实现学习)?人们普遍认为,在特定的大脑区域,如基底节,有一个一致突触级的学习机制来实现学习。然而,这一机制的确切性质仍不清楚。在此,我们在训练连接模型中调查使用通用突触级的算法。具体来说,我们提出了一个基于强化学习(RL)的算法来生成和应用一个简单的生物启发的多层感知器(MLP)模型的突触级学习策略。在该算法中,每个MLP突触的动作空间由对突触权重的微小增加、减少或零动作组成,每个突触的状态由最后两个动作和全局奖励信号组成。二值奖励信号表示前两次迭代之间模型损失的增加或减少。该算法产生了一个静态的突触学习策略,当应用于模拟的决策边界匹配和光学字符识别任务时,它可以同时训练20000多个参数(即突触)和一致的MLP收敛。静态策略是鲁棒的,因为它相对于自适应策略产生更快和更一致的训练,并且与激活函数、网络形状和任务无关。训练的网络产生的字符识别性能可与梯度下降训练的同形网络相媲美。0隐单元字符识别试验的平均验证准确率为88.28%,比用梯度下降法训练的同一MLP高1.86±0.47%。32个隐单元字符识别测试的平均验证准确率为88.45%,比用梯度下降法训练的同一MLP低1.11±0.79%。与传统的基于梯度下降的优化方法相比,该方法有两个显著的优点。首先,我们的新方法的鲁棒性和对梯度计算的不依赖性为训练难以微分的人工神经网络(如SNN和RNN)的新技术打开了大门。其次,该方法的简单性为进一步开发类似于元胞自动机的局部规则驱动的机器智能多智能体连接模型提供了独特的机会。
1 Introduction
了解生物神经元调整其连接性以实现学习的方法对神经科学和机器学习(ML)等具有重大影响[1, 31]。对于ML,它将支持高度并行化和鲁棒的连接模型,这些模型不依赖于传统的梯度下降和反向传播方法。在神经科学中,它将提高对有效神经计算的基本要求的理解[28]。然而,当通过生物神经元行为的分析和建模以及通过生成更抽象的连接系统[21, 30, 5, 20]的计算模型进行调查时,这个问题已被证明具有挑战性。在此,我们简要介绍了迄今为止在这个问题上的生物学和计算动机研究方向的努力。
该研究领域中以生物学为动机的神经科学研究经常关注皮层、基底神经节和丘脑之间的通路(称为CBGT通路)[12, 22]。据了解,这个大脑区域与决策任务中的动作选择密切相关,并且连接性会随着时间的推移而调整,以最大化多巴胺能奖励信号[7]。关于这一现象背后机制的主要悬而未决的问题是:如何将"信度"分配给任何一个神经元或突触,以便为连接性的后续调整提供信息[26]?由于奖励信号、动作选择和通路连接变化在空间和时间上彼此相距甚远,研究人员一直在努力寻找有效且有凝聚力的解决方案来解决这个信度分配问题。由于难以模拟具有生物现实意义的神经元模型[10]的大型网络,研究变得更加复杂。随着时间的推移,该领域的研究已广泛收敛于以下假设:在这些大脑区域中采用了一些一致的突触级RL算法来实现学习[26]。
该领域对抽象连接模型的计算驱动研究应用RL或相关技术来训练神经网络模型[21, 5, 30, 20]。在这些研究中,神经元通常被设计为部分可观察马尔可夫决策过程(POMDP)中的RL智能体,其奖励信号基于任务的网络性能。这些工作在智能体状态空间的制定方面有所不同,有些工作引入了竞争奖励模式[21]来激励生物现实主义。然而,在本领域中观察到的关键问题要么是将学习任务挑战的"权重"放在现有的非生物学可行技术上,和/或错误地制定了每个神经元的动作空间。例如,[21] 将每个神经元建模为使用梯度下降(策略梯度)方法优化的深度Q学习神经网络。然后在OpenAI的Cartpole上评估网络,这是使用策略梯度方法训练的深度Q学习神经网络的标准任务[2, 29]。两者[21, 5]还将每个神经元的动作空间定义为"发放"或"不发放",而不是作为一组改变突触连接的动作,这种方法不受神经科学和现代机器学习文献的支持。[21, 5, 30, 20]都为每个神经元/权重训练单独的策略,而不是训练所有突触应用的相同策略,如上面讨论的神经科学文献所建议的那样。总的来说,这些工作在网络训练中取得了一定的成功。
我们提出了以下高级设计更改:
- 将基本的RL智能体构建为突触而不是神经元。
- 在所有突触上训练和应用相同的突触强化学习策略。
- 将每个突触的动作空间设置为由对突触权重的小增量、小减量和空动作组成。
- 将突触状态表示为最后n个突触动作和奖励。
- 在每个时间步骤使用通用二值奖励,表示MLP训练损失在最近两次迭代之间是增加还是减少。
这种公式使问题在计算和统计上可行,特别是对于大型网络。为所有突触训练和应用相同的突触策略提供了更多的数据来通知单个策略,这会导致更高的收敛机会和给定策略形式的过拟合的机会更低[27, 29]。选择突触作为基本的强化学习智能体也简化了动作空间,因为生物神经元可以有数千个突触[14],而根据隐含层大小,在光学字符识别等标准任务上训练的MLP可以具有任意数量的突触(每个神经元)。一种更新神经元连接性的简单方法将为每个神经元生成一个动作空间,其维度与层大小相同。
虽然神经科学文献提出了更大且可能更复杂的突触状态空间和奖励信号,其中包括神经元/突触活动等其他因素[26, 4],但我们发现,这种简单的公式可以实现令人惊讶的有效MLP训练,尤其是在静态(学到的)应用突触学习策略。这种静态策略可以同时训练超过20000个参数,并始终收敛于notMNIST 数据集[3]上的随机决策边界匹配和光学字符识别任务。学到的网络还产生与使用梯度下降训练的相同形状的网络相当的字符识别性能。使用所提出的突触RL方法和梯度下降对0和32个隐含单元OCR MLP进行了5次训练。0隐含单元突触RL MLP产生了88.28±0.41%的平均最终验证精度,而0隐含单元梯度下降训练的MLP产生了86.42±0.22%的最终验证精度。32个隐含单元突触RL测试的平均验证精度为88.45±0.6%,而32个隐含单元梯度下降测试的平均验证精度为89.56±0.52%。
2 Approach
我们试图了解强化学习方法在多大程度上可以应用于生成用于训练MLP的突触级策略。尽管与生物神经元网络的复杂性相比,MLP显得苍白无力,但它们提供了一个易于模拟的抽象连接主义模型,该模型与生物神经元具有一些高级属性[25]。所提出的突触级学习算法的形式是由关于生物神经元的几个假设所决定的。由于生物神经元是计算能力有限的单个细胞[19],我们假设生物神经网络中的每个突触都应用相对简单的策略来随时间调整其连接性。该策略考虑了包括全局奖励信号(例如,多巴胺能信号)和突触自身过去的连接变化在内的信息,以告知随后的连接变化。我们怀疑每个突触应用的策略在给定的大脑区域中大致相同,行为和连通性的差异源于局部信息的差异,而不是完全不同的策略的应用。随着时间的推移,该策略会导致某些奖励信号的最大化。
鉴于这些假设,我们将问题构建为POMDP,突触作为基本的强化学习(RL)智能体。在这项工作中,我们应用TD学习更新方程来学习Q函数以训练MLP神经网络的突触。我们测试了该方法在模拟数据和光学字符识别任务上的适用性和通用性。
2.1 MLP notation
以下符号用于MLP[13, 27]:

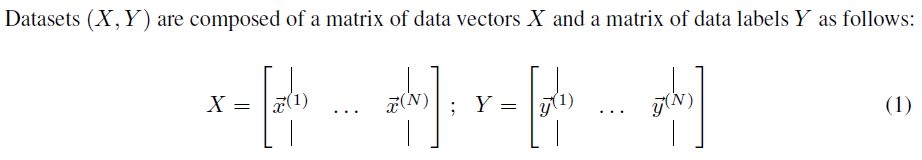
2.2 Synaptic reinforcement learning
用于推断MLP参数![]() 的基于梯度的方法需要在整个网络中反向传播误差信号,并且在生物神经网络中不容易观察到[31]。我们将这个问题定义为POMDP中的多智能体RL问题,如下所示:每个突触都被视为执行相同策略的RL智能体。该策略将突触状态映射到动作(即改变突触权重)。应用时序差分更新公式来推导Q函数,使得总奖励随着时间的推移而最大化[27, 29]。
的基于梯度的方法需要在整个网络中反向传播误差信号,并且在生物神经网络中不容易观察到[31]。我们将这个问题定义为POMDP中的多智能体RL问题,如下所示:每个突触都被视为执行相同策略的RL智能体。该策略将突触状态映射到动作(即改变突触权重)。应用时序差分更新公式来推导Q函数,使得总奖励随着时间的推移而最大化[27, 29]。
在离散时间步骤,我们为所提出的突触RL模型定义以下内容:

2.3 Training
在这项研究中,Q值学习通常是一个双重过程,其中神经网络参数![]() 与Q函数和策略π同时训练。策略π生成后,也可以静态应用。在策略训练期间,使用以下Q学习[29]的TD学习更新公式更新Q值:
与Q函数和策略π同时训练。策略π生成后,也可以静态应用。在策略训练期间,使用以下Q学习[29]的TD学习更新公式更新Q值:
![]()
其中αq > 0是Q学习率。训练伪代码如下:

3 Experiments & results
4 Discussion
5 Broader impact


