Backpropamine: training self-modifying neural networks with differentiable neuromodulated plasticity
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Published as a conference paper at ICLR 2019
Abstract
动物大脑令人印象深刻的终生学习主要是通过突触连通性的可塑性变化实现的。重要的是,这些变化不是被动的,而是由神经调节主动控制的,而神经调节本身就是在大脑的控制之下。所产生的大脑自我调节能力在学习和适应中起着重要作用,并且是生物学RL的主要基础。在此,我们首次展示了具有这种神经调节可塑性的ANN可以通过梯度下降进行训练。在扩展关于可微赫布可塑性的先前工作的基础上,我们提出了神经调节可塑性的可微分公式。我们表明,神经调节可塑性改进了RL和监督学习任务上神经网络的性能。在一项任务中,基准语言建模任务上(控制参数数量)具有数百万个参数的神经调节可塑性LSTM优于标准LSTM。我们得出结论,可塑性的可微神经调节为训练神经网络提供了一个强大的新框架。
1 INTRODUCTION
处理时间扩展任务的神经网络必须能够存储过去事件的迹。通常,过去事件的记忆是通过循环连接回荡的神经活动来维持的;存在其他处理时间信息的方法,包括记忆网络(Sukhbaatar et al., 2015)或时序卷积(Mishra et al., 2017)。然而,从本质上讲,大脑中长期学习和记忆的主要基础是突触可塑性-突触权重作为持续活动的函数而自动改变(Martin et al., 2000; Liu et al., 2012)。可塑性使大脑能够长期存储有关其环境的信息,这对于进化以直接烙印到固有连接中是不可能的或不切实际的(例如一生中不同的事物,比如人们说的语言)。
重要的是,这些修改不是被动过程,而是由专用系统和机制在瞬间进行主动调节:大脑可以根据其输入和计算"决定"何时何地修改自己的连通性。这种可塑性的神经调节涉及多种化学物质(特别是多巴胺; Calabresi et al., 2007; He et al., 2015; Li et al., 2003; Yagishita et al., 2014),在学习和适应中起着重要作用(Molina-Luna et al., 2009; Smith-Roe&Kelley, 2000; Kreitzer&Malenka, 2008)。通过允许大脑根据进行中的状态和事件来控制自己的修改,可塑性的神经调节可以过滤掉无关的事件,同时选择性地吸收重要信息,消除先前所学知识的灾难性遗忘,并通过以奖励依赖的方式改变其自身的连通性来实现独立的RL算法(Schultz et al., 1997; Niv, 2009; Frank et al., 2004; Hoerzer et al., 2014; Miconi, 2017; Ellefsen et al., 2015; Velez&Clune, 2017)。
神经调节可塑性的复杂组织并不是偶然的:它是由长期的进化优化过程产生的。进化不仅设计了大脑的一般连接方式,而且还塑造了控制神经调节的机制,赋予大脑精心调整的自我调节能力,并实现了有效的终生学习。实际上,这种进化与可塑性的耦合是一个元学习过程(元学习的最原始的,也是迄今为止最强大的示例),由此,一个简单但功能强大的优化过程(自然选择的进化)就发现了如何安排基本的构建模块以产生非常有效的学习智能体。
从自然界中汲取灵感,几位作者表明,进化算法可以设计具有神经调节可塑性的小型神经网络(大约数百个连接)(请参见下面的"相关工作"部分)。但是,机器学习中许多令人瞩目的最新进展都是使用基于梯度的方法(可以将误差信号直接转换为权重梯度)而不是进化(必须通过随机权重空间探索来发现梯度)。如果我们可以使神经调节可塑性网络适应梯度下降,那么我们可以利用基于梯度的方法来优化和研究神经调节可塑性网络,从而扩展当前深度学习结构的能力,以包括这些重要的生物学启发的自我修改能力。
在此,我们基于可微的可塑性框架(Miconi, 2017; Miconi et al., 2018)来实现可微的神经调节可塑性。作为结果,据我们所知,我们首次能够训练具有梯度下降的神经调节可塑性网络。我们称其框架为backpropamine,是指其在通过反向传播训练的ANN中模拟天然神经调节剂(如多巴胺)作用的能力。我们的实验结果表明,在简单的RL任务和涉及数百万个参数网络的复杂语言建模任务上,神经调节可塑性网络的性能均优于不可塑和不可调节的可塑性网络。通过证明可以通过梯度下降来优化神经调节的可塑性,backpropamine框架潜在地提供了更强大的神经网络类型,包括循环和前馈,可用于所有对神经网络产生巨大影响的领域。
2 RELATED WORK
长期以来,人们一直在进化计算中研究过神经调节可塑性。在各种任务中,具有神经调节可塑性的进化网络表现优于非神经调节和不可塑性网络(例如Soltoggio et al., 2008; Risi&Stanley, 2012; 有关综述,请参见Soltoggio et al., 2017)。进化网络中神经调节的主要重点是减轻灾难性遗忘,也就是说,允许神经网络学习新技能而不会覆盖以前学习的技能。通过仅在与当前正在执行的任务相关的神经权重的子集中激活可塑性,其他权重中存储的有关不同任务的知识就保持不变,从而减轻灾难性遗忘(Ellefsen et al., 2015; Velez&Clune, 2017)。但是,从历史上看,进化网络相对较小,并且在低维问题空间上运行。
可微的可塑性框架(Miconi, 2016; Miconi et al., 2018)允许通过梯度下降来优化单个突触连接的可塑性,与标准突触权重相同。然而,虽然它可以在某些任务上提高循环性能而不产生可塑性,但这种方法仅促进了被动且非调节性的可塑性,其中权重变化根据突触前/后的活动而自动发生。在此,我们扩展此框架以实现可微的神经调节可塑性,其中连接可塑性可以通过网络计算的信号在瞬间进行调节。此扩展使网络本身可以决定其生命周期中何时何地可塑,从而赋予网络真正的自我修改能力。
还有其他可以想象的但更复杂的方法来训练自我修改网络。例如,权重修改本身可以通过神经网络进行计算(Schmidhuber, 1993b; Schlag&Schmidhuber, 2017; Munkhdalai&Yu, 2017; Wu et al., 2018)。但是,到目前为止,还没有一种简单的方法可以通过梯度下降而不是进化来直接优化单个网络中可塑性的神经调节本身,如本文所研究的那样。
3 METHODS
3.1 BACKGROUND: DIFFERENTIABLE HEBBIAN PLASTICITY
目前的工作是建立在现有的可塑性框架(Miconi, 2016; Miconi et al., 2018)的基础上的,该框架允许梯度下降不仅优化权重,而且优化每个连接的可塑性。在此框架中,网络中的每个连接都增加了一个赫布可塑性元件,该可塑性元件会由于正在进行的活动而自动增长和衰减。实际上,每个连接都包含一个固定和一个可塑性元件:
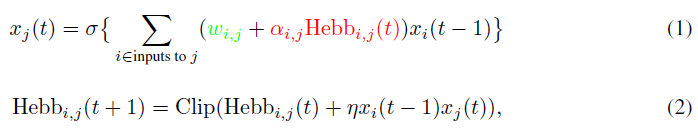
其中xi(t)是时间 t 处神经元 i 的输出,σ是非线性(在所有实验中我们都使用tanh),wi,j是神经元 i 和 j 之间连接的基准(不可塑)权重,并且αi,j是可塑性系数(可缩放连接可塑性元件的大小)。可塑性成分用赫布迹Hebbi,j表示,其在连接i, j处累积突触前和突触后活动的乘积,如等式2所示。
Hebbi,j在每个回合/一生的开始时初始化为零,并根据等式2自动更新:这是纯粹的回合/一生中的量。相比之下,wi,j,αi,j和η是网络的结构分量,通过回合/生命周期之间的梯度下降进行了优化,以最小化回合中的期望损失。
等式2中的函数Clip(x)是将Hebbi,j约束为范围[-1, 1],以消除赫布学习固有的不稳定性。在以前的工作中(Miconi et al., 2018),该函数要么是简单的衰减项,要么是实现Oja规则的正则化(Oja, 2008)。在本文中,它只是一个硬裁剪(如果x > 1,则x ← 1;如果x < -1,则x ← -1)。与以前使用的操作相比,这种简单的操作在本文的任务上产生了相同或更高的性能。
请注意参数η和αi,j之间的区别:η是可塑性连接的生命内"学习率",它确定将新信息整合到可塑性元件中的速度,而αi,j是比例参数,它确定可塑性元件的最大量级(因为Hebbi,j被限制在范围[-1, 1]内)。
重要的是,与其他使用均匀可塑性的方法(Schmidhuber, 1993a)相比,包括"快速权重"(Ba et al., 2016),每个连接中的可塑性量(以αi,j表示)是可训练的,从而允许元优化器来设计复杂的学习策略(有关这一点的讨论,请参见Miconi et al., 2018;实验性比较表明并解释了可微可塑性比均匀可塑性网络优越的性能)。
可微可塑性的一个重要方面是易于实现:与标准的循环网络实现相比,实现可塑性循环网络仅需要少于四行额外的代码行(Miconi et al., 2018)。下面描述的Backpropamine框架继承了这种简单性。特别是,"简单的神经调节"方法不需要针对可塑性的任何额外代码,而仅是对其的修改。
3.2 BACKPROPAMINE: DIFFERENTIABLE NEUROMODULATION OF PLASTICITY
两种方法被提出以在可塑性区域内引入神经调节可塑性。在这两种情况下,可塑性都是通过网络控制的神经调节信号M(t)在瞬间之间进行调节的。M(t)的计算可以通过多种方式进行;目前,它只是网络的单个标量输出,可以直接使用(用于简单的RL任务),也可以通过元学习到的权重向量使用(每个连接一个,对于语言建模任务)。现在,我们解释如何将可塑性的等式修改为利用该神经调节信号。
3.2.1 SIMPLE NEUROMODULATION
在此框架中引入神经调节可塑性的最简单方法是使(全局)参数η取决于网络中一个或多个神经元的输出。由于η实质上决定了可塑性变化的速率,因此将其置于网络控制之下,可使网络确定在任何给定时间应如何进行可塑性连接。因此,在这个简单的神经调节变量中,对以上等式的唯一修改是用等式2的η代替与网络计算的时变神经调节信号M(t)。即,等式2被替换为:

3.2.2 RETROACTIVE NEUROMODULATION AND ELIGIBILITY TRACES
更复杂的方案是可能的。特别是,我们介绍了另一种神经调节方案,该方案从神经调节多巴胺对动物大脑中赫布可塑性的短期追溯作用中获得启发。在一些实验中,多巴胺被证明可在约1s的短时间内追溯过去活动所诱导的可塑性(Yagishita et al., 2014; He et al., 2015; Fisher et al., 2017; Cassenaer&Laurent, 2012)。因此,赫布可塑性不会直接改变突触权重,而是会产生快速衰减的"潜在"权重变化,只有当突触在短时间内接收到多巴胺时,这种变化才被纳入实际权重。作为结果,生物学的赫布迹实质上实现了所谓的资格迹(Sutton et al., 1998),保留了哪个突触对最近的活动有贡献的记忆,而多巴胺信号调节了这些资格迹向实际可塑性变化的转化。这样的机制已经在计算神经科学研究中被建模,例如(Izhikevich, 2007; Hoerzer et al., 2014; Fiete et al., 2007; Soltoggio&Steil, 2013; Miconi, 2017)(有关此概念的最新评论,请参见Gerstner et al., 2018)。
我们的框架可以轻松适应这种多巴胺对可塑性影响的更为精确的模型。我们只需用两个等式替换前面的等式2:
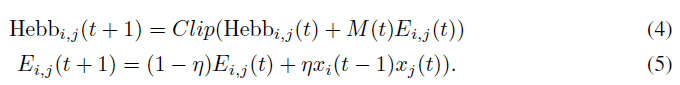
这里Ei,j(t)(连接i, j处的资格迹)是突触前后活动的赫布乘积的简单指数均值,并且具有可训练的衰减因子η。连接的实际可塑性元件Hebbi,j(t)(请参见等式1)仅累加此迹,但受到多巴胺信号M(t)当前值控制。注意,M(t)可以是正值或负值,近似于基准多巴胺水平上升和下降的影响(Schultz et al., 1997)。
4 EXPERIMENTS
4.1 TASK 1: CUE-REWARD ASSOCIATION
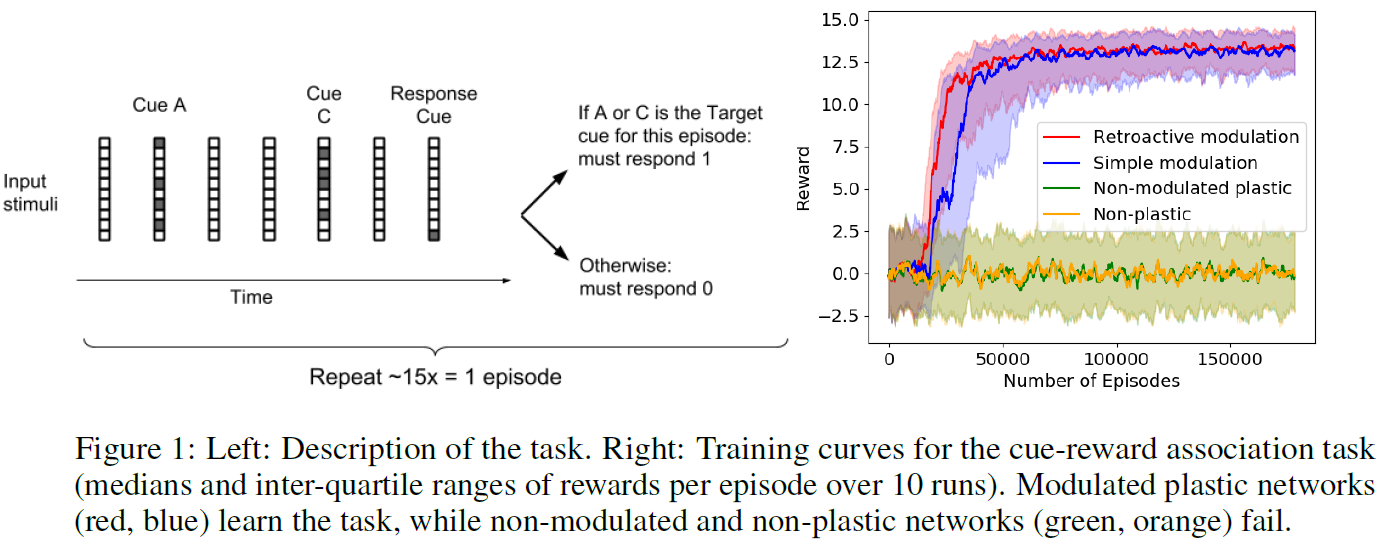
我们的第一个测试任务是一个简单的元学习问题,它模仿动物行为学习任务,如图1(左)所示。在每个回合中,任意选择四个输入提示之一作为Target提示。重复地,向该智能体连续显示两个提示,从可能的四个提示中随机选择,然后是一个Response提示,其中如果Target提示是该对的一部分,智能体必须响应1,否则返回0。正确的响应产生的奖励为1.0,而错误的响应返回的奖励为-1.0(这是两种选择的强制选择任务:始终产生1或0的响应)。此过程在回合的持续时间内进行迭代,即200个时间步骤。这些提示是20位的二值矢量,在每个回合的开头随机生成。为了防止采用简单的时间锁定调度策略,随机插入可变数量的零输入时间步骤,包括每次Go提示后至少有一个;作为结果,每次试验的时间长短不一,每个回合的试验次数有些变化(每个回合的平均试验次数为15)。
该结构是一个简单的循环网络,在隐含的循环层中具有200个神经元。只有循环层是可塑的:输入和输出权重是不可塑的,仅具有wi,j系数。
有24个输入:用于当前提示的20个二值输入和一个提供自回合开始以来经过的时间的输入,以及用于前一时间步骤的one-hot编码响应的两个二值输入和前一个时间步骤收到的奖励的一个实值通道(根据常见的元学习实践)(Wang et al., 2016; Duan et al., 2016)。有四个输出:one-hot编码响应的两个二值输出,以及一个输出神经元,该神经元预测该回合其余部分中未来折扣奖励的总和V(t)(由我们用于元训练的A2C算法强制执行,遵循Wang et al. (2016))以及神经调节信号M(t)。两个响应输出经过softmax运算以产生响应的概率,而M(t)信号经过tanh非线性传递,而V(t)输出为纯线性输出。所有梯度均被限制在norm 7.0,这大大提高了稳定性。
训练曲线如图1所示(右; 每条曲线显示10次运行的中位数和四分位范围)。神经调节方法成功地学习了这项任务,而非神经调节网络(Miconim, 2016; Miconi et al., 2018)和不可塑性,简单的循环网络则无法学习。我们假设这种巨大的差异与输入提示的较高维度有关:正如不可调节的可塑性网络似乎优于不可塑性网络,特别是在需要记住任意高维刺激时(Miconi et al., 2018)神经调节似乎特别有助于记忆与这种任意的高维刺激的奖励关联(请参阅附录)。
为了说明神经调节的行为,我们绘制了几个试验的神经调节神经元的输出。这些图表明,神经调节以复杂的时间依赖性的方式对奖励做出反应(参见附录)。
4.2 TASK 2: MAZE NAVIGATION TASK
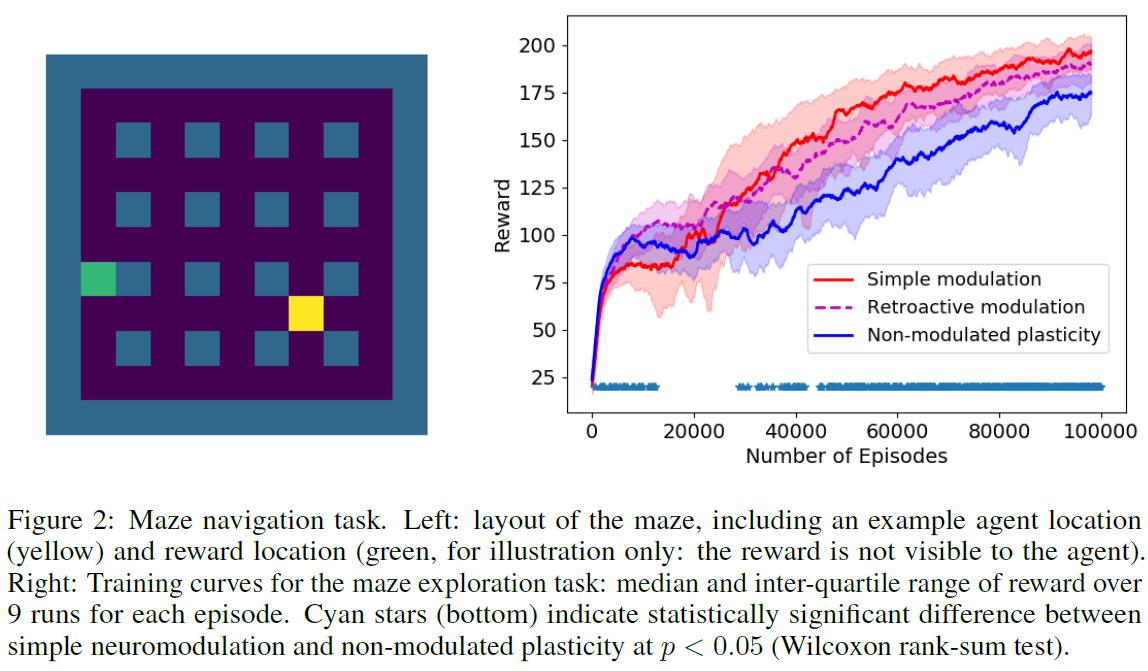
对于更具挑战性的问题,我们还对Miconi et al. (2018)提出的网格迷宫探索任务中的方法进行了测试。在此,迷宫由9 x 9个正方形组成,周围环绕着墙壁,每隔一个正方形(在任一方向上)都被墙壁占据。因此,迷宫包含16个墙正方形,除中心正方形(图2, 左)外,它们以规则的网格排列。迷宫的形状是固定的,在整个任务中不会改变。在每个回合中,随机选择一个非墙的正方形作为奖励位置。当智能体击中该位置时,它会收到奖励并立即被运送到迷宫中的随机位置。每个回合持续200个时间步骤,在此期间智能体必须累积尽可能多的奖励。奖励位置固定在一个回合内,并在各个回合之间随机分配。请注意,奖励对于智能体来说是不可见的,因此智能体仅知道通过在下一步中激活奖励输入来达到奖励位置(如果可以检测到它,可能是通过隐形传态)。
该架构与之前的任务相同,但只有100个循环神经元。输出包括通过softmax传递的4个动作通道(即,每个可能的动作中的一个:左,右,上或下),以及通过tanh非线性传递的纯线性V(t)输出和M(t)神经调节信号。智能体的输入包含一个二值矢量,该二值矢量描述了以智能体为中心的3 x 3邻域(如果相应的正方形是或不是墙壁,则将每个元素设置为1或0),以及四个用于one-got编码上一个时间步骤采取动作的额外输入,以及在上一个时间步骤获得的奖励的一个输入(按照惯例(Wang et al., 2016)。同样,只有循环权重是可塑的:输入到权重和循环到输出的权重是不可塑的。图2中的结果表明,调节方法再次优于不可调节的可塑性。
4.3 TASK 3: LANGUAGE MODELING
单词级语言建模是监督学习序列问题,目标是预测大型语言语料库中的下一个单词。语言建模需要存储长期上下文,因此LSTM模型(Hochreiter&Schmidhuber, 1997)通常在此任务上表现良好(Zaremba et al., 2014)。该实验的目的是研究为LSTM增加可塑性和神经调节作用的好处。
Penn Tree Bank语料库(PTB)是语言建模的知名基准(Marcus et al., 1993),此处用于比较不同的模型。数据集由929k训练词,73k验证词和82k测试词组成,词汇量为10k。
对于此任务,我们在两种不同的模型中实现了神经调节可塑性:从Zaremba et al. (2014)得到的具有480万个参数的基本模型,以及具有2420万个参数的更大且更复杂的模型(来自Merity&Socher (2017))。较小的模型允许进行更多的实验,而较大的模型则展示(在撰写本文时)具有最新性能的复杂模型上的神经调节结果。
附录中提供了详细的实验说明,总结如下:对于基本模型,每个网络都包含一个嵌入层,然后是两个LSTM层(大小约为200)。调整LSTM层的大小,以确保在所有实验中可训练参数的总数保持恒定;注意,这包括所有与可塑性有关的额外参数,即αi,j以及与神经调节有关的额外参数(请参阅附录)。最后一层是大小为10k的softmax层。在整个时序反向传播过程中,网络将展开20个时间步骤(Werbos, 1990)。梯度的范数固定为5。此设置类似于Zaremba et al. (2014)描述的非正则化模型。一个区别是,这里的网络权重增加了一个额外的L2惩罚(添加此惩罚始终会改进所有模型的结果)。
如(Merity&Socher, 2017)中所述,大型模型包含一个尺寸为400的嵌入,随后是三个LSTM,分别具有1150、1150和400个细胞(对于可塑版本,我们将其减小为1149、1149和400确保可训练参数的总数不高)。重要的是Merity&Socher (2017)使用了多种正则化技术。例如,训练过程涉及在多个时期之后从标准SGD切换到Averaged-SGD。与Merity&Socher (2017)的主要不同之处在于,由于计算限制,我们不实施循环随机失活(保留前馈随机失活),并且将批大小减小到7。其他超参数按原样使用,无需任何调整。有关详细信息,请参见附录。
在此评估了较小模型的四个版本(表1)。(1) 基准LSTM模型(在上段中进行了描述)1。(2) 具有不同可塑性的LSTM:每个LSTM节点中有四个循环连接,此处,根据等式1和2将可塑性添加到其中一个(有关详细信息,请参见A.1)。因为可塑性连接的数量很大,所以每个可塑性连接都有其自己单独的η,因此可以通过反向传播分别调整它们的值。(3) 具有简单神经调节作用的LSTM:这里根据等式3引入简单神经调节作用。参数η由神经元的输出M(t)代替。M(t)本身接收隐含层激活的加权组合作为输入,其中权重以通常的方式学习。每个LSTM层都有一个M(t)。(4) 具有追溯神经调节功能的LSTM:此模型与具有简单神经调节功能的LSTM相同,不同之处在于它使用的公式可以进行资格迹(等式4和5)。附录中描述了可塑性和神经调节可塑性LSTM的额外详细信息。
对于这四个模型中的每一个,我们都使用同等功率的网格搜索分别搜索了最优超参数。然后,每个模型以其最优超参数设置运行16次。表1中列出了这16个运行的平均测试困惑度以及95%的置信区间。结果表明,向LSTM添加可微的可塑性能够提供比基准LSTM稍微但统计学显著的更好结果(Wilcoxon秩和检验,p = 0.0044)。进一步(且统计学显着)增加神经调节可降低LSTM之上具有不同可塑性的困惑(p = 1e-6)。总体而言,与基准LSTM相比,追溯性神经调节可改进约1.7的困惑(统计学意义,p = 1e-7)。追溯性神经调节(即具有资格迹)确实优于简单的神经调节,但在传统的p < 0.05截止(p = 0.066)时,改进几乎没有统计学意义。请注意,尽管这些数字与最新的结果(使用相当大且更复杂的架构)相去甚远,但它们仍然都比使用类似架构的已发表工作要好(Zaremba et al., 2014)。
对于较大的模型,我们比较了一个版本,在该版本中,已重新实现核心LSTM模块以具有神经调节的可塑性连接(仅简单的神经调节;未实现追溯调节),以及使用相同LSTM重新实现但没有可塑性和调节性的基准模型,以使比较尽可能地相等。请注意,在此模型中,可塑性系数归因于"每个神经元":每个神经元αi仅有一个 i (而不是每个连接一个),该值适用于传入该神经元的所有连接的赫布迹。这有助于限制参数的总数。有关更完整的说明,请参见附录。调节后的可塑模型相对于不可塑模型(表1)显示出较小的改进,证实了使用较小模型获得的结果。

1 由于我们进行了超参数调整,因此基准LSTM性能优于(Zaremba et al., 2014)中发布的性能,如附录中所述。
5 DISCUSSION AND FUTURE WORK
本文介绍了一种以生物学为灵感的方法来训练网络以自我调整其权重。基于可微的可塑性框架,该框架已经在各种监督和RL任务上比不可塑架构提高了性能(有时显著)(Miconi, 2016; Miconi et al., 2018),在此我们引入神经调节可塑性,以使网络控制其自己的权重变化。作为结果,神经调节可塑性网络首次可以通过梯度下降进行训练,从而为优化大规模自修改神经网络开辟了新的研究方向。
作为对所研究的简单RL域的好处的补充,我们发现可塑且神经调节的LSTM在基准语言建模任务(重要的是LSTM应用的中心领域)方面优于标准LSTM,这潜在地非常重要。LSTM用于具有大量学术和经济影响的实际应用中。因此,如果可塑且神经调节的作用持续改进LSTM性能(对于固定的搜索空间大小),则潜在的好处将是可观的。我们打算继续进行这方面的研究,并就其他LSTM常用的问题(例如预测)对可塑LSTM(神经调节和非神经调节的)进行测试。
从概念上讲,一个重要的比较点是Wang et al. (2016; 2018)引入的"学会强化学习"(L2RL)框架。在这种元学习框架中,权重在回合期间不会改变:所有回合内学习都是通过更新网络的活动状态来进行的。该框架被明确描述(Wang et al., 2018),是基于奖励的多巴胺系统缓慢塑造前额叶皮层的模型,类似于用于元训练的A2C算法功能(例如价值信号的使用和权重的调节会因奖励预测误差而发生变化)。如上面的RL实验中所述,我们的方法通过允许系统存储状态信息(除了隐含状态更改之外),还增加了权重更改,从而为该模型增加了更多灵活性。但是,由于我们的框架允许网络更新其自身的连接性,因此我们可能会将L2RL模型扩展到一个更高的水平:系统现在可以确定自己的任意属性,而不必将A2C用作手工设计的基于奖励的权重修改方案。权重修改方案,可以利用它可以计算的任何信号(奖励预测,惊喜,显著性等)。这种新兴的权重修改算法(通过"外环"元训练算法在许多回合/一生中设计)可能会进而塑造网络连接以实现Wang et al. (2018)描述的元学习过程。重要的是,这种额外的学习水平(或"元-元学习")不仅仅是纯粹的幻想:它无疑是在进化中发生的。因为人类(和其他动物)可以在其一生中进行元学习("学会学习")(Harlow, 1949; Wang et al., 2018),并且因为人类本身就是优化过程的结果(进化),那么元-元学习不仅发生了,而且可能是人类某些最高级的心理功能的关键。我们的框架为研究此过程提供了诱人的可能性,同时允许我们在最外面的优化循环中用任何基于梯度的方法来替代进化。
为了研究我们方法的全部潜力,上述框架需要进行一些改进。其中包括:实现多种神经调节信号(每个都有自己的输入和输出),在大脑中似乎就是这种情况(Lammel et al., 2014; Howe&Dombeck, 2016; Saunders et al., 2018);引入更复杂的任务,可以充分利用框架的灵活性,包括追溯性调节提供的资格迹以及上述若干学习水平;并解决通过奖励调节的赫布可塑性实现强化学习的陷阱(例如,赫布学习的无监督部分与基于奖励的修改之间的内在干扰;Frémaux et al., 2010; Frémaux&Gerstner, 2015),以促进高效且自成体系的RL系统的自动设计。最后,可能有必要允许元训练算法设计系统的整体结构,而不是简单地设计固定的手工设计结构的参数。具有如此巨大的扩展潜力,我们的神经调节可塑网络框架为激动人心的研究开辟了许多途径。
A APPENDIX
A.1 PLASTIC LSTMS: BASIC MODEL
A.1.1 ADDING PLASTICITY TO LSTMS
每个LSTM节点均包含通过它的四个加权循环路径it, jt, ft和ot,如以下等式所示:
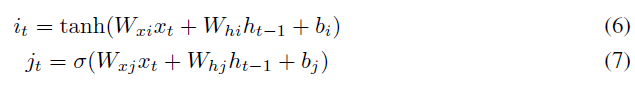
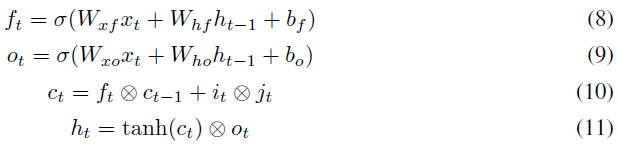
jt,ft和ot用于控制通过LSTM的数据流,it是实际数据。因此,在通过it的路径中引入了可塑性(将可塑性添加到LSTM的控制路径中是为了将来的工作)。相应的突触前后激活(分别在等式1和2中表示为xi(t-1)和xj(t))是ht-1和it。大小为200的一层具有40k (200x200)个可塑性连接。每个可塑性连接都有自己个人的η(在等式2中使用),可以通过反向传播来学习。可塑性系数(αi,j)如等式1所示使用。
A.1.2 ADDING NEUROMODULATION TO LSTMS
如等式3所示,对于简单的神经调节,将其替换为网络计算的神经元的输出M(t)。对于经过神经调节的LSTM,每个可塑性连接的单独η都被神经元的输出(M(t))所替代,该输出的扇出量等于可塑性连接的数量。该神经元的输入是上一时间步骤的层的激活ht-1。每个LSTM层都有其专用的神经调节神经元。此设置的其他变体包括每个节点有一个专用的神经调节神经元,或者整个网络都有一个神经调节神经元。初步实验表明,这些变化的表现较差,因此未作进一步评估。
A.2 MORE DETAILS FOR LANGUAGE MODELING EXPERIMENT
表1所示的所有四个模型都使用SGD进行了训练。初始学习率设置为1.0。每个模型训练了13个epoch。LSTM的隐含状态被初始化为零;当前迷你批处理的最终隐含状态用作后续迷你批处理的初始隐含状态。
对四个超参数执行了网格搜索:(1) 学习率衰减因子在0.25到0.4的范围内,以0.01为步长。(2) 学习率衰减在-{4, 5, 6}范围内开始的epoch。(3) 权重的初始比例在-{0.09, 0.1, 0.11, 0.12}范围内。(4) L2惩罚常数在{1e-2, 1e-3, 1e-4, 1e-5, 1e-6}范围内。
A.3 LARGE WORD-MODELLING NETWORK
除了先前的模型外,我们还将Backpropamine框架应用于Merity&Socher (2017)所描述的更大且最新的模型中。该模型由三个堆叠的LSTM组成,每个LSTM分别具有115、1150和400个细胞,输入嵌入的大小为400,输出softmax层与输入嵌入共享权重。该模型利用了许多优化和正则化技术。连续的LSTM之间的连接实现了"变分"随机失活,其中在整个前向和后向传递Gal & Ghahramani (2016)中使用通用随机失活掩码。通过时序反向传播使用以70个词为中心的可变范围。45个epoch后,优化器从SGD(无动量)切换到Averaged-SGD,这包括计算标准SGD步骤,但取所得的连续更新权重向量的均值。这完全符合Merity&Socher (2017)的规定。唯一的不同是,我们没有在循环连接中实现权重下降,对于所有模型的所有运行,都在45个epoch强制切换到ASGD,并且由于计算限制而将批大小限制为7。
可塑性系数归因于"每个神经元":每个神经元 i 而不是每个连接具有独立的αi,j,而是将可塑性系数αi应用于其所有传入连接(请注意,对于每个连接,赫布迹Hebbi,j仍单独维护)。这减少了可训练参数的数量,因为它现在是长度为N的向量,而不是大小为N x N的矩阵(其中N是循环神经元的数目)。
我们执行如等式3中所述的简单神经调节。具有tanh非线性的单个神经调节器神经元接收来自所有循环神经元的输入。然后,使该神经调节剂输入通过权重向量(每个神经元一个),为每个神经元产生不同的ηi。换句话说,不同的神经元 i 具有不同的ηi,但是这些都是共同值的固定倍数。这是一个中间解决方案,介于整个网络只有一个η(t)和为每个神经元独立计算一个独立的ηi,每个神经元都有自己的输入权重(这需要N x N权重,而不是当前解决方案的2 x N权重)。对模型中的三个LSTM分别进行神经调节。
对于不可塑网络,可训练参数的总数为24221600。对于神经调节可塑版本,我们将LSTM中的隐含细胞数从1150减少到1149,足以将参数总数减少到24198893个可训练参数(而不是1150个细胞的LSTM的24229703)。
所有其他超参数均取自Merity&Socher (2017),使用其代码库中提供的有关其模型的说明,该说明可从https://github.com/salesforce/awd-lstm-lm获取。由于计算限制,我们没有执行任何超参数调整。
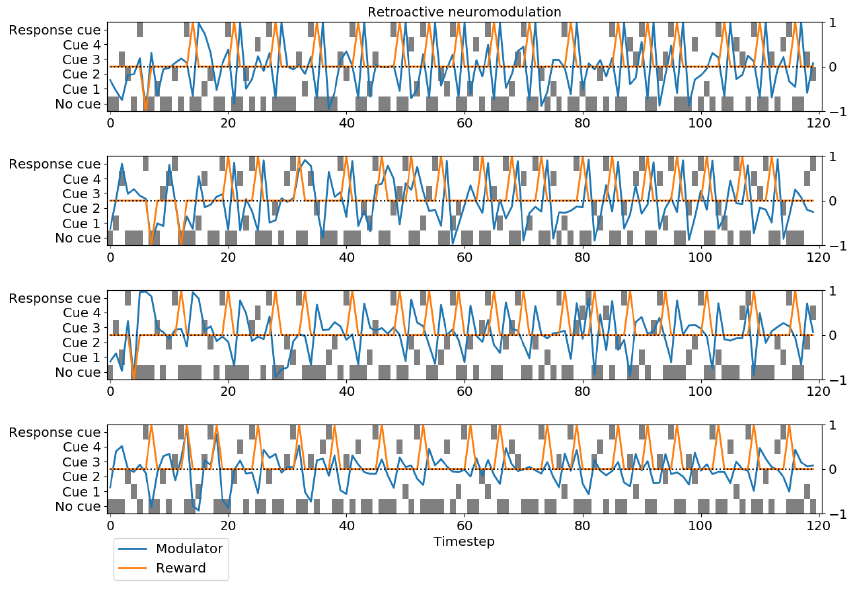

图3:神经调节的动力学。对于简单调节和追溯调节,我们展示了4个运行中每个运行的一个试验。在每个时间步骤处,灰色方块指示显示了哪个提示。橙色曲线表示上一个时间步骤(即当前馈入网络的时间步骤)的奖励,始终为-1、0或1;蓝色曲线表示当前时间步骤的调节器输出值。注意动态的多样性。
A.4 DYNAMICS OF NEUROMODULATION
为了说明神经调节的行为,我们绘制了任务1的多次运行进行随机试验的神经调节神经元的输出(图3)。所有的运行都来自训练有素且非常成功的网络,负奖励的比例很低,可以看出这一点。对于每次运行,我们都绘制了每个时间步骤的神经调节剂输出值以及网络当前正在感知的奖励(即前一时间步骤的响应所产生的奖励)。
这些图揭示了丰富且复杂的动态,在每次运行之间差异很大。调节神经元显然对奖励做出反应;然而,该反应是复杂且随时间变化的,并且每次运行都不同。追溯调节的最高运行趋向于响应正奖励而产生负神经调节,反之亦然;对于简单的神经调节,倒数第二个运行趋向于相反。一种常见的模式是在奖励感知之后的时间步骤上产生负神经刺激(特别是对于简单的神经调节)。追溯调节的运行中有两个表现出一种模式,其中奖励感知之后是高度正神经调节,然后是高度负神经调节。理解这些复杂的动态机制进行有效的回合内学习的机制是未来工作的重要方向。
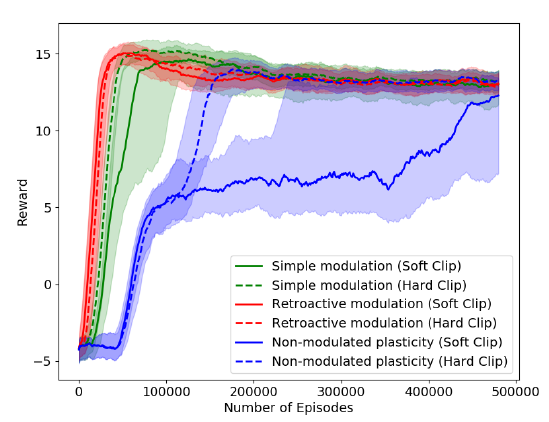
图4:具有固定的二值四位线索(中位数和四分之三的每个回合超过10次运行的奖励范围)的线索-奖励关联任务的训练曲线。"软裁剪"是指等式2中使用的不同裁剪操作;"硬裁剪"与本文中使用的相同,即"方法"中描述的简单裁剪。请注意,不可调节可塑性网络可以成功解决此任务。
A.5 CUE-REWARD ASSOCIATION TASK
在上述提示-奖励关联学习任务中,神经调节可塑性能够学习非调节可塑性根本无法完成的任务。这种差异的根源可能是什么?在先前的实验中,我们实现了相同的任务,但整个任务仅使用了四个固定的4位二值提示,即'1000','0100','0010'和'0001'。在此任务的简化版本中,无需记住每个回合的线索,并且每个回合唯一要学习的是四个已知线索中的哪个与奖励相关联。这与以上论文中使用的版本形成对照,后者中的提示是为每个回合随机生成的任意20位向量。使用固定的四位提示,非调节可塑性能够学习任务,尽管比神经调节可塑性要慢一些(见图4)。
这表明神经调节可塑性比非调节可塑性具有更强的优势,特别是在要学习的联想涉及任意高维度线索的情况下,必须将其与联想本身一起记忆。这与Miconi et al. (2018)的结果相呼应,他提出在需要快速存储高维输入的任务上,可塑性网络的性能要优于不可塑网络(例如(Miconi et al., 2018)中的图像存储和重建任务)。
显然,需要更多的工作来研究哪些问题比不可调节或不可塑方法最受益于神经调节的可塑性。我们打算在以后的工作中继续进行这一研究。



