Meta-Learning through Hebbian Plasticity in Random Networks
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, Canada.
Abstract
终生学习和适应能力是生物智能体的两个定义方面。现代RL方法已显示出在解决复杂任务方面的重大进步,但是,一旦训练结束,找到的解决方案通常是静态的,并且无法适应新的信息或干扰。尽管仍不能完全理解生物大脑如何从经验中学习和有效适应,但据信突触可塑性在此过程中起着重要作用。受到这种生物学机制的启发,我们提出了一种搜索方法,而不是直接优化神经网络的权重参数,而仅搜索突触特定的赫布学习规则,该规则使网络可以在智能体的生命周期内不断地自组织其权重。我们展示了在几种具有不同感觉方式和超过450K个可训练的可塑性参数的RL任务中的方法。我们发现,从完全随机的权重开始,发现的赫布规则使智能体能够在动态2D像素环境中导航。同样,它们可以使模拟的3D四足机器人在不超过100个时间步骤的情况下学会如何行走,并能适应训练期间未见的形态损伤以及没有任何明确奖励或错误信号的情况。代码可以在此获取:https://github.com/enajx/HebbianMetaLearning。
PS:对源代码的分析参见https://www.cnblogs.com/lucifer1997/p/14681645.html。
1 Introduction
已经证明,由神经网络控制并通过RL训练的智能体能够解决复杂的任务[1-3]。但是,一旦经过训练,这些智能体的神经网络权重通常是静态的,因此它们的行为大部分保持僵化,显示出对看不见的条件或信息的适应性有限。这些解决方案,无论是通过基于梯度的方法还是通过黑盒优化算法找到的,通常都是不可变的,并且对于它们经过训练可以解决的问题过于具体[4, 5]。当将这些网络应用于其他任务时,需要对其进行重训练,这需要进行许多额外的迭代。
与人工神经网络不同,生物智能体表现出显著水平的适应性行为并且可以快速学习[6, 7]。尽管尚未完全理解其潜在机制,但已充分确定突触可塑性起着基本作用[8, 9]。例如,许多动物出生后可以快速行走,而无需任何明确的监督或奖励信号,可以无缝地适应其原产地。已经提出了不同的可塑性调节机制,这些机制可以包含在两个主要的理想类型族中:涉及自上而下的反馈传播误差的端到端机制[10],以及仅依赖于局部活动来调节突触连接的动态的局部机制。最早提出的纯局部机制的版本被称为赫布可塑性,它以最简单的形式表明神经元之间的突触强度与它们之间的活动相关性成比例地变化[11]。
非可塑性网络的刚性及其一旦训练就无法继续学习的部分原因可归因于它们传统上既具有固定的神经结构又具有一组静态的突触权重。因此,在这项工作中,我们对寻找可塑性机制的算法感兴趣,这些机制可让智能体在其一生中适应[12-15]。尽管该领域的最新工作集中在确定网络的权重和可塑性参数上,但随机初始化的网络在机器学习[16-18]和神经科学[19]中的有趣特性特别吸引我们。因此,我们提出仅基于自组织过程来搜索可用于随机初始化网络的可塑性规则。
为此,我们针对连接特定的赫布学习规则进行了优化,该规则允许智能体为非平凡的RL任务找到高性能的权重,而在其生命周期中无需任何明确的奖励。我们演示了在两个连续控制任务上的方法,并表明在基于视觉的RL任务中,这种网络比固定权重的网络具有更高的性能。在3-D运动任务中,赫布网络能够适应训练过程中未发现的模拟四足机器人的形态损伤,而固定权重网络则无法做到。与固定权重网络相反,赫布网络的权重在智能体的生存期内不断变化。进化的可塑性规则导致在权重相位空间中出现吸引子,这导致网络迅速收敛到高性能动态权重。
我们希望,我们对随机赫布网络的演示将激发神经可塑性方面的更多工作,这些工作将挑战当前在RL中的假设。我们提倡使用更具动态性的神经网络,而不是使用经过微调和冻结的权重开始部署智能体,这样可以显示更接近其生物学对应物的动态性。有趣的是,我们发现找到的赫布网络非常鲁棒,甚至可以从将其大部分权重清零后恢复。
在本文中,我们着重于探索赫布可塑性在掌握RL问题方面的潜力。同时,ANN已经成为神经科学家感兴趣的对象,因为它能够解释一些神经生物学数据[20],同时能够在人的层面上执行某些视觉认知任务。同样,演示通过局部规则进行单独优化的随机网络如何能够在复杂任务中达到竞争性能,可能有助于建立合理的模型库,以了解大脑中的学习方式。最后,我们希望这一系列研究将进一步帮助促进基于ANN的RL框架,以研究生物智能体的学习方式[21]。
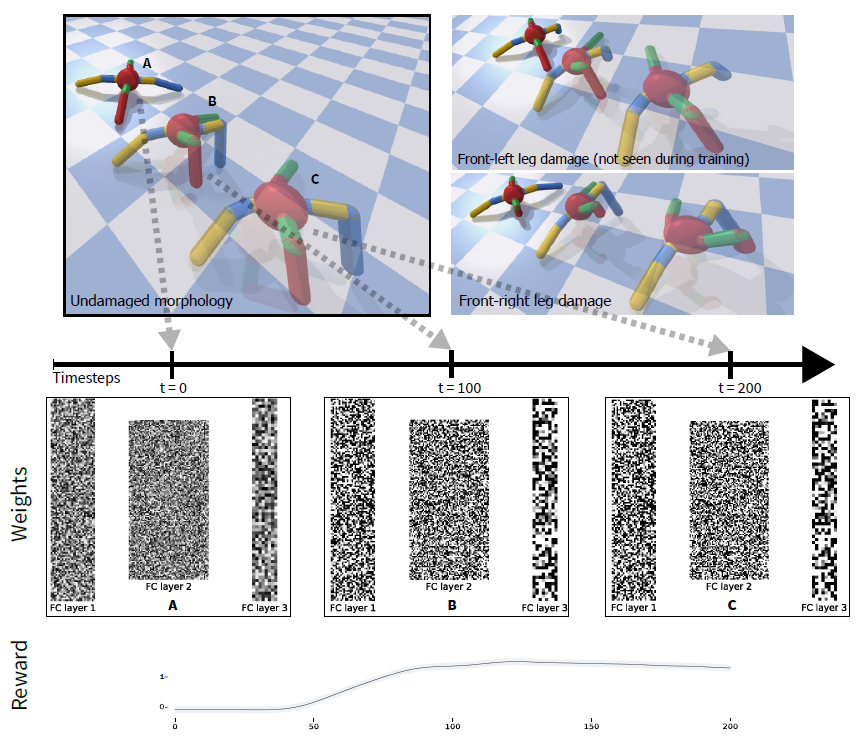
图1:随机网络中的赫布学习。从随机权重开始,发现的学习规则可以快速适应不同的形态损伤,而无需明确的奖励信号。该图显示了具有标准形态的机器人在生命周期中三个不同时间步骤(A, B, C)的网络权重(左上)。每列表示不同时间步骤下每个网络层的权重。在t = 0 (A)时,通过从均匀分布w ∈ U[-0.1, 0.1]中进行采样来随机初始化网络的权重,然后根据进化的赫布规则和来自环境的感官输入确定其动态。经过几步后,四足动物开始移动,这反映出回合奖励的增加(下行)。具有相同赫布规则的网络能够适应具有不同形态损伤的机器人,即使是在训练过程中未见过的机器人(右上)。
2 Related work
Meta-learning. 元学习或学会学习[22, 23]的目标是创建可以从持续的经验中快速学习的智能体。元学习已有多种不同的方法[24-29]。例如,Wang等人[27]表明,一个循环LSTM网络[30]可以学会强化学习。在他们的工作中,策略网络连接在智能体的生命周期中保持不变,并且通过更改LSTM的隐含状态来实现学习。虽然大多数方法,例如Wang等人的工作[27],将环境的奖励作为元学习算法的内环中的输入(作为对神经网络的输入或调整网络的权重),但在此工作中,我们在智能体生命周期中没有给出明确的奖励。
通常,在元训练期间,对网络进行许多不同任务的训练,然后对它们学习新任务的能力进行测试。元学习的最新趋势是找到良好的初始权重(例如,通过梯度下降[28]或演变[29]),可以通过几次迭代来进行自适应。一种这样的方法是与模型无关的元学习(MAML)[28],它允许模拟机器人快速适应不同的目标方向。混合方法将基于梯度的学习与无监督的赫布规则结合在一起,也已被证明可以提高监督学习任务的性能[31]。
较少研究的元学习方法是可塑性网络的演变,该网络在各种时间尺度上都会发生变化,例如在经历感觉反馈的同时,它们的神经连通性也会发生变化。这些不断进化的可塑性网络受发现神经适应,学习和记忆原理的希望而启发[13]。它们使智能体能够在生命周期内通过不断进化的可存储激活模式的循环网络进行适应[32]或通过进化形式的局部赫布学习规则来进行一种元学习,该规则基于神经元的相关激活来改变网络的权重("共同发放的神经元连接在一起")。早期的工作[14]没有依靠赫布学习规则,而是尝试探索适用于网络中所有连接的参数化学习规则的参数优化。与我们的方法最相关的是Floreano和Urzelai [33]的早期工作,他们探索了使用随机权重启动网络然后应用赫布学习的想法。这种方法展示了不断进化的赫布规则的希望,但仅限于四种不同类型的赫布规则和应用于简单机器人导航任务的小型网络(12个神经元,144个连接)。
代替通过进化优化来训练局部学习规则,最近的工作表明,也可以通过梯度下降来优化单个突触连接的可塑性[15]。但是,尽管可训练参数的工作仅决定每个连接的可塑性,但本文采用的黑盒优化方法允许每个连接实现自己的赫布学习规则。
Self-Organization. 自组织在许多自然系统中都起着至关重要的作用[34],并且是复杂系统研究的活跃领域。最近,它在机器学习中也越来越突出,图神经网络就是一个值得注意的例子[35]。Mordvintsev等人最近的工作[36]关于通过神经网络编码的局部规则来发展元胞自动机,与我们在此提出的工作有相似之处。在他们的工作中2D图像的发展依赖于自组织,而在我们的工作中,网络的权重本身就是自组织的。自组织系统的好处是它们非常鲁棒和自适应。我们提出的方法的目标是朝基于神经网络的RL智能体的相似级别的鲁棒性迈出一步。
Neuroscience. 在生物神经系统中,通过突触可塑性减弱和增强突触被认为是长期学习的关键机制之一[8, 9]。进化在很长的时间范围内塑造了这些学习机制,从而使我们的生活变得高效。清楚的是,大脑可以根据我们一生的经历重新进行自我连接[37]。此外,动物的出生具有高度结构化的大脑连通性,这使它们能够从出生开始就快速学习[38]。然而,人们对生物大脑中随机连接的重要性的了解还很少。例如,随机连通性似乎在前额叶皮层中起着至关重要的作用[39],从而增加了神经表征的维度。有趣的是,直到最近才表明,当随机网络与简单的赫布学习规则结合时,这些理论模型与实验数据更好地匹配[19]。
在生物脉冲网络中发生的最著名的突触可塑性形式是脉冲时序依赖可塑性(STDP)。另一方面,人工神经网络具有连续输出,通常将其解释为脉冲网络的抽象形式,其中每个神经元的连续输出代表长时间窗口内的单独神经元(或等效的短时间窗口内的脉冲神经元子集)的脉冲发放率编码均值,而不是脉冲时序编码;在这种情况下,突触前和突触后活动的相对时序不再发挥中心作用[40, 41]。脉冲发放率依赖可塑性(SRDP)是生物大脑中有充分文献记载的现象[42, 43]。我们从这项工作中获得了启发,表明随机网络与赫布学习相结合也可以实现更强大的元学习方法。
3 Meta-learning through Evolved Local Learning Rules
我们的方法的主要步骤可以概括如下:(1) 创建具有随机突触特定学习规则的初始神经网络种群;(2) 使用随机权重初始化每个网络,并根据任务的累积回合奖励对其进行评估,网络权重随发现的学习规则而在每个时间步骤变化,并且(3) 通过进化策略[44]创建新的种群,将学习规则参数向具有更高累积奖励的规则移动。然后,算法再次从(2)开始,目标是逐步发现越来越多的有效学习规则,这些规则可以与任意初始化的网络一起使用。
更详细地讲,本文中针对突触的学习规则是受生物学的赫布机制启发的。我们使用广义赫布ABCD模型[45, 46]来控制相对简单前馈网络的人工神经元之间的突触强度。具体来说,智能体的权重会在其生存期内的以下每个时间步骤中随机初始化和更新:
![]()
其中wij是神经元 i 和 j 之间的权重,ηw是进化学习率,进化相关项Aw,进化突触前项Bw,进化突触后项Cw,oi和oj分别是突触前和突触后激活。虽然系数A, B, C明确确定了网络权重的局部动态,但进化系数D可以被解释为网络中每个连接的单个抑制/兴奋性偏差。与以前的工作相比,我们的方法不仅限于统一的可塑性[47, 48](即每个连接具有相同的可塑性),也不受限于仅优化连接特定的可塑性值[15]。取而代之的是,基于最近的进化策略实现可扩展到大量参数的能力[44],我们的方法允许网络中的每个连接都具有不同的学习规则和学习率。
我们假设这种赫布可塑性机制应该在权重相位空间中引起吸引子的出现,这会导致策略网络的随机初始化权重在环境感官反馈的引导下迅速收敛到高性能值。
3.1 Optimization details
我们采用的基于种群的优化算法是一种进化策略(ES)[49, 50]。与其他深度RL方法相比,ES在各种不同任务上的竞争能力最近有所提高[44]。这些黑盒优化方法的优点是不需要反向传播梯度,并且可以处理稀疏奖励和密集奖励。在此,我们采用Salimans等人的ES算法[44],不直接优化权重,而是根据环境的输入找到一组赫布系数,以在网络生命周期内动态控制网络的权重。
为了制定最优的局部学习规则,我们分别通过从均匀分布w ∈ U[-0.1, 0.1]和h ∈ U[0, 1]中采样来随机初始化策略网络的权重w和赫布系数h。随后,我们让ES算法进化h,进而通过等式1确定每个时间步骤对策略网络权重的更新。
在每个进化步骤 t 上,我们计算智能体F(ht)的任务相关适应性,通过采样正常噪声εi = N(0, 1)并将其添加到当前最优解决方案ht中,填充一组新的n个候选解决方案ht,随后我们基于i ∈ n个候选解决方案中每一个的适应性评估来更新解决方案的参数:
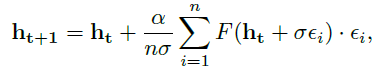
其中α调节每一代更新多少参数,σ调节候选解决方案中引入的噪声量。重要的是要注意,智能体在其一生中无权获得此奖励。
我们将赫布方法与标准固定权重方法进行比较,使用相同的ES算法分别直接优化权重或学习规则参数。https://github.com/enajx/HebbianMetaLearning提供了使用ES算法进化赫布网络和静态网络所需的所有代码。

4 Experimental Setups
我们在具有不同感官模式的两个连续控制环境中展示了我们的方法(图2)。第一个是具有挑战性的基于视觉的RL任务,其目标是尽可能快地使赛车驶过程序生成的轨道。尽管看起来不太复杂,但任务只是在最近才解决(在100次随机部署中,平均得分超过900分)[52-54]。第二个领域是控制四足机器人的复杂3D运动任务[55]。在此,环境信息被表示为一维状态向量。
Vision-based environment 作为基于视觉的环境,我们使用由Box2D物理引擎构建的CarRacing-v0域[51]。对环境的输出状态进行调整以及归一化,从而形成了3个通道(RGB)的观察空间,每个通道的84 x84像素。该策略网络由两个卷积层组成,由双曲正切激活,并由池化层插入(3层前馈网络每层分别有[128, 64, 3]个节点,无偏差)。该网络具有92690个权重参数,其中1362个对应于卷积层,而91328个对应于全连接层。三个网络输出控制三个连续动作(左/右转向,加速,中断)。在ABCD机制下,这导致了456640个Hebbian系数,包括终生学习率η。
在这种环境中,只有全连接层的权重受赫布可塑性机制控制,而卷积层的1362个参数在智能体的生命周期内保持静态。原因是,对于卷积滤波器的突触前和突触后活动可能没有什么自然定义,因此使对卷积层的赫布可塑性的解释具有挑战性。此外,先前对人类视觉皮层的研究表明,腹侧流早期区域中视觉刺激的表征与训练用于图像识别的卷积层的表征兼容[56],因此表明卷积层参数的可变性应受到限制。进化适应度计算为每帧-0.1,访问的每个轨道图块为+1000/N,其中N是所生成轨道中图块的总数。
3-D Locomotion Task 对于四足动物,我们使用一个三层前馈网络(每层具有[128, 64, 8]个节点,无偏差,激活函数为双曲正切)。这种架构选择导致具有12288个突触的网络。在ABCD可塑性机制下,每个突触具有5个系数,这转化为包括终生学习率η在内的61440个Hebbian系数集。对于状态向量环境,我们使用开源的Bullet物理引擎及其pyBullet python包装器[57],其中包括"蚂蚁"机器人,具有13个刚性连杆的四足动物(包括四个腿,一个躯干以及8个关节)[58]。它是根据MuJoCo仿真器[59]中的蚂蚁机器人建模的,并构成了RL [28]中的通用基准。机器人的输入大小为28,包括智能体的位置和速度信息以及8个维度的动作空间,用于控制8个关节中每个关节的运动。四足智能体的适应度函数选择沿固定轴的1000个时间步骤内的行进距离。
用于ES算法以优化赫布网络和静态网络的参数如下:CarRacing-v0域的种群大小为200,四足动物的种群大小为500,反映了该域的更高复杂性。其他参数对于这两个域都是相同的,并且反映了典型的ES设置(与其他RL方法相比,ES算法对不同的超参数通常更鲁棒[44]),学习率α=0.2,α衰减=0.995,σ=0.1和σ衰减=0.999。这些超参数是通过反复试验发现的,并且在先前的实验中效果最佳。
PS:参考源代码,通过进化策略最终学到的赫布规则能够找到状态与动作之间的对应关系(即策略),每个动作与输出层神经元一一对应。
4.1 Results
对于这两个域的每一个,我们针对静态方法和赫布方法进行了三个独立的进化过程(具有不同的随机种子)。我们对广义赫布规则的受限形式进行了其他消融研究,可在附录中找到。
Vision-based Environment 为了测试改进的解决方案的总体推广效果,我们比较了性能最高的基于赫布的方法和传统的固定权重方法在100次部署中平均获得的累积奖励。ES算法发现的一组局部学习规则产生的奖励为872±11,而静态权重解决方案的性能仅为711±16。赫布网络的数量略低于该领域最新方法的性能,该方法依赖于其他神经注意力机制(914±15 [54]),但与诸如PPO之类的深度RL方法相提并论(865±159 [54])。赫布学习智能体的可比性能令人惊讶,因为它以完全不同的随机权重启动100个部署中的每一个,但是通过调整后的学习规则,它能够快速适应。虽然赫布网络需要稍长的时间才能达到较高的训练效果,这可能是由于参数空间的增加(请参阅附录),但是,如果在训练过程中看不到的程序生成的轨道上进行测试,则好处是通用性更高。
3-D Locomotion Task 对于运动任务,我们创建了四足机器人的三个变体,以模拟对其一只腿进行部分损坏的效果(图2)。这些形态的选择旨在创建一个任务,对于无法适应的神经网络来说,这是很难掌握的。在训练过程中,静态权重和赫布可塑性网络都遵循相同的设置:在每个训练步骤中,策略均按照第3.1节中所述的ES算法进行优化,其中适应度函数包括两种形态的平均行走距离, 一个标准的和一个右前腿损坏的。第三形态(在左前腿上受损)被排除在训练循环之外,以便随后评估网络的泛化。
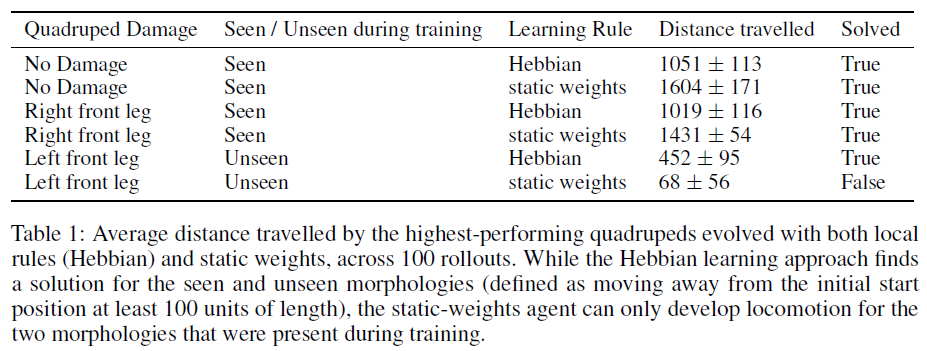
对于四足动物,我们将解决任务定义为沿固定轴单调离开其初始位置至少100个长度单位。在五次进化运行中,赫布网络和静态网络都为所有运行中的可见形态找到了解决方案。另一方面,静态权重网络无法找到可以解决看不见的损坏形态的单一解决方案,而赫布网络却确实设法找到了看不见的损坏形态的解决方案。但是,在看不见的形态上评估的赫布网络的性能差异很大。理解为什么某些赫布解决方案具有普遍性,而另一些却没有为进一步的研究铺平道路;我们假设,为了获得能够可靠泛化的解决方案,需要对具有随机损伤的多种形态进行训练。为了测试改进的解决方案的总体推广效果,我们比较了赫布网络和静态权重网络在100个部署上的平均步行距离。我们从一次进化运行中就每种形态报告了性能最高的解决方案(表1)。
由于静态权重网络无法适应环境,因此它可以有效地解决训练过程中出现的形态,但在看不见的形态下会失败。另一方面,赫布网络能够适应新的形态,从而有效地自组织网络突触权重(图1)。此外,我们发现,网络的初始随机权重甚至可以从发现赫布系数时使用的分布之外的其他分布中采样,例如N(0, 0.1),并且该智能体仍然可以达到可比的性能。
有趣的是,即使在生命周期中不存在任何奖励反馈,基于赫布的网络也能够为这三种形态中的每一种找到表现良好的权重。仅传入的激活模式就足以使网络适应,而无需明确知道当前正在模拟的形态。但是,对于静态权重网络确实能够解决的形态,它比基于赫布的方法获得了更高的奖励。可能有几个原因可以解释这一点,包括需要额外的时间来学习或参数空间更大,这可能需要更长的训练时间才能找到更有效的可塑性规则。
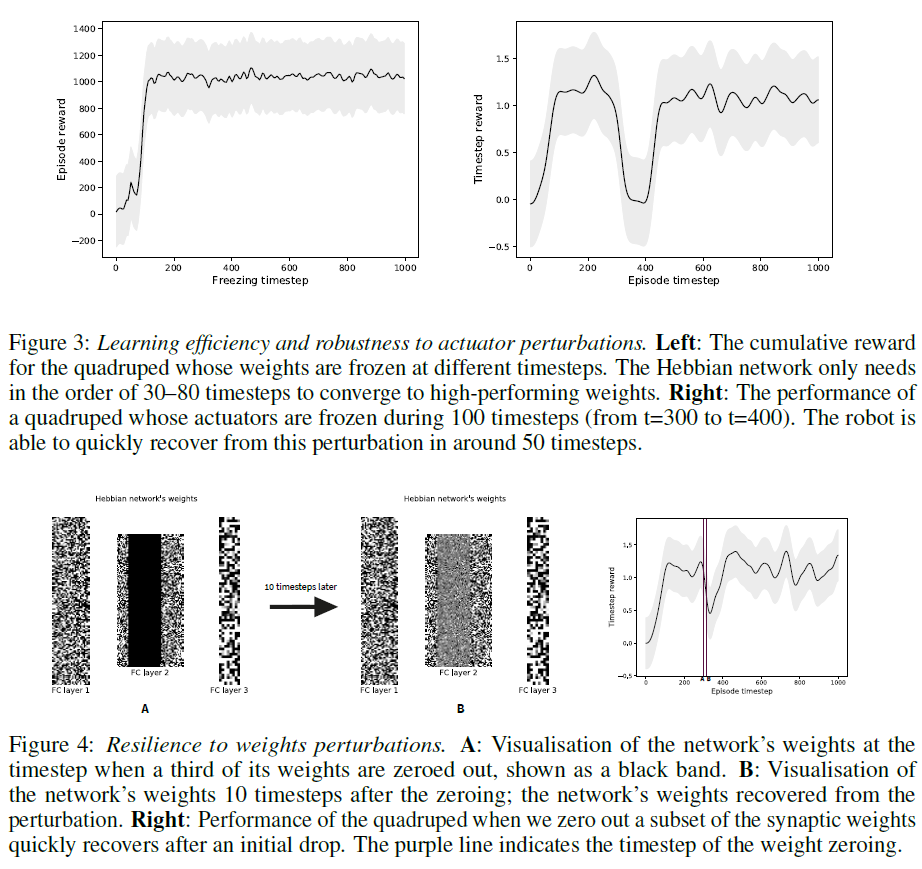
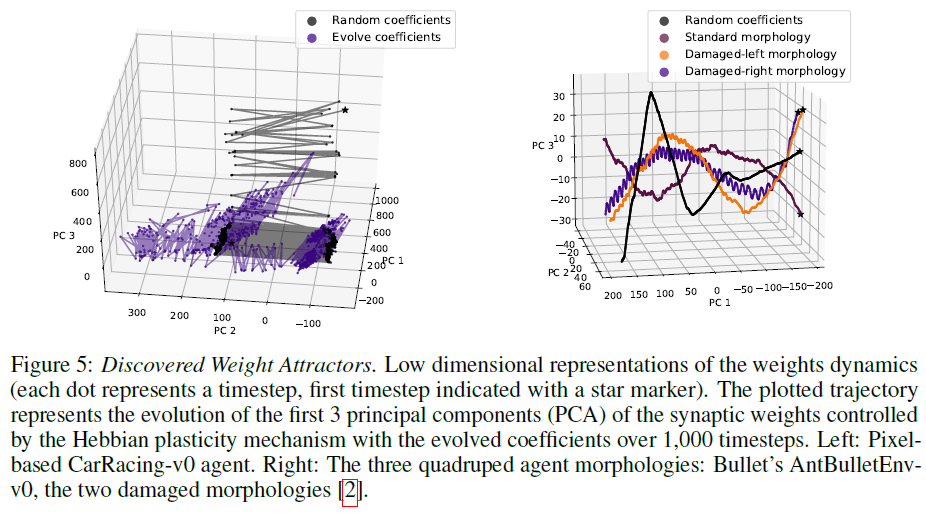
为了确定在智能体程序的生命周期内权重从随机收敛到最优所需的最小时间步骤,我们研究了在不同时间步骤后冻结权重的赫布更新机制,并检查了结果回合的累积奖励。我们观察到权重只需要30到80个时间步骤(即赫布更新)即可收敛到一组最优值(图3, 左)。此外,我们通过将网络的所有输出饱和到1.0 (100个时间步骤),测试了网络对外部干扰的恢复能力,有效地将智能体冻结在了适当的位置。图3右侧显示,经过改进的赫布规则允许网络在几个时间步骤内恢复到最优权重。此外,赫布网络能够从其连接的部分丢失中恢复,我们通过在一个时间步骤内将一部分突触权重归零来进行模拟(图4, 左)。我们观察到智能体行为的短暂中断,但是,网络能够在几个时间步骤内重新收敛到最优解决方案(图4, 右上)。
为了更好地了解发现的可塑性规则的效果以及权重模式在赫布学习期间的发展,我们通过主成分分析(PCA)进行了降维,该主成分分析投影了网络权重所在的高维空间在每个时间步骤上都以3维表示,因此大多数方差可以通过此较低维表示得到最好的解释(图5)。对于汽车环境,权重无处不在跨越缩减的PCA空间的三个主要成分,这与网络的动态形成了鲜明的对比,在网络中,我们将赫布系数(等式1)设置为随机值;这里的权重轨迹缺少任何结构,并且在零附近振荡。在三个四足形态的情况下,赫布网络的轨迹遵循具有振荡特征的3维曲线。在具有随机赫布系数的情况下,网络不会在其权重轨迹中产生任何明显的结构。
5 Discussion and Future Work
在这项工作中,我们引入了一种新颖的方法,允许具有随机权重的智能体快速适应任务。有趣的是,终生适应的发生没有任何明确提供的奖励信号,并且仅基于不断进化的赫布局部学习规则。与典型的静态网络方法相反,在传统的静态网络方法中,网络的权重在智能体程序的生命周期中不发生变化,而基于赫布的网络中的权重在它们的生命周期内自组织并收敛到权重空间中的吸引子。
快速适应权重的能力对于适应诸如受损机器人形态等任务非常重要,这对于诸如持续学习之类的任务可能很有用[60]。从最初的随机权重收敛到高性能权重的能力令人惊讶地强大,并且最优网络设法对CarRacing域中的100个部署中的每一个都做到这一点。赫布网络更通用,但特定任务/机器人形态的性能可能更低,这不足为奇:学习通常会花费时间,但会导致更大的泛化[61]。
有趣的是,随机初始化的网络最近在不同的域中显示出特别有趣的特性[16-18]。我们通过证明随机权重是快速适应某些复杂RL域所需要的,从而为这一最新趋势增添了新趋势,因为它们已与表达神经可塑性机制配对。
未来一个有趣的工作方向是用神经调节可塑性扩展该方法,该方法已被证明可以改进正在进化的可塑性神经网络[62]和通过反向传播训练的可塑性网络[63]的性能。除其他特性外,神经调节还允许某些神经元调节神经网络中连接的可塑性水平。此外,复杂的神经调节系统在动物大脑中对于更精细的学习形式似乎至关重要[64]。当给网络一个额外的奖励信号作为基于目标的适应的输入时,这种能力尤其重要。这里介绍的方法开拓了其他有趣的研究领域,例如进化智能体神经结构[65]或通过更间接的基因型到表型映射[66, 38]编码学习规则。
在神经科学界,关于动物行为的哪些部分属于天生,通过学习获得哪些部分的问题引起了激烈的争论[38]。有趣的是,这些生物网络的连通性中的随机性可能比以前认识到的更为重要。例如,随机反馈连接可以使生物大脑执行某种反向传播[67],并且最近有证据表明前额叶皮层实际上可以结合使用随机连接和赫布学习[19]。据我们所知,这是第一次将随机网络和赫布学习相结合应用于复杂的RL问题,我们希望该方法可以激发未来神经科学和机器学习之间思想的进一步交叉[20]。
与当前试图尽可能通用的RL算法相反,动物神经系统偏向于进化,使其能够通过将其学习限制在对其生存至关重要的方面来快速学习[38]。本文提出的结果(其中先天的智能体的知识是进化的学习规则)朝这个方向迈出了一步。我们所提出的方法打开了有趣的未来研究方向,并提出不要强调网络权重所扮演的角色,而应将重点更多地放在学习规则本身上。关于两个复杂且不同的RL任务的结果表明,这种方法值得进一步探索。
6 Appendix
6.1 Network Weight Visualizations
图6显示了一个示例,说明了如何在特定时间步骤上可视化网络的权重。每个像素代表每个突触连接的权重值wij。我们分别表示三个全连接层(FC1层,FC2层,FC3层)的权重:四足网络的输入空间为28,三个全连接层为[128, 64, 8]个神经元,因此FC1层上方的矩形的水平尺寸为28,垂直尺寸为128,FC2层的水平尺寸为64,垂直尺寸为128,最后一层的FC3层垂直方向的尺寸为64,水平方向的尺寸为8,这对应于动作空间的尺寸。较暗的像素表示负值,而白色像素是正值。在CarRacing环境中,权重被标准化为间隔[-1, +1],而四足动物则具有无限的权重。

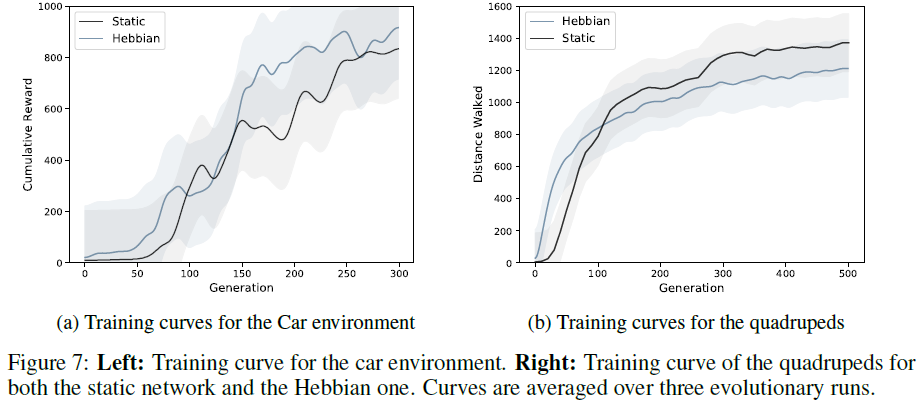
6.2 Training efficiency
我们在图7中显示了针对这两种方法和两种域的历代训练。即使赫布方法必须优化大量参数,两种方法的训练性能也同样快速提高。
6.3 Hebbian rules
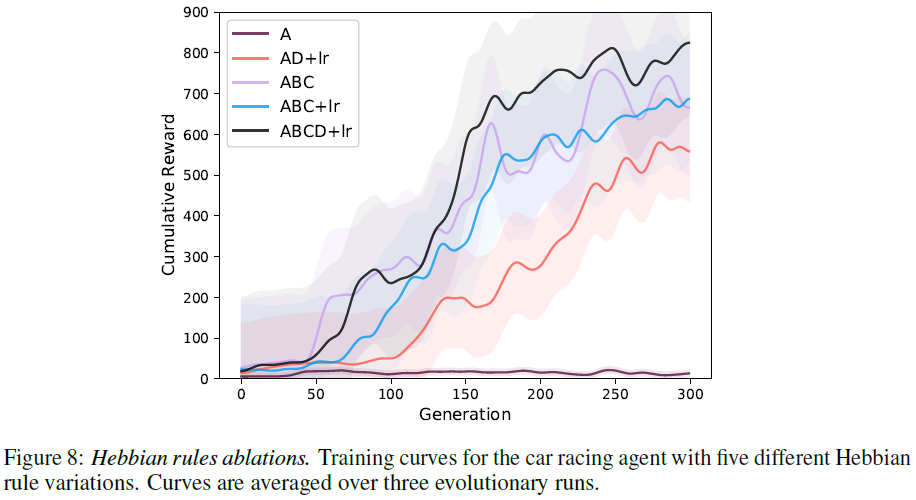
我们分析了在赛车环境中从等式2派生的赫布规则的不同风格。对于本实验,我们不进化卷积层的参数,而是在初始化时将它们随机固定;我们只进化控制前馈层的赫布系数。从最简单的A系数都为零开始,到最普遍的形式,所有四个A, B, C, D系数和生涯内学习率η都存在(图8):
![]()
静态的和所有广义的赫布模型都可以解决基于像素的任务,只有每个突触A具有唯一系数的赫布版本无法解决该任务。具有更大系数的赫布模型收敛速度较慢,这可以通过以下事实来解释:较大的参数空间需要更多代才能通过ES算法进行探索。
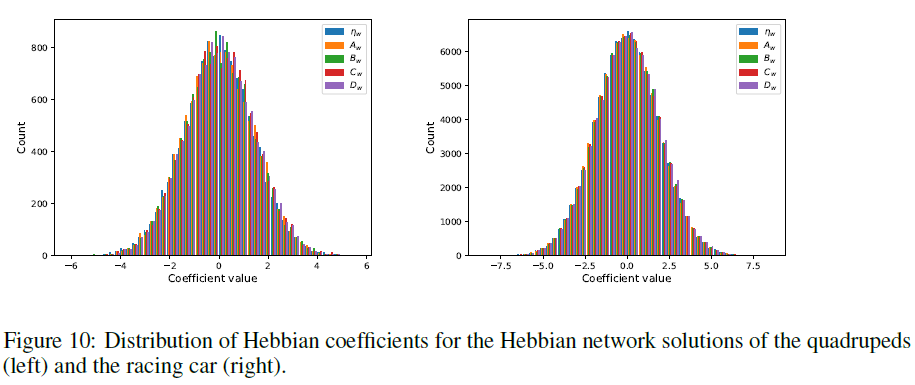
我们还显示了最通用的ABCD+η版本的系数分布(图10),这显示了正态分布。我们假设这种分布对于使权重的自组织不增长到极值可能是必需的。分析最终的权重分布和进化规则,为许多有趣的未来研究方向开辟了道路。
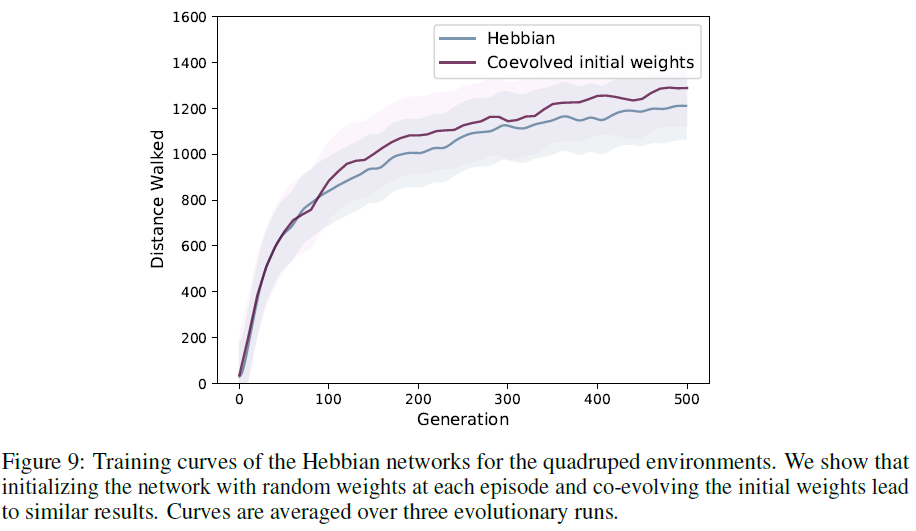
6.4 Evolving initial weights and learning rules
我们进行了实验,除了赫布系数外,还对网络的初始权重进行进化,而不是在每个回合时都对其进行随机初始化。为此,我们对正常噪声进行了两次采样([44]中的算法2,步骤5),然后计算所得解决方案对的适应度(赫布系数,初始权重)。令人惊讶的是,这并没有增加智能体的训练效率(图9)。此外,我们发现,在我们共同进化的初始条件下的CarRacing环境中,运行更有可能因局部最优而停滞:3个运行中有2个发现具有良好性能的网络(至少800个奖励),而第三个由于性能低下而停顿(奖励少于100)。这一发现可以用共同进化在ES算法中引入的额外困难以及初始权重和赫布系数的额外彩票初始化来解释[68]。但是,该系统的其他可能实现方式可能会产生更好的结果,并且在较小的网络中进化连接的赫布系数和学习规则都显示出了希望[45, 13, 66]。