强化学习第2版第3章笔记——有限马尔可夫决策过程

　　在这一章中，我们将正式介绍有限马尔可夫决策过程(有限MDP)，这也是本书后面要试图解决的问题。这个问题既涉及"评估反馈"(如前面介绍的赌博机问题)，又涉及"发散联想"，即在不同情境下选择不同的动作。MDP是序列决策的经典形式化表达，其动作不仅影响当前的即时收益，还影响后续的情况(又称状态)以及未来的收益。因此，MDP涉及了延迟收益，由此也就有了在当前收益和延迟收益之间权衡的需求。

　　MDP是强化学习问题在数学上的理想化形式，因为在这个框架下我们可以进行精确的理论说明。

 

3.1　　"智能体-环境"交互接口

　　MDP就是一种通过交互式学习来实现目标的理论框架。进行学习及实施决策的机器被称为智能体(agent)。智能体之外所有与其相互作用的事物都被称为环境(environment)。这些事物之间持续进行交互，智能体选择动作，环境对这些动作做出相应的响应，并向智能体呈现出新的状态。环境也会产生一个收益，通常是特定的数值，这就是智能体在动作选择过程中想要最大化的目标。

　　更具体地说，在每个离散时刻t = 0, 1, 2, 3, ...，智能体和环境都发生了交互。¹ 在每个时刻 t，智能体观察到所在的环境状态的某种特征表达，S_t ∈ S，并且在此基础上选择一个动作，A_t ∈ A(s)。² 下一时刻，作为其动作的结果，智能体接收到一个数值化的收益，，并进入一个新的状态S_t+1。³ 从而，MDP和智能体共同给出了一个序列或轨迹，类似这样：

S₀, A₀, R₁, S₁, A₁, R₂, S₂, A₂, R₃, ...

　　在有限MDP中，状态、动作和收益的集合(S、A和R)都只有有限个元素。在这种情况下，随机变量R_t和S_t具有定义明确的离散概率分布，并且只依赖于前继状态和动作。也就是说，给定前继状态和动作的值时，这些随机变量的特定值，s' ∈ S和r ∈ R，在 t 时刻出现的概率是：

对于任意s', s ∈ S, r ∈ R, 以及a ∈ A(s)。函数p定义了MDP的动态特性。

　　在马尔可夫决策过程中，由p给出的概率完全刻画了环境的动态特性。也就是说，S_t和R_t的每个可能的值出现的概率只取决于前一个状态S_t-1和前一个动作A_t-1，并且与更早之前的状态和动作完全无关。这个限制并不是针对决策过程，而是针对状态的。状态必须包括过去智能体和环境交互的方方面面的信息，这些信息会对未来产生一定影响。这样，状态就被认为具有马尔可夫性。我们假设这种马尔可夫性贯穿本书，尽管从第II部分开始，我们会考虑不依赖这种性质的近似方法，并且在第17章中考虑如何从非马尔可夫观测中学习并构造马尔科夫状态。

　　MDP框架非常抽象与灵活，并且能够以许多不同的方式应用到众多问题中。一般来说，动作可以是任何我们想要做的决策，而状态则可以是任何对决策有所帮助的事情。

　　特别地，智能体和环境之间的界限通常与机器人或动物身体的物理边界不同。一般情况下，这个界限离智能体更近。例如，机器人的发动机、机械连接及其传感硬件通常应被视为环境的一部分，而非智能体的一部分。同样，如果我们将MDP框架应用到人或动物身上，肌肉、骨骼和感觉器官也应被视为环境的一部分。类似地，收益发生在自然或人工学习系统的物理结构之内，但却算在智能体之外。

　　我们遵循的一般规则是，智能体不能改变的事物都被认为是在外部的，即是环境的一部分。但我们并不是假定智能体对环境一无所知。例如，智能体通常会知道如何通过一个动作和状态的函数来计算所得到的收益。但是，我们通常认为收益的计算在智能体的外部，因为它定义了智能体所面临的任务，因此智能体必然无法随意改变它。事实上，在某些情况下，智能体可能了解环境的一切工作机制，然而即便如此，它面临的强化学习任务仍然是困难的，正如我们知道魔方的原理，却仍然无法解决它。智能体和环境的界限划分仅仅决定了智能体进行绝对控制的边界，而并不是其知识的边界。

　　出于不同的目的，智能体-环境的界限可以被放在不同的位置。在一个复杂的机器人里，多个智能体可能会同时工作，但它们各自有各自的界限。在实践中，一旦选择了特定的状态、动作和收益，智能体-环境的界限就已经被确定了，从而定义了一个特定决策任务。

　　MDP框架是目标导向的交互式学习问题的一个高度抽象。任何目标导向的行为的学习问题都可以概括为智能体及其环境之间来回传递的三个信号：一个信号用来表示智能体做出的选择(行动)，一个信号用来表示做出该选择的基础(状态)，还有一个信号用来定义智能体的目标(收益)。这个框架也许不能有效地表示所有决策学习问题，但它已被证明其普遍适用性和有效性。

 

1 为了简化问题，我们只关注离散时间，尽管有许多方法都拓展到了连续时间的情况(例如，Bertsekas和Tsitsiklis, 1996; Doya, 1996)。

2 为了简化符号，我们有时假设一个特殊情况，即所有状态的动作集合都是一样的，便可简单记为A。

3 我们用R_t+1而不是R_t来表示A_t导致的收益，因其强调下一时刻的收益和下一时刻的状态是被环境一起决定的。很不幸的是，这两种表示方法都在文献中广泛使用，在阅读的时候需要特别注意。

 

3.2　　目标和收益

　　在强化学习中，智能体的目标被形式化表征为一种特殊信号，称为收益，它通过环境传递给智能体。非正式地说，智能体的目标是最大化其收到的总收益。我们可以将这种非正式想法清楚地表述为收益假设：

我们所有的"目标"或"目的"都可以归结为：最大化智能体接收到的标量信号(称之为收益)累积和的概率期望值。

使用收益信号来形式化目标是强化学习最显著的特征之一。

　　智能体总是学习如何最大化收益。如果我们想要它为我们做某件事，我们提供收益的方式必须要使得智能体在最大化收益的同时也实现我们的目标。因此，至关重要的一点就是，我们设立收益的方式要能真正表明我们的目标。特别地，收益信号并不是传授智能体如何实现目标的先验知识。¹ 收益信号只能用来传达什么是你想要实现的目标，而不是如何实现这个目标。²

 

1 要传授这种先验知识，更好的办法是设置初始的策略，或初始价值函数，或对这两者施加影响。

2 17.4节对有效收益信号的设计做了进一步的探讨。

 

3.3　　回报和分幕

　　一般来说，我们寻求的是最大化期望回报，记为G_t，它被定义为收益序列的一些特定函数。在最简单的情况下，回报是收益的总和：

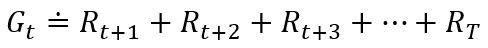
其中T是最终时刻。这种方法在有"最终时刻"这种概念的应用中是有意义的。在这类应用中，智能体和环境的交互能被自然地分成一系列子序列(每个序列都存在最终时刻)，我们称每个子序列为幕³ (episodes)，例如一盘游戏、一次走迷宫的旅程或任何这类重复性的交互过程。每幕都以一种特殊状态结束，称之为终结状态。随后会重新从某个标准的起始状态或起始状态的分布中的某个状态样本开始。

　　另一方面，在许多情况下，智能体-环境交互不一定能被自然地分为单独的幕，而是持续不断地发生。我们称这些为持续性任务。

　　为了避免最大化的回报趋于无穷，我们需要引入一个额外概念，即折扣。根据这种方法，智能体尝试选择动作，使得它在未来收到的经过折扣系数加权后的(我们称为"折后")收益总和是最大化的。特别地，它选择A_t来最大化期望折后回报：

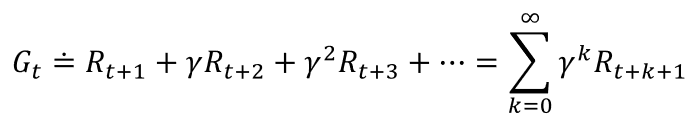
其中，γ是一个参数，0 < γ < 1，被称为折扣率。

 

3.4　　分幕式和持续性任务的统一表示法

　　我们可以把回报表示为：

 

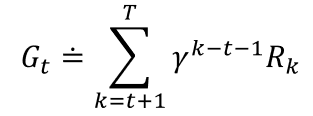
3.5　　策略和价值函数

 

3.6　　最优策略和最优价值函数

 

3.7　　最优性和近似算法

 

3.8　　本章小结