Event-driven Random Backpropagation: Enabling Neuromorphic Deep Learning Machines

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

Frontiers in neuroscience, (2017)

 

Abstract

　　神经形态计算中的一项持续挑战是设计出与大脑的时空约束兼容的通用且计算效率高的推断和学习模型。梯度下降反向传播规则是深度学习中无处不在的强大算法，但是它依赖于存储有高精度内存的网络范围信息的即时可用性。但是，最近的工作表明，确切的反向传播权重对于学习深度表征并不重要。随机反向传播将反馈权重替换为随机权重，并鼓励网络调整其前馈权重，以学习(随机)反馈权重的伪逆。在此，我们演示了一个事件驱动的随机反向传播(eRBP)规则，该规则使用误差调节的突触可塑性来学习神经形态计算硬件中的深度表征。该规则非常适合在神经形态硬件中使用两室LIF神经元以及膜电压调节且脉冲驱动的可塑性规则来实现。我们的结果表明，使用eRBP可以在不使用反向传播梯度的情况下快速学习深度表征，与在GPU上进行ANN仿真相比，实现了几乎相同的分类精度，同时对学习过程中的神经和突触状态量化具有鲁棒性。

 

I. INTRODUCTION

　　生物神经元和突触可以为推断和学习机器提供蓝图，这些机器比主流计算机的能源效率可能高出数千倍。但是，当今神经形态硬件的应用范围和规模仍然受到限制，这主要是由于缺乏通用且有效的推断和学习算法，这些算法不符合大脑的时空限制。
　　机器学习和深度学习具有通用，模块化和容错的特性，因此可以很好地利用神经形态硬件解决广泛的应用[1], [2], [3]。一个悬而未决的问题是，深度神经网络中的学习阶段是否也可以在神经形态硬件中有效地进行。在线执行学习可以赋予动态或受较少控制的环境(不存在先前的代表性数据集)连续的适应性，并为认知行为者提供更细粒度的上下文意识，同时减少学习的精力。但是，深度学习通常依赖于存储有高精度内存的网络范围信息的即时可用性。深度学习在类脑基底上的非局限性是由于梯度下降反向传播(BP)规则[4]所致，这需要在反馈路径中转置前馈矩阵。在数字计算机中，对此类信息的访问通过冯·诺依曼瓶颈来进行，这决定了计算基质的基本局限性。沿多个核(例如在GPU中)分布计算是缓解此问题的一种流行解决方案，但即使在那儿，BP的可伸缩性也经常受到其内存密集型操作的限制[5]。

　　在此，我们以梯度BP规则的近似形式的最新进展[6], [7], [8]为基础，用于训练神经形态硬件中使用的脉冲神经元类型，以执行监督学习。这些近似值通过将BP权重替换为随机权重来解决非局部性问题，从而导致基准任务的分类性能损失极小[8], [9]。尽管仍然缺乏对随机BP (RBP)的一般理论理解，但对线性网络的扩展仿真和分析表明，在学习过程中，网络会调整其前馈权重以学习(随机)反馈权重的伪逆的近似值，至少在交流梯度方面同样出色。

　　我们描述了如何将事件驱动的RBP实现紧密地嵌入神经元动态中，并为神经形态深度学习机器奠定基础。我们的结果表明，在线训练的脉冲网络的MNIST分类性能与在数字计算机上运行的等效ANN的性能几乎相同。最后，我们证明了eRBP在固定宽度仿真中具有鲁棒性，并且具有有限的神经和突触状态精度。

 

II. EVENT-DRIVEN RANDOM BACKPROPAGATION

　　事件驱动的RBP (eRBP)是由突触后神经元膜电压控制且自上而下的误差调节的突触前脉冲驱动规则。这个额外的调节因子背后的想法在本质上与以前的三因素可塑性规则的生物学合理的模型[10]相似，并且被认为可以支持监督，无监督和强化学习，这一想法也在[8]中得到了报道。eRBP学习规则可以总结如下：

其中S^pre(t)是突触前脉冲序列，而Θ是在突触后膜电位V[t]上评估的突触神经元激活函数的导数。对于最终输出(预测)层，与增量规则类似，T等于分类误差E。对于隐含层，T等于误差乘以随机向量G_i，即。在学习期间，所有G_ij都是固定的。

　　对于IF神经元，我们发现boxcar函数代替Θ可提供很好的结果，同时比计算激活函数的精确导数更适合于硬件实现。这种选择的动机是，具有绝对不应期的LIF神经元的激活函数可以通过饱和的阈值单元近似。使用具有边界V_min和V_max的boxcar函数，eRBP更新仅包括加法和比较，并且可以使用以下操作为每个神经元捕获：

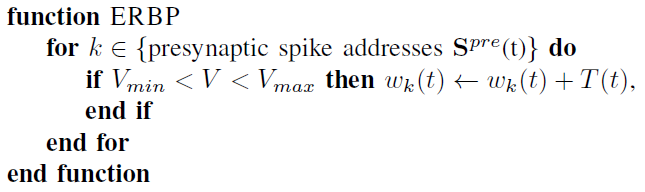
该规则使人想起基于膜电压的规则，其中仅当膜电压在资格窗口之内时才诱发脉冲驱动可塑性[11], [12]。此外，ERBP不需要STDP的"因果"更新，因此不需要反向查找表或最近研究的STDP近似形式[13]。该学习规则假定在突触前突触处可获得T(t)调节。在以下部分中，我们将说明如何在IF神经元的神经网络中实现eRBP。

 

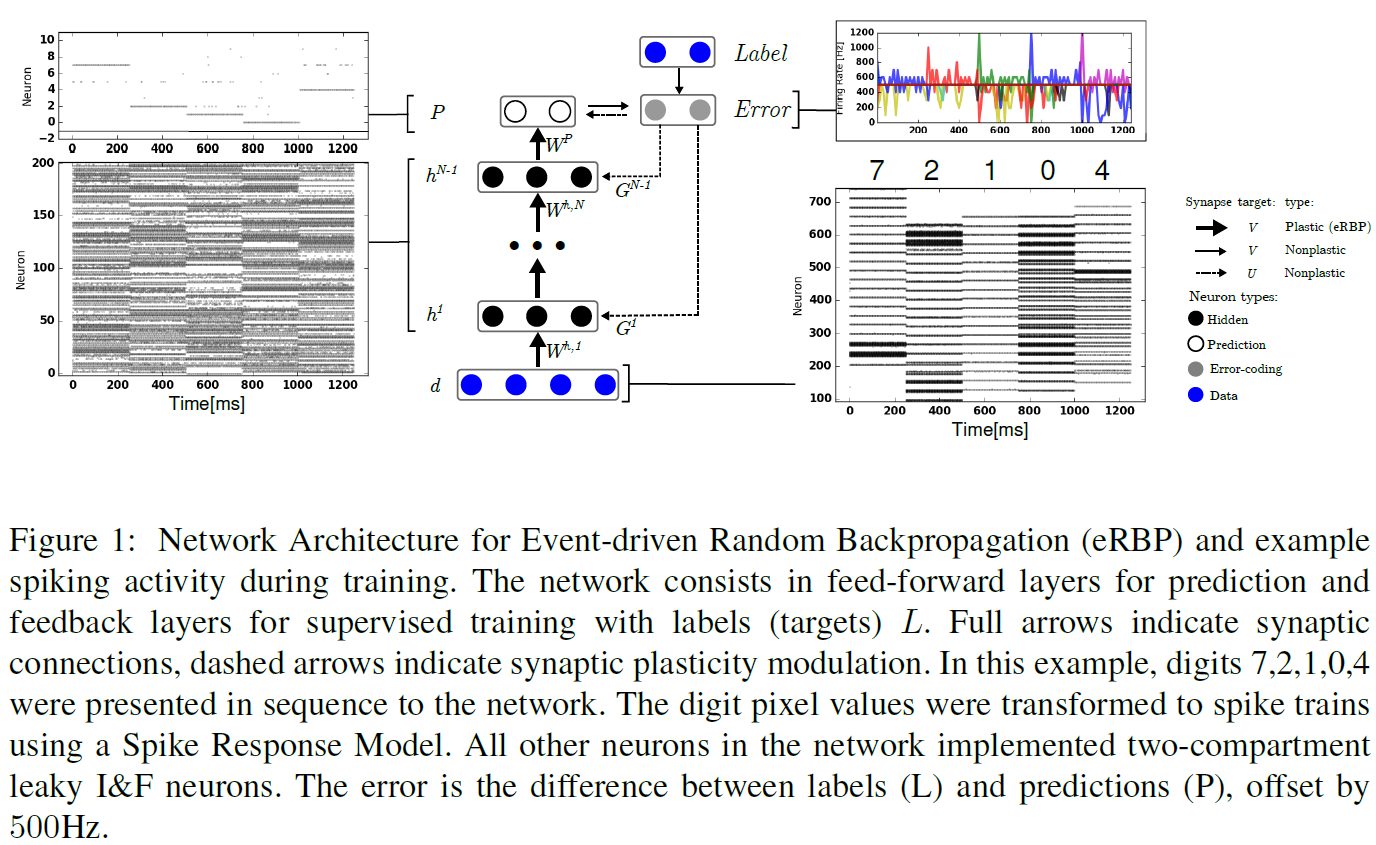
A. A Spiking Network for eRBP with Error-Coding Neurons

　　用于eRBP的网络由一个或两个前馈层组成(图1)，尽管结果可以推广到任意数量层之间的任何前馈连接。标记为P的顶层是预测。来自误差群体的反馈将直接反馈到隐含层的神经元。这种类型的反馈也称为"skipped RBP"[9]。这种直接反馈简化了将误差调节传递到隐含神经元的过程，并提高了在标准基准测试中的学习性能[9]。

　　所提出的网络由三种类型的神经元组成：

1）误差编码神经元是遵循线性动态的non-leaky IF神经元：

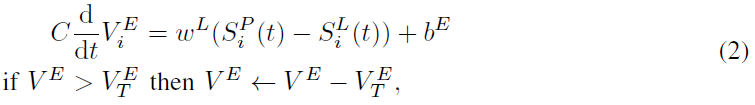
其中和分别是来自预测神经元和标记(教学信号)的脉冲序列，b^E是固定的公共偏差。V和U的时序依赖性的表示法被省略以减少混乱。误差编码神经元的发放率与输入的线性整流成比例。当预测神经元正确分类时，rhs上的两个项将抵消，并且神经元以恒定发放率发放。当误差发生时，发放率从线性下降到整流点。 

2）隐含神经元遵循基于电流的LIF动态：

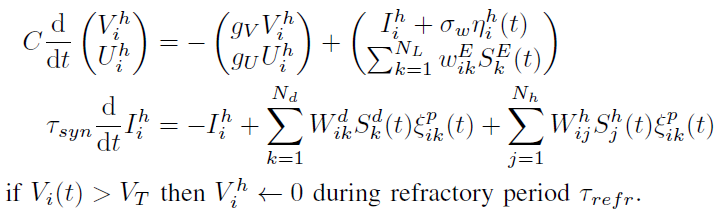
其中和分别为数据神经元和隐含神经元的脉冲序列，I^h为基于电流的突触动态，而为发放率为100Hz的泊松过程，以及ξ^p为概率为p的随机伯努利过程。先前已证明后一种类型的随机性有利于脉冲序列的正则化和去相关，同时易于在神经形态硬件中实现[2]。在这项工作中，我们考虑前馈网络，即权重矩阵W^h被限制为上对角线。每个神经元都配有一个独立的"树突"区室，其遵循与膜电位相似的亚阈值动态，其中S^E(t)是误差编码神经元的脉冲序列，W^E是固定的随机矩阵，因此对于每个隐含神经元 i，。此条件确保了误差编码神经元的自发发放率不会使学习产生偏差。突触权重动态遵循树突状调节和神经状态门控规则：

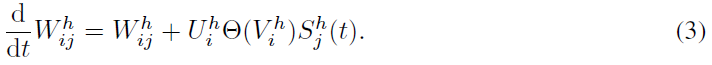
3）预测神经元，除了树突区室，突触和突触权重更新遵循与隐含神经元相同的动态：

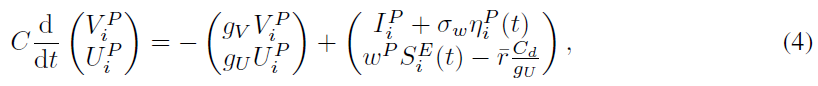
其中额外的偏差项抵消了误差编码神经元的自发发放率的影响。

 

B. Experimental Setup and Software Simulations

　　我们在MNIST手写数字数据集上训练了全连接的前馈网络，数据集分为三组，分别用于训练，验证和测试(分别为50000, 10000, 10000个样本)。在一个训练epoch中，每个训练数字均在250ms内依次显示。使用"sigmoid神经元"将样本的像素强度在线转换为脉冲序列，即具有指数激活(hazard)函数且不应期与隐含和预测神经元相匹配的脉冲响应模型(SRM)[14]。我们使用两种配置对eRBP进行了测试：一种具有加性噪声(σ_w > 0, p = 1, 标记为eRBP)，一种具有乘性噪声，实现为连接上的消隐噪声(消隐概率p < 1且σ_w = 0，标记为peRBP)。随机性有助于减少隐含层和预测层之间的同步。此外，为防止网络学习到数字之间的(虚假)转换，突触权重在每个数字表示的前50ms窗口中均未更新。

　　我们在两种不同的实现方式上测试了eRBP训练：1）基于Auryn仿真器[15]的SNN，以及2）具有量化神经状态和权重的硬件兼容仿真器。使用等效的非脉冲神经网络，将结果与Theano [16]中执行的RBP和标准BP的GPU实现进行比较。我们专注于置换不变(PI)任务，以强调网络是非结构化的(例如无卷积或池化)。

 

III. RESULTS

A. Spiking Networks with eRBP Learn with High Accuracy

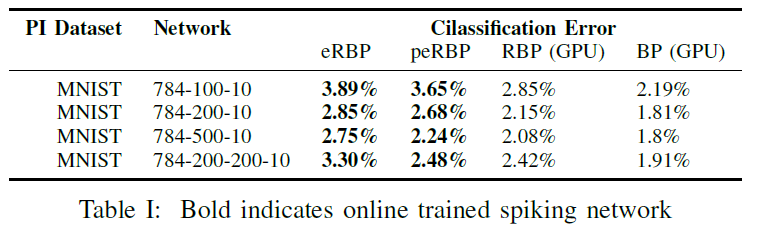
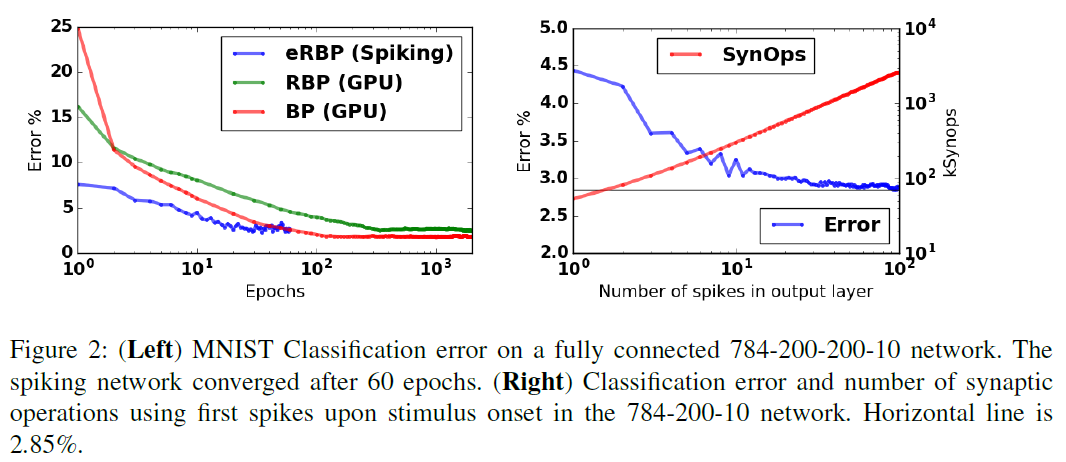
　　尽管eRBP也可以推广到更深层的网络，但我们在由一两个隐含层组成的网络中测试了eRBP(表I)。我们没有对绝对分类性能进行优化，而是将其与经过RBP和标准BP训练的等效ANN进行比较，并对其自由参数进行了微调以实现分类任务的高精度。在大多数网络配置中，eRBP达到的性能与在人工网络中使用RBP达到的性能相当。配备概率连接的ERBP (peRBP)总体上表现更好，而对于更深的784-200-200-10网络，则表现更好。这是因为随着学习进行，由于较大的突触权重(并因此是突触前输入)，很大一部分神经元趋向于以其最大发放率发放并使其跨层的脉冲活动同步。eRBP公式固有地假设简单的发放率模型无法很好地捕获同步的脉冲活动。但是，随机消除突触前脉冲的概率连接有效地在突触前脉冲序列中引入了不规则性，从而改进了学习效果。另一方面，当突触前​​输入的幅度较大时，加性噪声的影响相对较小。总体而言，所学习的分类精度与使用精确的标准反向传播[17]的离线训练SNN(例如GPU)所获得的分类精度相当。

B. Classification with Single Spikes

　　刺激发作后784-200-10网络的响应约为一个突触时间常数。从刺激开始到τ_s = 4ms之后使用初次脉冲进行分类，导致误差小于4.5％(图2)，并且随着输出层脉冲数目的增加而稳定地提高。使用初次脉冲进行分类会产生53407个突触操作(平均超过10000个测试样本)，这可能会导致在专用神经形态硬件中每个分类产生亚微焦耳能量[18]。低等待时间和准确响应似乎与网络计算背后的固有发放率代码不一致。但是，基于初次脉冲时间的代码与发放率代码一致，因为预计发放率高的神经元会先发放[14]。另外，刺激的发作引起同步活动的爆发，这进一步有利于响应的迅速发作。这些结果表明，尽管具有潜在的发放率代码，但eRBP仍可利用脉冲动态特性，与专门针对单脉冲分类训练的脉冲网络相比[19]。

C. Spiking Networks Equipped with ERBP Learn Rapidly

　　与运行RBP的ANN相比，SNN eRBP需要更少的时间来达到分类性能峰值。使用小批量数据样本(n_batch = 100)训练ANN。借助矢量化库或利用GPU，迷你批处理可提高传统硬件中的学习速度，并导致更平滑的收敛。但是，权重更新是在小批量上平均的，因此与每个epoch的脉冲网络(其中n_batch有效等价于一个可以使用n_batch = 1来训练的标准ANN)相比，每个epoch的权重更新要少n_batch倍，但是在标准平台上学习变得很慢，因为无法跨数据样本对这些操作进行矢量化处理。鉴于神经形态硬件的潜在应用通常涉及实时流数据，因此对脉冲网络的这种更快的学习是在线梯度下降的幸运副产物。

D. Learning with Low Precision, Fixed Point Representations

　　当使用定点表示的突触权重的精度小于16位时，随机梯度下降的有效性会降低[20]。这是因为量化确定了最小的学习率并限制了突触权重的范围，从而防止了对数据集迭代之间的可变性求平均。由于空间限制和内存泄漏，在神经形态芯片设计中追求的内存与计算电路的紧密集成具有挑战性。因此，由于神经状态和参数以及突触权重的量化，脉冲网络的全精度(甚至16位)计算机仿真可能无法代表在专用神经形态芯片中可以获得的性能。
　　扩展的仿真表明，在10位精度下的随机BP性能与未量化的权重是无法区分的[9]，但是尚未测试不使用minibatches的在线学习的情况。 在这里，我们假设8位突触​​权重是学习能力和硬件占用空间之间的良好折衷。为了证明对这些约束的鲁棒性，我们使用低精度的定点表示(每个突触权重8位，对于神经状态16位)仿真eRBP网络的量化版本。与现有发现一致，我们在量化的784-100-10网络中对eRBP的仿真表明，在这些条件下eRBP仍然表现良好(图3)。尽管许多权重在边界处聚集，但大多数权重仍留在边界之间。

 

IV. CONCLUSION

　　我们的结果表明，在ANN熟练程度的神经形态平台上使用流脉冲事件数据进行通用深度学习是可以实现的。ERBP可以以非常紧凑的方式实现，同时使用在神经元到神经元的基础上由全局误差调节的局部突触可塑性规则。尽管我们的实验针对的是数字神经形态实现，但是在混合信号神经形态硬件中实现的基于膜电压的学习规则[12]与eRBP兼容，前提是可以通过外部信号在神经元到神经元的基础上调节突触权重更新。因此，神经形态工程学和与eRBP结合的纳米技术的最新进展可能成为空间和功率受限平台中超低功率处理的关键。
　　结合深度学习和RNN的发展，我们预想，这种RBP技术将使模式识别，注意力，工作记忆和动作选择机制的嵌入式学习成为可能，从而为嵌入式计算带来了变革性的硬件架构。