S4NN: temporal backpropagation for spiking neural networks with one spike per neuron
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

International Journal of Neural Systems, Vol. 30, No. 6 (2020) 2050027
Abstract
我们为多层SNN提出了一种新的监督学习规则,该规则使用一种称为rank-order编码的时序编码形式。使用这种编码方案,所有神经元对每个刺激发放一个脉冲,但发放序列携带信息。特别是在读出层中,第一个发放的神经元决定刺激的类别。我们为这种网络推导了一种新的学习规则,称为S4NN,类似于传统的误差反向传播(但基于延迟)。我们展示了如何在具有任意层数的前馈网络中反向计算近似误差梯度。这种方法通过监督的多全连接层SNN达到了最先进的性能:MNIST数据集的测试精度为97.4%,Caltech Face/Motorbike数据集的测试精度为99.2%。但是,我们使用的神经元模型(non-leaky IF)比以前所有工作中使用的模型都简单得多。S4NN的源代码可在https://github.com/SRKH/S4NN中公开获得。
1 Introduction
生物神经元通过称为"脉冲"或"动作电位"的短模式电脉冲进行交流。每个神经元都整合突触前神经元的传入脉冲,并且每当其膜电位达到某个阈值时,它还会将传出脉冲发送到下游神经元。在大脑中,除了脉冲发放率外,脉冲时间在神经元处理信息的过程中也起着重要作用[1, 2]。因此,SNN比ANN更具有生物学合理性[3, 4, 5, 6],并且由于SNN使用以大规模并行方式处理的稀疏异步二值信号,因此它们是目前研究大脑如何在神经元描述级别进行计算的最优选择之一。但是,SNN也吸引了AI技术,尤其是边缘计算,因为它们在所谓的神经形态芯片上的实现比在ANN上实现的(通常在GPU或类似硬件上实现)耗费的能源要少得多,主要是因为它们可以利用基于事件的高效计算[4, 7, 8, 9, 10, 11, 12]。
最近,许多研究人员为开发用于SNN的直接监督学习算法进行了广泛的研究[7]。对此的主要挑战是脉冲神经元在发放时间的阈值激活函数的不可微分性。解决此问题的一种方法是考虑脉冲发放率,而不是确切的脉冲时间[13, 14, 15]。第二种方法是使用随时间变化的平滑脉冲函数[16]。第三组方法在脉冲时间[8, 17, 18, 19, 20, 21, 22]使用替代梯度。最后一种方法称为延迟学习,是本文的重点。在这种方法中,神经元的发放时间取决于其膜电位或突触前神经元的发放时间[23, 24, 25]。这样,不再需要推导阈值激活函数。
更具体地说,我们的目标是使用SNN对静态输入(例如,图像)进行分类,在该SNN中,每个神经元最多发放一次,但最活跃的神经元最先发放[26, 27, 28, 29, 30, 31, 24, 32, 33, 25, 34, 35, 36]。因此,脉冲延迟或发放序列会携带信息。在此,我们在提出的SNN的所有层中都使用了简单的non-leaky IF神经元[37]。实际上,每个神经元都简单地整合经过时间加权的输入脉冲(从瞬时突触接收),没有泄漏,并且在第一次超过其阈值后立即发出一个脉冲,如果从未达到此阈值,则仅发出零脉冲。在读出层中,每个类别有一个神经元。一旦这些神经元之一发放,网络就会为输入分配相应的类别,并且只有少数神经元发放时,计算才能停止。因此,这种编码方案在脉冲数量上非常经济。
在这项工作中,我们将最初为ANN设计的众所周知的反向传播算法[38]应用于这种SNN。反向传播已被证明可以解决多层神经网络中极其困难的分类问题,从而导致了所谓的"深度学习"革命[39]。反向传播的目的是解决多层信度分配问题[40]。也就是说,发现隐含层应该采取什么措施以最小化读出层的损失,这促使我们和其他工作[23, 24, 25, 34]通过以下方式使反向传播适应单脉冲SNN。我们使用上述方法的主要优势是使用了一种更为简单的神经元模型:具有瞬时突触的non-leaky IF神经元。但它在MNIST数据集上达到了相当的精度[41]。

2 Methods
所提出的单脉冲监督SNN (S4NN)包括一个输入层,将输入数据转换为脉冲序列并将其馈送到网络中,然后是一个或多个处理输入脉冲的non-leaky IF隐含层,最后是non-leaky IF神经元输出层(每个类别一个神经元)。图1演示了具有两个隐含层的S4NN。在此,我们在输入层中使用一种被称为time-to-first-spike的时序(即rank-order)编码,它非常稀疏,每个输入值最多产生一个脉冲。随后的神经元也仅限于精确发放一次。
为了训练网络,使用了反向传播算法的时序版本。我们假设一个图像分类任务,每个类别有多个图像。首先,通过考虑第一个输出神经元来做出关于输入图像类别的网络决策。然后,通过将每个输出神经元的实际发放时间与目标发放时间进行比较,计算出每个神经元的误差(请参见2.5小节)。最后,这些误差会通过各层反向传播,权重会通过随机梯度下降得到更新。同时,时序反向传播面临两个挑战:定义目标发放时间和计算神经元发放时间相对于其膜电位的导数。为了克服这些挑战,所提出的学习算法使用相对目标发放时间和近似导数。
2.1 Time-to-first-spike coding
SNN的第一步是将模拟输入信号转换为代表相同信息的脉冲序列。后续神经元中的神经处理应与此编码方案兼容,以便能够解密输入脉冲中编码的信息。在此,我们对进入层(其中较大的输入值对应于较早的脉冲)使用time-to-first-spike编码,并在后续层中的IF神经元发放一次。
考虑像素范围在[0, Imax]内的灰度图像,每个输入神经元在范围[0, tmax]的单个脉冲时间内对相应的像素值进行编码。第 i 个输入神经元的发放时间ti是根据第 i 个像素强度值Ii计算的,如下所示:

因此,将输入层(层0)中第 i 个神经元的脉冲序列定义为:
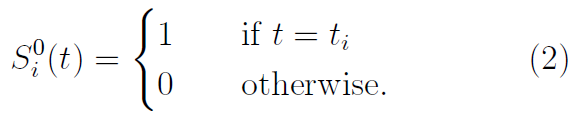
值得注意的是,这种简单的强度到延迟代码不需要任何预处理步骤,例如应用SNN中常用的Gabor或DoG滤波器,特别是在那些具有STDP学习规则且无法处理均质表面的应用中[30, 31, 42]。而且,它对每个像素仅产生一个脉冲,因此所获得的脉冲序列比发放率编码中常见的稀疏。
后续层的神经元一旦达到阈值,就会发放,输出层中的第一个发放的神经元将决定网络决策。因此,网络决策取决于整个网络的最早脉冲。换句话说,所有层中的神经信息都以最早的神经元的脉冲时间编码。因此,可以说,time-to-first-spike信息编码也在后续层中起作用。
2.2 Forward path
S4NN由多层non-leaky IF神经元组成,层数没有限制,因此,S4NN可以实现任意数量的隐含层。在时间点 t 的第 l 层中的第 j 个神经元的膜电位![]() 计算为:
计算为:
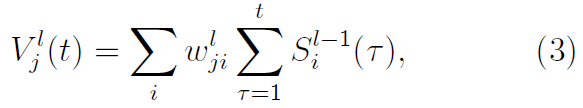
其中![]() 和
和![]() 分别是从上一层的第 i 个突触前神经元到神经元 j 的输入脉冲序列和输入突触权重。IF神经元在其膜电位第一次达到阈值
分别是从上一层的第 i 个突触前神经元到神经元 j 的输入脉冲序列和输入突触权重。IF神经元在其膜电位第一次达到阈值![]() 时发出脉冲,
时发出脉冲,

其中,![]() 检查神经元在任何先前的时间步骤是否没有发放。
检查神经元在任何先前的时间步骤是否没有发放。
如上一节所述,输入图像被转换为脉冲序列S0(t),其中每个输入神经元将发出一个延迟范围为[0, tmax],与相应的像素值成反比。这些脉冲朝着网络的第一层传播,每个神经元接收传入的脉冲并更新其膜电位,直到达到其阈值并将脉冲发送到下一层的神经元。对于每个输入图像,仿真都从将所有膜电压重置为零开始,并持续tmax个时间步骤。请注意,在仿真中,任何层的每个神经元最多只能发放一次。在训练阶段,我们需要知道所有神经元的发放时间(参见等式15和等式9),因此,如果神经元是沉默的,我们假设它在最后一个时间步骤tmax处发放一个假脉冲。在测试阶段,神经元可以保持沉默或最多发放一次。最后,关于在我们的网络中部署的time-to-first-spike编码,比其他更早响应的输出神经元确定了输入刺激的类别。
2.3 IF approximating ReLU
在具有ReLU[43]激活函数的传统ANN中,层 l 中索引为 j 的神经元的输出被计算为:

其中![]() 和
和![]() 分别是第 i 个输入和连接权重。因此,具有较大
分别是第 i 个输入和连接权重。因此,具有较大![]() 的ReLU神经元具有较大的输出值
的ReLU神经元具有较大的输出值![]() 。通常,该积分值的主要部分是由于输入量大且连接权重大。在我们的time-to-first-spike编码中,较大的值对应于较早的脉冲,因此,如果IF神经元通过强突触权重接收到这些较早的脉冲,则它也会较早发放。注意,由于网络决策基于输出层中的首次脉冲,因此较早的脉冲会携带更多信息。这样,time-to-first-spike编码就保留在隐含层和输出层中。因此,对于相同的输入和突触权重,我们可以假设ReLU神经元的输出
。通常,该积分值的主要部分是由于输入量大且连接权重大。在我们的time-to-first-spike编码中,较大的值对应于较早的脉冲,因此,如果IF神经元通过强突触权重接收到这些较早的脉冲,则它也会较早发放。注意,由于网络决策基于输出层中的首次脉冲,因此较早的脉冲会携带更多信息。这样,time-to-first-spike编码就保留在隐含层和输出层中。因此,对于相同的输入和突触权重,我们可以假设ReLU神经元的输出![]() 与相应IF神经元的发放时间
与相应IF神经元的发放时间![]() 之间存在等价关系,
之间存在等价关系,

2.4 Backward path
我们假设在具有C个类别的分类任务中,每个输出神经元都分配一个不同的类别。在完成输入模式上的前向路径后,每个输出神经元可能会在不同的时间点出现。如前所述,将输入图像的类别预测为分配给获胜者输出神经元(具有比其他更早发放的输出神经元)的类别。
因此,为了能够训练网络,我们将时序误差函数定义为:
![]()
其中![]() 和
和![]() 分别是第 j 个输出神经元的目标发放时间和实际发放时间。目标发放时间应以正确的神经元比其他神经元更早发放的方式定义。我们使用相对目标发放计算,这在2.5节中有详细说明。在此,我们假设
分别是第 j 个输出神经元的目标发放时间和实际发放时间。目标发放时间应以正确的神经元比其他神经元更早发放的方式定义。我们使用相对目标发放计算,这在2.5节中有详细说明。在此,我们假设![]() 是已知的。
是已知的。
在学习阶段,我们使用随机梯度下降[38](SGD)和反向传播算法来最小化"平方误差"损失函数。对于每个训练样本,损失被定义为:

因此,我们需要针对每个突触权重计算其梯度。为了更新![]() ,即层l - 1的第 i 个神经元和层 l 的第 j 个神经元之间的突触权重,我们有:
,即层l - 1的第 i 个神经元和层 l 的第 j 个神经元之间的突触权重,我们有:

其中η是学习率参数。
让我们定义:

因此,通过考虑等式(8)和等式(12),我们有:
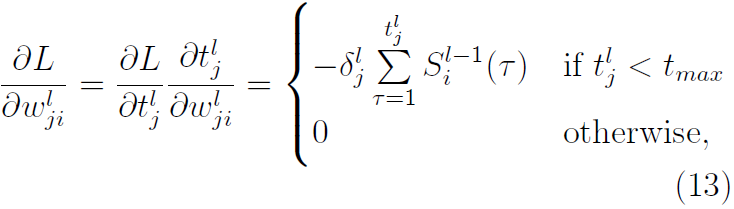
其中对于输出层(即l = o),我们有:

对于隐含层(即l ≠ o),根据反向传播算法,我们有:


为了避免反向传播期间梯度爆炸和消失问题,我们使用归一化梯度。从字面上看,在任何层 l 处,我们在更新权重之前将反向传播的梯度归一化,

为了避免过拟合,我们在等式(10)的"平方误差"损失函数中添加了一个L2-范数正则项![]() (在所有层的所有突触权重上)。参数λ是考虑权重惩罚程度的正则化参数。
(在所有层的所有突触权重上)。参数λ是考虑权重惩罚程度的正则化参数。
2.5 Relative target firing time
由于所提出的网络在时域内工作,因此对于每个输入图像,我们需要定义关于其类别标签的输出神经元的目标发放时间。
一种可能的情况是为每个类别定义一个固定的目标发放时间矢量,以使正确的神经元比其他神经元具有更短的目标发放时间。例如,如果输入图像属于第 i 类,则对于j ≠ i,可以定义![]() 和
和![]() ,其中0 < τ < tmax是获胜者神经元的期望发放时间。通过这种方式,可以鼓励正确的输出神经元在时间τ提前发放,而其他神经元则被迫阻塞发放直到仿真结束。
,其中0 < τ < tmax是获胜者神经元的期望发放时间。通过这种方式,可以鼓励正确的输出神经元在时间τ提前发放,而其他神经元则被迫阻塞发放直到仿真结束。
这种严格的方法有几个缺点。例如,让我们假设一个输入图像属于![]() 的第 i 个类别,这样,正确的神经元就会产生负误差(请参见等式9)。后向路径将更新权重,以使该神经元稍后发放,这意味着网络应该忘记是什么帮助正确的神经元快速发放。这是不可取的,因为我们希望网络尽快做出响应。
的第 i 个类别,这样,正确的神经元就会产生负误差(请参见等式9)。后向路径将更新权重,以使该神经元稍后发放,这意味着网络应该忘记是什么帮助正确的神经元快速发放。这是不可取的,因为我们希望网络尽快做出响应。
另一种情况是使用动态方法来独立确定每个输入图像的目标发放时间。在此,我们提出了一种将实际发放时间考虑在内的相对方法。假设第 i 类的输入图像被馈送到网络,并且获得了输出神经元的发放时间。首先,我们将最小输出发放时间计算为![]() ,然后将第 j 个输出神经元的目标发放时间设置为:
,然后将第 j 个输出神经元的目标发放时间设置为:

其中,γ是一个正常数项,惩罚发放时间接近τ的输出神经元。其他在τ之后很久才发放的神经元也不会受到惩罚,因此,在最小发放时间τ,鼓励正确的输出神经元比其他神经元更早发放。
在特殊情况下,所有输出神经元在仿真过程中均保持沉默,并且其发放时间已手动设置为tmax,我们将目标发放时间计算为:

以鼓励正确的输出神经元在仿真中发放。
2.6 Learning procedure
如前所述,所提出的网络使用SGD的时序版本和反向传播来训练网络。在训练epoch,图像通过time-to-first-spike编码转换为输入脉冲序列(参见第2.1节),然后逐一馈入网络。通过前向路径,任何层的每个IF神经元都会接收传入的脉冲,并在达到阈值时发出脉冲(参见第2.2节)。然后,在计算相对目标输出发放时间(鼓励正确的输出神经元较早发放,参见第2.5节)之后,我们使用时序误差反向传播(参见第2.4节)来更新所有层中的突触权重。请注意,如果神经元在仿真中无法达到阈值,则我们将迫使神经元在最后一个时间步骤发放假脉冲(这对于学习规则是必要的)。在当前输入图像上完成前向和后向处理之后,所有IF神经元的膜电位都将重置为零,并且网络准备好处理下一个输入图像。值得注意的是,在每个输入图像的处理过程中,每个神经元只允许发放一次。
如前所述,除了假脉冲外,IF神经元当且仅当达到阈值时发放。让我们考虑一个IF神经元,其权重降低(在权重更新过程中),使得它无法达到任何训练图像的阈值。现在,它是一个死亡的神经元,只会发出假脉冲。因此,如果神经元死亡,并且在训练epoch中没有发放真脉冲,我们可以通过将其突触权重重置为从与初始权重相同范围内的均匀分布得出的一组新的随机值来重用它。尽管这种情况很少发生,但它可以帮助网络利用其所有学习能力。

3 Results
我们首先使用Caltech 101face/motorbike数据集来更好地演示S4NN中的学习过程及其在大型自然图像上的工作能力。之后,我们在MNIST数据集上评估S4NN,该数据集是SNN领域中广泛使用的基准之一[7],以证明其处理大型多类别问题的能力。表1中提供了用于Caltech face/motorbike和MNIST数据集的S4NN模型的参数设置。




3.1 Caltech face/motorbike dataset
我们在http://www.vision.caltech.edu上可用的Caltech 101 face/motorbike数据集上评估S4NN。图2中提供了一些示例图像。我们在每个类别的200张随机选择的图像上训练网络。此外,我们从每个类别中选择了50张随机图像作为验证集。其余图像用于测试阶段。我们对所有图像进行了灰度处理,并将它们重新缩放为160x250像素。
在第一个实验中,我们使用具有四个IF神经元(隐含层)的全连接结构。输入层具有与输入图像相同的大小(即160x250),并且每个输入神经元的发放时间通过2.1节中解释的首次脉冲时间编码来计算。输出层由与图像类别相对应的两个输出IF神经元(人脸和摩托车神经元)组成。我们将最大仿真时间设置为tmax = 256,并使用从[0, 1]和[0, 50]范围内的均匀分布抽取的随机值初始化输入-隐含和隐含-输出突触权重。我们还将学习率设置为η = 0.1,目标发放时间计算中的惩罚项设置为γ = 3,正则化参数设置为λ = 10-6。所有层中所有神经元的阈值![]() 设置为100。
设置为100。
图3显示了通过训练epoch的训练和验证样本的平均平方和误差(MSSE)的轨迹。MSSE曲线早期的突然跳跃主要是由于第一个训练epoch的巨大权重变化,这可能会使任何输出神经元保持沉默一段时间(仅发出假脉冲),但是,这在下一个epoch正在解决。最后,经过一段epoch后,网络克服这一挑战,并将MSSE降低到0.1以下。
所提出的S4NN在训练样本上可以达到99.75%±0.1%识别精度(即正确分类的样本的百分比),在测试样本上可以达到99.2%±0.2%识别精度,优于该数据集上先前报告的SNN结果(请参见表2)。在Masquelier et al. (2007)[28]中,在此数据集上,由无监督的STDP训练的两层卷积SNN,然后由有监督的基于势能的径向基函数(RBF)分类,达到了99.2%的精度。该网络在第一层使用四个Gabor滤波器和四个标度,并为第二层提取十个不同的滤波器。而且,它不会根据脉冲时间做出决定,而是利用神经元的膜电位进行分类。在Kheradpisheh et al. (2018)[30]中,基于STDP的具有三个卷积层(分别由4, 20和10个滤波器组成)和SVM分类器的SNN可以在该数据集上达到99.1%的精度。该模型还利用最后一层中神经元的膜电位来进行分类。为了进行基于脉冲的分类,Mozafari et al. (2018)[31]的作者提出了一个两层卷积网络,第一层有四个Gabor滤波器,第二层由奖励调节STDP学习了20个滤波器。20个滤波器中的每一个都被分配到一个特定的类别,并由第一个发放的神经元决策。在Caltech face/motorbike数据集上,其精度达到98.2%。该网络的重要特征是通过RL实现了基于脉冲时间的决策。所提出的S4NN还可根据脉冲时间做出决策,仅使用四个隐含神经元和两个输出神经元,就可以达到99.2%的精度。
如第2.2节所述,每个输出神经元都被分配到一个类别,并且基于第一个发放的输出神经元做出网络决策。在学习阶段,关于相对目标发放时间(请参见第2.5节),网络会调整其权重以使正确的输出神经元首先发放(请参见第2.4节)。图4提供了学习阶段开始和结束时人脸和摩托车输出神经元的发放时间(在训练和验证图像上)。如图4A所示,在学习开始时,两个输出神经元的发放时间分布(与图像类别无关)是交错的,这导致机会水平附近的分类精度较差。但是,随着学习阶段的进行和网络学习解决任务,正确的输出神经元往往会更早发放。
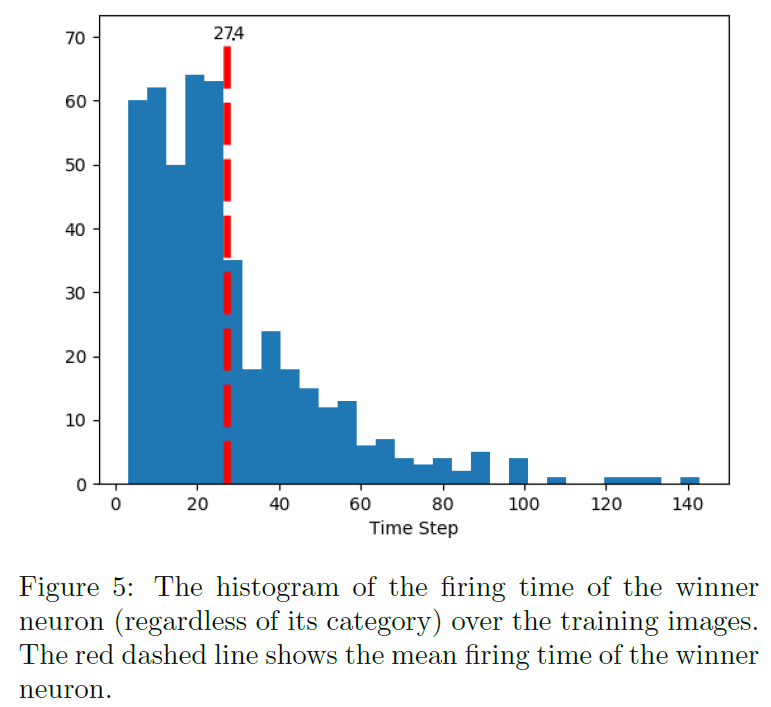
如图4B所示,在学习阶段结束时,对于每个图像类别,其对应的输出神经元在较早的时间步骤处发放,而其他神经元则在很长时间后发放。请注意,在训练阶段,如果神经元在仿真过程中没有发放,我们会在最后一个时间步骤强迫它们发出假脉冲。因此,在测试阶段,我们不需要在输出层中的第一个脉冲发放之后继续仿真。图5示出了获胜者神经元的发放时间的分布。获胜者神经元的平均发放时间为27.4(用红线显示),其中78%的图像中,获胜者神经元在前40个时间步骤中发放。这意味着网络可以非常快速地(相对于最大可能的仿真时间,tmax = 256)做出决定,并且可以准确地做出决定(错误率仅为0.8%)。
由于所使用的网络只有一层全连接神经元的隐含层,因此我们可以简单地通过绘制每个神经元的突触权重来重建其学习模式。图6描绘了学习阶段结束时四个隐含神经元的突触权重。如图所示,神经元#2至#4对各种形状的摩托车具有选择性,从而覆盖了各种形状的摩托车。神经元#1已了解到出现在不同位置的面部组合,因此仅对面部图像做出反应。由于输出神经元之间相互竞争以首先发放,隐含和输出神经元应学习并依赖从输入层(并非全部)接收的早期脉冲。这就是为什么无法从视觉上很好地检测隐含层中学到的特征的原因。图7中绘制了四个隐含神经元中每个神经元的突触权重分布。如图所示,权重的初始均匀分布转换为零均值的正态分布。在此,正权重会鼓励神经元发放其学到的模式,而负权重会阻止神经元为其他模式发放。负权重有助于网络减少不必要的脉冲的机会。例如,从摩托车选择性隐含神经元到面部输出神经元的负突触权重显著减少了面部神经元发生意外脉冲的机会。
此外,我们评估了经过训练的S4NN对抖动噪声的鲁棒性。为此,在测试阶段,我们将从[-J, J]范围内的均匀分布绘制的随机整数添加到输入图像的像素中。我们将抖动参数 J 从0更改为240,步长为20。图8显示了在面部/摩托车数据集上训练的S4NN在受不同抖动水平污染的测试样本上的识别精度。有趣的是,即使对于J = 240,S4NN精度也最多下降5%。它表明,S4NN甚至在强烈的噪声水平下也很鲁棒。实际上,隐含层中的神经元仅对那些参与面部/摩托车分类任务的输入神经元具有强(正或负)突触权重(见图6),而其余大多数输入的突触权重却很小(见图7),并且在神经处理中贡献不大。因此,由于抖动噪声只是改变了脉冲顺序,因此它不会影响IF神经元的行为。请注意,IF神经元是完美的积分器(没有泄漏),并且与泄漏神经元相比,对输入顺序的敏感性较低。
为了评估所提出的时序反向传播算法在更深层次的架构中使用的能力,我们在具有三层网络的Caltech face/motorbike数据集上进行了另一项实验。深度网络由两个隐含层组成,每个隐含层均包含四个IF神经元,然后是具有两个IF神经元的输出层。我们使用从[0, 1], [0, 50], [0, 50]范围内的均匀分布抽取的随机值初始化input-hidden1, hidden1-hidden2和hidden2-output权重。其他参数与上述具有一个隐含层的网络相同。经过25个训练epoch后,该网络在测试图像时达到了99.1%±0.2%的精度,获胜者神经元的平均发放时间为32.1。尽管网络精度平均比较深的网络高0.1%,但该差异在统计上并不显著(每个网络十次不同运行的精度的配对t检验; p值 < 0.05)。


3.2 MNIST Dataset
MNIST[41]是已在SNN文献[7]中广泛使用的基准数据集。我们还在MNIST数据集上评估了所提出的S4NN,该数据集包含60000个训练和10000个测试手写个位数图像。每个图像的大小为28x28像素,并包含数字0-9之一。为此,我们使用了一个S4NN,其中一个隐含层/一个输出层分别包含400和10个IF神经元。输入层的大小与输入图像的大小相同,其中每个输入神经元的发放时间由第2.1节中说明的time-to-first-spike编码决定,最大仿真时间为tmax = 256。隐含输出层的突触权重是从范围为[0, 5]和[0, 50]的均匀分布随机抽取的。将所有层中所有神经元的阈值设置为![]() 。我们将学习率设置为η = 0.2,将目标发放时间计算中的惩罚项设置为γ = 3,将正则化参数设置为λ =10-6。
。我们将学习率设置为η = 0.2,将目标发放时间计算中的惩罚项设置为γ = 3,将正则化参数设置为λ =10-6。
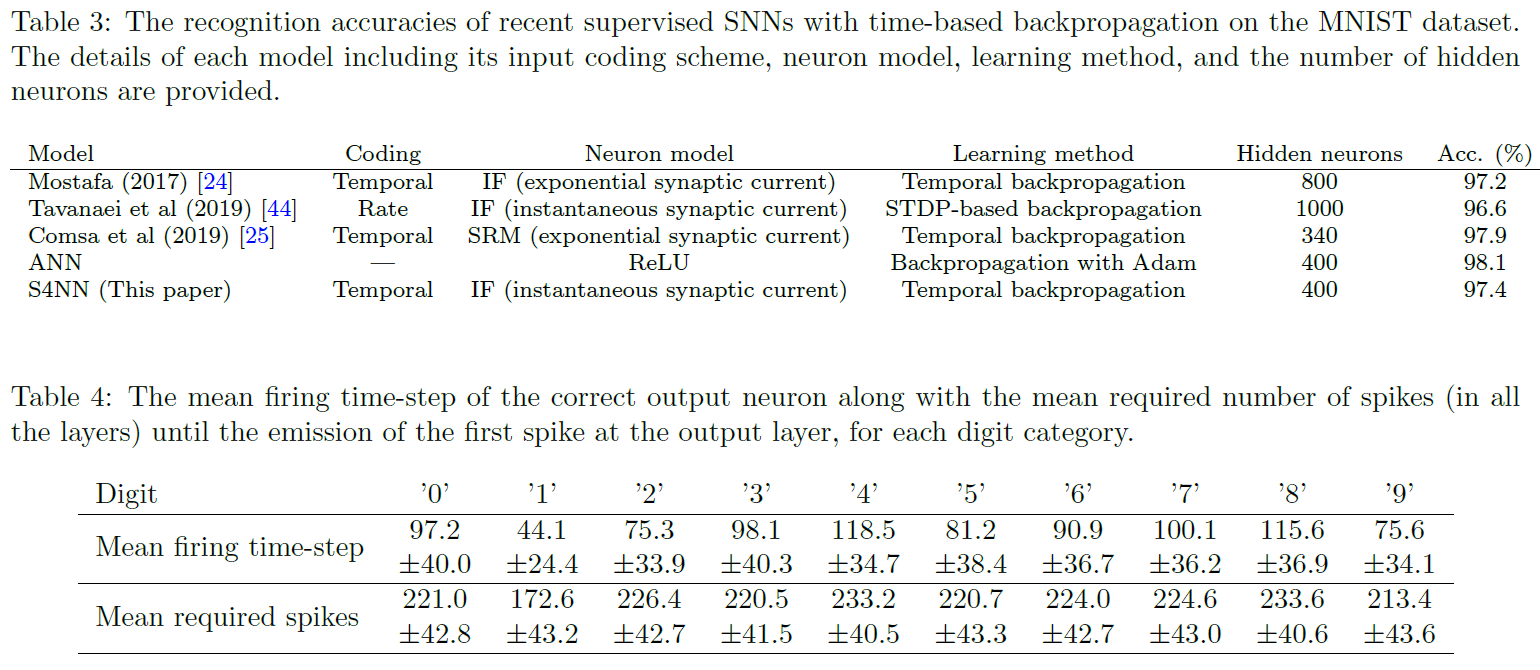
表3提供了MNIST数据集上所提出的S4NN (97.4±0.2%)和其他最近的SNN的分类精度,这些SNN具有基于脉冲时间的监督学习规则。在Mostafa (2017)[24]中,使用具有指数突触函数的800个IF神经元会使网络的神经处理和学习过程变得复杂。在Tavanaei et al. (2018)[44],由于使用发放率编码和1000个隐含神经元,网络计算成本非常高。在Comsa et al. (2019)[25]中,复杂的SRM神经元模型和α突触电流的使用使其难以基于事件进行实现。Comsa et al. (2019)提出的模型在慢速和快速机制下工作。在快速状态下,网络以97.4%的精度做出快速决策;在慢速状态下,网络达到97.9%的精度,但响应时间更长。S4NN的优点是使用简单的神经元模型(具有瞬时突触电流的IF),每个神经元最多具有一个脉冲的时序编码以及简单的监督时序学习规则。此外,我们在隐含层中仅使用了400个神经元,这使其比其他网络更轻量。
我们还实现了具有400个隐含单元的三层ANN(输入-隐含-输出)。我们对隐含层和输出层都使用ReLU激活函数,并采用均方误差(MSE)作为损失函数。我们使用Adam优化器对网络进行训练,并在MNIST上达到了98.1%的精度。尽管ANN的性能优于表3中的所有SNN模型,但SNN的优势在于其能源效率和硬件友好性。
图9在不同数字类别的图像上显示了每个输出神经元的平均发放时间。如图所示,对于每个数字类别,正确输出神经元的平均发放时间与其他神经元的发放时间之间都存在巨大差距。发放时间为44.1和118.5的数字"1"和"4"分别具有最小和最大平均发放时间。假设地,与其他数字相比,识别数字"1"所依赖的脉冲要少得多,并且响应速度会快得多。数字"4"(或平均发放时间为101.5的数字"8")需要更多的输入脉冲信号才能从其他(相似的数字)正确识别。有趣的是,平均而言,网络需要172.69个脉冲才能识别数字"1",而需要233.22个脉冲才能识别数字"4"。表4列出了正确输出神经元的平均发放时间以及所需的平均发放次数。请注意,所需的脉冲是通过计算所有三个层(输入,隐含和输出)中的脉冲数量直到在输出层发放第一个脉冲而获得的。
平均而言,所提出的S4NN在89.7个时间步骤(最大仿真时间的35.17%)中以97.4%的精度做出决策,只有218.3个脉冲(784+400+10个可能脉冲的18.22%)。请注意,在网络做出决定之前,隐含的神经元平均会发出132.2±6.7个脉冲。因此,所提出的网络以快速,准确和稀疏的方式工作。
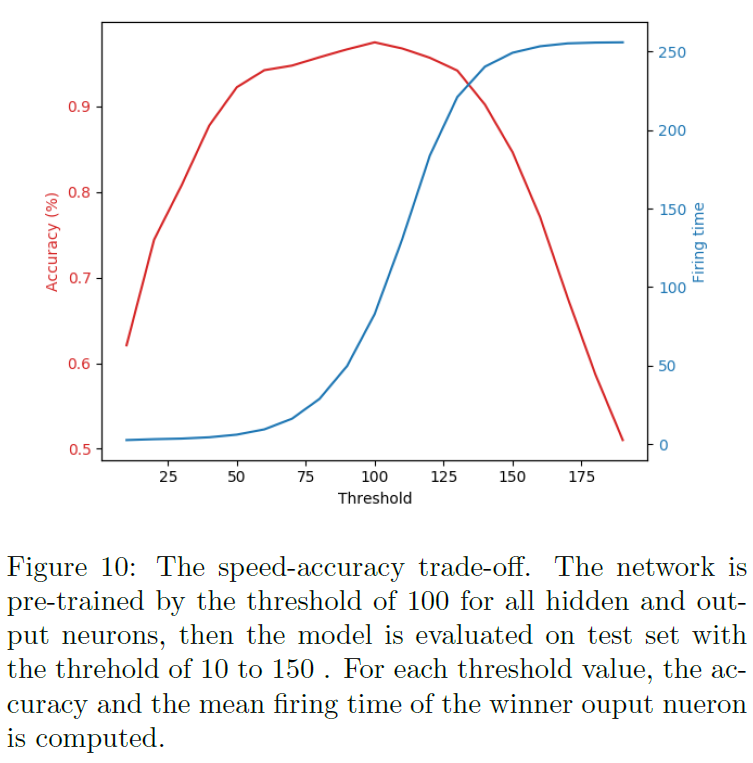
在进一步的实验中,我们评估了S4NN中的速度-精度权衡。为此,我们首先在MNIST上训练S4NN (所有神经元的阈值为100),并对其权重进行卷曲,然后将其所有隐含和输出神经元的阈值从10更改为150,并在测试集中对其进行评估。图10显示了获胜者输出神经元的精度和平均发放时间(即响应时间)超过不同的阈值。如图所示,通过增加阈值,精度提高,在阈值70之后达到94%以上,并在阈值100达到峰值。此外,可以看出,平均响应时间在阈值70之后迅速增长。平均响应时间对于阈值70,大约是15个时间步骤;对于阈值100,大约是89个时间步骤。因此,通过降低预训练网络的阈值,可以从S4NN获得更快但不太准确的响应。

4 Discussion
如今,SNN越来越流行[45, 46, 47, 48, 49, 50],它是研究大脑计算的最优工具之一[51, 52, 53, 54, 55, 56, 57, 58, 59]。在本文中,我们提出了一个SNN(称为S4NN),它由多层非泄漏IF神经元组成,具有首次脉冲时间编码和时序误差反向传播。关于视觉皮层中对象的快速处理(通常在100到150 ms范围内)以及从视网膜中感光器到颞下叶(IT)皮层中对象响应神经元至少有10个突触的事实,每个神经元只有大约10-15 ms来执行其计算,这对于发放率编码而言还不够[60]。此外,还表明,在图像呈现后大约100 ms内,IT皮质的第一波脉冲携带足够的信息以进行目标识别[61],表明了早期脉冲的重要性。此外,还有许多其他的神经生理学[62, 63]和计算[26, 27]证据支持首次脉冲编码的重要性。
根据我们采用的时序编码,输入神经元会发出一个脉冲,其延迟与相应的像素值成负比例,并且上游神经元最多只能发放出现一次。所提出的时序误差反向传播将正确的输出神经元推向更早发放(比起其他神经元)。它迫使网络以很少的脉冲(高稀疏度)做出快速准确的决策。我们在Caltech face/motorbike(精度99.2%)和MNIST(精度97.4%)数据集上的实验表明,与其他最近监督的SNN相比,S4NN具有更简单的神经元模型(即,非泄漏IF)准确解决目标识别任务的优点(与其他具有时序学习规则的最近监督SNN对比)。
让我们假设S4NN模型具有 l 层,其中n是网络最大层中神经元的数量。在基于时钟的实现中,对于任何层,可以在O(n2)中更新任何时间步骤的所有神经元的膜电位。因此,可以在O(l * n2 * t)中执行S4NN的前馈路径,其中 t 是输出层中第一个脉冲的时间步骤。请注意,所提出的时序反向传播会迫使网络尽可能早地准确响应。因此,所需的时间步骤 t 将比最大仿真时间小得多。注意,当时间步骤较短时,S4NN的实际计算时间可能会较短。
硬件实现不在本文讨论范围之内。但是,S4NN具有一些重要的功能,可能会使它对(数字)硬件更加友好。首先,计算仅限于每个神经元一个脉冲,并且在实践中,要在大多数神经元发放之前做出决定。相反,基于脉冲发放率的SNN需要更长的时间才能具有足够的输出脉冲来做出决定。因此,我们的方法在延迟方面和能量方面均具有优势,因为在大多数神经形态芯片上,能量消耗主要是由脉冲引起的[10]。其次,我们的方法是有效的记忆,因为一旦神经元发放,我们就可以忘记它的状态,然后将相应的记忆重新用于其他神经元。注意,每个神经元最多有一个脉冲的其他方法也共享这三个优点[24, 25, 34, 64]。但是我们的神经元模型要简单得多:没有泄漏,并且突触是瞬时的,如下所述,这使其对硬件更友好。在此,我们首次显示了反向传播可以适应这种简单的神经元模型,即使这需要一些近似(公式6)。
如果可以利用晶体管或电容器的物理特性在模拟硬件中有效地实现泄漏[9],则数字硬件中的泄漏总是很昂贵的。两种方法已经被提出。所有神经元的电压都周期性地降低,例如每毫秒降低一次(参见例如[65])。显然,这种方法非常耗能。泄漏也可以基于事件的方式来处理:当接收到输入脉冲时,要考虑到泄漏,该泄漏基于自上一次输入脉冲以来的经过时间(例如,参见[66, 67])。但这需要存储每个神经元的最后输入脉冲时间,这会增加内存占用量。最后,瞬时突触是迄今为止处理起来最简单的突触:每个输入脉冲都会导致准时电位增加。基于电流或基于电导的突触需要状态参数,并且每个输入脉冲都会使电压在几个连续的时间步骤上更新。
由于脉冲神经元在其发放时间的阈值激活函数具有不可微分性,因此将梯度下降和反向传播算法应用于SNN一直是一个很大的挑战。不同的研究提出了不同的技术,包括基于发放率的可微激活函数[13, 14, 15],平滑的脉冲生成器[16]和替代梯度[8, 17, 18, 19, 20, 21]。所有这些方法都不能处理脉冲时间。在称为延迟学习的最后一种方法中,神经元活动是基于其发放时间(通常是首次脉冲)来定义的,与之前的三种方法相反,不需要推导阈值激活函数。但是,他们需要根据神经元膜电位或突触前神经元的发放时间来定义神经元的发放时间,并在反向传播过程中使用其推导。例如,在Spikeprop[23]中,作者使用线性近似函数,该函数依赖于发放时间附近膜电位的变化(因此,他们不能使用IF神经元模型)。另外,在Mostafa (2017)[24]中,作者通过使用指数衰减的突触,直接根据突触前神经元的发放时间来定义神经元的发放时间。在此,通过假设发放时间和膜电位之间的单调递增线性关系,我们可以在所提出的S4NN模型中使用具有瞬时突触的IF神经元。
具有延迟学习的SNN使用单脉冲时间编码,因此,如果神经元未达到其阈值,则会出现问题,因为这样就无法确定延迟。有多种不同方法可以解决此问题。在Mostafa (2017)[24]中,作者使用非泄漏神经元并确保权重之和大于阈值,或者在Comsa (2019)[25]中,作者使用假输入"同步脉冲"来推动神经元超过阈值。在所提出的S4NN中,我们假设如果神经元在仿真过程中没有发放,它将在仿真后的某个时候发放,因此,我们迫使它在最后一个时间步骤发出假脉冲。
在此,我们只是在图像分类任务上测试S4NN,以后的研究可以在其他数据模态上测试S4NN。如Caltech face/motorbike数据集所示,所提出的学习规则具有可扩展性,可用于更深的S4NN架构。而且,它可以用于卷积脉冲神经网络(CSNN)。当前的CSNN主要从传统CNN转换,其发放率为[68, 69, 70, 71]和时序编码[72]。尽管这些网络的精度很好,但就计算成本或时间而言,它们可能无法有效地发挥作用。利用基于脉冲的反向传播开发CSNN的最新成果已经在不同的数据集上产生了令人印象深刻的结果[73, 74],但是,他们使用了昂贵的神经元模型和发放率编码方案。因此,将所提出的S4NN扩展到卷积架构可以提供较大的计算优势。这种方式最重要的挑战是防止卷积层中权重共享约束下的梯度消失/爆炸和学习。但是,与基于发放率的CSNN不同,可以通过传播每个池化神经元感受野内出现的首次脉冲来简单地完成最大池化操作。
此外,尽管SNN比传统的ANN在硬件上更友好,但受监督的SNN中的反向传播过程并不容易在硬件中实现。最近,使用可在S4NN中使用的脉冲[75]来估计反向传播,使其更适合于硬件实现。



