Proximal Policy Optimization Algorithms
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

arXiv: Learning, (2017)
Abstract
我们提出了一系列用于RL的策略梯度方法,该方法在通过环境交互进行数据采样与使用随机梯度上升优化"替代"目标函数之间交替进行。尽管标准策略梯度方法对每个数据样本执行一个梯度更新,但我们提出了一种新颖的目标函数,该函数可实现多个批次的小批量更新。我们称为邻近策略优化(PPO)的新方法具有信任域策略优化(TRPO)的某些优点,但它们实现起来更简单,更通用,并且具有更好的样本复杂性(凭经验)。我们的实验在一系列基准任务上测试了PPO,包括模拟的机器人运动和Atari游戏玩法,我们证明PPO的性能优于其他在线策略梯度方法,并且总体上在样本复杂性,简单性和有效时间之间取得了良好的平衡。
1 Introduction
近年来,已经提出了几种不同的方法来利用神经网络函数近似进行RL。主要的竞争者是深度Q学习[Mni+15],"幼稚"策略梯度方法[Mni+16]和信任域/自然策略梯度方法[Sch+15b]。但是,在开发可扩展(适用于大型模型和并行实现),数据高效且鲁棒(即在无需超参数调整的情况下成功解决各种问题)的方法方面,仍有改进的余地。Q学习(带有函数近似)在许多简单的问题上失败了1,并且了解甚少,幼稚策略梯度法的数据效率和鲁棒性很差;信任域策略优化(TRPO)相对复杂,并且与包含噪声(例如,随机失活)或参数共享(在策略和价值函数之间,或与辅助任务)的结构不兼容。
本文旨在通过引入一种仅使用一阶优化即可达到TRPO的数据效率和可靠性能的算法来改进当前的事务状态。我们提出了一种具有截断的概率比的新颖目标,该目标形成了策略性能的悲观估计(即下限)。为了优化策略,我们在从策略采样数据和对采样数据执行几个优化epoch之间交替进行。
我们的实验比较了替代目标的各种不同版本的性能,发现具有截断的概率比的版本性能最优。我们还将PPO与文献中的几种先前算法进行比较。在连续控制任务上,它的性能优于我们所比较的算法。在Atari上,它的性能(就样本复杂性而言)比A2C好得多,并且与ACER类似,尽管它要简单得多。
1虽然DQN在具有离散动作空间的Arcade学习环境[Bel+15]等游戏环境中运行良好,但尚未证明在OpenAI Gym [Bro+16]等连续控制基准中表现良好,Duan et al.对此进行了描述[Dua+16]。
2 Background: Policy Optimization
2.1 Policy Gradient Methods
策略梯度方法通过计算策略梯度估计并将其插入随机梯度上升算法中来工作。最常用的梯度估计具有以下形式:

其中,πθ是随机策略,![]() 是时间步骤 t 的优势函数估计。在此,期望
是时间步骤 t 的优势函数估计。在此,期望![]() 表示在采样和优化之间交替的算法中,有限批次样本的经验平均值。使用自动微分软件的实现通过构造一个目标函数来工作,该目标函数的梯度是策略梯度估计;通过微分目标获得估计
表示在采样和优化之间交替的算法中,有限批次样本的经验平均值。使用自动微分软件的实现通过构造一个目标函数来工作,该目标函数的梯度是策略梯度估计;通过微分目标获得估计![]() :
:
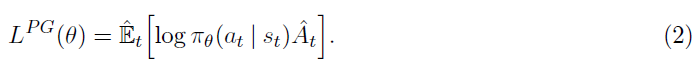
尽管使用相同的轨迹对此损失LPG进行多步优化很有吸引力,但是这样做并没有充分的理由,而且从经验上讲,它通常会导致破坏性的大策略更新(请参阅第6.1节;未显示结果,但结果与"无截断或惩罚"设置相似或更糟糕)。
2.2 Trust Region Methods
在TRPO [Sch+15b]中,目标函数("替代"目标)在策略更新大小受限的情况下被最大化。特别,

在此,θold是更新之前策略参数的向量。在对目标进行线性近似并对约束进行二次近似之后,可以使用共轭梯度算法有效地解决该问题。
证明TRPO合理的理论实际上建议使用惩罚而不是约束,即解决无约束的优化问题:
 (对于一些系数β) 这源于以下事实:某个替代目标(该替代目标计算状态上的最大KL而不是均值)为策略π的性能下限(即悲观界限)。TRPO使用硬约束而不是惩罚,因为很难选择在不同问题上甚至在特征随学习过程变化的单个问题中表现良好的单个β值。因此,为了实现模拟TRPO单调改进的一阶算法的目标,实验表明,仅仅选择固定的惩罚因子β并利用SGD优化惩罚目标等式(5)是不够的;需要额外的修改。
(对于一些系数β) 这源于以下事实:某个替代目标(该替代目标计算状态上的最大KL而不是均值)为策略π的性能下限(即悲观界限)。TRPO使用硬约束而不是惩罚,因为很难选择在不同问题上甚至在特征随学习过程变化的单个问题中表现良好的单个β值。因此,为了实现模拟TRPO单调改进的一阶算法的目标,实验表明,仅仅选择固定的惩罚因子β并利用SGD优化惩罚目标等式(5)是不够的;需要额外的修改。
3 Clipped Surrogate Objective
令rt(θ)表示概率比![]() ,因此r(θold) = 1。TRPO使"替代"目标最大化:
,因此r(θold) = 1。TRPO使"替代"目标最大化:
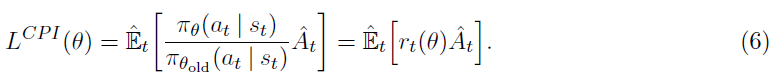
上标CPI指的是保守的策略迭代[KL02],其中提出了这一目标。若是没有限制,LCPI的最大化将导致策略更新过大;因此,我们现在考虑如何修改目标,以惩罚将rt(θ)远离1的策略更改。
我们提出的主要目标如下:
![]()
其中ε是一个超参数,例如ε = 0.2。该目标的动机如下。最小值内的第一项是LCPI。第二项,![]() ,通过截断概率比来修改替代目标,从而消除了将rt移到区间[1-ε, 1+ ε]之外的动机。最后,我们采用了已截断和未截断目标的最小值,因此最终目标是未截断目标的下限(即悲观界限)。使用此方案,我们仅在概率比提高目标时才忽略它的变化,而在它使目标恶化时才将其包括在内。请注意,LCLIP(θ) = LCPI(θ)是θold附近的一阶(即r = 1),但是随着θ远离θold,它们会变得不同。图1绘制了LCLIP中的一个项(即单个 t );注意,根据优势是正或负,概率比 r 裁剪为1-ε或1+ε。
,通过截断概率比来修改替代目标,从而消除了将rt移到区间[1-ε, 1+ ε]之外的动机。最后,我们采用了已截断和未截断目标的最小值,因此最终目标是未截断目标的下限(即悲观界限)。使用此方案,我们仅在概率比提高目标时才忽略它的变化,而在它使目标恶化时才将其包括在内。请注意,LCLIP(θ) = LCPI(θ)是θold附近的一阶(即r = 1),但是随着θ远离θold,它们会变得不同。图1绘制了LCLIP中的一个项(即单个 t );注意,根据优势是正或负,概率比 r 裁剪为1-ε或1+ε。

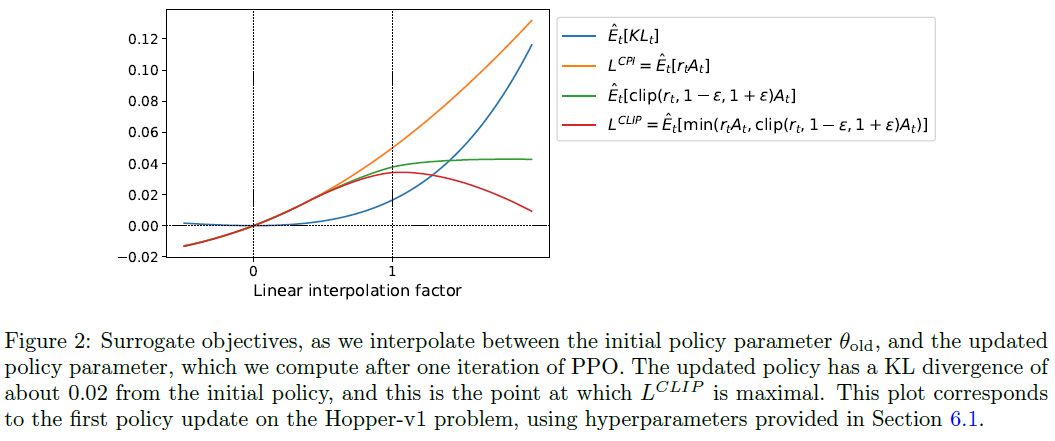
图2提供了关于替代目标LCLIP的另一种直觉来源。它显示了当我们沿着策略更新方向进行插值时,几个目标是如何变化的,这是通过对连续控制问题进行邻近策略优化(稍后将介绍的算法)获得的。我们可以看到,LCLIP是LCPI的下限,并且会因策略更新过大而受到惩罚。
4 Adaptive KL Penalty Coefficient
可以替代或添加到截断替代目标的另一种方法是对KL散度使用惩罚,并调整惩罚因子,以便我们在每个策略更新都达到KL散度dtarg的一些目标价值。在我们的实验中,我们发现KL惩罚的性能比截断替代目标更差,但是,由于它是重要的基准,因此我们将其包括在此处。
在此算法的最简单实例中,我们在每个策略更新中执行以下步骤:
- 使用几个小批量SGD的epoch,优化KL惩罚的目标:
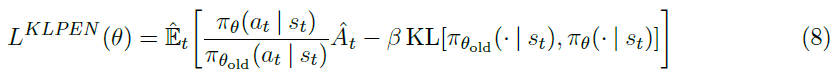
- 计算
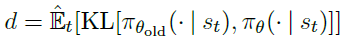

更新后的β被用于下一次策略更新。通过此方案,我们偶尔会看到策略更新,其中KL散度与dtarg显著不同,但是这些更新很少,并且β会迅速调整。上面的参数1.5和2是通过试探法选择的,但是算法对其并不十分敏感。β的初始值是另一个超参数,但在实践中并不重要,因为该算法会对其进行快速调整。
5 Algorithm
可以通过对典型的策略梯度实现方案进行较小的更改来计算和微分前几部分中的替代损失。对于使用自动微分的实现,只需简单地构造损失LCLIP或LKLPEN而不是LPG,就可以实现此目标的随机梯度上升的多个步骤。
用于计算方差减少的优势函数估计量的大多数技术都使用学到的状态价值函数V(s);例如,广义优势估计[Sch+15a]或[Mni+16]中的有限视野估计。如果使用在策略和价值函数之间共享参数的神经网络结构,我们必须使用将策略替代和价值函数误差项组合在一起的损失函数。如过去的工作所提出的,可以通过增加熵奖励以确保足够的探索来进一步增强此目标[Wil92; Mni+16]。结合这些项,我们获得以下目标,每次迭代中该目标(近似)为最大:
![]()
其中c1,c2是因子,S表示熵奖励,![]() 是平方误差损失
是平方误差损失![]() 。
。
一种策略梯度实现方式,在[Mni+16]中流行并且非常适合与循环神经网络一起使用,对 T 个时间步骤运行策略(其中 T 远小于回合长度),并将收集的样本用于更新。这种方式需要一个视野不超过时间步骤 T 的优势估计器。[Mni+16]使用的估计器为:
![]()
其中 t 在给定长度 T 的轨迹段内指定[0, T]中的时间索引。推广此选择,我们可以使用广义优势估计的截断形式,当λ = 1时,可简化为等式(10)。
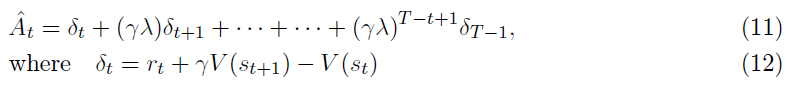
下面显示了使用固定长度轨迹段的邻近策略优化(PPO)算法。每次迭代,N个(并行)actor中的每一个都收集 T 个时间步骤的数据。然后,我们在这些NT个时间步骤的数据上构建替代损失,并使用小批量SGD(或通常是为了获得更好的性能,Adam [KB14])对K个epoch进行优化。

6 Experiments
6.1 Comparison of Surrogate Objectives
首先,我们比较了不同超参数下的几个不同的替代目标。在此,我们将替代目标LCLIP与几种自然变体和消融版本进行比较。
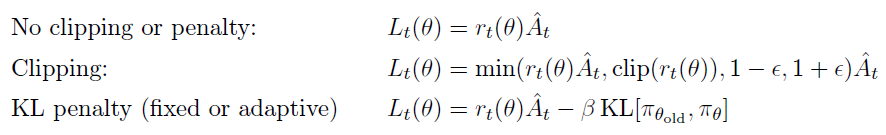
对于KL惩罚,可以使用目标KL价值dtarg使用第4节中所述的固定惩罚因子β或自适应因子。请注意,我们还尝试了在log空间中进行裁剪,但是发现性能并不好。
因为我们正在为每个算法变体搜索超参数,所以我们选择了计算上便宜的基准来测试算法。即,我们使用了在OpenAI Gym [Bro+16]中实现的7个仿真机器人任务2,这些任务使用MuJoCo [TET12]物理引擎。每个任务都要进行一百万次训练。除了我们搜索过的用于裁剪(ε)的超参数和KL惩罚(β, dtarg)外,表3还提供了其他超参数。
为了表示该策略,我们使用了一个全连接的MLP,该MLP具有两个64个单位的隐含层和tanh非线性,遵循[Sch+15b; Dua+16],输出带有可变标准差的高斯分布均值。我们不会在策略和价值函数之间共享参数(因此因子c1是无关的),并且我们不会使用熵奖励。
每种算法都在所有7个环境上运行,每个环境上都有3个随机种子。我们通过计算最近100个回合的平均总奖励,对算法的每次运行进行了评分。我们对每种环境的得分进行了调整和缩放,以使随机策略的得分为0,最优结果设置为1,并在21次运行中取均值,以针对每种算法设置生成单个标量。
结果显示在表1中。请注意,对于设置没有裁剪或惩罚的设置,该分数是负的,因为在一个环境(half cheetah)下它会导致非常负的分数,这比初始的随机策略还差。
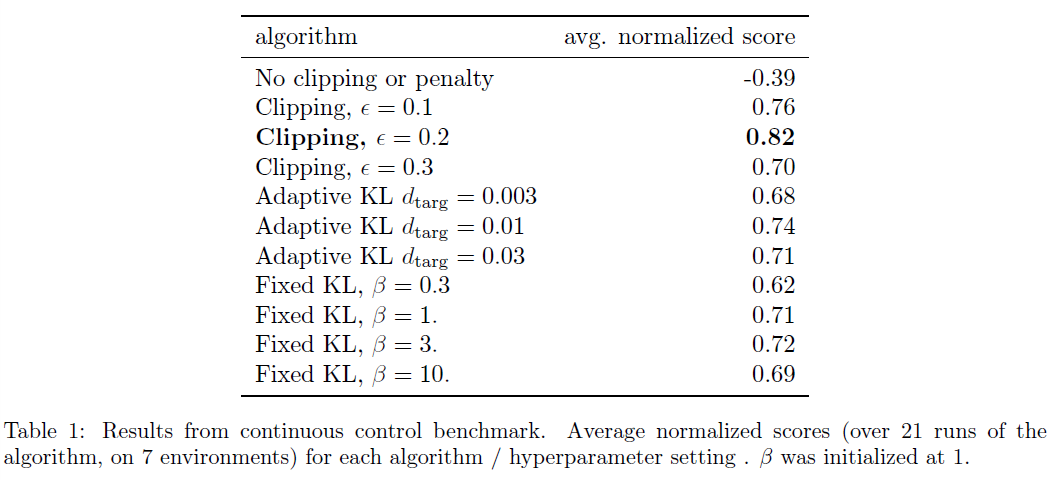
2HalfCheetah, Hopper, InvertedDoublePendulum, InvertedPendulum, Reacher, Swimmer, and Walker2d, all “-v1”
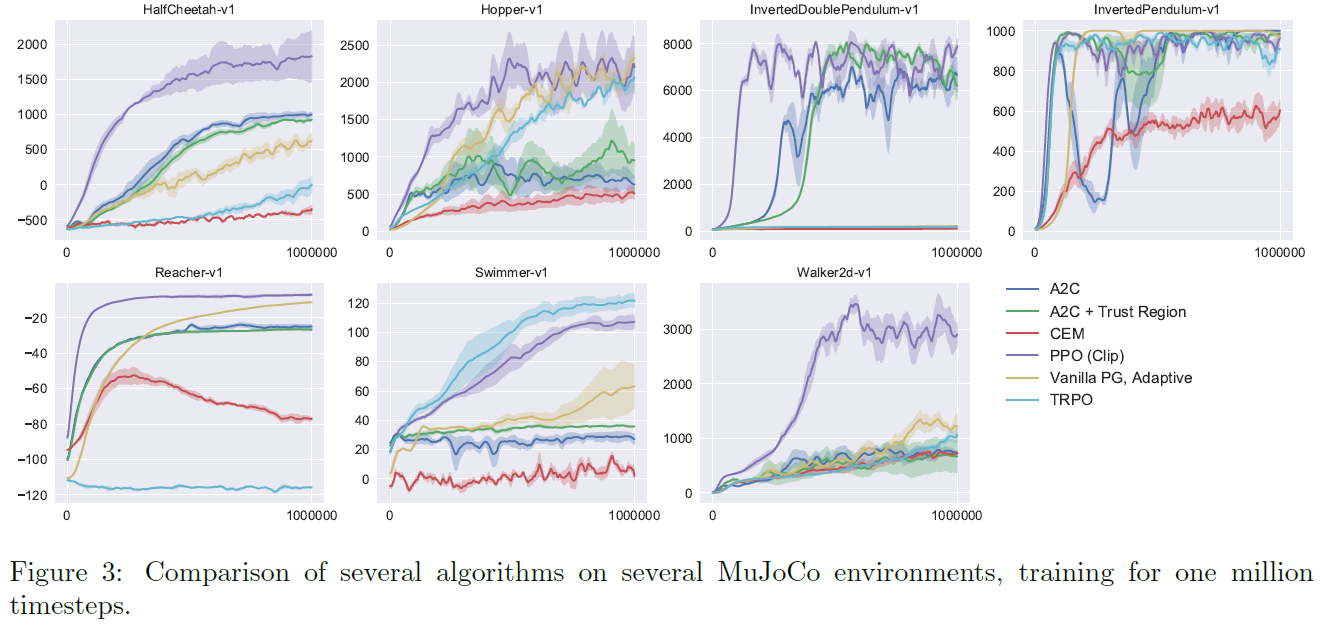
6.2 Comparison to Other Algorithms in the Continuous Domain
接下来,我们将PPO(具有第3节中的"截断"替代目标)与文献中的其他几种方法进行比较,这些方法被认为对于连续性问题是有效的。我们比较了以下算法的调整实现:信任域策略优化[Sch+15b],交叉熵方法(CEM)[SL06],具有自适应步长3的幼稚策略梯度,A2C [Mni+16],具有信任域的A2C [Wan+16]。A2C代表优势actor-critic,并且是A3C的同步版本,我们发现它具有与异步版本相同或更好的性能。对于PPO,我们使用上一节中的超参数(ε = 0.2)。我们看到,在几乎所有连续控制环境中,PPO的性能都优于以前的方法。
3在每一批数据后,使用与第4节中所示相似的规则,根据原始策略和更新策略的KL散度来调整Adam步长。可在https://github.com/berkeleydeeprlcourse/homework/tree/master/hw4获得实现。
6.3 Showcase in the Continuous Domain: Humanoid Running and Steering
为了展示PPO在高维连续控制问题上的性能,我们对一系列涉及3D humanoid的问题进行了训练,在这种问题中,机器人必须运行,转向并从地面上站起来,可能会受到立方体的撞击。我们测试的三个任务是(1) RoboschoolHumanoid:仅向前运动;(2) RoboschoolHumanoidFlagrun:每200个时间步骤或达到目标时,目标位置就会随机变化;(3) RoboschoolHumanoidFlagrunHarder,其中机器人被立方体撞击,并需要从地面站起来。有关学到的策略的静止帧,请参见图5;有关这三个任务的学习曲线,请参见图4。表4中提供了超参数。在并发工作中,Heess et al. [Hee+17]使用PPO的自适应KL变体(第4节)来学习3D机器人的运动策略。


6.4 Comparison to Other Algorithms on the Atari Domain
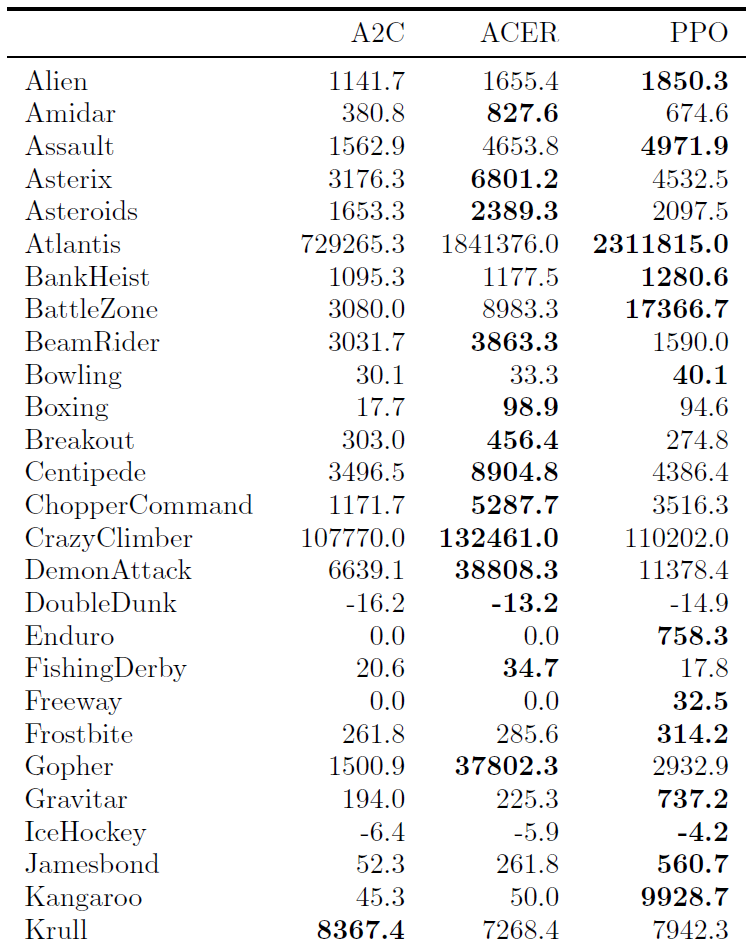
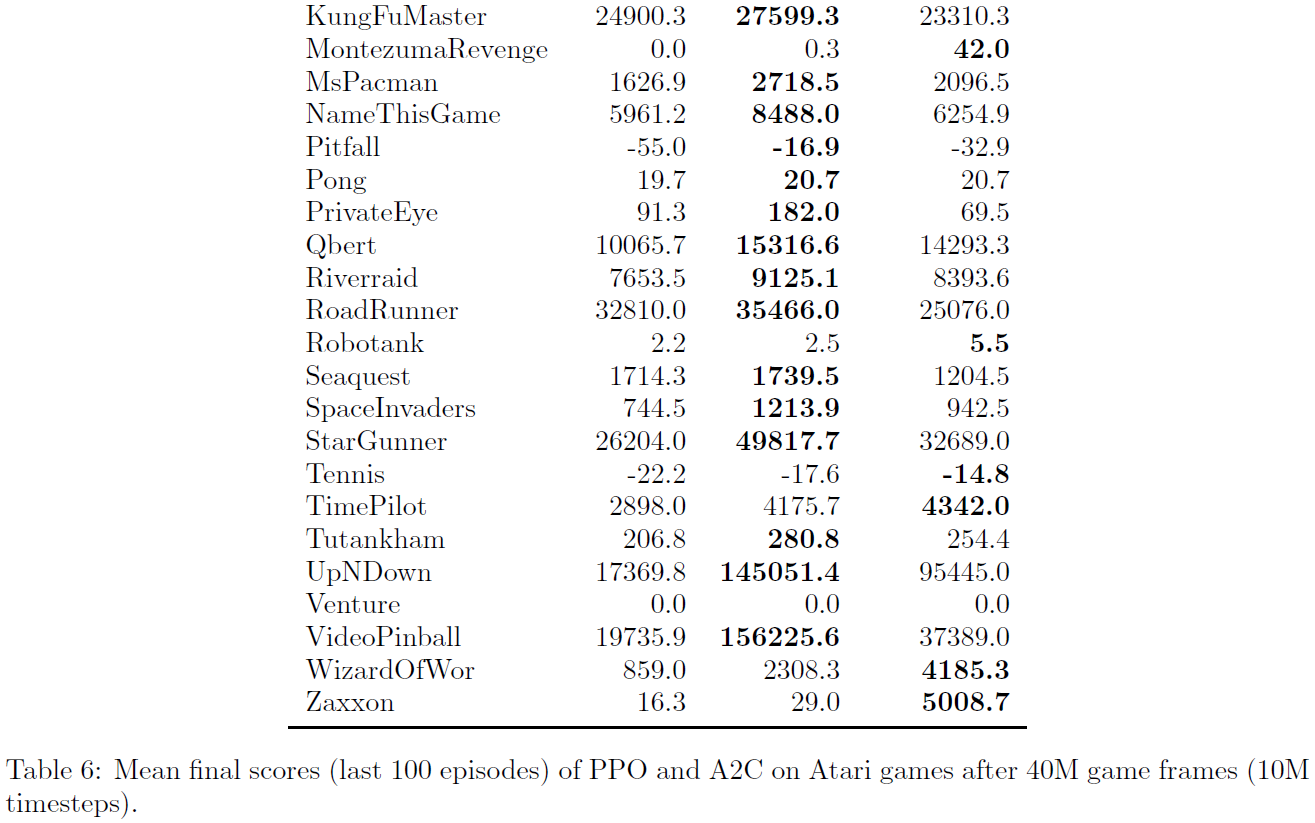
我们还在Arcade学习环境[Bel+15]基准上运行了PPO,并将其与经过调整的A2C [Mni+16]和ACER [Wan+16]的实现进行了比较。对于这三种算法,我们使用与[Mni+16]中使用的策略网络结构相同的策略。表5中提供了PPO的超参数。对于其他两种算法,我们使用了经过优化的超参数,以使该基准上的性能最大化。
附录B中提供了所有49个游戏的结果和学习曲线表。我们考虑以下两个得分指标:(1) 在整个训练期间每个回合的平均奖励(偏向快速学习),以及(2) 最近100个回合的训练中每个回合的平均奖励(偏向最终性能)。表2显示了每种算法"获胜"的游戏数量,我们通过对三个试验的得分指标求平均来计算获胜者。

7 Conclusion
我们介绍了邻近策略优化,这是一系列策略优化方法,它们使用多个随机梯度上升epoch来执行每个策略更新。这些方法具有信任域方法的稳定性和可靠性,但实现起来要简单得多,仅需几行代码即可更改为原始策略梯度实现,适用于更常规的设置(例如,当对策略和价值函数使用联合结构时),并具有更好的整体性能。
A Hyperparameters


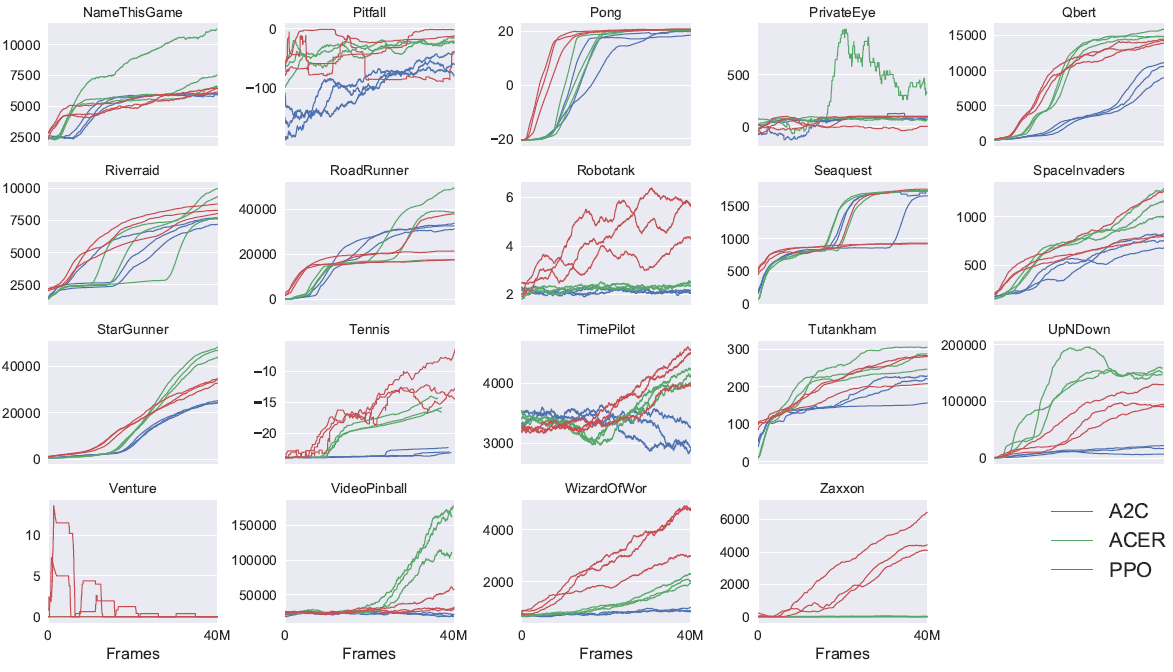
B Performance on More Atari Games
在此,我们比较了49个Atari游戏中PPO与A2C的比较。 图6显示了三个随机种子各自的学习曲线,而表6显示了平均性能。