Asynchronous Methods for Deep Reinforcement Learning
郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
ICML 2016
Abstract
我们提出了一个概念上简单且轻量级的深度强化学习框架，该框架使用异步梯度下降来优化深度神经网络控制器。我们提出了四种标准强化学习算法的异步变体，并表明并行参与者学习器对训练具有稳定作用，允许所有四种方法成功训练神经网络控制器。性能最佳的方法是actor-critic的异步变体，它超越了Atari领域的当前最先进技术，同时在单个多核CPU而不是GPU上训练了一半的时间。此外，我们展示了异步actor-critic在各种连续电机控制问题以及使用视觉输入导航随机3D迷宫的新任务上取得了成功。
1. Introduction
深度神经网络提供了丰富的表征，可以使RL算法有效执行。但是，以前认为简单的在线RL算法与深度神经网络的组合从根本上来说是不稳定的。取而代之的是，已经提出了多种解决方案来稳定算法 (Riedmiller, 2005; Mnih et al., 2013; 2015; Van Hasselt et al., 2015; Schulman et al., 2015a)。这些方法有一个共同的想法：在线RL智能体遇到的观测数据的序列是不稳定的，并且在线RL更新是高度相关的。通过将智能体的数据存储在经验回放内存中，可以对数据进行批处理 (Riedmiller, 2005; Schulman et al., 2015a)或从不同的时间步骤随机采样 (Mnih et al., 2013; 2015; Van Hasselt et al., 2015)。以这种方式在内存上进行汇聚可减少非稳定性并去除更新相关性，但同时将方法限制为异策强化学习算法。
基于经验回放的深度RL算法在诸如Atari 2600这样具有挑战性的领域中取得了空前的成功。但是，经验回放有几个缺点：每次真正的交互都会使用更多的内存和计算量；并且需要异策学习算法，该算法可以从较旧的策略生成的数据中进行更新。
在本文中，我们为深度强化学习提供了非常不同的范例。代替经验回放，我们在环境的多个实例上异步并行执行多个智能体。这种并行性还将智能体的数据去相关到一个更平稳的过程中，因为在任何给定的时间步骤，并行智能体将经历各种不同的状态。这个简单的想法可以使用深度神经网络来鲁棒且有效地应用更多种类的基本同策RL算法，例如Sarsa，n步方法和actor-critic方法，以及异策RL算法 (例如Q学习)。
我们的并行强化学习范例也提供了实际的好处。以往的深度强化学习方法严重依赖于专用硬件，例如GPU(Mnih et al., 2015; Van Hasselt et al., 2015; Schaul et al., 2015)或大规模分布式架构 (Nair et al., 2015)，我们的实验在一台带有标准多核CPU的计算机上运行。当将其应用于各种Atari 2600域时，在许多游戏中，异步强化学习可在比先前基于GPU的算法更少的时间内获得更好的结果，并且所使用的资源比大规模分布的方法少得多。我们所提出的最优方法，异步优势actor-critic(A3C)，还掌握了各种连续的电机控制任务，并学会了仅从视觉输入中探索3D迷宫的一般策略。我们相信，A3C在2D和3D游戏，离散和连续动作空间上的成功以及对前馈和循环智能体进行训练的能力使其成为迄今为止最通用且最成功的强化学习智能体。
2. Related Work
3. Reinforcement Learning Background
我们考虑标准的强化学习设置，其中智能体在多个离散时间步骤上与环境ε交互。在每个时间步骤 t，智能体接收状态st并根据其策略π从一组可能的动作A中选择一个动作at，其中π是从状态st到动作at的映射。作为回报，智能体接收下一个状态st+1并接收标量奖励rt。该过程继续进行，直到智能体达到终止状态，然后该过程重新启动。回报
是带折扣因子γ ∈ (0, 1]的时间步骤 t 的总累积回报，智能体的目标是使每个状态st的期望回报最大化。
动作价值Qπ(s, a) = E[Rt|st = s, a]是在状态s和后续策略π中选择动作a的期望回报。最优价值函数Q*(s, a) = maxπ Qπ(s, a)给出状态s和任何策略均可得到的动作a的最大动作价值。类似地，策略π下状态s的价值被定义为V*(s) = E[Rt|st = s]，并且仅仅是从状态s遵循后续策略π的期望回报。
在基于价值的无模型强化学习方法中，使用函数近似(例如神经网络)来表示动作价值函数。令Q(s, a; θ)是带有参数θ的近似动作-价值函数。θ的更新可以从各种强化学习算法中得出。这种算法的一个示例是Q学习，其目的是直接近似最优动作价值函数：Q*(s, a) ≈ Q(s, a; θ)。在单步Q学习中，通过迭代最小化一系列损失函数来学习动作价值函数Q(s, a; θ)的参数θ，其中第 i 个损失函数定义为
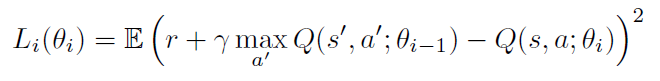
其中s'是状态s之后遇到的状态。
我们将上述方法称为单步Q学习，因为它向单步回报r + γ maxa' Q(s', a'; θ)更新动作价值Q(s, a)。使用单步方法的一个缺点是，获得奖励 r 仅直接影响状态动作对s, a的价值，这导致奖励。其他状态动作对的价值仅通过更新后的价值Q(s, a)间接影响。这可能会使学习过程变慢，因为需要进行许多更新才能将奖励传播到相关的先前状态和动作。
一种更快地传播奖励的方法是使用n步回报(Watkins, 1989; Peng＆Williams, 1996)。在n步Q学习中，朝定义为rt + γrt+1 + … + γn-1rt+n-1 + maxa γnQ(st+n, a)的n步回报更新Q(s, a)。这导致单个奖励 r 直接影响n个先前状态动作对的价值。这使得将奖励传播到相关状态-动作对的过程可能会更加有效。
与基于价值的方法相反，基于策略的无模型方法直接对策略π(a|s; θ)进行参数化，并通过对E[Rt]执行(通常是近似的)梯度上升来更新参数。这种方法的一个例子是由Williams (1992)提出的REINFORCE算法族。标准REINFORCE在
方向上更新策略参数θ，这是
的无偏估计。通过从回报中减去状态bt(st)的已知函数(被称为基准)，可以减少此估计的方差，同时保持其无偏。所得的梯度为
。
通常将学到的价值函数估计用作基准bt(st) ≈ Vπ(st)，从而导致更低的策略梯度的方差估计。当近似价值函数用作基准时，用于缩放策略梯度的量Rt - bt可以视为状态st时动作at的优势估计，或者A(at, st) = Q(at, st) - V(st)，因为Rt是对Qπ(at, st)的估计，而bt是对Vπ(st)的估计。可以将这种方法视为一种actor-critic结构，其中策略π是actor，基准bt是critic (Sutton＆Barto, 1998; Degris et al., 2012)。
4. Asynchronous RL Framework
我们现在介绍单步Sarsa、单步Q-learning、n步Q-learning和优势actor-critic的多线程异步变体。设计这些方法的目的是找到能够可靠地训练深度神经网络策略且无需大量资源的RL算法。虽然底层的RL方法完全不同，actor-critic是一种同策的策略搜索方法，而Q-learning是一种基于异策价值的方法，但鉴于我们的设计目标，我们使用两个主要思想来使所有四种算法都实用。
首先，我们使用异步actor学习者，类似于Gorila框架(Nair et al., 2015)，但我们没有使用单独的机器和参数服务器，而是在单台机器上使用多个CPU线程。将学习器保持在一台机器上消除了发送梯度和参数的通信成本，并使我们能够使用Hogwild! (Recht et al., 2011)训练的风格更新。
其次，我们观察到并行运行的多个actor学习者可能正在探索环境的不同部分。此外，可以在每个actorx学习者中明确使用不同的探索策略来最大化这种多样性。通过在不同的线程中运行不同的探索策略，多个actor学习者并行应用在线更新对参数所做的整体更改可能比单个智能体应用在线更新在时间上的相关性更小。因此，我们不使用回放缓存，而是依靠采用不同探索策略的并行actor来执行DQN训练算法中经验回放所承担的稳定角色。
除了稳定学习之外，使用多个并行的actor学习者还具有多种实际好处。首先，我们获得了训练时间的减少，这与并行actor学习者的数量大致呈线性关系。其次，由于我们不再依赖经验回放来稳定学习，我们能够使用诸如Sarsa和actor-critic之类的策略强化学习方法以稳定的方式训练神经网络。我们现在描述我们的单步Q-learning、单步Sarsa、n步Q-learning和优势actor-critic的变体。
Asynchronous one-step Q-learning: 算法1中显示了我们的Q学习变体的伪代码(我们称之为异步单步Q学习)，每个线程都与自己的环境副本交互，并在每一步计算Q学习损失的梯度。正如DQN训练方法中所提出的，我们使用共享且变化缓慢的目标网络来计算Q学习损失。在应用梯度之前，我们还会在多个时间步骤上累积梯度，这与使用小批量处理类似。这样可以减少多个actor学习器覆盖彼此更新的可能性。在几个步骤上累积更新还提供了一些权衡计算效率与数据效率的能力。
最后，我们发现为每个线程提供不同的探索策略有助于提高鲁棒性。以这种方式在探索中增加多样性通常也会通过更好的探索来提高性能。尽管有许多可能的方法可以使探索策略有所不同，但我们尝试使用ε-贪婪探索，并通过每个线程定期从某些分布中采样。
Asynchronous one-step Sarsa: 异步单步Sarsa算法与算法1中给出的异步单步Q学习相同，只是它对Q(s, a)使用不同的目标价值。单步Sarsa使用的目标价值为r + Q(s', a'; θ-)，其中a'是在状态s'下采取的动作(Rummery & Niranjan, 1994; Sutton & Barto, 1998)。我们再次使用目标网络，并在多个时间步骤上累积更新以稳定学习。
Asynchronous n-step Q-learning: 补充算法S2中显示了用于多步Q学习的变体的伪代码。该算法有些不寻常，因为它通过显式计算n步回报而在前向视图中运行，与资格迹等技术所使用的更常见的后向视图相反(Sutton＆Barto, 1998)。我们发现，在使用基于动量的方法和时间反向传播训练神经网络时，使用前向视图更容易。为了计算单个更新，该算法首先使用其探索策略选择动作(最多tmax个步骤或直到达到终止状态)。自从上次更新以来，此过程导致智能体从环境中接收最多tmax奖励。然后，该算法为自上次更新以来遇到的每个状态-动作对计算n步Q学习更新的梯度。每个n步更新都使用可能的最长n步回报，从而对最近的状态进行一步更新，对第二近的状态进行两步更新，依此类推，总共进行tmax次更新。累积的更新将在单个梯度步骤中应用。
Asynchronous advantage actor-critic: 该算法(我们称之为A3C)维护策略π(at|st; θ)和价值函数V(st; θv)的估计。就像我们的n步Q学习的变体一样，我们的actor-critic的变体也在前向视图中运行，并且使用n步回报的相同组合来更新策略和价值函数。策略和价值函数在每tmax个动作之后或达到终止状态时更新。该算法执行的更新可以看作是
，其中A(st, at; θ, θv)是对优势函数
的估计，其中k可能因状态而异，且以tmax为上限。该算法的伪代码在补充算法S3中提供。
与基于价值的方法一样，我们依靠并行的actor学习器和积累的更新来提高训练稳定性。请注意，尽管出于一般性考虑，策略的参数θ和价值函数的θv单独显示，但实际上我们总是共享某些参数。我们通常使用卷积神经网络，该神经网络对于策略π(at|st; θ)具有一个softmax输出，对于价值函数V(st; θv)具有一个线性输出，并且共享所有非输出层。
我们还发现，通过阻止过早收敛到次优确定性策略，可以将策略π的熵添加到目标函数中，从而改进了探索。该技术最初是由(Williams＆Peng, 1991)提出的，他发现该技术在需要分层行为的任务中特别有用。包含熵正则项的完整目标函数相对于策略参数的梯度采用
，其中H是熵。超参数控制熵正则项的强度。
Optimization: 我们在异步框架中研究了三种不同的优化算法——具有动量的SGD，没有共享统计信息的RMSProp(Tieleman＆Hinton, 2012)和具有共享统计信息的RMSProp。我们使用由下式提供的标准非中心RMSProp更新
其中所有操作均按元素执行。对Atari 2600游戏的子集进行的比较表明，在不同线程之间共享统计信息g的RMSProp变体比其他两种方法更鲁棒。有关方法和比较的全部详细信息，请参见补充第7节。
5. Experiments
我们使用四种不同的平台来评估所提出框架的属性。我们使用Arcade Learning Environment (Bellemare et al., 2012)进行大部分实验，该环境为Atari 2600游戏提供模拟器。这是RL算法最常用的基准环境之一。我们使用Atari域与最先进的结果进行比较(Van Hasselt et al., 2015; Wang et al., 2015; Schaul et al., 2015; Nair et al., 2015; Mnih et al., 2015)，以及对所提出的方法进行详细的稳定性和可扩展性分析。我们使用TORCS 3D赛车模拟器(Wymann et al., 2013)进行了进一步的比较。我们还使用两个额外的域来仅评估A3C算法——Mujoco和Labyrinth。MuJoCo (Todorov, 2015)是一个物理模拟器，用于评估具有接触动力学的连续运动控制任务的智能体。Labyrinth是一个新的3D环境，智能体必须学习从视觉输入中随机生成的迷宫中寻找奖励。我们的实验设置的精确细节可以在补充第8节中找到。
5.1. Atari 2600 Games
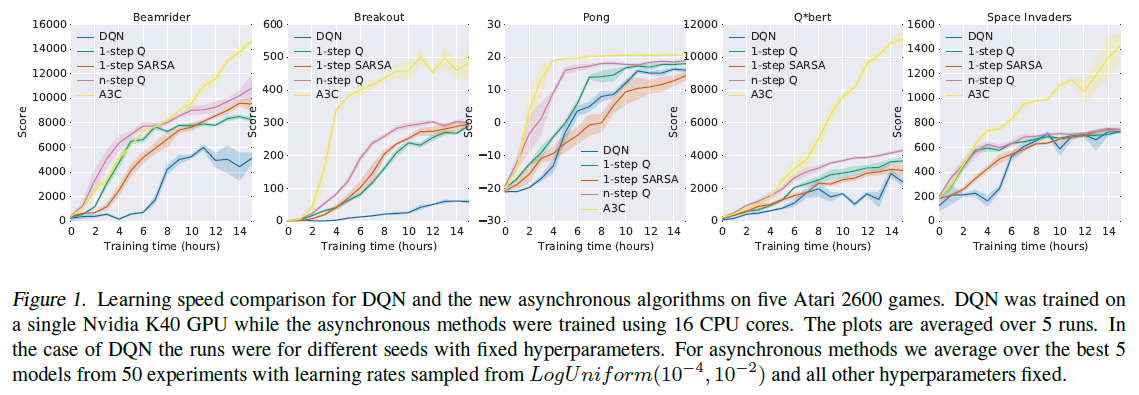
我们首先展示Atari 2600游戏子集的结果，以展示新方法的训练速度。图1比较了在Nvidia K40 GPU上训练的DQN算法的学习速度与在五款Atari 2600游戏上使用16个CPU核训练的异步方法的学习速度。结果表明，我们提出的所有四种异步方法都可以成功地在Atari域上训练神经网络控制器。异步方法的学习速度往往比DQN快，在某些游戏上学习速度明显更快，而仅在16个CPU内核上进行训练。此外，结果表明，在某些游戏中，n步方法比单步方法学习得更快。总体而言，基于策略的优势actor-critic方法明显优于所有三种基于价值的方法。
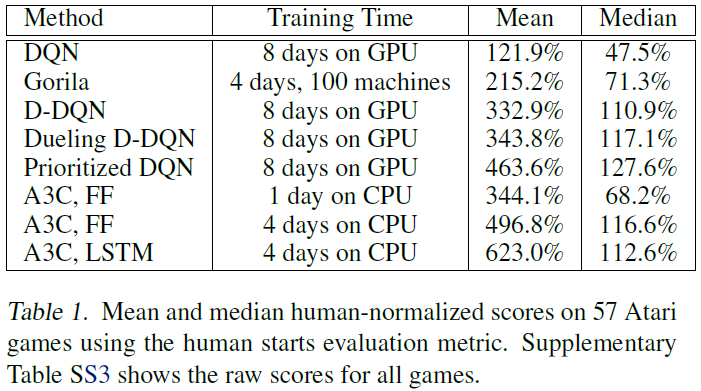
然后，我们评估了57款Atari游戏的异步优势actor-critic。为了与Atari游戏中的最新技术进行比较，我们在很大程度上遵循了(Van Hasselt et al., 2015)的训练和评估协议。具体来说，我们通过搜索六款Atari游戏(Beamrider、Breakout、Pong、Q*bert、Seaquest和Space Invaders)来调整超参数(学习率和梯度范数裁剪量)，然后固定所有57款游戏的所有超参数。我们训练了一个与(Mnih et al., 2015; Nair et al., 2015; Van Hasselt et al., 2015)具有相同架构的前馈智能体以及在最终隐藏层后具有额外256个LSTM单元的循环智能体。我们还使用最终的网络权重进行评估，以使结果与(Bellemare et al., 2012)的原始结果更具可比性。我们使用16个CPU核训练我们的智能体4天，而其他智能体在Nvidia K40 GPU上训练8到10天。表1显示了由我们的智能体通过异步优势actor-critic (A3C)以及当前最先进的技术训练获得的平均和中值人类标准化分数。补充表S3显示了所有游戏的得分。A3C在仅使用16个CPU核且不使用GPU的情况下，以其他方法的一半训练时间显著提高了57个比赛的平均得分。此外，仅经过一天的训练，A3C就与Dueling Double DQN的平均人类标准化得分相匹配，几乎达到了Gorila的人类标准化平均得分。我们注意到，Double DQN (Van Hasselt et al., 2015)和Dueling Double DQN (Wang et al., 2015)中提出的许多改进可以合并到这项工作中单步Q和n步Q方法具有类似的潜在改进。
5.2. TORCS Car Racing Simulator
我们还比较了TORCS 3D赛车游戏中的四种异步方法(Wymann et al., 2013)。TORCS不仅拥有比Atari 2600游戏更逼真的图形，而且还需要智能体学习它所控制的汽车的动力学。在每一步，智能体只接收到当前帧的RGB图像形式的视觉输入，以及与智能体在智能体当前位置沿轨道中心的速度成比例的奖励。我们使用了与补充第8节中指定的Atari实验中使用的相同的神经网络架构。我们使用四种不同的设置进行了实验——智能体控制有和没有对手机器人的慢车，以及智能体控制有和没有对手机器人的快车。完整结果可以在补充图S6中找到。A3C是性能最好的智能体，在大约12小时的训练中，达到了人类测试人员在所有四种游戏配置上获得的分数的大约75%到90%之间。可以在https://youtu.be/0xo1Ldx3L5Q找到显示A3C智能体的学习驾驶行为的视频。
5.3. Continuous Action Control Using the MuJoCo Physics Simulator
5.4. Labyrinth
我们在名为Labyrinth的新3D环境中使用A3C进行了一组额外的实验。我们考虑的具体任务涉及智能体学习在随机生成的迷宫中寻找奖励。在每一个回合开始时，智能体被放置在一个由房间和走廊组成的新随机生成的迷宫中。每个迷宫都包含两种类型的对象，智能体因发现而获得奖励——苹果和门户。捡起一个苹果会获得1的奖励。进入传送门会获得10的奖励，之后智能体会在迷宫中的一个新的随机位置重生，并且所有之前收集的苹果都会重新生成。一个回合在60秒后终止，之后将开始新的一个回合。智能体的目标是在时间限制内收集尽可能多的点，最佳策略包括首先找到门户，然后在每次重生后反复返回。这项任务比TORCS驾驶领域更具挑战性，因为智能体在每一个回合中都面临一个新的迷宫，并且必须学习探索随机迷宫的一般策略。
我们仅使用84 × 84 RGB图像作为输入，在此任务上训练了A3C LSTM智能体。大约50的最终平均分数表明智能体学到了一种合理的策略，仅使用视觉输入来探索随机3D最大值。https://youtu.be/nMR5mjCFZCw中包含了一段视频，展示了其中一个智能体探索以前看不见的迷宫。
5.5. Scalability and Data Efficiency
5.6. Robustness and Stability
6. Conclusions and Discussion
我们展示了四种标准强化学习算法的异步版本，并表明它们能够以稳定的方式在各种域上训练神经网络控制器。我们的结果表明，在我们提出的框架中，通过强化学习对神经网络进行稳定训练是可能的，无论是基于价值的方法还是基于策略的方法、异策和同策方法，以及离散域和连续域。当使用16个CPU核在Atari域上进行训练时，所提出的异步算法的训练速度比在Nvidia K40 GPU上训练的DQN更快，A3C在一半的训练时间内超过了当前最先进的算法。
我们的主要发现之一是，使用并行actor学习者更新共享模型对我们考虑的三种基于价值的方法的学习过程具有稳定作用。虽然这表明稳定的在线Q-learning在没有经验回放的情况下是可能的，这在DQN中用于此目的，但这并不意味着经验回放没有用处。将经验回放纳入异步强化学习框架可以通过重用旧数据来显著提高这些方法的数据效率。这反过来可能会导致在TORCS等领域中更快的训练时间，在这些领域与环境交互比为我们使用的架构更新模型更昂贵。
将其他现有的强化学习方法或深度强化学习的最新进展与我们的异步框架相结合，为立即改进我们提出的方法提供了许多可能性。虽然我们的n步方法在前向视图中运行(Sutton & Barto, 1998)，直接使用校正后的n步回报作为目标，但更常见的是使用后向视图通过资格迹隐式组合不同的回报(Watkins, 1989; Sutton & Barto, 1998; Peng & Williams, 1996)。通过使用其他估计优势函数的方法，例如(Schulman et al., 2015b)的广义优势估计，可以潜在地改进异步优势actor-critic方法。我们研究的所有基于价值的方法都可以从减少Q值高估偏差的不同方法中受益(Van Hasselt et al., 2015; Bellemare et al., 2016)。另一个更具推测性的方向是尝试将最近关于真正在线时序差分方法的工作(van Seijen et al., 2015)与非线性函数近似结合起来。
除了这些算法改进之外，还可以对神经网络架构进行一些补充改进。(Wang et al., 2015)的对偶架构已被证明可以通过为网络中的状态价值和优势包含单独的流来产生更准确的Q值估计。(Levine et al., 2015)提出的空间softmax可以通过使网络更容易表示特征坐标来改进基于价值和基于策略的方法。
