A Simple Neural Attentive Meta-Learner
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!
参考链接:https://blog.csdn.net/liuglen/article/details/84770069

ICLR 2018
时序卷积:https://blog.csdn.net/weixin_38498942/article/details/106824427
注意力机制:https://mp.weixin.qq.com/s/KKlmYOduXWqR74W03Kl-9A
Attention Is All You Need:https://zhuanlan.zhihu.com/p/51089880
ABSTRACT
深度神经网络在拥有大量数据的环境中表现出色,但在数据稀缺或需要快速适应任务变化时往往会遇到困难。作为回应,最近在元学习中的工作提出了对元学习器进行相似任务分布的训练,以期通过学习捕获(被要求解决的)问题本质的高层次策略,并将其泛化到新颖却相关的任务。但是,许多新的元学习方法都是经过大量手动设计的,或者使用专门用于特定应用的结构,或者使用硬编码算法组件来限制元学习器解决任务的方式。我们提出了一类简单且通用的元学习器架构,该架构使用时序卷积和软注意力的新颖组合。前者从过去的经验中收集信息,而后者则用于确定特定的信息。在迄今为止最广泛的元学习实验中,我们评估了一些基准测试任务所产生的简单神经注意力学习器(Simple Neural AttentIve Learning, SNAIL)。在监督学习和强化学习中的所有任务上,SNAIL都能获得最先进的性能。
1 INTRODUCTION
快速学习的能力是区分人类智力与人工智力的关键特征。人类有效地利用现有知识和经验来快速学习新技能。但是,当只有少量数据可用或需要适应不断变化的任务时,接受传统的监督学习或强化学习方法训练的人工学习器通常表现较差。
元学习旨在通过将学习器的范围扩大到相关任务的分布来解决这一缺陷。元学习器不是在单个任务上训练学习器(目标是从相似的数据分布中泛化出未见过的样本),而是在相似任务的分布中接受了训练,目标是学习一种从相似任务分布泛化到相关但未见过的任务的策略。传统上,成功的学习器会发现一个跨数据点进行泛化的规则,而成功的元学习器会学习一种对各个任务进行泛化的算法。
许多新近提出的元学习方法以在架构或算法级别上进行手工设计为代价,证明了性能的提高。在设计某些产品时已考虑到特定的应用,而其他一些产品已经内置了特定的高级策略。但是,对于任意范围的任务而言,最优策略对设计元学习器的人来说可能并不明显,在这种情况下,元学习器应具有灵活性,以学习解决提出的任务的最优方法。这样的元学习器将需要具有表达力,通用的模型架构,以便学习各种领域中的各种策略。
元学习可以形式化为序列到序列的问题。在采用这种观点的现有方法中,瓶颈在于元学习器内部化和参考过去经验的能力。因此,我们提出了一类解决此缺点的模型结构:我们结合了时序卷积,这使元学习器可以聚集过去经验中的上下文信息,并留有因果关系,从而可以在该上下文中查明特定信息。 我们在几个性能指标较高的元学习任务上评估了此简单神经学习器(SNAIL),包括监督学习中的Omniglot和mini-Imagenet数据集,以及强化学习中的多臂赌博机,表格式马尔可夫决策过程(MDP),视觉导航和连续控制。在所有领域中,SNAIL都能以相当可观的幅度实现最新性能,其性能优于特定于领域或依赖于内置算法的先验方法。
2 META-LEARNING PRELIMINARIES

3 A SIMPLE NEURAL ATTENTIVE LEARNER
激励我们采用这种方法的关键原则是简单性和多功能性:元学习器应该普遍适用于监督学习和强化学习中的各个领域。它应该足够通用且具有表达力,以学习最优策略,而不是已内置的策略。
Santoro et al. (2016)考虑了元学习问题的类似表述,并探索了使用RNN实现元学习器的方法。尽管简单且通用,但是它们的方法明显优于手工设计的用于利用领域或算法知识的方法(我们在第4节中研究的方法)。我们假设这是因为传统的RNN架构通过从一个时间步骤到另一个时间步骤将信息保持在隐含状态来传播信息。这种时间线性相关性限制了它们对输入流执行复杂计算的能力。
van den Oord et al. (2016a)引入了一类架构,这些架构通过在时间维度上执行一维膨胀卷积来生成序列数据(在他们的情况下为音频)。这些时序卷积(TC)是因果关系,因此下一时间步骤的生成值仅受过去时间步骤的影响,而不受未来时间步骤的影响。与传统的RNN相比,它们可以更直接且高带宽地访问过去的信息,从而使它们可以在固定大小的时间范围内执行更复杂的计算。但是,为了按比例缩放到长序列,膨胀速度通常会以指数方式增加,因此所需的层数将随序列长度按对数比例缩放。因此,它们可以更粗略地访问逆时序的输入。它们的有限能力和位置依赖性在元学习器中可能是不希望的,它应该能够充分利用越来越多的经验。
相比之下,软注意力(特别是Vaswani et al. (2017a)使用的样式)使模型可以从可能无限大的上下文中找出特定的信息。它将上下文视为无序的键-值存储,可以根据每个元素的内容进行查询。但是,缺乏位置依赖性也是不希望的,尤其是在强化学习中(观察,动作和奖励本质上是顺序的)。
尽管有各自的缺点,但时序卷积和注意力却是相辅相成的:前者以有限的上下文大小为代价提供了高带宽访问,而后者则在无限大的上下文中提供了精确的访问。因此,我们通过结合两者来构造SNAIL:我们使用时序卷积来产生使用因果注意操作的上下文。通过将TC层与因果注意层交织在一起,SNAIL可以在过去的经验范围内进行高带宽访问,而不会对其有效使用的经验量产生限制。通过在经过端到端训练的模型中的多个阶段使用注意力,SNAIL可以从所收集的经验中学习哪些信息可供选择,以及可以轻松完成特征表示。另一个好处是,SNAIL结构比传统的RNN(例如LSTM或GRU)(由于时间线性隐含状态依赖性而难以进行基础优化)更易于训练,并且可以有效地实现,从而可以在一次前向通过内处理整个序列。图1提供了SNAIL的图示,我们将在3.1节中讨论结构组件。
在有监督的设置中,SNAIL接收示例-标签对的序列(x1, y1), ... , (xt-1, yt-1)作为时间步骤1, ... , t−1的输入,后跟一个无标签的示例(xt, −)。然后,它根据先前见过的有标签示例输出对xt的预测。
在强化学习设置中,它接收一系列观察-动作-奖励元组(o1, -, -), ... , (ot, at-1, rt-1)。在每个时间 t,它根据当前观察值ot以及先前的观察值,动作和奖励输出动作at的分布。至关重要的是,遵循元RL中现有的工作(Duan et al., 2016; Wang et al., 2016),我们保留了跨回合边界的SNAIL的内部状态,从而使其具有跨越多个回合的记忆。观测值还包含指示回合终止的二值输入。

3.1 MODULAR BUILDING BLOCKS
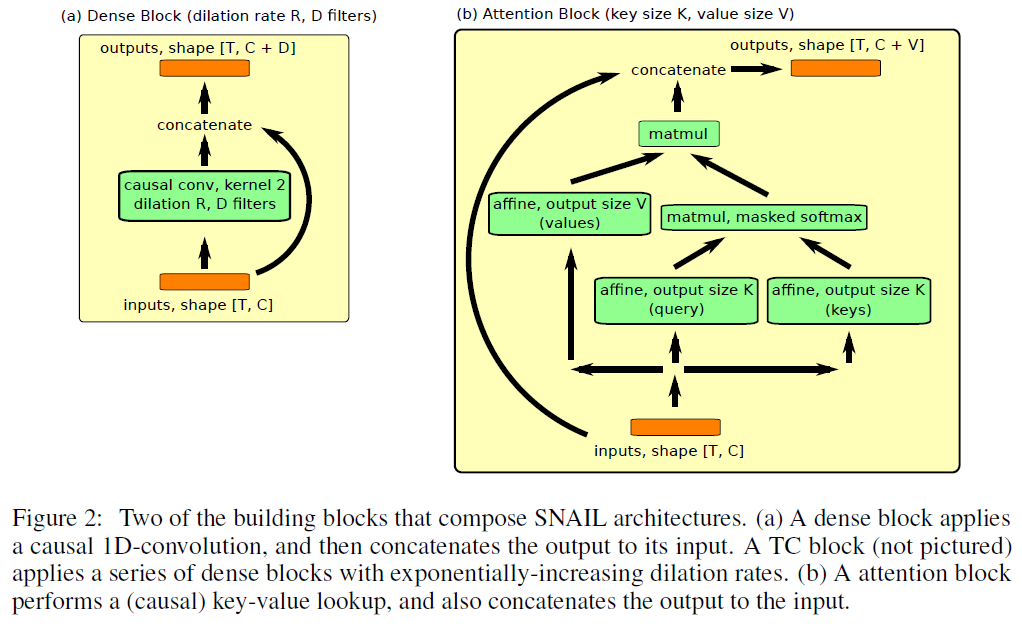
我们使用一些主要的构建块来构成SNAIL结构。下面,我们提供用于将每个块应用于大小为(序列长度)×(输入维数)的矩阵(伪代码中的"输入")的伪代码。值得注意的是,如果输入是图像,我们将使用一个额外的(空间)卷积网络,在将图像传递到SNAIL之前将其转换为特征向量。图2直观地显示了不同的块。
已经提出了许多技术来增加深度卷积架构的容量或加快其训练速度,包括批归一化(Ioffe&Szegedy (2015)),残差连接(He et al. (2016))和密集连接(Huang et al. (2016))。我们发现这些技术极大地提高了SNAIL的表达能力和训练速度,但是对于良好的性能,没有必要特别选择残差/密集配置(我们在附录B中探讨了SNAIL对结构选择的鲁棒性)。
密集块使用具有膨胀率R和滤波器数量D的单独因果一维卷积(我们在所有实验中均使用大小为2的核),然后将结果与其输入拼接起来。我们使用了由van den Oord et al. (2016a; b)引入的门控激活函数(第3行)。

TC块由一系列密集块组成,这些密集块的膨胀率呈指数增长,直到它们的感受野超过所需序列长度为止:

注意块执行单个键-值查找;我们根据Vaswani et al. (2017a)提出的自注意机制对这种操作进行样式设置:

其中CausallyMaskedSoftmax(·)在归一化之前将适当的概率归零,因此特定时间步骤的查询无法访问将来的键/值。
4 RELATED WORK
由Schmidhuber (1987); Naik&Mammone (1992); Thrun&Pratt (1998)率先提出,元学习并不是一个新主意。性能和泛化性之间的权衡是最近许多元学习方法的关键。我们讨论了几种著名的方法,以及它们如何适合这种范例。
Graves et al. (2014)研究了使用RNN来解决算法任务。他们尝试了由LSTM实现的元学习器,但是他们的结果表明LSTM结构无法满足此类任务的需要。然后,他们设计了一种更复杂的RNN架构,其中LSTM控制器耦合到可以从其读取和写入的外存库,并证明这些内存增强神经网络(MANN)的性能要比LSTM更好。Santoro et al. (2016)评估了LSTM和MANN元学习器对小样本图像的分类,并证实了LSTM结构的不足。这些方法是通用的,但是MANN具有复杂的内存寻址架构,难以训练——它们仍然遭受与LSTM相同的时间线性隐含状态依赖性。
相应地,几种方法在专门的神经网络结构的小样本分类中表现出良好的性能。Koch (2015)使用了经过训练的孪生网络来预测两个图像是否属于同一类别。Vinyals et al. (2016)学习了一个嵌入函数,并在注意力核中使用余弦距离来判断图像的相似性。Snell et al. (2017)采用了与Vinyals et al. (2016)类似的方法(基于欧式距离度量)。这三种方法在分类的上下文中均能很好地工作,但不适用于其他领域,例如强化学习。它们之所以表现出色是因为它们的结构旨在利用领域知识,但是理想情况下,我们希望使用不局限于特定问题类型的元学习器。
许多方法考虑使用元学习器来更新传统学习器的参数(Bengio et al., 1992; Hochreiter et al., 2001)。Andrychowicz et al. (2016)和Li&Malik (2017)研究了学习优化的设置,其中学习器是最小化的目标函数,元学习器使用学习器的梯度来执行优化。他们的元学习器是由LSTM实现的,其学习的策略可以解释为基于梯度的优化算法。但是,尚不清楚学到的优化器是否比现有的基于SGD的方法好得多。
Ravi&Larochelle (2017)在小样本分类设置中使用类似的LSTM元学习器来扩展这个想法,其中传统的学习器是基于卷积网络的分类器。在这种情况下,元学习算法被分解为两部分:传统学习器的初始参数经过训练,适合基于梯度的快速自适应;LSTM元学习器被训练为适合元学习任务的优化算法。Finn et al. (2017)探索了一种特殊情况,其中元学习器被限制使用普通的梯度下降来更新学习者,并表明该简化模型(称为MAML)可以实现同等的性能。Munkhdalai&Yu (2017)探索了一种更复杂的权重更新方案,该方案在小样本分类上产生了较小的性能改进。
上一段中讨论的所有方法都具有域无关的好处,但是它们为元学习器明确地遵循了一种特定的策略(即在测试时通过梯度下降进行自适应)。在特定领域中,可能存在更好的策略来利用任务的结构,但是基于梯度的方法将无法发现它们。相比之下,SNAIL提出了一种替代范例,其中通用结构具有学习利用特定领域任务结构的算法的能力。
Duan et al. (2016)和Wang et al. (2016)都使用传统的RNN架构(GRU和LSTM)研究了强化学习领域的元学习。此外,Finn et al. (2017)尝试在连续控制中快速调整策略,其中对元学习器进行了与紧密相关的运动任务分布有关的训练。在5.2节中,我们将SNAIL与MAML和基于LSTM的元学习器相对比,以这些工作考虑的任务作为基准。
5 EXPERIMENTS
我们的实验旨在调查以下问题:
- SNAIL的泛化性如何影响其在一系列元学习任务中的性能?
- 它的性能是否能够与专门针对特定任务领域,或者已经内置了高层次策略的元素的现有方法相比?
- SNAIL如何在高维输入和长期时序依赖性方面进行缩放?
5.1 FEW-SHOT IMAGE CLASSIFICATION
在小样本分类设置中,当每个类别只有少量(K个)带标记的示例时,我们希望将数据点分为N个类别。元学习器很容易应用,因为它学习如何比较输入点,而不是记住从点到类的特定映射。
(省略)
5.2 REINFORCEMENT LEARNING
强化学习具有监督学习所没有的许多挑战,包括长期的时序依赖性(因为经历的状态和奖励可能取决于许多时间步骤之前采取的动作)以及探索和开发的平衡。为了探索SNAIL学习RL算法的能力,我们根据元RL1的先前工作在四个不同的领域对它进行了评估:
- 多臂赌博机(Duan et al., 2016; Wang et al., 2016):智能体与一组奖励分布未知的臂相互作用。尽管其动作不会影响其状态,但是探索和开发都是必不可少的:最优智能体必须首先通过对不同臂进行采样来进行探索,但随后通过反复选择最优臂来利用其知识。
- 表格式MDP(Duan et al., 2016; Wang et al., 2016):我们从程序上生成随机MDP,并允许智能体在多个回合中采取动作。由于每个MDP都不相同,因此元学习器不能简单地记住受过训练的MDP。它实际上必须学习一种解决MDP的算法。
- 视觉导航(Duan et al., 2016; Wang et al., 2016):智能体必须使用仅视觉观测作为输入,才能导航随机生成的迷宫以找到随机定位的目标。允许它与相同的迷宫/目标配置交互两个回合,因此,最优智能体应在第一个回合中探索迷宫以找到目标,然后在第二个回合中直接进入目标。该任务的特点是深度RL中的许多常见挑战,包括高维观测,部分可观察性和稀疏奖励。
- 连续控制(Finn et al., 2017):我们考虑了一组仿真运动任务。尽管环境动态很复杂,但是潜在的任务分布却非常狭窄。作为结果,元学习器需要利用大量的任务结构。最优策略比真正的RL算法更接近任务识别。
在这些领域中,我们都训练了SNAIL以及两个元学习基准:
- 基于LSTM的元学习器,由Duan et al. (2016); Wang et al. (2016)同时提出。在后续章节的表和图中,我们将此方法称为"LSTM"。
- MAML,由Finn et al. (2017)引入的方法。它训练策略的初始参数,以在对新任务进行一次(策略)梯度更新后实现最优性能。
我们还进行了一些消融实验,这些实验在附录D中进行了详细说明。
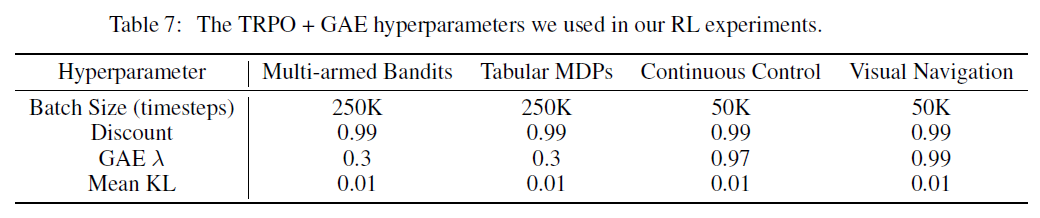
在所有领域中,我们使用具有广义优势估计的信任域策略优化来训练元学习器(使用GAE的TRPO; Schulman et al. (2015; 2016));附录C详细介绍了SNAIL结构和TRPO/GAE超参数。
在赌博机和MDP领域中,存在许多具有各种最优性保证的人工设计算法(我们将在随后的部分中进行更深入的讨论)。尽管元学习器没有太多的任务结构可以利用,但是渐近性能上限的存在让我们评估了元学习算法的最优性。
但是,元学习器的真正用途是它可以学习专门针对其所训练任务的特定分布的算法。我们在视觉导航和连续控制领域对此进行评估,在这些领域中,元学习器可以利用重要的任务结构,但是由于任务复杂性,没有最优算法可知。
1 一些视频结果可在https://sites.google.com/view/snail-iclr-2018/中找到。
5.2.1 MULTI-ARMED BANDITS
在我们的赌博机实验中(按照Duan et al. (2016)的风格进行),K臂中的每一个根据Bernoulli分布给予奖励,Bernoulli分布的参数p ∈ [0, 1]在每个长度为N的回合开始时随机选择。每个时间步骤,元学习器都会收到前一个时间步骤的奖励,以及所选对应臂的one-hot编码。它在K臂上输出离散的概率分布;通过从该分布中采样确定选定的臂。
作为oracle,我们考虑了Gittins指数(Gittins, 1979),这是折扣无穷时间步骤设置中的贝叶斯最优解。因为只有N → ∞时这才是最优的,元学习器可以通过选择更早地开发而在较小的N方面胜过它。
继Duan et al. (2016),我们测试了N = 10, 100, 500和K = 5, 10, 50的所有组合。我们还测试了N = 1000, K = 50的额外情况,以进一步评估SNAIL对更长序列的可拓展性。我们报告每种设置的每回合平均奖励;结果在表3中给出,可用置信区间为95%。我们发现,对于N = 500, 1000,训练MAML在计算上过于昂贵。因此,我们忽略了表3中的结果。
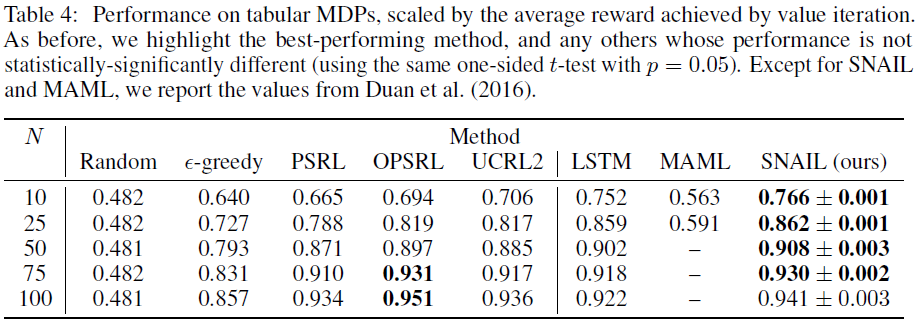
5.2.2 TABULAR MDPS
在我们的表格式MDP实验中(同样遵循Duan et al., 2016)),每个MDP具有10个状态和5个动作(均是离散的);每个(状态,动作)对的奖励遵循具有单位方差的正态分布,其中均值是从N(1, 1)采样的,而转换是从带有随机参数的平坦Dirichlet分布采样的(后者是在贝叶斯RL中常用的先验)。我们允许每个元学习器与MDP进行N个长度为10的回合的交互。作为输入,他们收到了当前状态和先前动作的one-hot编码,先前收到的奖励以及指示当前回合终止的二值标志。
除随机智能体外,我们还将以下人工设计的算法视为基准。
- PSRL (Strens, 2000):一种贝叶斯方法,用于估计当前MDP参数的信度。在N个回合中的每个回合的开始处,它将从当前后验中采样一个MDP,并根据回合其余部分的最优策略采取动作。
- OPSRL (Osband & Van Roy, 2017):PSRL的乐观变体。
- UCRL2 (Jaksch et al., 2010):使用扩展价值迭代过程来计算当前信度下的乐观MDP。
- ε-贪婪:以1−ε的概率,根据当前后验(每回合更新一次)针对MAP估计采取最优动作。
作为oracle,我们在每个MDP上运行价值迭代10次(回合长度)。当已知MDP参数(奖励函数,转换概率)时,价值迭代是最优的;因此,结果价值为任何算法的性能提供了上限,无论是人工设计的还是元学习到的(不接收MDP参数)。
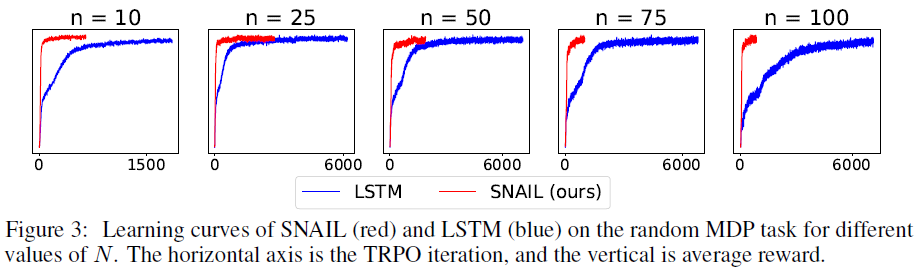
我们测试了N = 10, 25, 50, 75, 100;在表4中,我们报告了由价值迭代上限归一化的性能。随着N的增加,性能应接近1,因为该算法可了解有关当前MDP的更多信息。与赌博机实验相似,在N = 50, 75, 100的情况下,我们无法成功训练MAML。在图3中,我们显示了SNAIL和LSTM的学习曲线。
5.2.3 CONTINUOUS CONTROL
我们考虑Finn et al. (2017)引入的一组任务,其中两个模拟机器人(planar cheetah和3D-quadruped ant)必须沿特定方向或以指定速度运行(方向或速度是随机选择的,而不告诉智能体)。在目标方向实验中,奖励是机器人在向前或向后方向上速度的大小,而在目标速度实验中,奖励是机器人当前向前速度与目标之间的负绝对值。观察值是机器人的关节角度和速度,而动作是机器人的关节扭矩。对于这四个任务分布({ant, cheetah} × {goal velocity, target direction}),Finn et al. (2017)对新采样的任务使用20个回合(蚂蚁为40)(每个回合为200个时间步骤)更新了一个策略梯度后,训练了一个策略以使其性能最大化。
我们针对这四个任务类别分别训练了SNAIL和LSTM。由于它们不会在测试时更新参数(而是通过隐含状态吸收经验),因此SNAIL和LSTM除了当前的观察值之外,还会接收到先前的动作,先前的奖励以及回合终止标志作为输入。我们发现,两回合的交互足以使这些元学习器适应任务,并且将它们展开更长的时间并不能改进性能。
在图4中,我们显示了不同的方法如何适应新任务。作为oracle,我们从每个分布中采样任务,并为每个任务训练了一个单独的策略。我们将每个任务分布的oracle策略的平均性能绘制为元学习器性能的上限。
定性地,我们可以将MAML视为将通用策略(即梯度下降)应用于高度结构化任务的分布。相比之下,SNAIL和LSTM能够基于共享的任务结构来对自己进行专门化,从而使它们能够在第一个回合的初始时间步骤内识别任务,然后以最优方式采取动作。
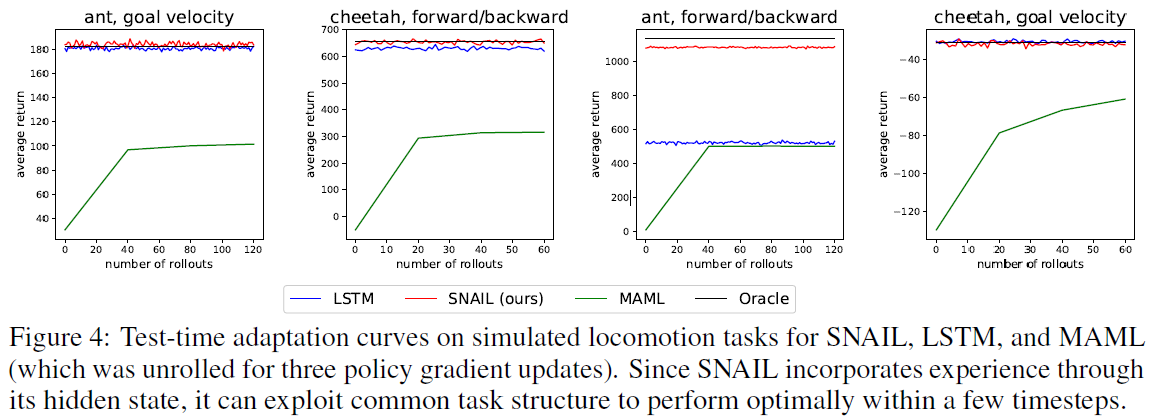
5.2.4 VISUAL NAVIGATION
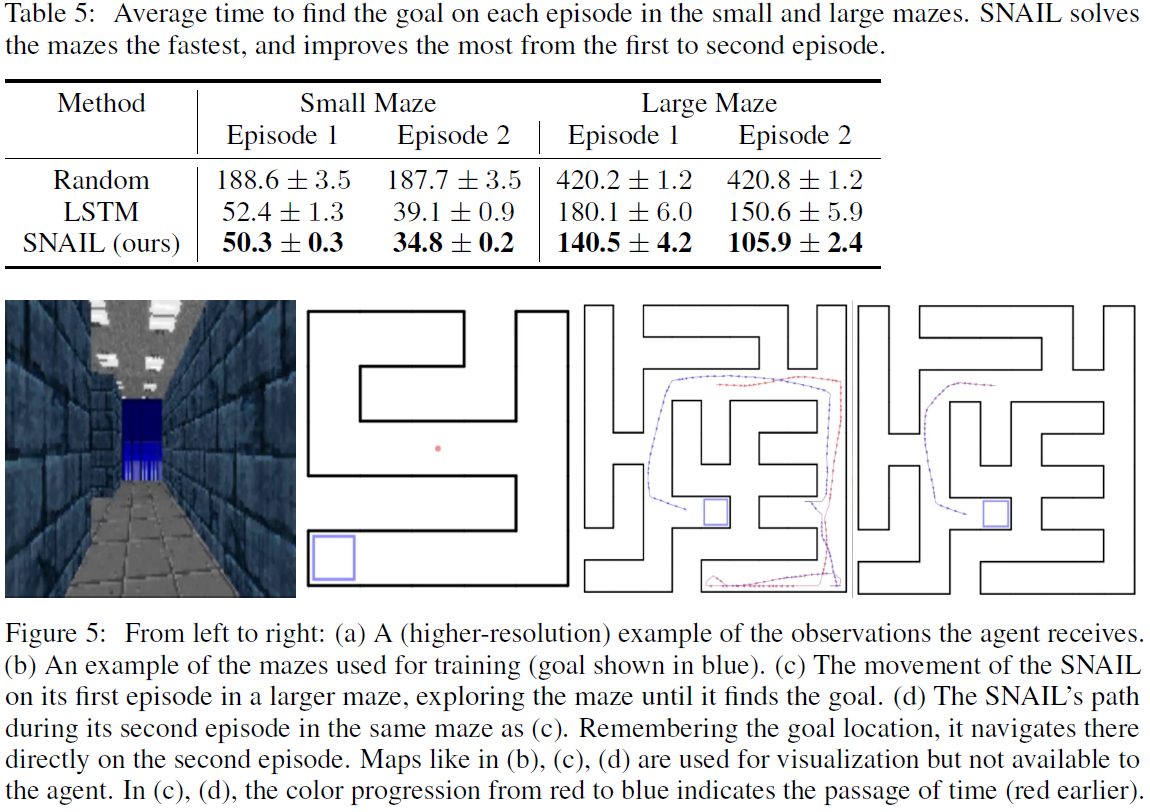
Duan et al. (2016)和Wang et al. (2016)都考虑了视觉导航的任务,其中智能体必须仅使用视觉输入在迷宫中找到目标。前者使用随机生成的迷宫和目标位置,而后者使用固定的迷宫和仅四个不同的目标位置。因此,我们在前一项更具挑战性的任务上评估了SNAIL。智能体收到的观察值是30×40的第一人称图像,并且可以执行的动作是{前进,向左微调,向右微调}。我们构建了一个训练数据集和两个测试数据集(分别具有相同和更大的未见过的迷宫),每个都有1000个迷宫。允许智能体与每个迷宫交互2个回合,其回合时长为250(在较大的迷宫中为1000)。每个试验都随机选择起点和目标位置,但在每对回合中均保持固定。智能体到达目标时会得到+1的奖励(这导致回合终止),在每个时间步骤处获得-0.01的奖励,以鼓励目标更快地达到目标,而撞墙会获得-0.001的奖励。图5描绘了观测值以及迷宫布局的示例。
我们使用平均回合长度对每种方法进行评估(试验中的第一个和第二个回合)。结果显示在表5中。由于MAML在赌博机和MDP域中无法按比例缩放到长序列,因此我们没有在该域上对其进行评估;计算代价过高。定性地,我们观察到确实存在最优策略:SNAIL智能体在第一个回合中探索迷宫,然后在找到目标后直接在第二个回合去迷宫(LSTM智能体也表现出这种行为,但很难记住目标在哪里)。图5给出了一个图示。
6 CONCLUSION AND FUTURE WORK
我们提出了一种简单且通用的元学习结构,其动机是需要元学习器快速整合并参考过去的经验。我们的简单神经注意力学习器(SNAIL)利用时序卷积和因果注意力的新颖组合,这是具有优劣互补的序列到序列模型的两个构建块。我们证明SNAIL在监督学习和强化学习中,在所有最广泛基准的元学习任务上均取得了可观的进步,而无需依赖任何特定于应用的结构组件或算法先验。
尽管我们在设计SNAIL时考虑到元学习,但它可能在其他序列到序列任务(例如语言建模或翻译)方面表现出色。我们计划在以后的工作中对此进行探索。
另一个有趣的想法是训练一个可以在其经验的整个生命周期中注意的元学习器(而不是像本工作中那样,仅注意一些近期回合)。具有这种终生记忆的智能体可以更快地学习并更好地泛化。但是,为了使计算要求切实可行,还需要学习如何确定值得记住的经验。
APPENDIX
A FEW-SHOT CLASSIFICATION ARCHITECTURES
B FEW-SHOT CLASSIFICATION: ABLATIONS
C REINFORCEMENT LEARNING
C.1 MULTI-ARMED BANDIT AND TABULAR MDP ARCHITECTURES
对于N个时间步骤,K臂赌博机问题,总轨迹长度为T = N。对于每个MDP有N个回合的MDP问题,它是T = 10N (因为每个回合持续10个时间步骤)。
对于多臂赌博机和表格式MDP,我们使用了相同的结构。首先,我们应用了具有32个输出的全连接层,该层在策略和价值函数之间共享。然后使用该策略:TCBlock(T, 32), TCBlock(T, 32), AttentionBlock(32, 32)。使用的价值函数:TCBlock(T, 16), TCBlock(T, 16), AttentionBlock(16, 16)。
我们发现,删除注意块不会对赌博机问题产生任何影响,而没有注意的SNAIL则无法学会解决MDP。
C.2 CONTINUOUS CONTROL ARCHITECTURES
对于每个仿真运动任务,总轨迹长度为T = 400 (2个回合,每个回合有200个时间步骤)。我们对所有任务使用相同的架构(在策略和价值函数之间共享):两个具有tanh非线性的大小为256的全连接层,AttentionBlock(32, 32), TCBlock(T, 16), TCBlock(T, 16), AttentionBlock(32, 32)。然后,策略和价值函数应用单独的全连接层以产生必需的输出维数。
C.3 VISUAL NAVIGATION ARCHITECTURES
与我们考虑过的其他RL任务不同,该域中的观察值包括图像。我们使用与Duan et al. (2016)相同的卷积架构对图像进行预处理:两层{核大小为5×5,有16个滤波器,步长为2,ReLU非线性},然后将其输出扁平化,然后传递到全连接层以生成大小为256的特征向量。
总轨迹长度为T = 500 (2个回合,每个回合有250个时间步骤)。对于该策略,我们使用了:TCBlock(T, 32), AttentionBlock(16, 16), TCBlock(T, 32), AttentionBlock(16, 16)。对于价值函数,我们使用了:TCBlock(T, 16), TCBlock(T, 16)。
C.4 ADDITIONAL REINFORCEMENT LEARNING HYPERPARAMETERS
正如在5.2节中讨论的那样,我们使用了带有广义优势估计的信任域策略优化来训练所有策略(TRPO with GAE, Schulman et al. (2015; 2016))。表7中列出了超参数。对于多臂赌博机,表格式MDP和视觉导航,我们使用了与Duan et al. (2016)相同的超参数,使我们的结果可直接比较;额外调整可能会改进SNAIL的性能。
D REINFORCEMENT LEARNING: ABLATIONS
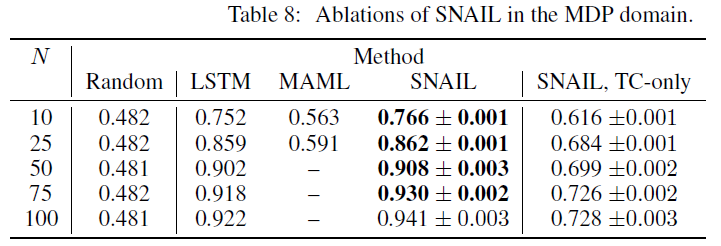
在这里,我们对RL任务进行一些消融实验:我们将在5.2节中探索仅依靠TC层还是仅依靠注意层的智能体可以解决多臂赌博机或MDP任务。
首先,我们考虑一个没有注意层的SNAIL智能体(只有TC层,相当于van den Oord et al. (2016a)引入的WaveNet架构的变体)。
当将其应用于赌博机领域时,我们发现此仅TC模型与完整的SNAIL一样出色。这可能是由于此任务域的简单性,因为成功解决赌博机问题并不需要保留大量的过去经验。实际上,许多人为设计的算法(包括渐近最优的Gittins指数)仅在每个时间步骤更新运行统计信息。
但是,该模型在需要更复杂算法的MDP域中苦苦挣扎。结果在下表中(与随机智能体,SNAIL,LSTM和MAML的结果重复自表4,以供参考)。该智能体的渐近次优性表明,其将过去的经验内部化的能力已达到饱和。
接下来,我们考虑了没有TC层的SNAIL智能体(仅注意)。由于RL任务的序列性质,我们采用了Vaswani et al. (2017b)提出的位置编码。该模型等效于其Transformer结构,无法解决赌博机或MDP任务。在这两个领域中,它的性能都不比随机好。无济于事,我们尝试了多个注意力块,每个块有多个头部。
我们假设这种结构的不足之处是由于单纯的细心查找无法轻松处理序列信息这一事实。尽管它们具有无限的感受野,但它们无法以与单个卷积相同的方式直接比较两个相邻的时间步骤(例如,单个状态-动作-状态转换)。TC层是必不可少的,因为它们允许智能体局部分析序列的连续部分,以产生更好的上下文表征。