Improving Generalization in Meta Reinforcement Learning using Learned Objectives

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

Published as a conference paper at ICLR 2020

 

论文作者博客：http://louiskirsch.com/metagenrl

 

ABSTRACT

　　生物进化将许多学习者的经验提炼为人类的通用学习算法。我们新颖的元强化学习算法MetaGenRL受此过程启发。MetaGenRL提取了许多复杂智能体的经验，以元学习一种低复杂度的神经目标函数，该函数决定了未来单独的学习方式。与最近的meta-RL算法不同，MetaGenRL可以推广到与元训练完全不同的新环境。在某些情况下，它甚至优于人工设计的RL算法。MetaGenRL在元训练期间使用异策二阶梯度，可大大提高其采样效率。

 

1 INTRODUCTION

　　进化的过程为人类提供了难以置信的通用学习算法。它们使我们能够解决各种各样的问题，即使没有大量相关的先前经验也是如此。产生这些功能的算法是在自然进化过程中提炼许多学习者的集体经验的结果。通过本质上以这种方式从学习经验中学习，可以将所得知识紧凑地编码在单独的遗传密码中，从而产生我们今天观察到的通用学习能力。

　　相反，人工智能体中的RL很少以这种方式进行。用于训练智能体的学习规则是人类工程和设计多年的结果(例如，Williams (1992); Wierstra et al. (2008); Mnih et al. (2013); Lillicrap et al. (2016); Schulman et al. (2015a))。相应地，人工智能体固有地受到设计者结合正确的归纳偏差以便从以前的经验中学习的能力的限制。

　　一些工作提出了基于元RL的替代框架(Schmidhuber, 1994; Wang et al., 2016; Duan et al., 2016; Finn et al., 2017; Houthooft et al., 2018; Clune, 2019)。Meta-RL区分了在环境中学会动作(RL问题)和学会学习(元学习问题)。因此，现在学习本身是一个学习问题，从原则上讲，它使人们可以利用先前的学习经验来元学习通用的学习规则，而这些规则将超过人工设计的替代方法。然而，尽管先前的工作发现可以通过元学习将学习规则推广到略有不同的环境或目标(Finn et al., 2017; Plppert et al., 2018; Houthooft et al., 2018)，但推广到完全不同的环境仍然是一个悬而未决的问题。

　　在本文中，我们介绍了MetaGenRL¹，这是一种新颖的元强化学习算法，该算法可以学会可推广到完全不同环境的学习规则。MetaGenRL受到自然进化过程的启发，将许多智能体的经验提炼成目标函数的参数，该函数决定了未来单独的学习方式。与进化策略梯度(EPG; Houthooft et al. (2018))类似，它元学习低复杂度的神经目标函数，可用于训练具有许多参数的复杂智能体。但是，与EPG不同，它能够使用二阶梯度进行元学习，这将提供一些优势，正如我们将要演示的那样。

　　我们评估了MetaGenRL在各种连续控制任务上的性能，并与RL²(Wang et al., 2016; Duan et al., 2016)和EPG进行了比较，此外还采用了几种人工设计的学习算法。

　　与RL²相比，我们发现MetaGenRL不会过拟合，并且能够在完全不同的环境中使用元学习的学习规则来训练随机初始化的智能体。与EPG相比，我们发现MetaGenRL的采样效率更高，并且在固定的环境交互预算下的性能明显优于其他。消融研究和其他分析的结果可进一步了解我们方法的益处。

 

¹ 代码可以在http://louiskirsch.com/code/metagenrl中获取

 

2 PRELIMINARIES

 

Human Engineered Gradient Estimators 最大化等式1的一种流行的基于梯度的方法是REINFORCE (Williams, 1992)。就使用似然比技巧来导出下面形式的梯度估计而言，它直接将等式1进行微分：

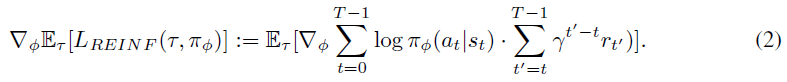
　　尽管这种基本估计量在实践中很少使用，但已成为这种形式的整个策略梯度算法类的基础。例如，Schulman et al. (2015b)的热门扩展将REINFORCE与广义优势估计(GAE)相结合，得出以下策略梯度估计量：

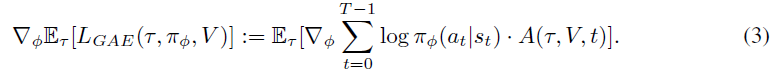
其中A(τ, V, t)是GAE且V : S → R是价值函数估计。最近的其他一些扩展包括TRPO (Schulman et al., 2015a)，它通过使用信任区域和迭代的异策更新来阻止不良的策略更新，或者PPO (Schulman et al., 2017)，它仅使用一阶近似就可以提供类似的好处。

 

Parametrized Objective Functions 在这项工作中，我们注意到许多这些人为设计的策略梯度估计量可以看作是通用目标函数L的特定实现，该目标函数相对于策略参数微分：

　　因此，考虑对参数α的各种选择恢复其中一些估计量的L的通用参数化是很自然的。在本文中，我们将考虑通过神经网络实现L_α的神经目标函数。然后，我们的目标是优化此神经网络的参数α，以便产生一种新的学习算法，该算法可以在整个(不同)环境类别中最优地最大化等式1。

 

3 META-LEARNING NEURAL OBJECTIVES

　　在这项工作中，我们提出了MetaGenRL，这是一种新颖的元强化学习算法，该算法元学习形式为L_α(τ, π_Φ, V)的神经目标函数。MetaGenRL利用价值函数和二阶梯度，与以前的工作相比，其采样效率更高(Duan et al., 2016; Wang et al., 2016; Houthooft et al., 2018)。更重要的是，正如我们将演示的那样，MetaGenRL元学习目标函数可以推广到非常不同的环境。

　　我们的主要见解是可微的critic：Q_θ : S x A → R可用于基于相应策略梯度的质量来度量局部更改目标函数参数α的效果。通过与一组(可能不同的)环境进行交互，这使一组智能体可以使用和改进单个参数化的目标函数L_α。在评估(元测试时间)期间，可以将元学习的目标函数用于在新环境中训练随机初始化的RL智能体。

 

3.1 FROM DDPG TO GRADIENT-BASED META-LEARNING OF NEURAL OBJECTIVES

　　我们将正式引入MetaGenRL作为DDPG actor-critic框架的扩展(Silver et al., 2014; Lillicrap et al., 2016)。在DDPG中，形式为Q_θ : S x A → R的参数化critic将任何s_t ∈ S的不可微RL奖励最大化问题转化为短视价值最大化问题。这是通过在critic Q_θ的优化和(此处为确定性)策略π_Φ之间交替进行的。critic经过以下训练，以最小化TD误差：

并且y_t对参数向量θ的依赖性将被忽略。通过遵循梯度改进了策略π_Φ，以增加来自任意状态的期望回报。通过从回放缓存中采样轨迹，可以完全异策计算两个梯度。

　　MetaGenRL建立在微分critic Q_θ和策略参数的想法上。它合并了用于改进策略的参数化目标函数L_α(即通过遵循梯度)，这增加了一个额外的间接级别：critic Q改进了L_α，而L_α改进了策略π_Φ。通过首先微分目标函数参数α，然后微分策略参数Φ，critic可以用来评估使用L_α对估计回报进行π_Φ更新的效果²：

　　这构成了一种二阶梯度，可以用来对L_α进行元训练，以在将来对策略参数提供更好的更新。在实践中，我们将使用批处理在多个轨迹τ上优化等式6。

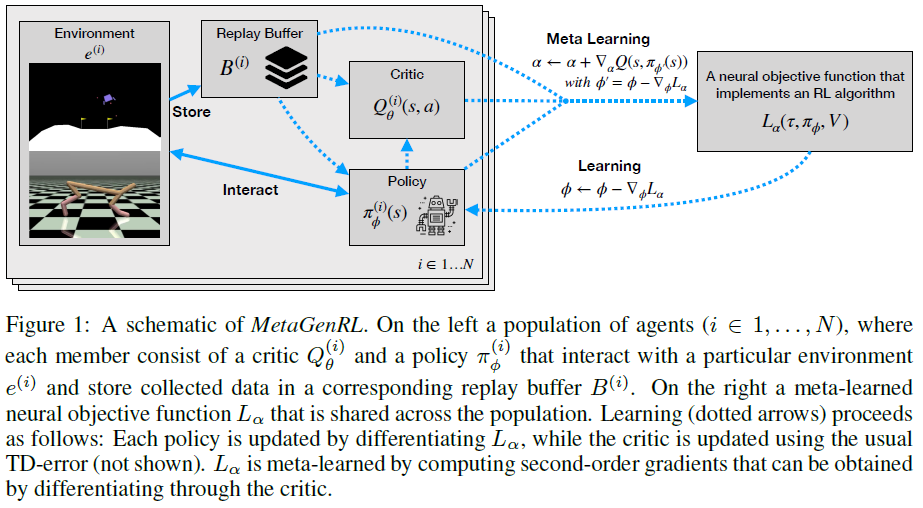
　　与第2节中的策略梯度估计量相似，目标函数L_α(τ, x(Φ), V)接收回合轨迹τ = (s_0:T-1; a_0:T-1; r_0:T-1)作为输入，价值函数估计V和辅助输入x(Φ)(以前是π_Φ)，可以根据策略参数进行微分。后者对于能够对Φ进行微分至关重要，在最简单的情况下，这包括策略所预测的动作。虽然等式6用于元学习L_α，但目标函数L_α本身用于遵循的策略学习。概述见图1。MetaGenRL包含两个阶段：在元训练期间，我们在critic更新，目标函数更新和策略更新之间交替，以元学习算法1中所述的目标函数L_α。在算法2的元测试中，我们采用了学到的目标函数L_α并保持不变，同时在新环境中训练随机初始化的策略以评估其性能。

　　我们注意到，L_α的输入是从回放缓存中采样的，而不是仅使用同策数据。如果L_α代表REINFORCE类型的目标，则意味着微分L_α会产生有偏的策略梯度估计。在我们的实验中，我们将发现，与有偏的异策REINFORCE算法和重要性采样的无偏REINFORCE算法相比，L_α的梯度要好得多，同时还改进了流行的同策REINFORCE和PPO算法。

² 在采用概率策略π_Φ(a_t|s_t)的情况下，以下内容成为π_Φ的期望，并且需要可重新参数化的形式。在这里，我们专注于学习确定性目标策略。

 

3.2 PARAMETRIZING THE OBJECTIVE FUNCTION

　　我们将使用LSTM (Gers et al., 2000; Hochreiter＆Schmidhuber, 1997)来实现L_α，该LSTM以相反的顺序进行τ迭代，并取决于当前的策略动作π_Φ(s_t)(见图2)。在每个时间步骤，L_α会收到奖励r_t，采取的动作a_t，当前策略π_Φ(s_t)的预测动作，时间 t 和价值函数估计V_t, V_t+1³。在每个步骤中，LSTM输出目标价值l_t，将所有目标价值相加以得出可以相对于Φ进行微分的单个标量输出价值。为了适应不同环境中变化的动作维度，首先对π_Φ(s_t)和a_t进行卷积，然后求平均值，以获得不依赖于动作维度的动作嵌入。附录B中提供了其他详细信息，包括对更具表现力的替代方案的建议。

　　通过以相反的顺序向LSTM(相应地和L_α)显示轨迹，类似于策略梯度估计量，它可以根据动作a_t对奖励的未来影响将责任分配给该动作。更重要的是，作为使用这些输入的通用函数近似，LSTM原则上可以学习类似于优势估计，广义优势估计或重要性权重⁴的不同方差和偏差减少技术。由于这些特性，我们希望所支持的目标函数类别与使用广义优势估计(Schulman et al., 2015b)的REINFORCE估计器(Williams, 1992)有关。

 

³ 价值估计是从Q函数得出的，即V_t = Q_θ(s_t, π_Φ(s_t))，并被视为常量输入。因此，梯度不能向后流过Q_θ，这确保了L_α不能天真地学会实现类似DDPG的目标函数。

⁴ 我们注意到，在实践中很难评估元学习目标函数是否包含了偏差/方差减少技术，尤其是因为MetaGenRL不太可能恢复已知技术。

 

3.3 GENERALITY AND EFFICIENCY OF METAGENRL

　　MetaGenRL为元学习目标函数提供了一个通用框架，该框架可以表示各种学习算法。特别是，对于策略参数Φ，只要求π_Φ和L_α都可以微分。在当前的工作中，我们利用这种灵活性来利用基于群体的元优化，通过异策二阶梯度来提高样本效率，并提高元学习目标函数的泛化能力。

 

Population-Based 通用目标函数应适用于广泛的环境和智能体参数。在此程度上，MetaGenRL能够通过使用在一组智能体中共享的单个目标函数L_α来利用多个智能体的集体经验来执行元学习，每个智能体在各自(可能不同)的环境中起作用。每个智能体在一批轨迹上局部计算等式6，然后将所得的梯度合并以更新L_α。因此，每个单独智能体的相关学习经验被压缩为在任何给定时间可供整个群体使用的目标函数。

 

Sample Efficiency 使用智能体群体来学习神经目标函数的另一种方法是通过EPG中的进化(Houthooft et al., 2018)。但是，我们希望像MetaGenRL一样，使用二阶梯度进行元学习会大大提高采样效率。这是由于对目标函数L_α进行了异策训练，以及其随后使用异策改进策略。确实，与进化过程不同，无需整体训练多个随机初始化的智能体程序即可评估目标函数，从而加快了责任分配的速度。相反，在任何时间点，任何对未来环境交互有用的信息都可以直接合并到目标函数中。最后，使用公式6中的式子，可以通过在应用Q_θ之前增加相应的梯度步骤来测量使用L_α进行多步改进策略的效果，这将在5.2.3节中进行探讨。

 

Meta-Generalization 这项工作的重点是学习通用的学习规则，这些规则可以在测试期间应用于极为不同的环境。策略与学习规则，后者的函数形式以及跨许多环境的训练之间的严格分离都有助于实现这一目标。关于前者，由于两个原因，如MetaGenRL中所述，将策略与学习规则明确分开是有利的。首先，它允许我们指定学习规则的参数数量，而与策略和critic参数无关。例如，我们的L_α实现仅将15K参数用于目标函数，而将384K参数用于策略和critic。因此，我们只能为学习规则使用简短的描述长度。获得的第二个优点是元学习器无法直接更改策略，因此必须学习使用目标函数。这使得元学习器很难过拟合于训练环境。

 

4 RELATED WORK

　　在元学习中，最早的追求是遗传算法的元层次结构(Schmidhuber, 1987)和监督学习中的学习更新规则(Bengio et al., 1990)。前者介绍了整个元层次结构的通用框架，但它依赖于离散的不可微程序。后者引入了包括自由参数的局部更新规则，可以在监督设置中使用梯度来学习这些规则。Schmidhuber (1993)引入了一种可微的自引用RNN，尽管难以学习，但它可以解决和修改其自身的权重。

　　Hochreiter et al. (2001)介绍了使用RNN进行可微的元学习，以扩展到更大的问题实例。通过给RNN访问其预测误差，它可以实现自己的元学习算法，其中权重是元学习的参数，而隐含状态则是学习的主题。随后将其扩展到RL设置(Wang et al., 2016; Duan et al., 2016; Santoro et al., 2016; Mishra et al., 2018)(此处称为RL²)。正如我们在论文中凭经验显示的那样，使用RL²进行元学习的效果并不理想。它在策略和目标函数之间缺乏明确的区分，因此很容易在训练环境中过拟合。与MetaGenRL不同，O(n²)元学习到的参数学习O(n)激活的不平衡加剧了这种情况。

　　最近许多其他的元学习算法学会了策略参数初始化，随后使用固定的RL算法对其进行了微调(Finn et al., 2017; Schulman et al., 2017; Grant et al., 2018; Yoon et al., 2018)。与MetaGenRL不同，这些方法对同一策略参数向量使用二阶梯度，而不是使用单独的目标函数。尽管原则上是通用的(Finn＆Levine, 2018)，但是策略和学习算法的混合导致表达通用更新规则的复杂方式。与RL²相似，可以适应相关任务，但难以推广(Houthooft et al., 2018)。

　　在MetaGenRL之前已经学会了目标函数。Houthooft et al. (2018)逐步发展了一个目标函数，该函数随后用于训练智能体。与MetaGenRL不同，此方法在评估和更新目标函数所需的环境交互次数方面非常昂贵。最近，Bechtle et al. (2019)引入了学到的用于RL的损失函数，该函数也利用了二阶梯度，但使用了策略梯度估计量而不是Q函数。与其他工作类似，他们只关注狭窄的任务分布。学到的目标函数也已用于学习无监督表征(Metz et al., 2019)，用于超参数搜索的DDPG类元梯度(Xu et al., 2018)以及从人类演示中学习(Yu et al., 2018)。在我们工作的同时，Alet et al. (2020)使用从架构搜索的技术来搜索可行的人工好奇心目标，这些目标由原始目标函数组成。

　　Li＆Malik (2016; 2017)和Andrychowicz et al. (2016)通过学习优化器进行元学习，这些优化器通过调节一些固定的目标函数L: 的梯度来更新参数Φ，其中α被学习。它们与MetaGenRL的不同之处在于，它们仅调节固定目标函数L的梯度，而不学习L本身。

　　存在与元学习到的内在奖励函数的另一种联系(Schmidhuber, 1991a; Dayan＆Hinton, 1993; Wiering＆Schmidhuber, 1996; Singh et al., 2004; Niekum et al., 2011; Zheng et al., 2018; Jaderberg et al., 2019)。选择，其中是元学习到的奖励，而是梯度估计量(例如基于价值或基于策略梯度的估计量)表明，学习目标函数包括元学习梯度估计本身，只要它可以由目标Lα上的梯度表示。相反，对于内在奖励函数，梯度估计器通常是固定的。

　　最后，我们注意到，先前已经在迁移学习的背景下显示了不同任务(奖励函数)和环境(例如不同的Atari游戏)之间的积极迁移(Kistler et al., 1997; Parisotto et al., 2015; Rusu et al., 2016; 2019; Nichol et al., 2018)和跨任务的元critic学习(Sung et al., 2017)。与这项工作相反，在这一领域显示出成功的方法完全依赖于人工设计的学习算法。

 

5 EXPERIMENTS

　　我们在几个连续控制基准上研究了MetaGenRL的学习和泛化能力，包括MuJoCo中的HalfCheetah (Cheetah)和Hopper (Todorov et al., 2012)，以及OpenAI gym中的LunarLanderContinuous (Lunar) (Brockman et al., 2016)。这些环境在要控制的基础系统的属性方面以及在必须学习完整环境的动态方面有很大不同。因此，通过在一个环境上训练meta-RL算法并在其他环境上进行测试，它们提供了分布外泛化的合理度量。

　　在我们的实验中，我们将主要与EPG和RL²进行比较，以评估我们方法的有效性。我们还将与几种固定的无模型RL算法进行比较，以衡量MetaGenRL元学习到的算法与这些手工替代方案的比较程度。除非另有说明，否则我们将使用在所示训练环境中平均分布的20个智能体对MetaGenRL进行元训练。元学习使用裁剪的双Q学习，延迟的策略和目标更新以及TD3中的目标策略平滑化(Fujimoto et al., 2018)。在元训练期间，我们将允许每个智能体进行60万个环境交互，然后对1M个交互的目标函数进行元测试。附录B中提供了更多详细信息。

 

5.1 COMPARISON TO PRIOR WORK

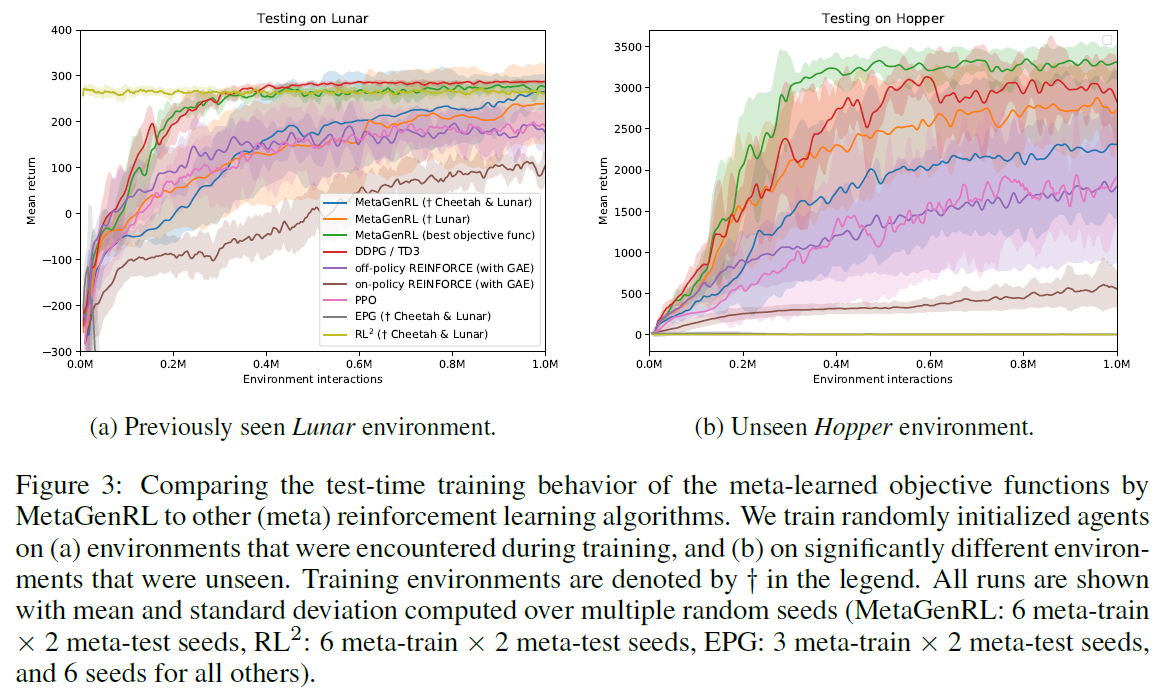
Evaluating on previously seen environments 我们在Lunar上对MetaGenRL进行元训练，并比较其在测试时训练随机初始化的智能体(即使用学到的目标函数并将其固定)到DDPG，PPO以及跨越多个种子的同策/异策REINFORCE(均使用GAE)。图3a显示MetaGenRL明显优于REINFORCE基准和PPO。与找到最优策略的DDPG相比，MetaGenRL平均表现稍差，尽管存在异常值会增加其方差。特别是，我们发现某些元测试智能体在达到最优策略之前会"卡住"一段时间(有关额外分析，参阅第A.2节)。确实，当仅评估在元训练期间元学习到的最优目标函数(图3a中的MetaGenRL(最优目标函数))时，我们能够观察到方差大大降低，甚至性能更高。

　　当在Lunar和Cheetah上对MetaGenRL进行元训练时，我们还报告了结果(图3a)，并与在相同环境下经过元训练的EPG和RL²进行了比较⁶。对于MetaGenRL，在这种情况下，我们能够获得与仅在Lunar上进行元训练相似的性能。相反，对于EPG，可以观察到甚至十亿个环境交互也不足以找到好的目标函数(在图3a中迅速下降到-300以下)。最后，我们发现RL²经过1亿次元训练迭代后达到了最优策略，并且其性能不受Lunar测试期​​间额外步骤的影响。我们注意到RL²并没有将策略和学习规则区分开，实际上在类似的"分布内"评估中，RL²被认为是成功的(Wang et al., 2016; Duan et al., 2016)。

　　表1为其他两个环境提供了类似的比较。在这里，我们发现，一般而言，MetaGenRL能够胜过REINFORCE基准和PPO，并且在大多数情况下(除了Cheetah)，其性能类似于DDPG⁷。我们还发现，MetaGenRL始终胜过EPG，并且经常胜过RL²。有关在两个以上环境中进行元训练的分析，请参阅附录A。

Generalization to vastly different environments 我们评估了MetaGenRL，EPG和RL²在Hopper上学到的相同的目标函数，这与元训练环境相比有显著差异。图3b显示，MetaGenRL学到的目标函数继续胜过PPO和我们的REINFORCE实现，而性能最优的配置甚至可以胜过DDPG。

　　与相关的meta-RL方法进行比较时，我们发现MetaGenRL在这种情况下明显更好。EPG的性能仍然很差，考虑到以前看过的环境，这是可以预期的。另一方面，我们现在发现RL²基准完全失败(导致平坦的低奖励评估)，这表明以前发现成功的学习规则实际上完全过拟合于在元学习训练期间看到的环境。当使用表1和附录A中报告的不同训练和测试环境划分时，我们能够观察到相似的结果。

 

⁵ A.3节中的消融研究表明确实需要大量智能体。
⁶ 为了确保获得良好的基准，我们允许RL²最多进行100M个环境交互，EPG最多允许1B个环境交互，这是MetaGenRL所用数量的八/八十倍以上。关于EPG，这确实要求我们将随机种子总数减少到3 meta-train x 2 meta-test个种子。

⁷ 我们强调，正在考虑的神经目标函数无法实现DDPG，而在元测试期间仅使用恒定价值估计(即，通过使用梯度停止来使)。

 

5.2 ANALYSIS

5.2.1 META-TRAINING PROGRESSION OF OBJECTIVE FUNCTIONS

　　以前，我们专注于使用目标函数对随机初始化的智能体进行测试时训练，该目标函数经过了元训练，总共进行了60万步(相当于整个群体中总共1200万次环境交互)。现在，我们将研究元训练中目标函数的质量。

　　图4显示了在对Cheetah和Lunar进行元训练期间，以不同的时间间隔在Hopper上评估目标函数的结果。最初(28K步)可以看出，由于缺乏元训练，因此在测试期间获得的回报仅有少量改进。但是，仅元训练86K步后，我们发现(也许令人惊讶)，元训练到的目标函数已经能够在测试期间优化随机初始化的智能体方面取得一致的进展。另一方面，在元训练的这一阶段，我们在测试时观察到很大的方差。在整个元训练的其余阶段中，我们然后观察到收敛速度提高，更新更稳定以及种子之间的方差更低。

 

5.2.2 ABLATION STUDY

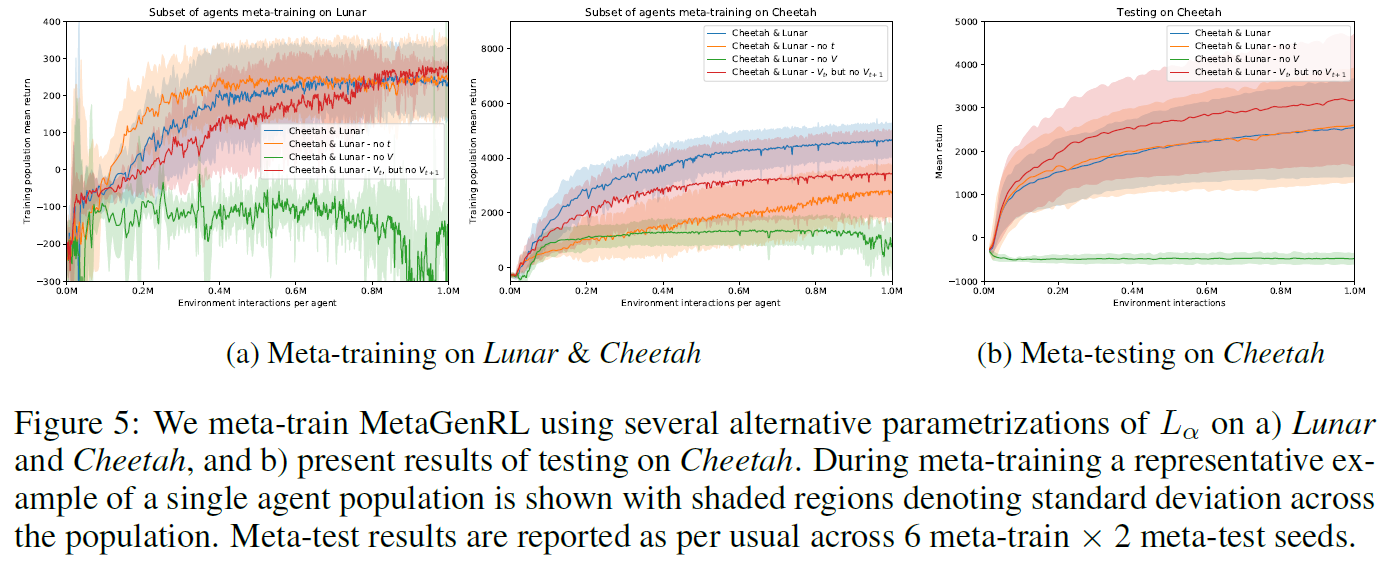
　　我们对第3.2节中描述的神经目标函数进行了消融研究。特别是，我们评估了L_α对价值估计V_t, V_t+1以及在某种程度上可以学到的时间分量的依赖性。包括限制访问所选择的动作或获得的奖励在内的其他消融，对于推广到任何其他环境(或奖励函数)而言，将是灾难性的，因此不予探讨。

 

Dependence on t 我们使用如图2所示的形式为L(a_t, r_t, V_t, π_Φ(s_t)|t ∈ 0, ... , T-1)的参数化目标函数，只是它不在每一步接收有关时间步骤 t 的信息。虽然需要有关当前时间步骤的信息才能学习(例如)广义优势估计(Schulman et al., 2015b)，但LSTM原则上可以自行学习此类时间跟踪，并且我们预计在元训练和元测试中只有很小的影响。确实，在图5b中可以看出，尽管在元训练期间神经目标函数在Cheetah上收敛较慢，但它在不使用 t 的情况下仍能很好地执行(图5a)。

 

Dependence on V 我们使用如图2所示的形式为L(a_t, r_t, t, π_Φ(s_t)|t ∈ 0, ... , T-1)的参数化目标函数，只是它在时间步骤 t 不接收有关价值估计的任何信息。尽管没有替代基准，但存在RL算法，这些算法无需价值函数估计即可工作(例如，Williams (1992); Schmidhuber＆Zhao (1998))，但这些算法通常会有很大的方差。对于图5a中的这种消融，在元训练期间观察到了相似的结果，其中可能存在较大的方差似乎会影响元训练。相应地，在测试期间(图5b)，我们没有发现任何有意义的训练进度。相反，我们发现我们可以消除对价值函数估计之一的依赖，即移除V_t+1，但保留V_t，这在某些运行中甚至可以提高性能。

 

5.2.3 MULTIPLE GRADIENT STEPS

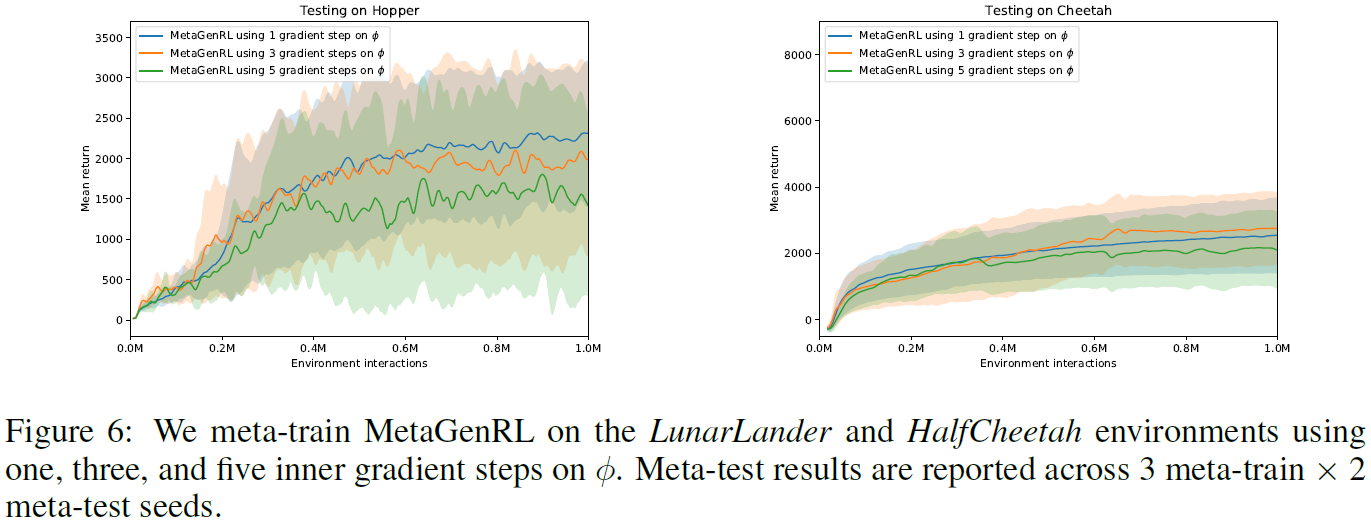
　　我们先分析使用L_α对策略进行多次梯度更新的效果，然后再应用critic针对等式6中的目标函数参数计算二阶梯度。而在先前的实验中，我们仅考虑应用一次更新，梯度更新可能会更好地捕获目标函数的长期影响。同时，进一步远离当前的策略参数可能会降低二阶梯度的总体质量。确实，在图6中可以观察到，在对LunarLander和Cheetah进行元训练之后，在Hopper和Cheetah的测试时训练期间使用3个梯度步骤已经稍微增加了方差。同样，我们发现将梯度步骤数进一步增加到5会损害性能。

 

6 CONCLUSION

　　我们介绍了MetaGenRL，这是一种新颖且异策的基于梯度的元强化学习算法，该算法可利用大量DDPG类智能体来元学习通用目标函数。与相关方法不同，元学习的目标函数不仅可以在狭窄的任务分布中泛化，而且在完全不同的任务上表现出相似的性能，同时明显胜过REINFORCE和PPO。我们认为，这种普遍性归因于MetaGenRL对策略和学习规则的明确分离，后者的函数形式以及在多个智能体和环境中的训练。此外，与EPG相比，二阶梯度的使用将MetaGenRL的采样效率提高了几个数量级(Houthooft et al., 2018)。

　　在未来的工作中，我们的目标是进一步提高元学习到目标函数的学习能力，包括更好地利用先前经验中的知识。实际上，在我们当前的实现中，目标函数无法观察环境或(循环)策略的隐含状态。这些扩展特别有趣，因为它们可能允许学会更复杂的基于好奇心(Schmidhuber, 1991b; 1990; Houthooft et al., 2016; Pathak et al., 2017)或基于模型(Schmidhuber, 1990; Weber et al., 2017; Ha＆Schmidhuber, 2018)的算法。在此程度上，开发自省方法以分析学到的目标函数并扩展MetaGenRL以利用更多环境和智能体将非常重要。

 

A ADDITIONAL RESULTS

A.1 ALL TRAINING AND TEST REGIMES

　　在正文中，我们显示了元训练和测试环境的几种组合。现在，我们将显示所有组合的结果，包括相应的人工设计基准。

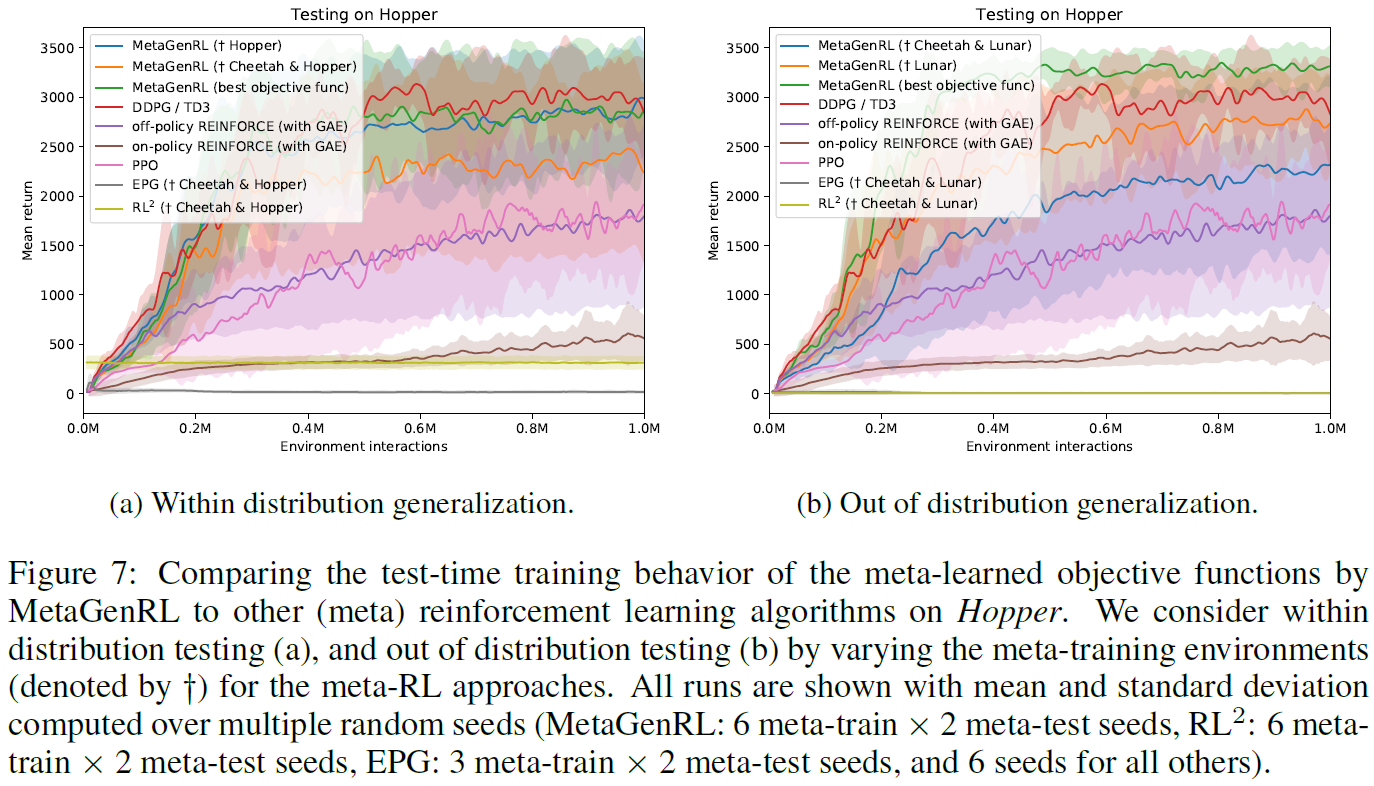
Hopper 在Hopper上(图7)，我们发现MetaGenRL可以很好地发挥作用，无论是对以前见过的环境，还是对未见过的环境的泛化。MetaGenRL明显优于PPO, REINFORCE, RL²和EPG基准的性能。关于RL²，我们观察到只有Hopper包含在元训练中时，它才能获得奖励，尽管它的性能通常很差。关于EPG，我们在对Cheetah和Hopper进行元训练之后，在Hopper进行元测试期间观察到一些学习进度(图7a)，尽管随着测试时训练的进行而迅速下降。相反，在对Cheetah和Lunar进行元训练后，对Hopper进行元测试(图7b)时，根本没有观察到测试时的训练进度。

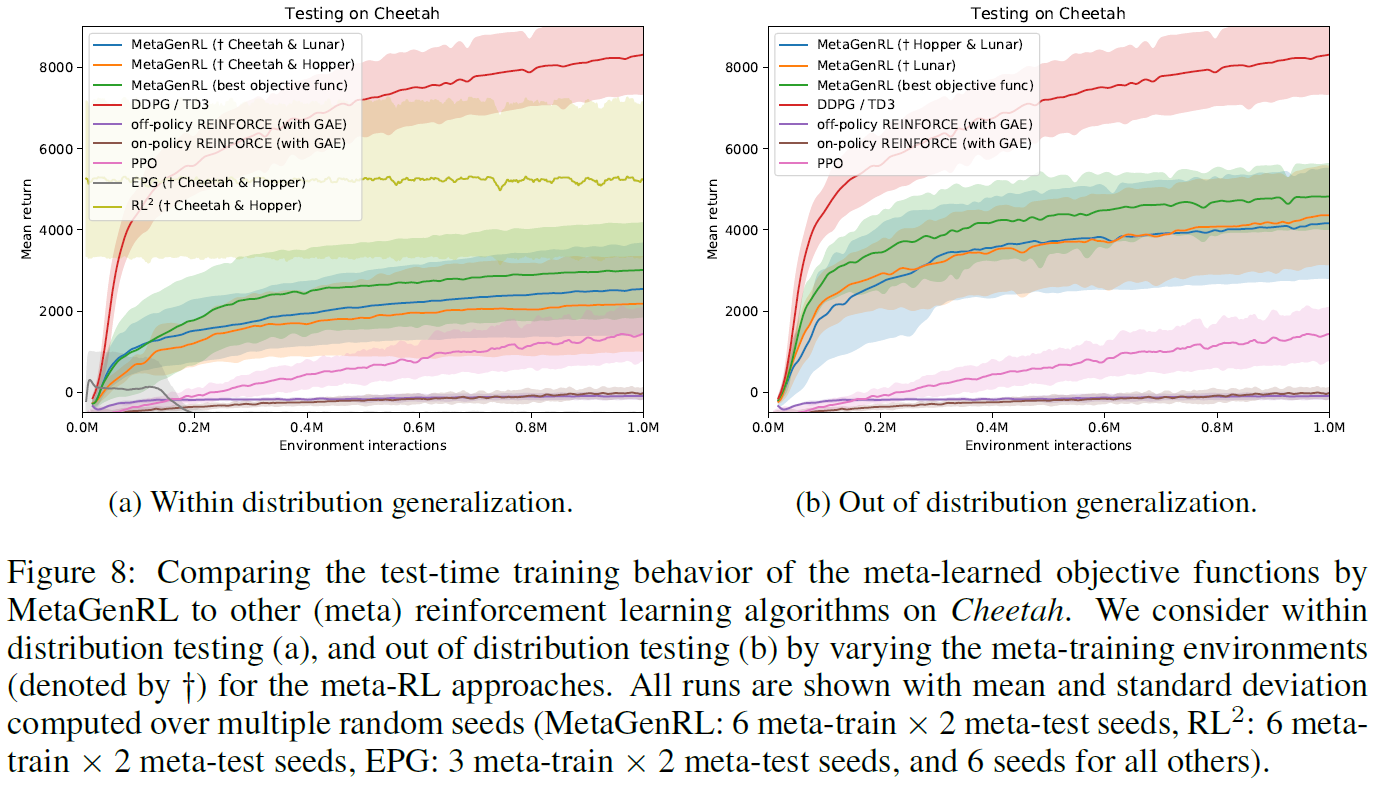
Cheetah 对于Cheetah，在图8中观察到类似的结果，其中MetaGenRL明显优于PPO和REINFORCE。另一方面，可以看出，在这种环境下，DDPG的性能明显优于MetaGenRL。将来进一步研究这些差异以提高我们方法的可表达性将很有趣。关于RL²和EPG，仅在分布泛化结果中可用，这是因为与Hopper和Lunar相比，Cheetah具有更大的观测和/或动作空间。我们观察到RL²的性能与我们先前在Hopper上的发现相似，但是在分布内泛化方面有显著改进(可能是由于过拟合，如在其他划分中一直观察到的)。EPG最初在分布泛化方面显示出更多希望(图8a)，但最终却像以前一样。

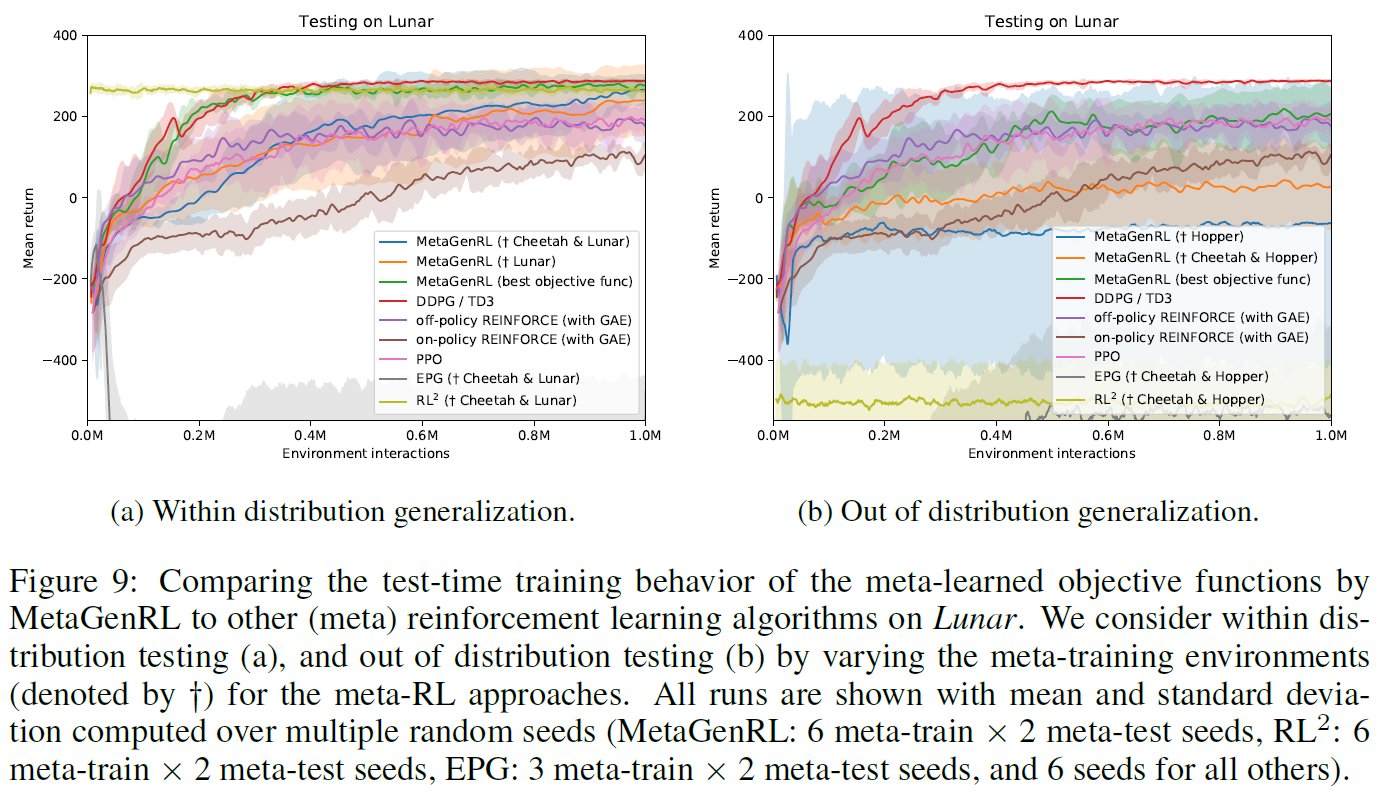
Lunar 在Lunar上(图9)，我们发现在分布泛化方面，MetaGenRL仅比REINFORCE和PPO基准好一点，而在分布外泛化方面则差一些。分析此结果表明，尽管许多运行训练得很好，但有些在训练的早期就被卡住了，没有恢复或延迟恢复。这些异常值导致图9b中MetaGenRL的看似非常大的方差。我们将在A.2节中对此结果进行更详细的分析。如果我们专注于性能最好的目标函数，那么我们会观察到与DDPG相当的性能(图9a)。尽管如此，我们注意到在Hopper上训练的目标函数对Lunar的推广较差，尽管我们先前的结果是，在Lunar上训练的目标函数实际上对Hopper的推广很好。就分布外泛化而言，MetaGenRL仍然能够胜过RL²和EPG。我们确实注意到，EPG能够元学习目标函数，这些目标函数在测试期间可以有所改进。

Comparing final scores 表2显示了与人工设计的基准相比，MetaGenRL获得的最终分数的概述。可以看出，在大多数配置中，MetaGenRL的性能均优于PPO和异策/同策REINFORCE，而在三个环境中的两个上带有TD3的DDPG则更胜一筹。请注意，DDPG当前不在MetaGenRL可表示的算法之中。

 

A.2 STABILITY OF LEARNED OBJECTIVE FUNCTIONS

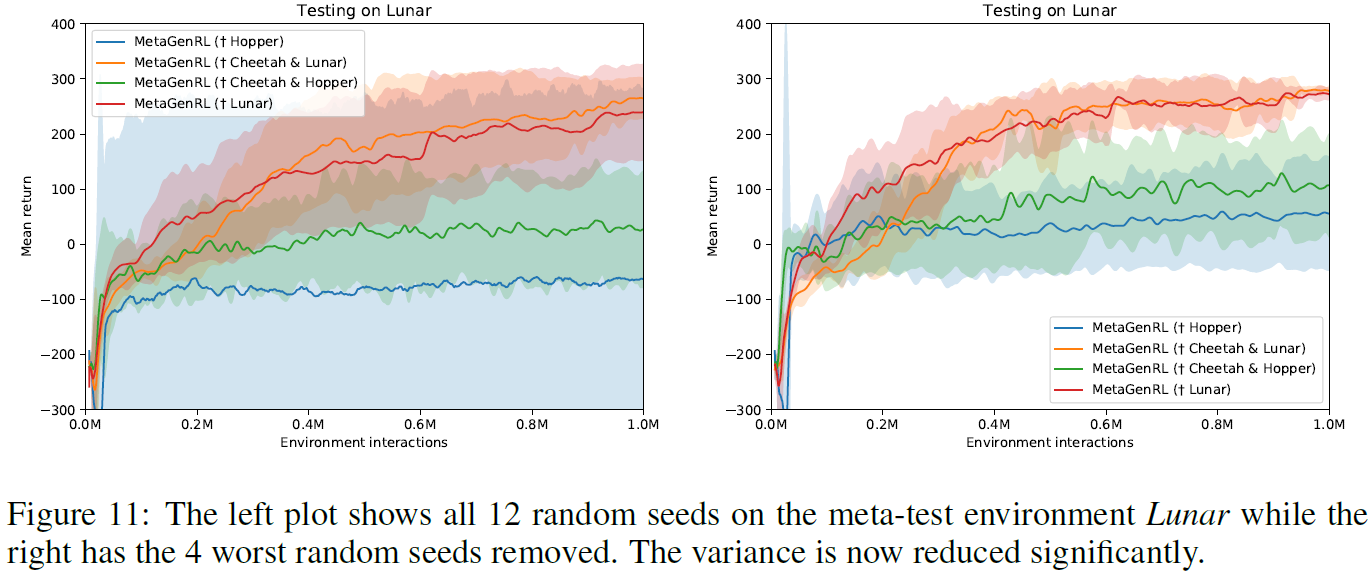
　　在图9的Lunar所示的结果中，我们发现由于异常值，MetaGenRL的看似较大的方差。的确，当分析在Lunar上经过元训练的单独运行并在Lunar上进行测试时，我们发现其中一个运行在训练过程中很早就收敛到局部最优值，此后无法从中恢复。另一方面，我们还观察到，运行可能会长时间卡住，从而使学习进度非常快。这表明在训练的早期阶段，目标函数有时可能难以为策略参数提供有意义的更新。

　　我们通过在图10的整个元训练中的几个时间间隔上评估了一个目标函数，进一步分析了这个问题。从元训练曲线(底部)可以看出，Lunar中的元训练非常早地收敛。这意味着从那时起，目标函数的更新将基于大多数融合的策略。如测试时间图所示，这些额外更新似乎会对测试时间性能产生负面影响。我们假设目标函数本质上是"忘了"训练随机初始化的智能体的早期阶段，而只合并了有关性能良好的智能体的信息。解决此问题的一种可能的方法是将较旧的策略保留在元训练智能体群体中或使用早期停止措施。

　　最后，如果我们排除了四个随机种子(共12个)，则确实发现MetaGenRL观察到的结果的方差显著降低(均值增加)(参见图11)。

 

A.3 ABLATION OF AGENT POPULATION SIZE AND UNIQUE ENVIRONMENTS

　　在我们的实验中，我们在元训练中使用了20个智能体，以确保目标函数需要优化的条件下的多样性。群体规模是稳定进行元优化的关键参数。实际上，在图12中可以看出，随着群体中智能体数量减少，元训练变得越来越不稳定。

　　使用类似的论点，人们期望在元训练期间增加不同环境(或智能体)的数量而受益。为了验证这一点，我们评估了两个额外设置：在分别具有20和40个智能体的Cheetah＆Lunar＆Walker＆Ant上进行元训练。图13显示了针对这些实验在Hopper上进行元测试的结果(另请参见表2中报告的40个智能体的最终结果)。出乎意料的是，我们发现增加不同环境的数量并不能带来明显的改进，实际上，有时甚至会降低性能。一种可能性是，这是由于所考虑的目标函数的简单形式所致，它无法访问环境观测值以有效区分它们。另一种可能性是，MetaGenRL的超参数需要进行其他调整才能与这些设置兼容。

 

B EXPERIMENT DETAILS

　　在下文中，我们将描述有关所用结构，元训练，超参数和基准的所有实验细节。可以在http://louiskirsch.com/code/metagenrl上找到重现我们实验的代码。

 

B.1 NEURAL OBJECTIVE FUNCTION ARCHITECTURE

Neural Architecture 在这项工作中，我们使用LSTM来实现目标函数(图2)。LSTM在所考虑的轨迹期间遇到的状态，动作和奖励元组在时间上反向运行。在每个步骤 t，LSTM接收作为奖励的输入r_t，当前和先前状态的价值估计V_t, V_t+1，当前时间步骤 t 以及最后在当前时间步骤采取的动作a_t以及当前策略π_Φ(s_t)确定的动作。首先通过跨越动作维度的一维卷积层来处理动作，然后减去均值。这允许环境之间的动作大小不同。假设A(B) ∈ R^1xD是来自回放缓存的动作，A^(π) ∈ R^1xD是该策略预测的动作，W ∈ R^2xN是与N个传出单元相对应的可学习矩阵，然后这些动作按照下式转换：

其中[a, b]是沿第一个轴的a和b的串联。这对应于核大小为1且步长为1的卷积。如有必要，可以在应用W后添加具有非线性的进一步转换。我们发现将ReLU激活用于一半单位是有帮助的(但并非绝对必要)，而对另一半使用平方激活。

　　在每个时间步骤，LSTM输出标量值l_t(在-η到η的范围内，并使用scaled tanh激活)，将其求和以获得神经目标函数的值。相对于策略参数Φ对此值进行微分，然后产生可用于改进的梯度。我们只允许梯度从π_Φ(s_t)向后流向Φ。该实现与使用广义优势估计(Schulman et al., 2015b)的REINFORCE估计器(Williams, 1992)的函数形式密切相关。
　　所有前馈网络(critic和策略)都使用ReLU激活和层归一化(Ba et al., 2016)。LSTM使用tanh激活进行单元和隐含状态转换，使用sigmoid激活进行门操作。输入时间 t 在回合开始时的0和最终转换时的1之间归一化。表3列出了任何其他超参数。

 

Extensibility 目标函数的可表达性可以通过几种方式进一步提高。一种可能性是将状态观察的整个序列o_1:T添加到其输入中，或者通过引入双向LSTM来实现。其次，可以将有关策略的其他信息(例如，循环策略的隐含状态)提供给L。尽管在这项工作中没有进行探讨，但是从原则上讲，这将使人们能够学习鼓励某些表征出现的目标，例如类似于世界模型的关于未来观测的预测表征(Schmidhuber, 1990; Ha＆Schmidhuber, 2018; Weber et al., 2017)。反过来，这些可能会产生压力，使策略动作适应环境中未知的动态(Schmidhuber, 1991b; 1990; Houthooft et al., 2016; Pathak et al., 2017)。

 

B.2 META-TRAINING

Annealing with DDPG 在元训练的开始(学习L_α)，目标函数是随机初始化的，因此不会对策略进行明智的更新。这可能导致在训练过程中不可逆转地违反策略。我们当前的实现通过使用DDPG 对前10k个时间步骤(所有时间步骤的2％)进行线性退火来解决此问题。初步实验表明，在前10k步的梯度上的指数学习率表可以用DDPG代替退火。学习速率在零和1e-3的学习速率之间呈指数级退火。但是，在极少数情况下，这仍然可能导致训练运行失败，因此，我们在当前工作中省略了这种方法。

 

Standard training 在训练过程中，与TD3 (Fujimoto et al., 2018)相似，critic的更新速度是策略和目标函数的两倍。对于从环境中收集的每个时间步骤，将使用从回放缓存中采样的数据进行一次梯度更新。公式6中关于Φ的梯度是通过标准方式使用固定学习率进行组合的，所有其他参数更新均使用具有默认参数的Adam (Kingma＆Ba, 2015)。表3和表4中可以看到任何其他超参数。

 

Using additional gradient steps 在我们的实验(第5.2.3节)中，我们分析了在应用critic针对目标函数参数计算二阶梯度之前，使用L_α对策略应用多个梯度更新的效果。对于两次更新，这给出了下式：

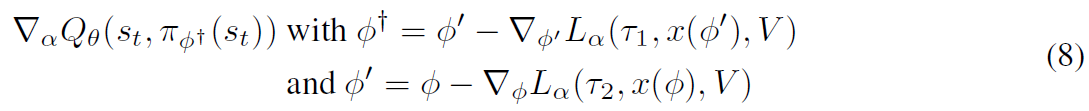
并且可以相应地扩展到两个以上。此外，我们使用不相交的小批量数据τ：τ₁, τ₂。当使用更新策略时，我们将继续仅使用单个梯度步骤。

 

B.3 BASELINES

RL² RL²的实现模仿了Duan et al. 的论文(Duan et al., 2016)。但是，我们在MuJoCo环境中使用TRPO (Schulman et al., 2015a)无法获得良好的结果，因此使用了PPO (Schulman et al., 2017)。PPO超参数及其实现取自rllib (Liang et al., 2018)。我们的实现使用具有64个单位的LSTM，并且不会连续两个回合重置LSTM的状态。在额外回合后重置不能改进训练效果。通过使用环境包装器适当地填充零，可以处理整个环境中不同的动作和观察维度。

 

EPG 我们使用原始论文中的官方EPG代码库https://github.com/openai/EPG (Houthooft et al., 2018)。超参数摘自本文，V = 64噪声矢量，更新频率M = 64，每个内环更新128次，从而内环长度为8196步。在元测试的训练期间，我们以相同的更新频率运行，共计100万步。

 

PPO & On-Policy REINFORCE with GAE 我们使用https://spinningup.openai.com/en/latest/spinningup/bench.html中包含GAE (Schulman et al., 2015b)基准的优化实现。

 

Off-Policy Reinforce with GAE 除了将目标函数固定为具有GAE (Schulman et al., 2015b)基准的REINFORCE估计量之外，该实现与MetaGenRL等效。因此，经验是从回放缓存中采样的。我们还对重要性加权的无偏估计量进行了实验，但这导致性能不佳。

 

DDPG 我们的实现基于https://spinningup.openai.com/cn/latest/spinningup/bench.html并使用与MetaGenRL相同的TD3技巧(Fujimoto et al., 2018)和超参数(如果适用)。