RL^2: Fast Reinforcement Learning via Slow Reinforcement Learning

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

ICLR 2017

 

ABSTRACT

　　深度RL已经成功地自动学习了复杂的行为。但是，学习过程需要大量的试验。相比之下，动物可以通过几次试验而学习新的任务，这得益于它们对世界的了解。本文力图弥合这一差距。与其设计一种"快速"的RL算法，不如将其表示为RNN并从数据中学习。在我们提出的方法RL²中，该算法以RNN的权重进行编码，这些权重是通过通用("慢速")RL算法缓慢学习的。RNN接收典型RL算法将接收的所有信息，包括观察，动作，奖励和终止标志；并且在给定的马尔可夫决策过程(MDP)中跨回合保留其状态。RNN的激活将"快速"RL算法的状态存储在当前(以前未见过)的MDP上。我们在小规模和大规模问题上通过实验评估RL²。在小规模方面，我们训练它来解决随机生成的多臂赌博机问题和有限的MDP。训练完RL²后，它在新MDP上的性能接近人工设计的算法，并具有最优性保证。在大规模方面，我们在基于视觉的导航任务上对RL²进行了测试，并表明它可以扩展到高维问题。

 

1 INTRODUCTION

　　近年来，深度RL取得了许多令人印象深刻的结果，包括从原始像素玩Atari游戏(Guo et al., 2014; Mnih et al., 2015; Schulman et al., 2015)，并获得了先进的操纵和移动技能(Levine et al., 2016; Lillicrap et al., 2015; Watter et al., 2015; Heess et al., 2015; Schulman et al., 2015; 2016)。但是，许多成功是以高样本复杂性为代价的。例如，最新的Atari结果需要每个游戏数以万计的经验回合(Mnih et al., 2015)。要掌握一款游戏，你需要花费近40天的时间不停地玩游戏。相比之下，人类和动物在极少数的试验中就能够学习新任务。继续前面的示例，Mnih et al. (2015)中的人类角色只需要2个小时的经验即可掌握游戏。我们认为，这种强烈对比的原因主要是由于缺乏良好的先验，这导致这些深度RL智能体需要从头开始重建它们对世界的了解。

　　尽管贝叶斯RL为将先验知识整合到学习过程中提供了坚实的框架(Strens, 2000; Ghavamzadeh et al., 2015; Kolter＆Ng, 2009)，但贝叶斯更新的精确计算在除最简单的情况以外的所有条件下都是棘手的。因此，实用的RL算法通常将贝叶斯和特定领域的思想相结合，以降低样本的复杂性和计算负担。值得注意的例子包括动态未知的指导性策略搜索(Levine and Abbeel, 2014)和PILCO (Deisenroth and Rasmussen, 2011)。这些方法可以使用几分钟到几小时的实际经验来学习任务，而以前的方法则需要几天甚至几周(Schulman et al., 2015; 2016; Lillicrap et al., 2015)。但是，这些方法倾向于对环境进行假设(例如，在学习时使用仪器来访问状态)，或者在高维环境中变得难以计算(Wahlström et al., 2015)。

　　与手动设计特定领域的RL算法不同，本文采用了另一种方法：我们将智能体本身的学习过程视为目标，可以使用标准RL算法对其进行优化。该目标是根据特定分布在所有可能的MDP上平均的，这反映了我们想提炼到智能体中的先验条件。我们将主体构造为RNN，除了正常接收到的观察结果外，该网络还接收过去的奖励，动作和终止标志作为输入。此外，其内部状态在各个回合之间得以保留，因此它具有以自身隐含激活进行学习的能力。因此，学到的智能体也充当学习算法，并且在部署时可以适应手头的任务。

　　我们对两组经典问题(多臂赌博机和表格式MDP)进行评估。这些问题已被广泛研究，并且存在实现渐近最优性能的算法。我们证明了名为RL²的方法可以实现与这些理论上合理的算法相当的性能。接下来，我们在使用ViZDoom环境实现的基于视觉的导航任务上评估RL²(Kempka et al., 2016)，表明RL²也可以扩展到高维问题。

 

2 METHOD

2.1 PRELIMINARIES

 

2.2 FORMULATION

　　现在，我们描述我们的公式，该公式将学习RL算法视为一种RL问题，因此命名为RL²。我们假设知道一组MDP，用M表示，并且其上的分布ρ_M：M → R₊。我们只需要从这个分布中采样。我们使用n表示允许在特定MDP上花费的回合总数。我们将试验定义为与固定MDP的一系列交互回合。

　　智能体与环境之间的交互过程如图1所示。这里，每个试验恰好由两个回合组成，因此n =2。对于每个试验，从ρ_M抽取一个单独的MDP，对于每个回合，从特定于相应MDP的初始状态分布中抽取一个新的s₀。在接收到由智能体产生的动作时，环境计算奖励r_t，前向计算下一个状态s_t+1。如果回合已终止，则会将终止标志d_t设置为1，否则默认为0。将下一个状态s_t+1，动作a_t，奖励r_t和终止标志d_t组合在一起，形成策略的输入¹，它以隐含状态h_t+1为条件，生成下一个隐含状态h_t+2和动作a_t+1。在回合结束时，策略的隐含状态将保留到下一个回合，但不会在两次试验之间保留。

　　此公式下的目标是在单个试验而不是单个回合中最大化期望的总折扣奖励。最大化这一目标等同于最小化累积伪遗憾(Bubeck＆Cesa-Bianchi, 2012)。由于基础MDP在整个试验中都会发生变化，因此只要不同的MDP需要不同的策略，智能体就必须根据其对当前所使用的MDP的信念采取不同的动作。因此，智能体被迫整合已收到的所有信息 ，包括过去的动作，奖励和终止标志，并不断调整其策略。因此，我们建立了一个端到端的优化过程，在该过程中，鼓励智能体学习"快速"的RL算法。

　　为了阐明清楚，我们将"内部"问题(智能体在每个试验中都看到n个问题)定义为MDP而不是POMDP。但是，该方法也可以在部分观察的情况下应用，而无需进行任何概念上的更改。在部分观察的设置中，智能体面对一系列POMDP，并且在时间 t 接收观察o_t而不是状态s_t。3.3节中的视觉导航实验实际上是此POMDP设置的一个实例。

 

¹ 为确保输入的维度一致，我们将占位符值用作策略的初始输入。

 

2.3 POLICY REPRESENTATION

　　我们将策略表示为一般的RNN。每个时间步骤都接收元组(s, a, r, d)作为输入，使用函数Φ(s, a, r, d)嵌入该元组并将其作为输入提供给RNN。为了减轻由于梯度消失和爆炸而导致的难以训练RNN的问题(Bengio et al., 1994)，我们使用门控循环单元(GRU)(Cho et al., 2014)，已证明具有良好的经验性能(Chung et al., 2014; Józefowicz et al., 2015)。GRU的输出被馈送到全连接层，然后是softmax函数，该函数形成动作上的分布。

　　我们还尝试了替代结构，该结构显式重置了采样的MDP的每个回合的部分隐含状态，但没有发现对上述简单结构的任何改进。

 

2.4 POLICY OPTIMIZATION

　　将任务表述为RL问题后，我们可以轻松地使用标准的现成RL算法来优化策略。我们使用信任域策略优化(TRPO)的一阶实现(Schulman et al., 2015)，因为它具有出色的经验性能，并且不需要过多的超参数调整。有关更多详细信息，请参见原始论文。为了减少随机梯度估计中的方差，我们使用一个基准，该基准也表示为使用GRU作为构建基块的RNN。我们可以选择应用广义优势估计(GAE)(Schulman et al., 2016)来进一步减少方差。

 

3 EVALUATION

　　我们设计了实验来回答以下问题：

• 相对于文献中提出的针对这种结构量身定制的现有算法，RL²是否可以学习在具有特殊结构的MDP类上实现性能良好的算法？
• RL²是否可以扩展到高维任务？

　　对于第一个问题，我们在两组任务(多臂赌博机(MAB)和表格式MDP)上评估RL²。这些问题已在RL文献中得到了广泛的研究，并且本文的工作内容包括具有渐近最优性保证的算法。我们证明了我们的方法可以达到与这些理论上合理的算法相当的性能。 

　　对于第二个问题，我们在基于视觉的导航任务上评估RL²。我们的实验表明，学到的策略可以有效地利用学到的视觉信息以及从先前回合中获得的短期信息。

 

3.1 MULTI-ARMED BANDITS

　　多臂赌博机问题是一个MDP的子集(其中智能体环境为无状态)。具体来说，有k个臂(动作)，并且在每个时间步骤，智能体拉动其中一个臂，例如 i，并接收从未知分布中抽取的奖励：我们的实验将每个臂设为参数为p_i的伯努利分布。目标是最大化在固定数量的时间步骤上获得的总奖励。关键的挑战是平衡探索与开发之间的关系——"探索"每个臂足够的次数以估计其分布(p_i)，但最终切换到最优臂的"开发"。尽管多臂赌博机问题很简单，但他们的研究产生了丰富的理论和一系列具有最优性保证的算法。

　　使用RL²，我们可以通过在给定分布ρ_M上训练RNN策略来解决赌博机问题。如果学习成功，则所产生的策略应能够与理论上最优的算法相比。我们通过从[0, 1]上的均匀分布中采样每个参数p_i来随机产生赌博机问题。在使用RL²训练RNN策略之后，我们将其与以下策略进行了比较：

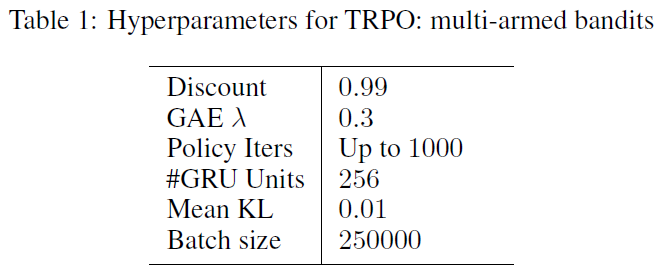
　　贝叶斯方法(Gittins指数和Thompson采样)利用分布ρ_M；并且我们为这些方法提供了真实分布。对于具有超参数的每种方法，我们通过对每个实验设置进行单独的网格搜索来最大化得分。附录中显示了用于TRPO的超参数。

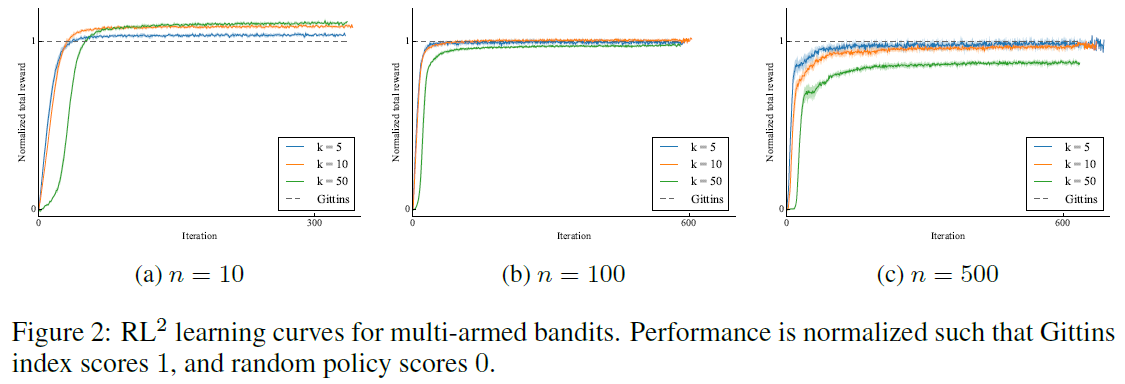
　　结果总结在表1中。各种设置的学习曲线如图2所示。我们观察到，我们的方法所达到的性能几乎与参考方法一样好，而参考方法是专门为在多臂赌博机问题上表现出色而(人为)设计的。值得注意的是，已发布的算法主要是为了最大程度地减少渐近遗憾(而不是有限时间范围遗憾)而设计的，因此在有限时间范围设置中仍有一些可以胜过它们的空间。

　　我们观察到，在最具挑战性的情况下，Gittins指数与RL²之间存在明显差距，共有50个臂和500个回合。这就提出了一个问题，即应该探索更好的架构还是更好的(慢速)RL算法。为了确定瓶颈，我们使用监督学习来训练相同的策略结构，并使用Gi​​ttins指数方法生成的轨迹作为训练数据。我们发现，在测试域中执行后，学到的策略可以达到与Gittins指数方法相同的性能水平，这表明使用更好的RL算法仍有改进的余地。

 

3.2 TABULAR MDPS

 

3.3 VISUAL NAVIGATION

 

4 RELATED WORK

　　过去已经以各种形式探讨了使用先验经验来加快RL算法的概念。早期的研究以元学习的形式研究了诸如学习率和温度之类超参数的自动调整(Ishii et al., 2002; Schweighofer＆Doya, 2003)。Wilson et al. (2007)使用分层贝叶斯方法来维持后验动态的可能模型，并根据后验应用乐观的Thompson采样。分层RL中的许多工作提出从以前的任务中提取可重用的技能，以加快在新任务中的探索(Singh, 1992; Perkins et al., 1999)。我们请读者参考Taylor＆Stone (2009)，以更全面地了解多任务和迁移学习方面。

　　最近，Fu et al. (2015)提出了一种基于iLQG的有模型方法，该模型具有未知的动态特性(Levine & Abbeel, 2014)，该方法使用从先前任务中收集的样本在动态之前构建了一个神经网络，并且可以在新的相关任务上进行one-shot学习(为了减少样本的复杂性)。使用深度神经网络进行多任务学习和迁移学习的兴趣日益浓厚(Parisotto et al., 2015; Rusu et al., 2015; 2016a; Devin et al., 2016; Rusu et al., 2016b)。

　　在更广泛的机器学习环境中，人们对目标分类的one-shot学习有很大的兴趣(Vilalta＆Drissi, 2002; Fei-Fei et al., 2006; Larochelle et al., 2008; Lake et al., 2011; Koch, 2015)。我们的工作从特定的工作中汲取了灵感(Younger et al., 2001; Santoro et al., 2016; Vinyals et al., 2016)，该方法将元学习公式化为优化问题，因此可以通过梯度下降进行端到端的优化。这些工作适用于监督学习设置，而我们的工作适用于更一般的RL设置。尽管RL设置更具挑战性，但最终的行为却更加丰富：我们的智能体不仅必须学习利用现有信息，还必须学习探索，这通常不是监督学习中的一个问题。另一项工作(Hochreiter et al., 2001; Younger et al., 2001; Andrychowicz et al., 2016; Li＆Malik, 2016)研究了优化过程中的元学习。在那里，元学习器对参数化模型进行显式更新。相比之下，我们不使用直接参数化的策略。相反，RNN智能体同时充当元学习器和生成的策略。

　　我们的智能体实质上构成了部分可观察的MDP(POMDP)，该MDP在外环中得以解决，在该外环中，潜在的MDP未被智能体观察到。这种将未知MDP还原为POMDP的过程可以追溯到双重控制理论(Feldbaum, 1960)，其中"双重"是指人们既控制状态又控制状态估计。Feldbaum指出，原则上可以通过动态编程来计算解决方案，但是这样做通常是不切实际的。具有这种结构的POMDP也已经以"混合可观察性MDP"的名称进行了研究(Ong et al., 2010)。然而，那里提出的方法面临解决高维POMDP的常规挑战。

 

5 DISCUSSION

　　本文提出了一种设计更好的RL算法的不同方法：与其按照自己的设计者采取动作，不如使用标准RL技术来端对端地学习算法。也就是说，"快速"RL算法是一种状态存储在RNN激活中的计算，而RNN的权重是通过通用的"慢速"RL算法来学习的。我们的方法RL²已证明在小规模环境下具有与理论上最优算法相比的能力。我们进一步展示了其扩展到高维任务的潜力。

　　在实验中，我们发现了改进RL²的机会：外环RL算法被证明是一个立即的瓶颈，并且我们认为，对于具有极长时间范围的设置，该策略可能还需要更好的结构。尽管我们为外环算法和策略使用了通用的方法和结构，但是这样做也忽略了基础的回合结构。我们期望利用问题结构的算法和策略结构来显著提高性能。

 

APPENDIX

A DETAILED EXPERIMENT SETUP

　　所有实验的共同点：如2.2节所述，必要时我们使用占位符值。例如，在t = 0时，没有先前的动作，奖励或终止标志。由于我们所有的实验都使用离散动作，因此我们将动作0的嵌入用作动作的占位符，将0用于奖励和终止标志。为了形成对GRU的输入，我们按原样使用奖励和终止标志的值，并按照下面分别针对每个实验所述的方式嵌入状态和动作。然后将这些值连接在一起以形成联合嵌入。
　　对于神经网络架构，我们在整个实验过程中都使用ReLU作为隐含激活，并且对所有权重矩阵应用去除数据依赖初始化的权重归一化(Salimans＆Kingma, 2016)。隐含到隐含的权重矩阵使用正交初始化(Saxe et al., 2013)，所有其他权重矩阵都使用Xavier初始化(Glorot＆Bengio, 2010)。我们将所有偏差向量都初始化为0。除非另有说明，否则策略和基准将使用具有相同结构的独立神经网络，直到最后一层，其中输出数量有所不同。
　　所有实验均使用TensorFlow (Abadi et al., 2016)和rllab (Duan et al., 2016)实现。我们使用TabulaRL软件包提供的经典算法的实现(Osband, 2016)。

 

A.1 MULTI-ARMED BANDITS

　　表1中显示了TRPO的参数。由于环境是无状态的，因此我们使用常数嵌入0作为占位符来代替状态，并对动作进行one-hot嵌入。

 

A.2 TABULAR MDPS

 

A.3 VISUAL NAVIGATION