Learning to Reinforcement Learn

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

CogSci, (2017)

 

ABSTRACT

　　近年来，深度RL系统在许多具有挑战性的任务领域中都获得了超出人类的性能。但是，此类应用的主要局限性在于它们对大量训练数据的需求。因此，当前的一个关键目标是开发能够快速适应新任务的深度RL方法。在当前的工作中，我们介绍了应对这一挑战的新颖方法，我们将其称为深度元RL。先前的工作表明，循环网络可以在完全受监督的上下文中支持元学习。我们将此方法扩展到RL设置。出现的是使用一种RL算法训练的系统，但其循环动态实现了第二个非常独立的RL程序。第二个学习到的RL算法可以在任意方面与原始算法不同。重要的是，由于它是被学习的，因此将其配置为利用训练域中的结构。我们通过一系列七个概念验证实验来解开这些问题，每个实验都检验了深度元RL的关键方面。我们考虑了扩展与扩大该方法的前景，并指出了对神经科学潜在的重要意义。

 

1 INTRODUCTION

　　最新的进展使得RL方法得以扩展到Atari (Mnih et al., 2015)和Go (Silver et al., 2016)这样复杂且大规模的任务环境中。关键的突破是技术的发展，该技术可以通过深度学习(LeCun et al., 2015; Mnih et al., 2015)将RL与非线性函数近似进行稳定集成。由此产生的深度RL方法在越来越多的域中达到了人类甚至超出人类水平的性能(Jaderberg et al., 2016; Mnih et al., 2015; Silver et al., 2016)。但是，它们至少明显缺少人类性能的两个方面。首先，深度RL通常需要大量的训练数据，而人类学习者只需很少的经验就可以在各种各样的任务中获得合理的性能。其次，深度RL系统通常专注于一个受限的任务领域，而人类学习者可以灵活地适应不断变化的任务条件。最近的批评(例如Lake et al., 2016)将这些差异称为对当前深度RL研究的直接挑战。

　　在当前的工作中，我们概述了应对这些挑战的框架，我们将其称为深度元RL，旨在将其与以前的工作联系在一起并与使用“元RL”一词的工作(例如，Schmidhuber et al., 1996; Schweighofer and Doya, 2003，稍后讨论)区分开来。关键概念是使用标准深度RL技术来训练RNN，以使循环网络开始实现自己的独立RL程序。正如我们将说明的那样，在适当的情况下，次级学习到的RL程序可以显示原始RL程序所缺乏的适应性和样本效率。

　　以下各节回顾了在元学习中采用RNN的先前工作，并描述了将此类方法扩展到RL设置的一般方法。然后，我们提出了七个概念验证实验，每个实验都通过根据此框架刻画智能体性能来强调深度元RL设置的重要分支。最后，我们讨论了下一步研究的主要挑战以及对神经科学的潜在影响。

 

2 METHODS

2.1 BACKGROUND: META-LEARNING IN RECURRENT NEURAL NETWORKS

　　灵活且高效的数据学习自然需要先验偏差的操作。概括地说，这种偏差可以来自两个方面。它们可以被设计到学习系统中(例如，在卷积网络中)，或者它们本身可以通过学习获得。在机器学习文献中，在元学习的主题下探讨了第二种情况(Schmidhuber et al., 1996; Thrun and Pratt, 1998)。
　　在一个标准设置中，学习智能体面临一系列任务，这些任务彼此不同，但也共享一些基本规则。然后，元学习被定义为一种效果，通过这种效果，智能体可以比过去的任务更快地提高其在每个新任务中的性能(Thrun and Pratt, 1998)。在结构层面上，元学习通常被概念化为涉及两个学习系统：一个较低级别的系统，它学习相对较快，并且主要负责适应每个新任务；较慢的上级系统，该系统可跨任务工作以调整和改进下级系统。

　　在深度学习社区内外，已经探索了各种方法来实现这种基本的元学习设置(Thrun and Pratt, 1998)。这里特别相关的是Hochreiter和同事(Hochreiter et al., 2001)引入的方法，其中使用标准的反向传播对一系列相关任务训练RNN。其设置的关键方面是，网络在任务中的每个步骤上都会接收一个辅助输入，该辅助输入指示上一步的目标输出。例如，在回归任务中，在每个步骤中，网络都会收到一个x值作为输入，希望为其输出对应的y，但是网络也会收到一个输入，该输入公开了先前步骤的目标y值(参见Hochreiter et al., 2001; Santoro et al., 2016)。在这种情况下，在每个训练回合中将使用不同的函数来生成数据，但是如果所有函数均来自单个参数族，则系统会逐渐调整为这种一致的结构，从而在整个过程中越来越快地收敛于跨回合的准确输出。
　　Hochreiter方法的一个有趣方面是，每个新任务中学习的基础过程完全位于循环网络的动态范围内，而不是用于调整网络权重的反向传播过程。实际上，在初始训练期之后，即使权重保持恒定，网络也可以提高其在新任务上的性能(另请参见Cotter and Conwell, 1990; Prokhorov et al., 2002; Younger et al., 1999)。该方法的第二个重要方面是，在循环网络中实现的学习过程适合于网络训练的跨任务族的结构，并嵌入了一些偏差，使其在处理来自该族的任务时可以有效地学习。

 

2.2 DEEP META-RL: DEFINITION AND KEY FEATURES

　　重要的是，Hochreiter的原始工作(Hochreiter et al., 2001)及其后续扩展(Cotter and Conwell, 1990; Prokhorov et al., 2002; Santoro et al., 2016; Younger et al., 1999)只涉及了监督学习(即，每个步骤提供的辅助输入都明确指示了上一步的目标输出，并且使用明确的目标对网络进行了训练)。在当前的工作中，我们考虑在RL的背景下采用相同方法的含义。在这里，构成训练系列的任务是相互关联的RL问题，例如，一系列的赌博机问题仅在其参数化方面有所不同。智能体不是将目标输出作为辅助输入，而是接收指示上一步动作输出的输入，以及关键地指示该动作所产生的奖励量的输入。相同的奖励信息与深度RL流程并行提供，该流程可调整循环网络的权重。

　　我们将这种设置及其结果称为“深度元RL”(尽管为了简洁起见，我们通常将其简称为“元RL”，对以前使用过该术语的作者表示歉意)。就像在有监督的情况下一样，当方法成功时，循环网络的动态将实现一种完全不同于用于训练网络权重的学习算法。经过足够的训练后，即使权重保持恒定，学习也可以在每个任务中进行。但是，循环网络在此处执行的过程本身就是一种完善的RL算法，该算法协调了探索与开发的权衡关系，并根据奖励结果改进了智能体的策略。我们将在下文中强调的一个关键点是，该学习到的RL程序可能与用于训练网络权重的算法完全不同。特别是，其策略更新过程(包括该过程的有效学习率等特征)可能与调整网络权重所涉及的策略显著不同，并且学习到的RL过程可以实现其自身的探索方法。至关重要的是，就像在有监督的情况下一样，学习的RL过程将适合跨越多任务环境的统计信息，从而使其能够快速适应新的任务实例。

 

2.3 FORMALISM

　　让我们将马尔可夫决策过程(MDP)的分布(先验)写为D。我们想要证明元RL能够学习先验相关的RL算法，从某种意义上说，它将在从D或D的微小修改获得的MDP上平均表现良好。适当结构化的智能体，嵌入RNN，通过回合与一系列MDP环境(也称为任务)交互来进行训练。在新回合开始时，对新的MDP任务m～D和该任务的初始状态进行采样，并重置智能体的内部状态(即，其循环单元上的激活模式)。然后，智能体程序将在此环境中执行一定离散时间步骤的动作选择策略。在每个步骤 t 处，根据在当前回合期间在MDP m中交互的智能体的整个历史H_t = {x₀, a₀, r₀, ... , x_t-1, a_t-1, r_t-1, x_t}的函数执行动作a_t ∈ A (从回合开始以来观察到的状态{x_s}_0≤s≤t，动作{a_s}_0≤s<t和奖励{r_s}_0≤s<t的集合，当循环单位已重置)。训练网络权重使得在所有步骤和回合中观察到的奖励总和最大化。
　　训练后，智能体的策略是固定的(即权重已冻结，但由于环境的输入和循环层的隐含状态而导致激活发生变化)，并根据从相同的分布D或对该分布的轻微修改中提取的一组MDP对其进行评估(以测试智能体的泛化能力)。在任何新回合的评估开始时，都会重置内部状态。由于智能体了解到的策略是历史相关的(因为它利用循环网络)，因此当暴露于任何新的MDP环境时，它就能够适应和部署优化该任务​​奖励的策略。

 

3 EXPERIMENTS

　　为了评估我们刚刚描述的学习方法，我们进行了一系列的六个概念验证实验，我们将其与相关论文中最初报道的第七个实验一起呈现在这里(Mirowski et al., 2016)。 在这些实验中，特别感兴趣的一点是，根据任何成熟的RL程序的要求，看看是否可以使用元RL来学习探索与开发之间的自适应平衡。第二个也是更重要的焦点是元RL是否可以通过利用任务结构来提高学习效率。

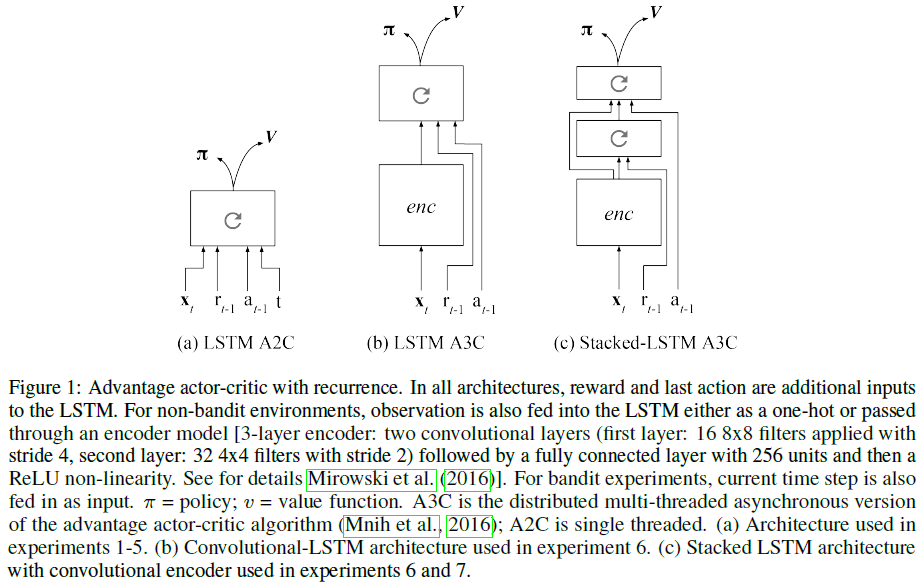
　　为了检查这些问题，我们进行了四个针对赌博机任务的实验，另外两个针对Markov决策问题的实验。我们所有的实验(以及我们报告的其他实验)都采用了一套通用的方法，但实现上的变化很小。在所有实验中，主体架构均以RNN (LSTM; Hochreiter and Schmidhuber, 1997)为中心，馈入代表离散动作的soft-max输出。如下所述，该网络核心的参数以​​及其他一些结构的详细信息在实验中有所不同(请参见图1和表1)。但是，必须强调的是，特定结构之间的比较不在本文讨论范围之内。我们的主要目标是以更一般的方式说明和验证元RL框架。为此，所有实验都使用前面描述的高级任务设置：训练和测试都被组织为固定长度的回合，每个回合都涉及从预定任务分布中随机采样的任务，并在每个回合开始时初始化LSTM隐含状态。结合各个实验描述了特定任务的输入和动作输出。除指定的地方外，在所有实验中，输入都包括标量，该标量指示在前一个时间步骤上收到的奖励及其采样的动作的one-hot表征。

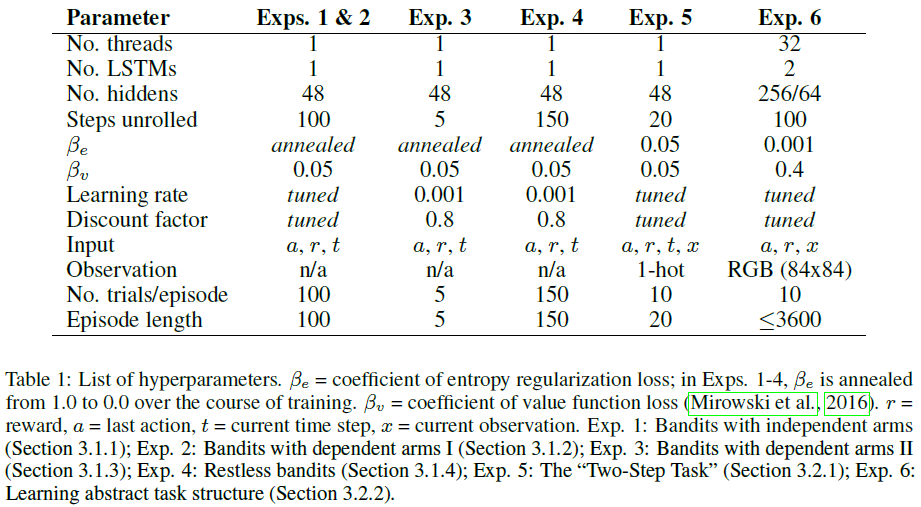
　　所有RL都是使用A2C/A3C算法进行的，详见Mnih et al. (2016)和Mirowski et al. (2016) (另请参见图1)。训练的细节，包括使用熵正则化以及组合的策略和价值估计损失，都紧紧遵循Mirowski et al. (2016)的方法。我们的实验使用单线程，除非另有说明。有关参数的完整列表，请参见表1。

 

3.1 BANDIT PROBLEMS

　　作为评估元RL的初始设置，我们研究了一系列赌博机问题。除了一组非常有限的赌博机环境外，计算(先验依赖的)贝叶斯最优策略是很棘手的。在这里，我们证明，在从给定环境分布中抽取的一组赌博机环境上训练的循环系统，会产生一个赌博机算法，该算法对从该分布中抽取出来的问题表现良好，并且在一定程度上概括了相关分布。因此，元RL学习了先验依赖的赌博机算法。
　　第2.3节中描述的一般元RL过程的特定智能体实例定义如下。令D为赌博机环境下的训练分布。元RL系统通过回合在一系列赌博机环境中进行训练。在新回合开始时，将重置其LSTM状态，并对赌博机任务b~D进行采样。赌博机任务被定义为一组分布(每个臂一个分布)从中抽取奖励。智能体在这种赌博机环境中进行一定数量的试验，并受过训练以使观察到的奖励最大化。经过训练后，将根据从测试分布D'提取的一组赌博机任务对智能体的策略进行评估，该任务既可以与D相同，也可以稍作修改。

　　我们通过累积遗憾评估学习到的赌博机算法的结果性能，累积遗憾衡量了选择次优臂时遭受的损失(期望奖励)。μ_a(b)为在赌博机环境b中臂a的期望奖励，并且μ*(b) = max_a μ_a(b) = μ_a*(b)(b) (其中a*(b)是一个最优臂)为最优期望奖励，我们将(环境b中的)累积遗憾定义为，其中a_t是 t 时刻选择的臂(动作)。在实验4中(不休息的赌博机；第3.1.4节)，也取决于 t。我们以累积遗憾：E_b~D'[R_T(b)]或次优选择次数：。

 

3.1.1 BANDITS WITH INDEPENDENT ARMS

　　我们首先考虑一个简单的双臂赌博机任务，以在存在理论保证和通用算法的条件下检查元RL的行为。臂分布是独立的Bernoulli分布(奖励为1的概率为p，奖励为0的概率为1-p)，其中每个臂的参数(p₁和p₂)均在[0, 1]之间独立均匀采样。我们用D_i表示在这些独立的赌博机环境中的相应分布(其中下标 i 代表独立的臂)。
　　每个回合开始时都会对新的赌博机任务进行采样，并在100次试验中保持不变。训练持续了20000个回合。网络被给予最后一次奖励、最后一次采取的动作和试验编号 t 作为输入，随后产生下一次试验t+1的动作(图1)。训练后，我们对300个新回合进行了评估，将学习率设为零(学到的策略是固定的)。

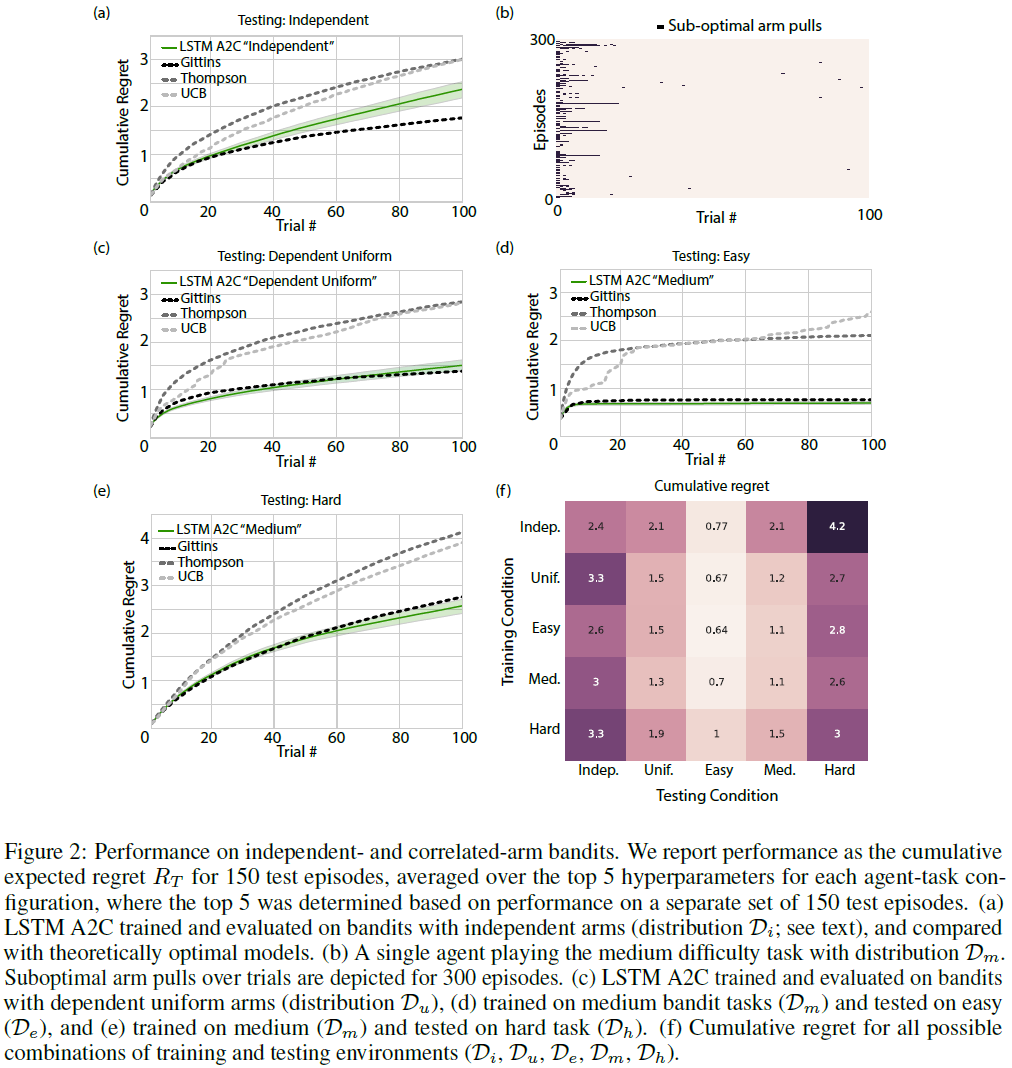
　　在整个模型实例中，我们按照Mnih et al. (2016)的方法随机采样学习率和折扣。对于所有图片，我们绘制了100个随机采样的超参数设置的前5次运行的均值，其中从300个评估回合的前半部分中选择出顶级智能体，并为后半部分绘制了性能。我们比较了针对该独立赌博机环境量身定制的几种算法，比较了整个回合的累积期望遗憾：Gittins指数(Gittins, 1979) (在有限水平情况下是贝叶斯最优)，UCB (Auer et al., 2002) (带有理论上的有限时间遗憾保证)和Thompson采样(Thompson, 1933) (在这种情况下渐近最优：参见Kaufmann et al., 2012b)。使用(Kaufmann et al., 2012a)的PymaBandits工具箱和自定义的Matlab脚本进行了模型仿真。

　　如图2a (绿线；"独立")所示，尽管元RL与Gittins(黑虚线)相比表现不佳，但其性能却优于Thimpson采样(灰色虚线)和UCB(浅灰色虚线)。为了验证向LSTM提供奖励信息的至关重要性，我们删除了此输入，而所有其他输入都保持不变。不出所料，所有赌博机任务的性能都处于偶然的水平。

 

3.1.2 BANDITS WITH DEPENDENT ARMS (I)

　　正如我们强调的那样，元RL的关键特性在于它产生了一种学习型RL算法，该算法在训练分布中利用了一致的结构。为了获得这一点的经验证据，我们从第一个实验中以更结构化的赌博机任务测试了智能体。具体而言，我们在双臂奖励分布相关的双臂赌博机上训练了该系统。在这种情况下，与上一节研究不同，一只臂的经验可提供另一只臂的信息。在这种设置下，标准的赌博机算法(包括UCB和Thompson采样)无法达到最优效果，因为它们并非旨在利用此类相关性。在某些情况下，可以为特定的臂结构量身定制算法(例如，参见Lattimore and Munos, 2014)，但通常需要针对特定​​问题进行广泛的分析。我们的方法旨在直接从目标赌博机领域的经验中学习与结构相关的赌博机算法。

　　我们考虑Bernoulli分布，其中两个臂的参数(p₁, p₂)在p₁ = 1 - p₂的意义上相关。我们考虑几种训练和测试分布。均匀是指p₁~U([0, 1]) (单位间隔内的均匀分布)。简单意味着p₁~U({0.1, 0.9}) (在这两个可能的值上均匀分布)，类似地，当p1~U({0.25, 0.75})时，我们称为中等；当p1~U({0.4, 0.6})时，我们称为困难。我们用D_u, D_e, D_m和D_h表示赌博机环境中的相应产生的分布。此外，我们还考虑了独立均匀分布(如上一节中的D_i所示)，其中p1, p2~U([0, 1])且独立。对智能体进行了有关赌博机环境的这五个分布的训练和测试(其中四个对应于相关分布：D_u, D_e, D_m和D_h；一个对应于独立案例：D_i)。作为对分配给任务分布(D_e, D_m, D_h)的名称的验证，结果表明，简单的任务比中等的任务更容易学习，而中等的任务比困难的任务更容易学习(图2f)。这与普遍的观点是一致的，即赌博机问题的困难程度与最优和次优臂的期望奖励之间的差值成反比。我们再次注意到，如预期的那样，不将奖励输入保留给LSTM，甚至在最简单的赌博机任务上也导致了偶然性能。

　　图2f报告了所有可能的训练测试方案的结果。通过观察累积期望遗憾，我们得出以下观察结果：i）在结构化环境(D_u, D_e, D_m和D_h)中受过训练的智能体开发了可以在结构化分布上进行测试时可以有效使用的先验知识——与Gittins的性能相当(图2c-f)，并且与在测试中所有结构化任务中接受独立臂(D_i)训练的智能体相比具有优势(图2f)。这是因为受过独立奖励(D_i)训练的智能体还没有学会利用在那些结构化任务中有用的奖励关联。ii）相反，当在独立分布上测试智能体时(D_i；图2f)，先前对任何结构化分布(D_u, D_e, D_m或D_h)的训练都会损害性能。这是有道理的，因为对依赖臂进行训练可能会产生依赖于特定奖励结构的策略，从而影响不存在此类结构的问题中的性能。iii）虽然先前的结果强调了元RL产生了一个单独的学习RL算法，该算法实现了先验依赖的赌博机策略，但结果也提供了证据，表明所遇到的确切训练分布范围之外还有一些泛化性(图2f)。例如，在分布更广泛的结构化分布(即D_u)上进行测试时，在分布D_e和D_m上受过训练的智能体表现良好。此外，我们的证据表明，从对较简单任务(D_e, D_m)的训练到对最难任务的测试(D_h；图2e)的推广，与对困难分布D_h本身的训练相比，具有相似甚至略胜一筹的性能(图2f)。相反，对困难分布D_h进行训练会导致对其他结构化分布(D_u, D_e, D_m)的泛化性较差，这表明仅对困难实例进行训练可能会导致学习的RL算法受到先验知识的限制更大，这可能是由于解决原始问题的困难性。

 

3.1.3 BANDITS WITH DEPENDENT ARMS (II)

　　在先前的实验中，该智能体可以利用学到的双臂之间的依赖关系胜过标准的赌博机算法。但是，它可以在始终选择自己认为是收入最高的臂的同时做到这一点。接下来，我们研究一个可以通过支付短期奖励成本来获取信息的问题。之前已经研究过类似的问题，这些挑战给标准的赌博机算法带来了挑战(参见例如Russo and Van Roy, 2014)。相比之下，人类和动物所做的决策牺牲了信息获取的即时奖励(例如Bromberg-Martin and Hikosaka, 2009)。
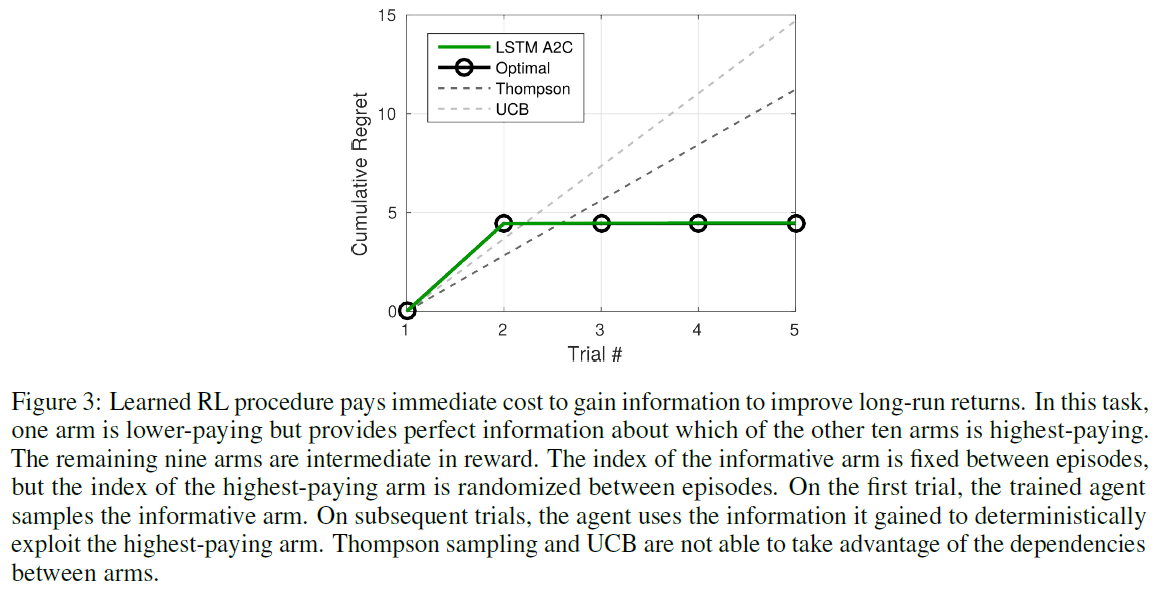
　　在此实验中，对智能体进行了11臂赌博机训练，臂之间有很强的依赖性。所有的臂都有确定的奖励。九个"非目标"臂的奖励=1，一个"目标"臂的奖励=5。同时，臂a₁₁始终是"信息性的"，因为目标臂的索引是a₁₁的奖励的10倍(例如，a₁₁上0.2的奖励表示a₂是目标臂)。因此，a₁₁的奖励范围是0.1到1。在每个回合中，目标臂的索引都是随机分配的。在每个回合的第一次试验中，智能体不知道目标是哪个臂，因此信息臂返回了期望奖励0.55，而每个目标臂都返回了期望奖励1.4。因此，选择信息臂意味着立即获得奖励，但要补偿价值信息。回合长五步。先前试验的奖励是作为对智能体的额外观察提供的。为了便于学习，它以one-hot格式编码。
　　结果如图3所示。尽管短期成本很高，但智能体一次学会了最优的长期策略，即对信息臂进行一次采样，然后使用所得信息来开发高价值目标臂。Thompson采样(如果提供了真实的先验信息)会搜索潜在的目标臂，并在找到目标后加以利用。UCB的性能较差，因为即使早期发现了目标臂，它也会对每个臂采样一次。

 

3.1.4 RESTLESS BANDITS

　　在先前的实验中，我们考虑了平稳性问题，即智能体的动作产生了关于任务参数的信息，这些任务参数在每个回合中都保持不变。接下来，我们考虑一个赌博机问题，其中奖励概率在一个回合的过程中发生变化，不同回合的变化率(波动率)不同。为了表现出色，智能体不仅必须跟踪最优臂，还必须推断回合的波动性并相应地调整其自身的学习率。在这样的环境中，当环境快速变化时，学习率应该更高，因为过去的信息变得越来越不相关(Behrens et al., 2007; Sutton and Barto, 1998)。
　　我们测试了元RL是否会使用具有奖励概率p₁和1-p₁的双臂Bernoulli赌博机任务来学习这种灵活的RL策略。p₁的值在"低波动"回合中缓慢变化，而在"高波动"回合中快速变化。智能体除了知道回合中的奖励历史之外，无法知道其处于哪种回合类型。图4a显示了示例"低波动"和"高波动"回合。奖励幅度固定为1，回合长100步。再次实现了UCB和Thompson采样以进行比较。UCB中的置信区间项的参数Χ设置为1，根据经验选择该参数是为了在我们的数据集上获得良好的性能。Thompson采样的后验更新包括对高斯随机游动的了解，但是所有回合的波动性都是固定的。

　　与之前的实验一样，与最优固定学习率(α=0.5)的Thompson采样，UCB或Rescorla-Wagner (R-W)学习规则(图4b；Rescorla et al., 1972)相比，元RL在测试中的遗憾率更低。为了测试智能体是否调整了有效学习率，以适应不同波动水平的环境，我们将R-W模型拟合到智能体的行为，将回合分为10个块，其中每个块仅由"低波动"或"高波动"组成回合。我们考虑了四个不同的模型，其中包含三个参数的不同组合：学习率α，softmax逆温度β和失效率ε，以解释与估计价值无关的无法解释的选择方差(Economides et al., 2015)。模型"b"仅包括β，"ab"包括α和β，"be"包括β和ε，以及"abe"包括所有三个。在10个回合的每个块中分别估计所有参数。在ε和α不自由的模型中，它们分别固定为0和0.5。根据贝叶斯信息准则(BIC)进行的模型比较表明，与每个块具有固定学习率的模型相比，对于每个块具有不同学习率的模型可以更好地描述元RL的行为。作为对照，我们对最优R-W智能体产生的行为进行了相同的模型比较，发现在每个回合中允许不同的学习率没有好处(模型"abe"和"ab" vs "be"和"b"；图4c -d)。在这些模型中，元RL行为的参数估计与回合的波动性密切相关，表明元RL将其学习率调整为回合的波动性，而拟合R-W行为的模型则简单地恢复了固定参数(图4e-f)。

 

3.2 MARKOV DECISION PROBLEMS

　　前面的实验着重于赌博机任务，其中的动作不会影响任务的基础状态。现在我们来谈谈动作确实会影响状态的MDP。我们从神经科学文献中得出的任务开始，然后转向最初是在动物学习的背景下研究的任务，该任务需要学习抽象的任务结构。与之前的实验一样，我们的重点是研究元RL如何适应任务结构的不变性。我们通过回顾最近在相关论文中报道的一个实验来总结(Mirowski et al., 2016)，该实验演示了元RL如何通过丰富的视觉输入来扩展到大规模导航任务。

 

3.2.1 THE “TWO-STEP TASK”

　　在这里，我们研究了在神经科学文献中广泛使用的一种环境中的元RL，以区分被视为支持决策制定的不同系统的贡献(Daw et al., 2005)。具体而言，开发此范式(被称为"两步任务"(Daw et al., 2011))是为了分解无模型的系统，该系统在状态中缓存动作价值(例如TD(1) Q学习；参见Sutton and Barto, 1998)，从有模型系统中学习环境的内部模型，并通过超前计划来评估决策制定时的动作价值(Daw et al., 2005)。我们的兴趣在于，尽管使用了无模型算法(在本例中为A2C)来训练系统权重，但元RL是否会引起模仿有模型策略的行为。

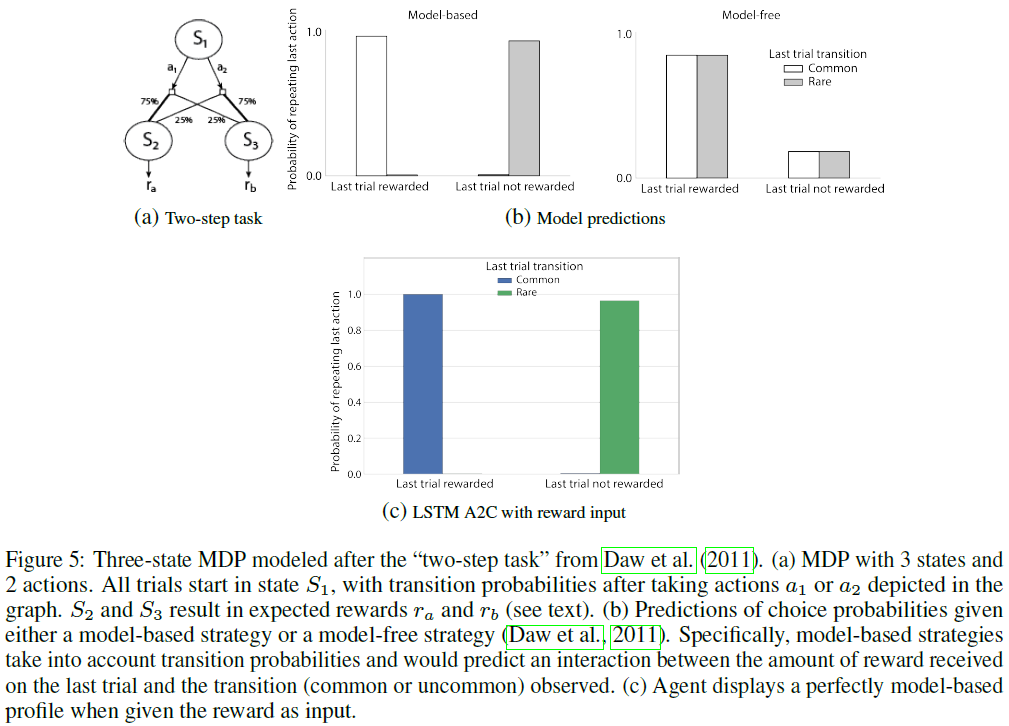
　　我们使用了两步任务的修改版，旨在增强有模型控制相比无模型控制的实用性(参阅Kool et al., 2016)。该任务的结构如图5a所示。从第一阶段状态S₁，动作a₁分别以概率0.75和0.25导致第二阶段状态S₂和S₃，而动作a₂以概率0.25和0.7导致S₂和S₃。一个第二阶段状态以0.9的概率给出的奖励为1.0(否则为零)。另一个以0.1的概率产生相同的奖励。为每个回合随机分配较高价值状态的标识。因此，两个第一阶段动作的期望价值为r_a = 0.9和r_b = 0.1，或者r_a = 0.1和r_b = 0.9。所有三个状态均由one-hot向量表征，并且转换模型在各个回合之间保持不变：即，只有第二阶段状态的期望价值在回合之间发生变化。
　　我们应用了神经科学文献中使用的常规分析方法，将无模型从有模型控制中分离出来(Daw et al., 2011)。这着重于"停留概率"，即在试验 t 处选择第二阶段奖励后，在试验t+1处选择第一阶段动作的概率，这取决于试验 t 是否涉及常见转换(例如，状态S₁处的动作a₁导致S₂)或罕见转换(状态S₁处的动作a₂导致S₃)。根据标准解释(参见Daw et al., 2011)，无模型控制(à la TD(1))预测应该有奖励的主要作用：如果跟随奖励，则第一阶段的动作往往会重复，而不管转换类型如何，如果后面跟着无奖励(图5b)，则此类动作往往不会重复(选择切换)。相反，有模型控制可预测奖励和转换类型之间的相互作用，从而反映出一种更加目标导向的策略，该策略将转换结构考虑在内。凭直觉，如果你在罕见的转换(例如，在状态S₁采取了动作a₂)之后获得了第二阶段的奖励(例如，在S₂处)，则根据你对转换结构的知识，可以最大程度地在下次试验中获得该奖励，最优的第一阶段动作是a₁(即转换)。

　　根据智能体的选择执行的停留概率分析结果显示出一种模式，该模式通常被解释为暗示有模型控制的操作(图5c)。与以前的实验一样，当奖励信息被保留在网络输入级别时，性能处于偶然级别。
　　如果按照神经科学中的标准实践进行解释，则该实验中模型的行为会反映出令人惊讶的效果：使用无模型RL进行训练会产生反映有模型控制的行为。我们必须注意到，对观察到的行为模式有不同的解释(Akam et al., 2015)，我们将在下面返回这一点。但是，尽管有此注意事项，但本实验的结果进一步说明了从元RL出现的学习过程可能与用于训练网络权重的原始RL算法完全不同，并采取一种利用一致的任务结构的形式。

 

3.2.2 LEARNING ABSTRACT TASK STRUCTURE

　　在我们进行的最终实验中，我们通过研究一项涉及丰富的视觉输入，更长的时间范围和稀疏奖励的任务，朝着检验元RL的可扩展性迈出了一步。另外，在本实验中，我们研究了一种元学习任务，该任务要求系统调整为抽象的任务结构，其中一系列对象扮演系统必须推断的定义角色。
　　该任务改编自Harlow (1949)对动物行为进行的经典研究。在执行原始任务的每次试验中，Harlow都向猴子展示了两个带有视觉对比的物体。其中一个覆盖装有食物的井。另一个覆盖空井。动物在两个物体之间自由选择，并且如果存在食物的话可以获取该奖励。阶段然后被隐藏，并随机重置对象的左-右位置。然后开始了新的试验，动物再次自由选择。对于两个相同的物体，此过程继续进行了一定数量的试验。在完成这组试验后，用两个全新且不熟悉的物体替换了原来的两个物体，然后重新开始了该过程。重要的是，在每个试验阶段中，选择一个物体要始终如一地获得奖励(无论其左-右位置如何)，而另一个物体始终没有得到奖励。Harlow (Harlow, 1949)观察到，经过大量练习，猴子表现出的行为反映出对任务规则的理解。当展示两个新物体时，猴子在它们之间的第一选择必然是任意的。但是，在观察到这种第一选择的结果之后，猴子便总是选择有奖励的物体。

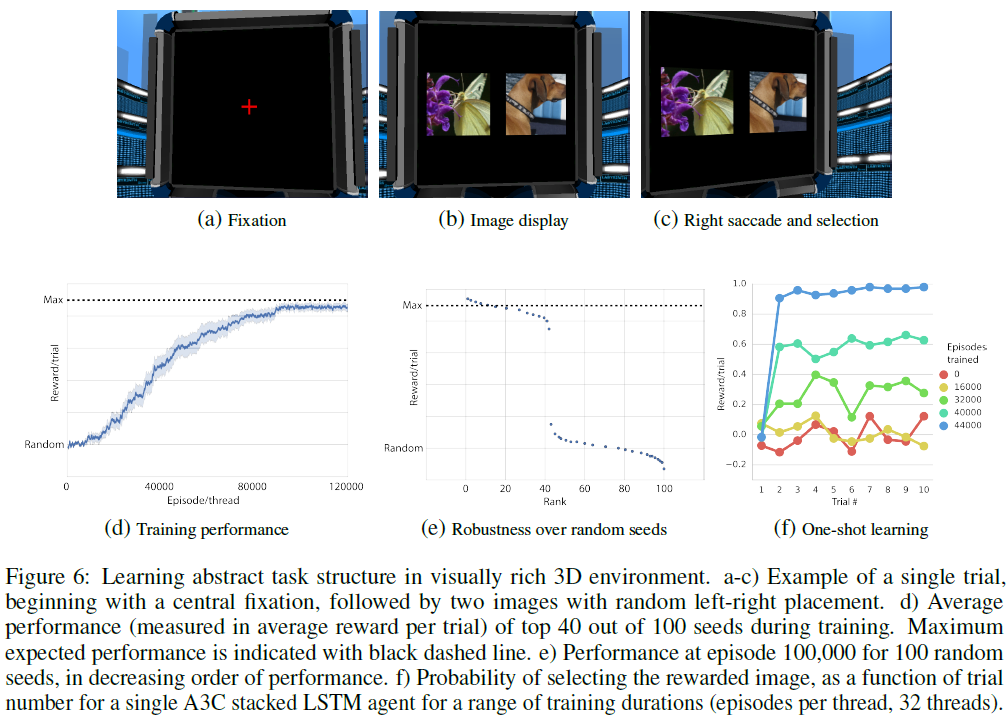
　　我们预期元RL应该引起相同的抽象one-hot学习模式。为了对此进行测试，我们将Harlow的范例调整为视觉固定任务，如下所示。一个84x84像素的输入代表一个模拟的计算机屏幕(参见图6a-c)。在每个试验开始时，该显示为空白，除了一个小的中央固定叉(红色十字准线)。智能体选择了离散的左-右动作，这些动作在相应的方向上将其视线移动了约4.4度，并且动量效应较小(或者，可以选择无操作动作)。要完成试验，需要执行两项任务：扫描到中央注视交叉点，然后扫描到正确的图像。如果智能体将注视交叉点保持在视场中心(视角范围为3.5度以内)至少四个时间步骤，则得到的奖励为0.2。然后，固定十字消失，在显示器的左侧和右侧分别出现了两个图像——从ImageNet数据集中随机抽取(Deng et al., 2009)并调整为34x34大小(图6b)。然后，智能体的任务是通过旋转直到图像的中心与视场的中心对齐(在7度视角范围内)来“选择”其中一幅图像。一旦选择了其中一张图像，两张图像都消失了，在10个时间步骤的间隔之后，重新出现了固定十字，开始了下一次试验。每个回合最多包含10个试验或3600个步骤。参考Mirowski et al. (2016)，我们将动作重复次数设为4，这意味着在完成注视后，选择一张图片至少要进行三个独立的决定(12个原始动作)。但是，应当注意的是，智能体的旋转位置不受限制。也就是说，可能会发生360度旋转，而模拟的计算机屏幕只能对向65度。

　　尽管在每个回合的开头选择了新的ImageNet图像(从一组1000张图像中进行替换采样)，但是在一个回合内的所有试验中都重复使用了相同的图像，尽管其左-右位置随机变化，类似于Harlow的实验中的物体。就像在那个实验中一样，在整个回合中，任意选择一张图像作为"奖励"图像。选择此图像产生的奖励为1.0，而另一个图像产生的奖励为-1.0。在测试过程中，将A3C学习率设置为零，并从单独的1000个不受支持的集合中抽取ImageNet图像，这些图像在训练过程中从未出现过。

　　对最优超参数进行了网格搜索。在完美的性能下，智能体可以每20-30个步骤完成一个试验，并获得每10个试验9个的最大期望奖励。鉴于任务的性质——它需要one-shot图像奖励记忆以及在相对较长的时间范围内保持此信息(即，通过固定注视，交叉选择和跨试验)——我们不仅评估了卷积LSTM的性能，接收奖励和动作作为额外输入的架构(参见图1b和表1)，以及在下面讨论的导​​航任务中使用的卷积堆栈LSTM架构(参见图1c)。

　　智能体性能如图6d-f所示。尽管单个LSTM智能体在解决任务方面相对成功，但堆栈LSTM变体表现出了更好的鲁棒性。也就是说，最优超参数集的随机种子的43％在上限执行(图6e)，而单个LSTM的26％。
　　就像Harlow的实验中的猴子(Harlow, 1949)一样，网络融合在一个最优策略上：不仅智能体成功地注视着开始每个试验，而且从每个回合的第二次试验开始，它总是选择奖励图像，无论它在第一次试验中选择了哪个图像(图6f)。这反映了一种令人印象深刻的one-shot学习形式，它反映了对任务结构的内在理解：在观察到一个试验结果后，智能体将复杂且陌生的图像绑定到特定的任务角色。
　　在其他地方报道的进一步实验(Wang et al., 2017)证实了相同的循环A3C系统也能够解决难度更大的任务。在此任务中，仅一个图像(这被随机指定为将要选择的奖励物品或应避免的不奖励物品)在一个回合中的每个试验中被呈现，而在每个试验中呈现的另一幅图像则是新颖的。

 

3.2.3 ONE-SHOT NAVIGATION

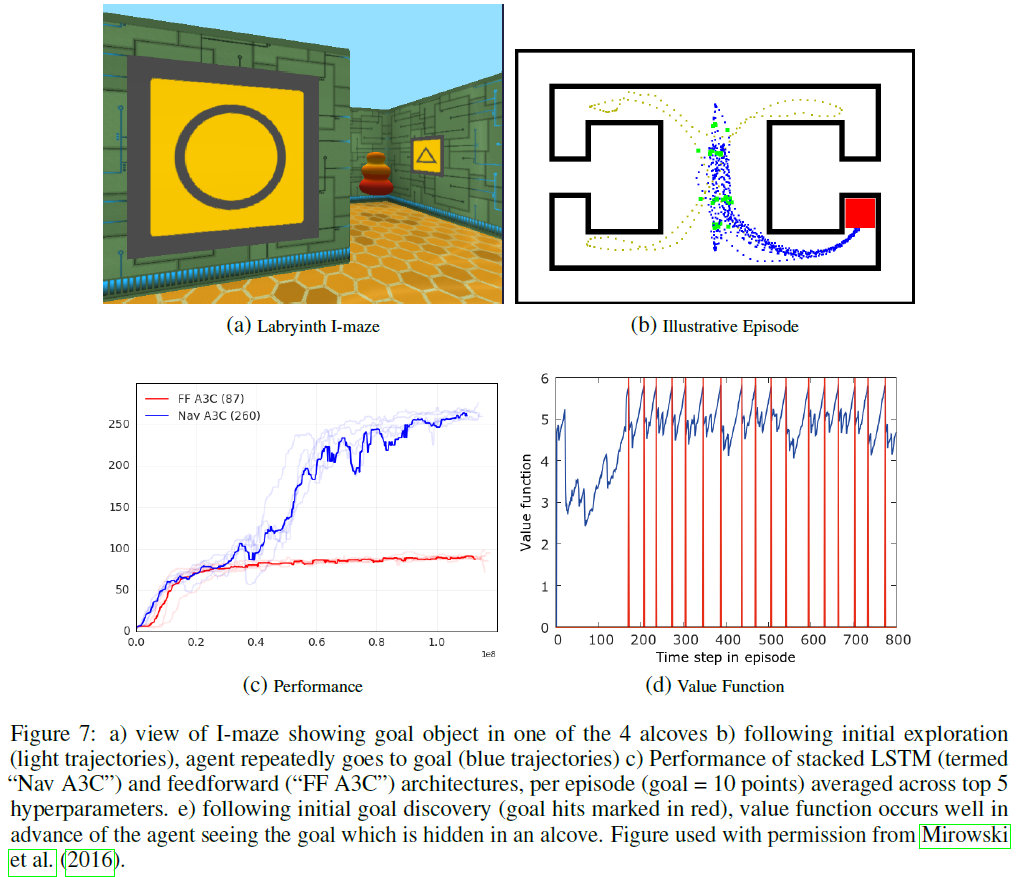
　　使用Harlow任务的实验证明了元RL在相对较长的时间范围内，在视觉丰富的环境中有效操作的能力。在这里，我们考虑了导航领域内最近报道的相关实验(Mirowski et al., 2016) (另请参见Jaderberg et al., 2016)，并讨论了如何将这些实验改写为元RL的示例——证明了该原理在更典型的MDP设置上的可扩展性，由于动态变化的稀疏奖励而造成了具有挑战性的RL问题。

　　具体来说，我们考虑的环境是固定的，但目标在每个回合中随机更改位置(图7；Mirowski et al., 2016)。尽管布局相对简单，但迷宫环境(详细信息参见Mirowski et al., 2016)更加丰富且离散化程度更高(参见VizDoom)，从而导致了长时间范围；训练好的智能体需要大约100步(10秒)才能在给定回合中首次达到目标。结果表明，堆栈LSTM架构(图1c)可以接收与我们的Harlow实验中等效的奖励和动作当做额外的输入，从而实现了接近最优的行为——在初始探索期之后，对目标位置显示了one-shot记忆，随后是反复开发(见图7c)。与随后的访问(约30个时间步骤)相比，首次达到目标(约100个时间步骤)的时延大大减少，这证明了这一点。值得注意的是，仅接收单个图像作为观察结果的前馈网络(参见图7c)无法解决任务(即，连续目标奖励之间的时延没有减少)。尽管在Mirowski et al. (2016)中没有这样解释，这清楚地证明了元RL的有效性：通过使用固定且更多增量的RL算法(即策略梯度)进行训练，出现了具有one-shot学习能力的单独的RL算法。可以将元RL视为允许智能体在初始探索之后推断最优价值函数(请参见图7d)—— 额外的LSTM向LSTM提供有关当前相关目标位置的信息，该LSTM在回合的扩展时间范围内输出策略。综上所述，元RL允许基本的无模型RL算法解决具有挑战性的RL问题，否则可能需要根本不同的方法(例如，基于后继表征或完全有模型的RL)。

 

4 RELATED WORK

　　我们已经谈到了深度元RL与Hochreiter et al. (2001)的开创性工作之间的关系。使用循环网络在完全监督的情况下进行元学习(另见Cotter and Conwell, 1990; Prokhorov et al., 2002; Younger et al., 1999)。Santoro et al. (2016)最近扩展了该方法，展示了利用外部记忆结构的实用性。Schmidhuber et al. (1996)先前曾讨论过将元学习与RL相结合的想法。这项工作似乎引入了"元RL"一词，与我们的工作有所不同，因为它不涉及神经网络的实现。但是最近，人们对使用神经网络学习优化程序，使用一系列创新的元学习技术的兴趣激增(Andrychowicz et al., 2016; Chen et al., 2016; Li and Malik, 2016; Zoph and Le, 2016)。Chen et al. (2016)的最新工作在想法上与我们在这里提出的工作特别接近，可以被视为使用与我们所追求的大致相似的元学习策略来处理“无限赌博机”的情况。

　　本研究还与尚未进行元学习框架的近期工作的不同机构有着密切的关系。大量研究已使用深度RL来训练导航任务上的RNN，其中任务的结构(例如目标位置或迷宫配置)随回合的不同而有所不同(Jaderberg et al., 2016; Mirowski et al., 2016)。我们上面提出的最终实验(例如，Mirowski et al., 2016)就是一个例子。在某种程度上来说，此类实验涉及深度元RL的关键成分——带有记忆的神经网络，通过RL在一系列相互关联的任务上进行训练——几乎可以肯定，这些实验都涉及了我们目前所描述的元学习 工作。这项相关的工作表明，与我们自己的实验相比，元RL可以有效地应用于更大范围的问题。重要的是，这表明扩展该方法的关键因素可能是将记忆机制纳入非结构化RNN固有的记忆机制之外(见Graves et al., 2016; Mirowski et al., 2016; Santoro et al., 2016; Weston et al., 2014)。就我们而言，我们的工作表明，深度循环RL智能体有潜能来元学习任务结构的非常抽象的方面，并发现将这种结构用于快速且灵活适应的策略。

　　在完成本研究期间，Duan et al. (2016)报告了密切相关的工作。与我们一样，Duan和同事使用深度RL来训练循环网络进行一系列相互关联的任务，结果是网络动态学习了第二个RL程序，该过程的运行时间比原始算法快。他们将这些学习过程的性能与传统RL算法在多个领域的性能进行了比较，包括赌博机和导航。这项并行工作与我们自己的工作之间的重要区别是，前者主要关注相对非结构化的任务分布(例如，均匀分布的赌博机问题和随机MDP)；相反，我们的主要兴趣在于结构化的任务分布(例如，依赖赌博机和Harlow, 1949引入的任务)，因为正是在这种情况下，系统可以学习有偏的(因此有效)利用常规任务结构的RL程序。在这方面，这两种观点是相辅相成的。

 

5 CONCLUSION

　　AI当前面临的挑战是设计智能体，以通过利用从先前经验中获得的相关知识来快速适应新任务。在当前的工作中，我们报告了对我们认为是实现该目标的一种有希望途径的初步探索。深度元RL包含三个要素的组合：(1) 使用深度RL算法训练RNN，(2) 包括一系列相互关联任务的训练集，(3) 网络输入，包括选择的动作和在上一个时间间隔中收到的奖励。关键的结果是从设置中自然而然地产生出来的，而不是经过专门设计的，其结果是，循环网络动态学会了实现第二个RL程序，该程序独立并且可能与用于训练网络权重的算法非常不同。至关重要的是，将这种学习过的RL算法调整为训练任务的共享结构。从这个意义上讲，学习型算法建立在适合于域的偏差中，这可以使其比通用算法有更高的效率。这种偏差效果在我们涉及依赖赌博机的实验结果中特别明显(第3.1.2和3.1.3节)，在这种情况下，系统学会了利用任务的协方差结构；在我们对Harlow的动物学习任务的研究(第3.2.2节)中，循环网络学会了利用任务的结构来展示具有复杂新颖刺激的one-shot学习。

　　我们的一项实验(第3.2.1节)说明了一点，即使用无模型RL算法训练的系统可以开发出模仿有模型控制的行为。对此结果还需进一步评论。正如我们对模拟结果的介绍所指出的那样，在认知和神经科学文献中，网络所显示的选择行为模式已反映出有模型控制或树搜索。然而，正如最近的工作所提到的，具有适当状态表征的无模型系统可能会产生相同的模式(Akam et al., 2015)。确实，我们怀疑这实际上是我们网络的操作方式。但是，其他发现表明，当在一组更多样化的任务上训练相似的系统时，可以出现更明确的有模型控制机制。特别是，Ilin et al. (2007)表明，在随机迷宫上训练的循环网络可以近似动态编程程序(另请参见Silver et al., 2017; Tamar et al., 2016)。同时，正如我们所强调的，我们认为深度元RL的一个重要方面是它产生了一个学习型RL算法，该算法利用了任务结构的不变性。作为结果，当面对千差万别但仍然结构化的环境时，深度元RL似乎会生成RL过程，该过程占据了无模型RL与有模型RL之间的灰色区域。

　　在3.2.1节中研究的两步决策问题来自神经科学，我们认为深度元RL在该领域可能具有重要意义(Wang et al., 2017)。元RL的概念先前已在神经科学中进行过讨论，但仅在狭义上进行了讨论，据此，元学习可调整标量超参数，例如学习率或softmax逆温度(Khamassi et al., 2011; 2013; Kobayashi et al., 2009; Lee and Wang, 2009; Schweighofer and Doya, 2003; Soltani et al., 2006)。在最近的工作中(Wang et al., 2017)，我们表明深度元RL可以解释更广泛的实验观察结果，为理解多巴胺和前额叶皮层在生物学RL中的各自作用提供了一个综合框架。