Revisiting Fundamentals of Experience Replay

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

ICML 2020

Abstract

　　经验回放对于深度RL中的异策算法至关重要，但是在我们的理解上仍然存在很大差距。因此，我们对Q学习方法中的经验回放进行了系统且广泛的分析，重点是两个基本属性：回放容量和学习更新与所收集经验的比率(回放率)。我们的加性和消融研究颠覆了有关经验回放的传统观点——更大的容量被发现可以显著提高某些算法的性能，而不会影响其他算法。与直觉相反，我们表明，理论上没有根据且未经校正的n步回报是唯一有益的，而其他技术则对于通过更大的内存进行筛选提供了有限的好处。另外，通过直接控制回放率，我们可以结合文献中的先前观察结果，并通过经验来衡量其在三种深度RL算法中的重要性。最后，我们通过测试关于这些性能优势的性质的一组假设来得出结论。

1. Introduction

　　经验回放是异策深度RL中的基本数据生成机制(Lin, 1992)。通过存储固定数量的最新转换样本进行训练，可以提高样本效率和稳定性。但是，经验回放与现代算法组件之间的交互作用仍然知之甚少。这种缺乏理解阻碍了进展，因为如果不进行大量调整，研究人员将无法衡量算法变更的全部影响。因此，我们提出了一项大规模研究，以了解学习算法和数据生成机制之间的交互，从而为更好的算法设计提供依据。
　　研究回放缓存的早期工作通常专注于单个超参数，例如回放缓存的容量(Zhang＆Sutton, 2017)，自Mnih et al. (2013)在该领域的开创性工作以来通常被保留。我们首先确定几个这样的超参数(例如缓存容量和数据吞吐率)以相互联系的方式影响经验回放，从而修改了可用于智能体的数据量和该数据的典型年龄。这激发了一套全面的实验，以了解独立修改每个属性的相对效果。然后，我们做出令人惊讶的发现，即这些影响主要取决于特定算法组件(n步回报)的存在，而n步回报以前未与经验回放相关联。最后，我们通过研究几种假设来揭示为什么存在这种联系。

2. Background

2.1. Deep reinforcement learning

　　近年来，深度RL领域已寻求将上述经典RL算法与机器学习中的现代技术相结合，以获得可扩展的学习算法。深度Q网络(DQN)(Mnih et al., 2015)将Q学习与神经网络函数近似和经验回放相结合(Lin, 1992)，以产生可扩展的RL算法，该算法在Arcade学习环境(Bellemare et al., 2013)中的一系列游戏中实现超出人类的性能。从那以后，已经开发出许多其他方法，它们可以像DQN一样被理解为包括三个基本单元：

函数近似架构；
学习算法；
生成训练数据的机制。

　　自从引入原始DQN算法以来，在这三个领域都进行了一系列创新。其中有限的选择包括基于对偶结构(Wang et al., 2015)和各种形式的复现(Hausknecht＆Stone, 2015；Kapturowski et al., 2019)，使用辅助任务的学习算法(Jaderberg et al., 2016；Fedus et al., 2019)，RL的分布变体(Bellemare et al., 2017；Dabney et al., 2018)以及在经验回放中使用优先采样(Schaul et al., 2015)。
　　结合了几种此类创新的著名智能体是Rainbow (Hessel et al., 2018)。Dopamine (Castro et al., 2018)中提供了基于该智能体的开源实现，与原始DQN智能体相比有四个主要区别：

优先经验回放(PER)(Schaul et al., 2015)：一种从回放缓存非均匀采样的方案，该方案偏向具有高TD误差的转换。相反，DQN从回放缓存中均匀采样经验。
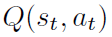n步回报：不是根据单步TD误差来训练动作-价值估计Q(s_t, a_t)，而是使用n步目标，并根据行为策略μ生成中间动作。
Adam优化器(Kingma＆Ba, 2014)：一种改进的一阶梯度优化器，可对第一和第二梯度矩进行归一化，与DQN使用的RMSProp优化器相反。
C51 (Bellemare et al., 2017)：一种分布RL算法，该算法训练一个智能体对可能的未来回报的分布进行一系列预测，而不是仅仅估计标量期望回报。

　　Dopamine Rainbow智能体与Hessel et al. (2018)的区别在于，前者不包括双重DQN更新(Van Hasselt et al., 2016)，对偶结构(Wang et al., 2015)或带噪网络(Fortunato et al., 2018)。为了完整起见，我们在附录中对这些算法调整的精确细节进行了深入的讨论。

2.2. Experience replay

　　DQN类型算法的关键组成部分是经验回放(Lin, 1992)。经验回放是一个固定大小的缓存，其中包含策略收集的最新转换。通过使数据可以在训练中多次重用，而不是在收集后立即丢弃数据，这可以大大提高算法的采样效率。
　　经验回放通常实现为循环缓存，其中缓存中最旧的转换将被删除，以便为刚刚收集的转换腾出空间。从缓存中以固定的间隔对转换进行采样，以用于训练。最基本的采样策略是均匀采样，其中缓存中的每个转换都以相等的概率被采样。可以使用其他采样策略，例如优先经验回放(Schaul et al., 2015)来代替均匀采样。虽然这是最常见的实现，但可以使用其他变体，例如分布经验回放缓存(Horgan et al., 2018)。
　　Mnih et al. (2015)将经验回放大小设置为可容纳1M个转换。通常在DQN之外的工作中保留此设置(Hessel et al., 2018)。在这项工作中，我们固定了算法的其他组件，并研究了修改经验回放各个方面的效果。

2.3. Related work

　　尽管第2.1节中列出的基于DQN的智能体的三个主要方面已受到了很多关注，但在这些领域中研究设计选择之间的交互方面却花了很少的精力。值得注意的例子包括原始的Rainbow工作(Hessel et al., 2018)，以及更专注于λ-回报和回放的最新作品(Daley＆Amato, 2019)。这项工作的主要目的是通过经验回放和学习算法的形式，增进我们对数据生成机制之间关系的理解。

　　Zhang＆Sutton (2017)研究了回放缓存大小对复杂程度不同的智能体的性能的影响，注意到回放缓存的超参数通常未被很好地理解，部分原因是现代学习系统的复杂性。他们发现，较小的回放缓存和较大的回放缓存都不利于一组三个任务的性能：Gridworld，LUNAR LANDER (Catto, 2011)和Arcade学习环境的PONG (Bellemare et al., 2013)。Fu et al. (2019)报告说，智能体程序的性能对每个梯度步骤所采取的环境步骤数很敏感，比率太小或太大也会影响性能。van Hasselt et al. (2019)结合批大小更改此比率，以获得更高样本效率的Rainbow版本。除了直接操作缓存的这些属性外，其他工作还集中在从回放采样的替代方案上(Pan et al., 2018；Schlegel et al., 2019)。

3. Disentangling experience replay

　　我们对回放中存在的数据类型影响学习的方式进行了详细研究。在更早的工作中，Zhang＆Sutton (2017)研究了增加DQN回放缓存大小的影响。我们注意到，除了随时增加可用于智能体的样本多样性之外，较大的回放缓存通常还包含更多的异策数据，因为来自较旧策略的数据在缓存中保留的时间更长。当我们改变数据进入和离开缓存的频率时，智能体的行为是另一个需要理解的变化因素，因为这在分布智能体(例如R2D2 (Kapturowski et al., 2019))中经常被利用。我们的目标是尽可能地消除这些单独的方式。为了使这些想法更精确，我们首先介绍一些我们可能希望隔离的回放属性的正式定义，以便更好地理解回放与学习的交互。

3.1. Independent factors of control

　　我们首先解开修改缓存大小时受影响的两个属性。

Definition 1. 回放容量是缓存中存储的转换总数。

　　根据定义，当缓存大小增加时，回放容量也会增加。较大的回放容量通常会导致较大的状态-动作范围。例如，ε-贪婪策略以概率ε随机采样动作，因此容量为N的回放缓存中的期望随机动作总数将为εN。

Definition 2. 回放中存储的转换年龄定义为自生成转换以来学习者所采取的梯度步骤数。回放缓存中代表最旧策略年龄的是缓存中最旧转换年龄。

　　缓存大小直接影响最旧策略年龄。可以粗略地将该量视为缓存中转换的异策性程度的代理。从直觉上讲，策略越旧，与当前策略的差异就越大。但是，请注意，这种直觉并不适用于所有情况。例如，如果通过一个策略的小集合来执行策略循环。

　　每当回放缓存大小增加时，回放容量和最旧策略年龄都会增加，并且这两个独立因素之间的关系可以用另一个量(回放率)来捕获。

Definition 3. 回放率是每个环境转换的梯度更新数。

　　回放率可以看作是智能体在现有数据上学习与获得新经验之间相对频率的度量。当缓存大小增加时，回放率保持恒定，因为回放容量和最旧策略年龄都增加了。但是，如果两个因素之一被独立调节，则回放率将改变。特别是，当最旧策略保持固定时，增加回放容量需要每个策略进行更多转换，从而降低了回放率。当回放容量保持固定时，减少最旧策略年龄会要求每个策略进行更多转换，这也会降低回放率。
　　在(Mnih et al., 2013)中建立的超参数中，每收集4个环境步骤都会更新一次策略，因此回放率为0.25。因此，对于1M个转换的回放容量，回放缓存中捕获的最旧策略年龄为250k梯度更新。图1计算回放容量或最旧策略年龄时的结果回放率。在最近有关深度RL方法的几项研究中，与回放率相似的量也被认为是重要的超参数(Wang et al., 2016；Kapturowski et al., 2019；Hamrick et al., 2020；Lin＆Zhou, 2020)。

3.2. Experiments

　　我们在常用的Atari ALE环境(Bellemare et al., 2013)上进行具有粘性动作的实验(Machado et al., 2018)。为了减轻实验的计算负担，我们专注于14个游戏的子集，因为我们的目标是为这两个因素确定一个相当大的价值网格。选择子集的方式应能反映游戏中环境的多样性(例如，确保我们拥有稀疏且艰苦的探索游戏，例如蒙特祖玛的复仇)。对于每个游戏，我们运行3个不同的随机种子。在本研究中，我们使用在Dopamine (Castro et al., 2018)中实现的Rainbow (Hessel et al., 2018)作为我们的基础算法，因为它在现有Q学习智能体中表现出色。

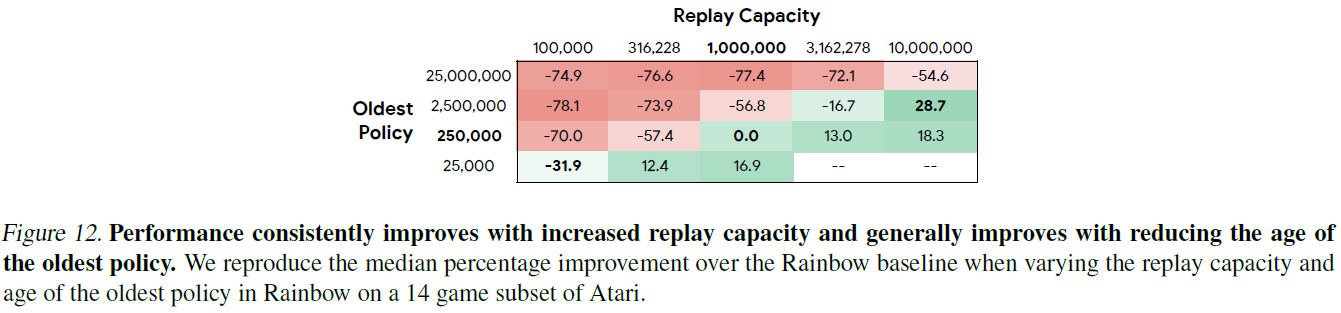
　　在这些实验中，我们将梯度更新的总数和每个梯度更新的批大小固定为Rainbow使用的设置，这意味着所有智能体都在相同数量的总转换上训练，尽管由于控制回放中最旧的策略。Rainbow使用的回放容量为1M，最旧策略为250k，对应的回放率为0.25。我们评估了5个回放容量设置(从0.1M到10M)和4个最旧策略(从25k到25M)的组合，但是排除了回放率最低的两个设置，因为它们在计算上不切实际，因为每个策略要求大量转换。每个设置的回放率如图1所示，Rainbow的结果如图2所示。有几种趋势是显而易见的：

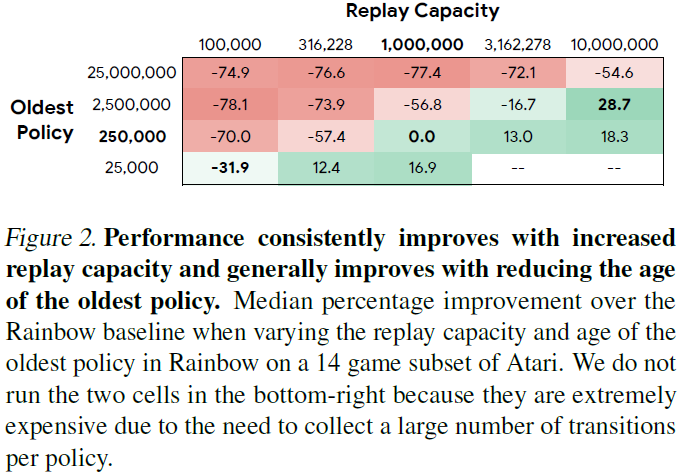
Increasing replay capacity improves performance. 在固定最旧策略时，性能会随着回放容量的增加而提高(图2中的行)。尽管改进的幅度取决于最旧策略的设置，但不管最旧策略的具体价值如何，这种总体趋势都将保持不变。可能较大的回放容量由于具有较大的状态-动作范围而改进了价值函数估计，这可以降低过拟合到一小部分状态-动作的机会。

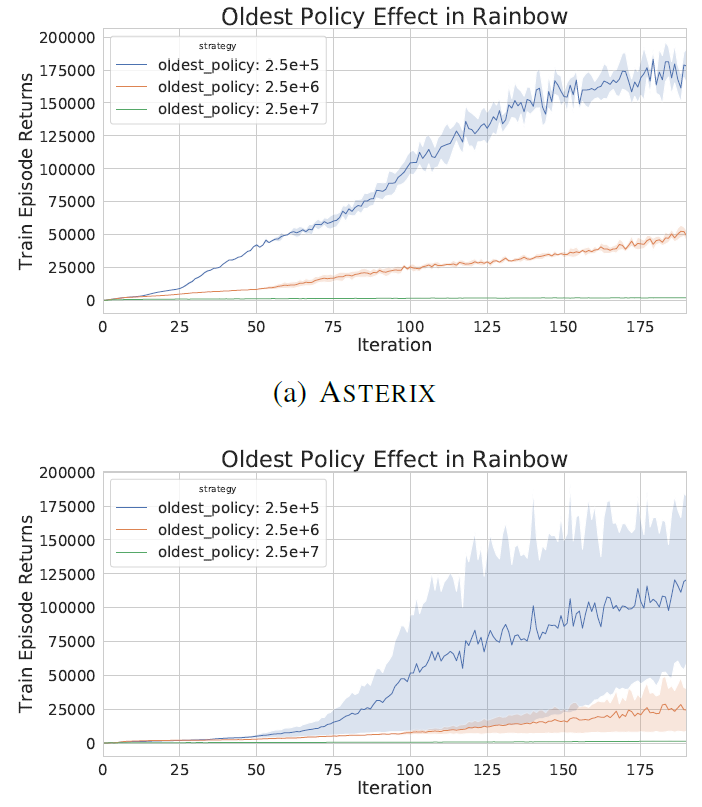
Reducing the oldest policy improves performance. 确定回放容量时，性能会随着最旧策略年龄的减少而提高(图2中的列)。我们将图3中三个游戏的三个设置的训练曲线可视化。使用启发式策略，即最旧策略年龄可以代表异策性，这一结果表明，从更多同策数据中学习可以提高性能。随着智能体在训练过程中不断进步，它会在环境的更高质量(以回报衡量)上花费更多的时间。学习更好地估计高质量区域的回报可以带来更多收益。

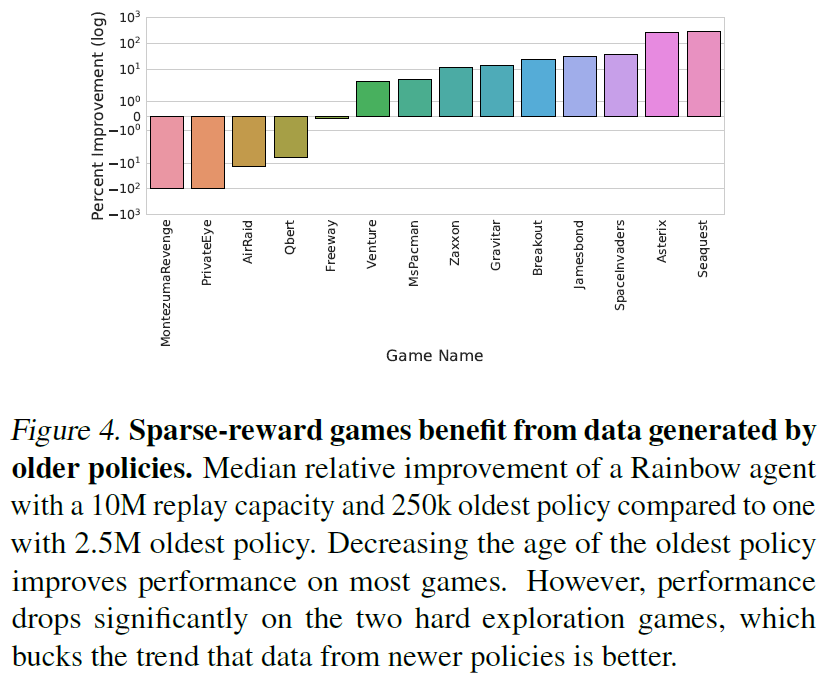
　　但是，这种趋势的例外情况是在10M回放容量设置中，当年龄从2.5M转到250k时性能会下降。这种畸变是由两个特定游戏的得分下降(参见图4)来解释的，蒙特祖玛的复仇和PRIVATEEYE被认为是稀疏奖励的艰苦探索环境(Bellemare et al., 2016)。仅从最新策略中采样的智能体似乎无法找到稀疏的奖励(参见图3(c))。

Increasing buffer size with a fixed replay ratio has varying improvements. 如果在修改缓存大小的同时将回放率固定，则由于增加回放容量而导致的改进与因缓存中具有较旧的策略而导致的退化之间存在相互作用。两种影响的大小取决于这些数量的特定设置。通常，随着最旧策略年龄的增加，增加回放容量所带来的收益并不那么大。

3.3. Generalizing to other agents

　　前面小节中的实验是使用Dopamine Rainbow算法进行的，但是我们现在测试经验回放在其他Q学习变体中是否表现出相似的行为。特别是，我们测试回放容量的增加是否可以使用原始DQN算法提高性能(Mnih et al., 2015)。
　　我们维护专门针对DQN调整的默认Dopamine超参数(Castro et al., 2018)，并将回放容量从1M增加到10M。我们考虑两个实验变体：固定回放率或最旧策略。固定回放率对应于增加缓存大小超参数的标准设置。固定最旧策略需要调整回放率，以便回放缓存始终包含一定数量的梯度更新内的策略。结果列于表1。

　　出乎意料的是，为DQN智能体提供更大数量级的内存，无论回放率或最旧策略是否固定，都无济于事。这些结果与Rainbow智能体的动态形成鲜明对比，后者的动态性能不断提高，回放容量也得到了不断的提高。我们还注意到，固定的回放率结果与Zhang＆Sutton (2017)的结论不同，即较大的回放容量是有害的——相反，我们观察到没有实质性的性能变化。
　　这个结果令人质疑，这两种基于价值的算法之间的差异正在推动对增加回放缓存大小的独特响应。在下一部分中，我们将进行大规模研究，以确定哪些算法组件可使Rainbow利用更大的回放容量。

4. What components enable improving with a larger replay capacity?

　　如第2.1节所述，Dopamine Rainbow智能体是DQN智能体，具有四个额外组件：优先经验回放(Schaul et al., 2015)，n步回报，Adam (Kingma & Ba, 2014)和C51 (Bellemare et al., 2017)。因此，我们试图将较大回放容量下的性能差异归因于这四个组件中的一个或多个。为此，我们尝试使用组件的不同子集，并测量增加回放容量时此变体是否有所改进。在这些研究中，我们专门测量了增加回放容量后的相对改进，而不是哪个变体获得了最高的绝对回报。

4.1. Additive and ablative experiments

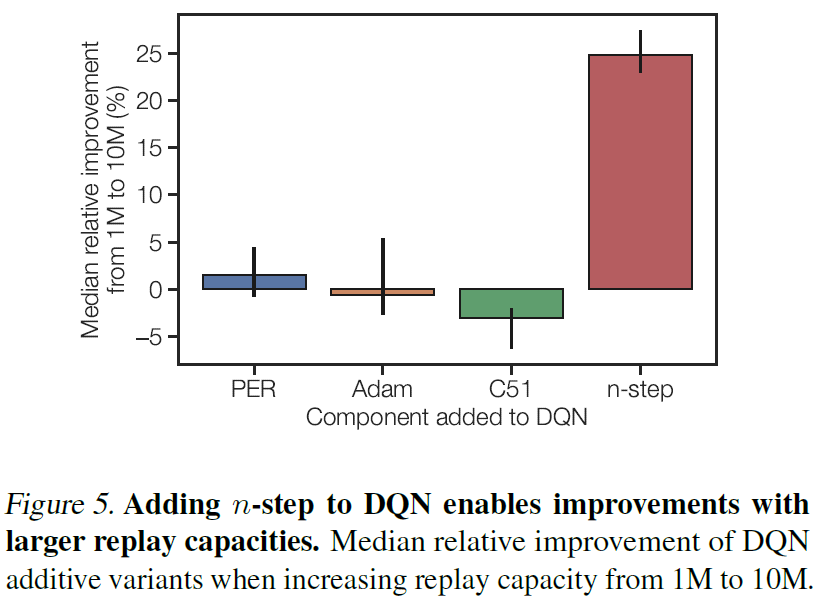
　　我们从加性研究开始，在该研究中，将Rainbow的单个组件添加到DQN算法中，从而导致四个智能体变量。当每个变体的回放容量从1M增加到10M时，我们独立地计算相对性能差异。当增加回放容量时，我们将固定回放率，并在本节后面的部分重新讨论固定最旧策略的情况。我们评估了20种游戏，这是上一节中使用的14种游戏的超集。结果如图5所示。
　　可以通过更大的回放容量来显著改进的唯一加性变体是具有n步回报的DQN智能体。据此，我们假设n步回报独特地带来了更大回放容量的收益。作为对该假设的检验，从Rainbow智能体中删除n步回报应该抑制这种消融变体以更大的回放容量得到改进。此外，要使n步回报成为唯一有影响力的组件，其他三个组件(PER，Adam，C51)的消融版本必须仍具有较大的回放容量，以显示改进。我们在图6中显示了这个消融的Rainbow实验的结果。

　　如预期的那样，剥离了n步回报的Rainbow智能体无法从更大的回放容量中受益，而剥离了其他组件的Rainbow智能体仍然可以改进。这些结果表明，n步回报对于确定Q学习算法是否可以通过更大的回放容量来提高至关重要。另一个令人惊讶的发现是，优先经验回放不会显著影响具有较大内存的智能体的性能。凭直觉，随着回放缓存大小的增长，可能期望优先经验回放对于向学习者提供相关经验很有用，结果表明并非如此。附录B中提供了每个游戏级别的详细信息。

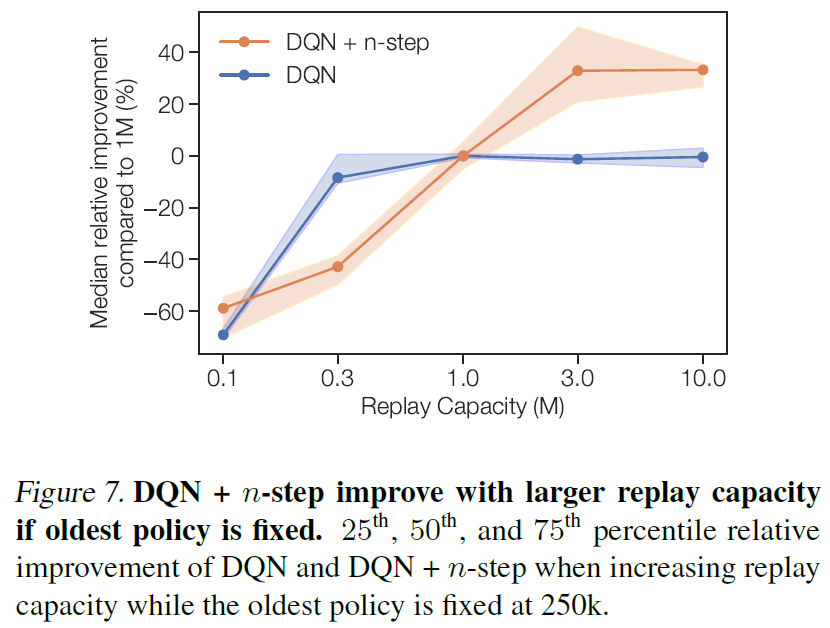
　　作为一项最终控制措施，如果最旧的策略保持不变，而不是使回放率保持不变，则我们检查具有n步回报的DQN是否仍会随着较大的回放容量而提高。图7显示，当从高度调节的默认值1M增加回放容量时，DQN + n步算法能够持续改进，而标准DQN则不能。如果给定的数据较少，则具有n步的DQN的性能可能会更差，这一点我们将在5.2节中进行回顾。
　　综上，这些结果表明，n步是利用更大的回放大小的关键因素。这是意外的。从理论上讲，未经修正的n步回报无法用于异策数据，因为它们无法修正策略差异，但由于方便和经验优势，这仍可以使用。实验表明，将这种理论上没有原则的方法扩展到可能进一步加剧问题的机制¹对于性能至关重要。

¹在固定回放率下的较大缓存将包含来自较旧策略的数据，这可能会增加旧行为与当前智能体之间的差异。

4.2. n-step for massive replay capacities

　　这些结果表明，增加回放容量时应使用n步回报。但是，我们以前的结果仅考虑了回放容量最高为1000万，这是整个训练过程中收集的2亿个总转换的一小部分。随着回放容量的增加，n步可能不再是有益的，甚至是有害的。之所以会出现这种退化，是因为在确定回放率(这是实践中最常用的设置)时，最新策略年龄会随着回放容量的增加而增加。如第3.2节所示，每个因素的确切设置都控制着由最旧策略的增加所引起的退化的幅度以及由回放容量的增加而引起的改进的幅度。此外，n步回报的未经校正的性质可能会损害高异策性的机制下的性能。

　　因此，为了检验假设的极限，即n步回报在大容量机制下具有高水平的异策性的情况下有用，我们转向逻辑上的极端——离线RL(Agarwal et al., 2019)。在离线RL中，仅使用从另一个智能体收集的数据来训练学习者。保留原始智能体的所有数据，这与在线RL中的典型情况不同，在线RL中的典型情况是从回放缓存中逐出较旧的经验。这也代表了异策性的最坏情况，因为学习者无法与环境互动以更正其估计。我们使用Agarwal et al. (2019)的设置，对于之前实验中相同游戏子集中的每个游戏，DQN智能体收集一个200M帧的数据集，用于训练另一个智能体。我们用n步回报训练DQN的两个变体，并将n的每个设置与用于生成数据的在线DQN智能体进行比较。结果如图8所示。

　　即使在这项艰巨的任务中，使用n > 1也会持续提高两种智能体的性能。当改变n时，曲线的形状取决于所使用的特定智能体，但是设置n = 3 (这是所有先前实验中使用的值)效果很好。这些结果进一步证实了以下假设：增加回放容量时，n步是有益的。

5. Why is n-step the enabling factor?

　　在上一节中，我们从经验上证明了n步回报调节DQN是否可以利用更大的回放容量。在本节中，我们尝试揭示将这两个看似无关的组件链接在一起的机制。在我们评估的假设中，我们发现这在n步和回放容量之间的联系中起着部分作用。

5.1. Deadening the deadly triad

　　Q值的函数近似，目标中的自举以及异策学习已被确定为deadly triad (Sutton＆Barto, 2018；van Hasselt et al., 2018)的这些属性组合在一起时会对学习产生负面影响，甚至引起发散。van Hasselt et al. (2018)认为n步回报之所以有效，是因为它们使自举的幅度更小，从而减少了发散的可能性。回想一下，n步目标为，其中γ ∈ [0, 1)是折扣因子，γⁿ是收缩因子。收缩因子越小，自举Q(s_t+n, a)对目标的影响就越小。

　　如果在保持回放率不变的情况下增加回放容量，则缓存中的转换来自较旧的策略，这可能会增加数据的异策性，并且根据deadly triad的说法，这会使训练不稳定。因此，可以假设需要由n步提供的假定的稳定性来抵消较大的回放容量所产生的异策性增加。

　　我们通过对DQN应用具有与n步更新()相同的收缩因子的标准的1步更新来测试该假设(这等效于简单地减小折扣因子)。如果收缩因素是关键因素，那么使用DQN和修改后的更新应该可以通过增加回放容量来进行改进。但是，从经验上我们发现，在1步更新中使用较小的收缩因子时，增加回放容量并没有改进。此外，即使最旧的策略是固定的，应该控制关闭策略，DQN也不会随着容量的增加而提高(参见图7)。这些结果表明，n步的稳定性提升可以抵消异策性不稳定的假设，但并不能解释n步在利用更大的回放容量中的重要性。

5.2. Variance reduction

　　人们可以将n步回报视为估计蒙特卡罗(MC)目标和单步TD目标r_t + γ · max_aQ(s_t+1, a)之间的插值。它试图在MC目标的低偏差但高方差与单步TD目标的低方差但高偏差之间取得平衡。MC目标的方差来自奖励和环境动态的随机性，而单步TD目标的偏差来自于使用不完善的自举法来估计未来回报。

　　我们怀疑通过增加回放容量可以部分缓解n步回报相对于单步TD目标的额外方差。我们强调，我们在讨论目标的方差，而不是学习者的梯度方差。具体而言，目标函数将||Q(s_t, a_t) - E[G_t]||²最小化，其中G_t是目标，并且增加数据量可提供对E[G_t]的更好估计。这个简短的分析提供了一个可检验的假设：在回报方差较小的环境中，应减少增加回放容量的收益。通过关闭粘性动作，可以减少Atari域中回报的方差。粘性动作(Machado et al., 2018)使先前采取的动作以一定的固定概率重复出现，这可以看作是增加了转换动态的随机性，进而增加了回报的方差。

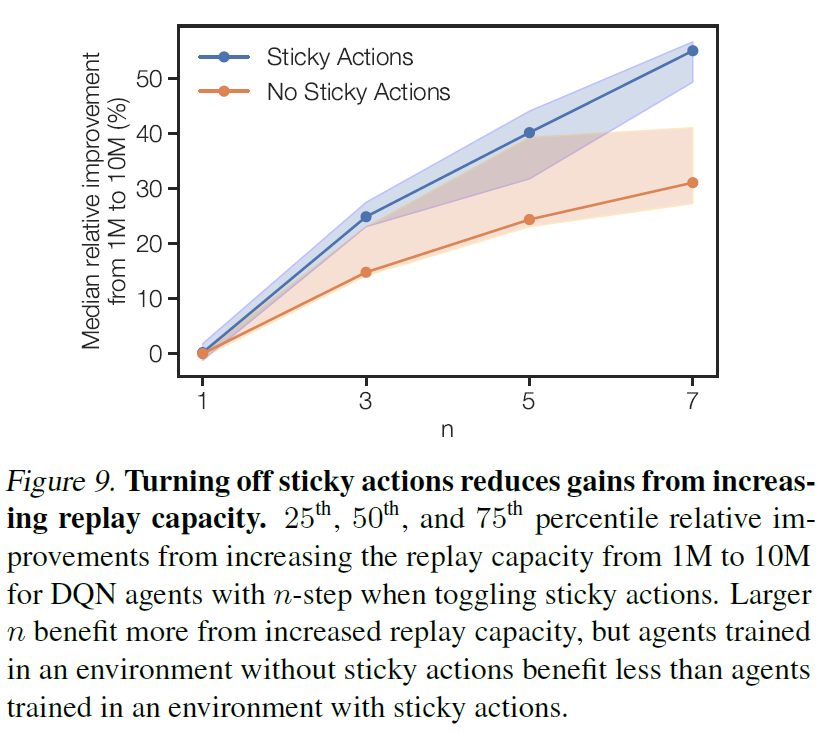
　　我们通过在带有和不带有粘性动作的ALE上运行DQN的1、3、5和7步版本来测试该假设，并将结果报告在图9中。如该假设所预测，没有粘性动作始终小于存在粘性动作的相对改进。此外，粘性动作和无粘性动作之间的改进差异随n的增加而增加，这是由假设预测的，因为方差也随n的增加而增加。但是，即使在消除随机性的情况下，使用n步回报仍然显示出容量增加的改进，这表明尽管有一些证据可以证明此处提出的假设，但它只能在解释n步更新的有效性及其使用更大缓存的能力方面发挥部分作用。

6. Discussion

　　我们对基于价值的深度RL智能体中的回放如何影响性能进行了深入研究。我们的贡献摘要如下：

理清回放容量和最旧策略的影响，发现增加回放容量和缩短最旧策略年龄可以提高性能；
发现n步回报对于利用增加的回放容量是至关重要的；
在大规模回放容量机制中以n步回报为基准，并发现尽管存在大量异策数据，它仍然可以带来收益；
研究n步回报和经验回放之间的联系，发现增加回放容量可以帮助减小n步目标的方差，这在一定程度上解释了性能的提高。

　　退后一步，这可以被解释为对第2.1节中描述的深度RL智能体的两个主要方面(即学习算法和数据生成机制)如何相互影响的研究。这两个方面有着千丝万缕的联系。训练算法所依据的数据显然会影响学习到的知识，相应地，学习到的知识也会影响智能体与环境的交互方式，从而生成哪些数据。我们重点介绍了数据生成分布的几个基本属性：(a) 同策程度(数据生成分布与当前正在评估的策略有多接近？)；(b) 状态-空间范围；(c) 转换之间的相关性；(d) 分布支持的基数。
　　实际上，这些方面可能很难独立控制，我们可以进行的典型算法调整会同时影响其中的几个方面。此类调整的两个示例是本文研究的回放容量和回放率。我们强调，根据智能体的精确结构，智能体的这些实际上可控的方面也可能对数据分发本身产生不同的影响。例如，在R2D2 (Kapturowski et al., 2019)之类的分布智能体中，通过增加执行者数量来降低回放率将导致上述(a)和(c)的变化，而在单个执行者的智能体(例如DQN)，通过更改每个梯度步骤的环境步骤数来更改回放率也将更改(b)。

　　这些问题凸显了在实际算法调整水平上数据生成机制的这些不同属性之间存在的纠缠，并激发了对如何解开这些属性的进一步研究。对于获得可以随数据的可用性而轻松扩展的智能体而言，这一研究方向特别重要。从更广泛的意义上讲，这项工作提出了许多问题，包括回放和其他智能体程序组件的交互作用，深度RL中n步回报的重要性以及异策学习，我们希望这对于未来的工作很有意义。

APPENDICES: Revisiting Fundamentals of Experience Replay

A. Experimental Details

A.1. Dopamine Rainbow Agent

　　本文中的实证研究基于Dopamine Rainbow智能体(Castro et al., 2018)。这是原始智能体的开源实现(Hessel et al., 2018)，但是做出了一些简化的设计选择。原始智能体通过使用(a) 分布学习目标，(b) 多步回报，(c) Adam优化器，(d) 优先回放，(e) 双重Q学习，(f) 对偶结构，以及(g) 带噪的探索网络。Dopamine Rainbow智能体仅使用这些调整的前四个，在Hessel et al. (2018)的原始分析中被确定为该智能体最重要的方面。

A.2. Atari 2600 Games Used

　　14个游戏子集用于网格，用于度量变化的回放容量和最旧策略的影响。所有其他实验均使用20个游戏子集，其中包括用于网格的14个游戏和另外6个游戏。

14 game subset: AIR RAID, ASTERIX, BREAKOUT, FREEWAY, GRAVITAR, JAMES BOND, MONTEZUMA’S REVENGE, MS. PACMAN, PRIVATE EYE, Q*BERT, SEAQUEST, SPACE INVADERS, VENTURE, ZAXXON

20 game subset: 上面的14个游戏以及下列6个游戏：ASTEROIDS, BOWLING, DEMON ATTACK, PONG, Wizard OF WOR, YARS'REVENGE

B. Additive and Ablative Studies

B.1. DQN Additions

　　我们在图10中提供了每个补充DQN智能体性能的游戏级别粒度。

B.2. Rainbow Ablations

　　我们提供了图11中每种消融的Rainbow智能体的性能的游戏级别粒度。

C. Error Analysis for Rainbow Grid

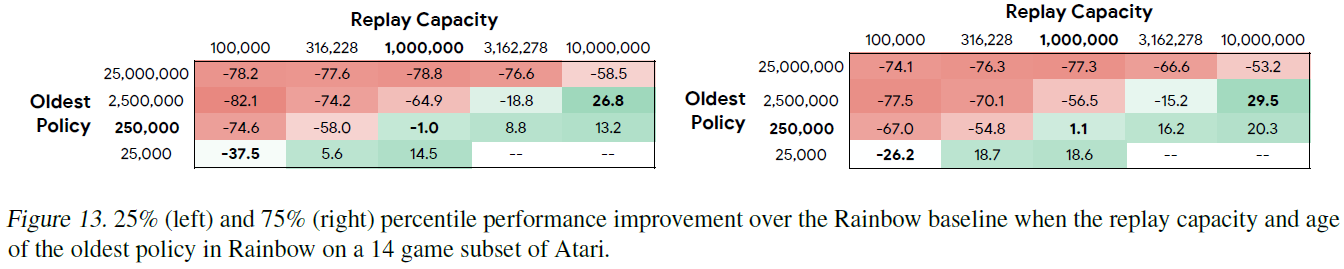
　　通过为回放容量和最旧策略的每种组合提供25％和75％的改进，我们为图2中的每个元素提供了误差分析。这些结果在图13中给出。

D. Replay Buffer Size

　　我们提供了具有不同缓存大小的Rainbow性能的游戏级别粒度，如图14所示。