Prefrontal cortex as a meta-reinforcement learning system

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

 Nature Neuroscience, 2018

 

Abstract

　　在过去的20年中，基于奖励的学习的神经科学研究已经集中在经典模型上，在该模型中，神经递质多巴胺通过调节神经元之间突触连接的强度，在情况，动作和奖励之间建立联系。然而，越来越多的最新发现使该标准模型处于压力之下。现在，我们利用AI的最新进展来介绍基于奖励的学习的新理论。在这里，多巴胺系统训练大脑的另一部分，即前额叶皮层，作为其自己的独立式学习系统进行操作。
　　这种新的观点容纳这样一种发现：既激励标准模型，又可以优雅地处理更广泛的观察结果。这为将来的研究提供了新的基础。

 

　　最近，在理解奖励驱动学习所涉及的机制方面取得了令人振奋的进步。通过从强化学习¹（RL）领域引入思想，部分地实现了这一进步。最重要的是，这种输入导致了基于RL的多巴胺能功能理论。在这里，多巴胺（DA）的释放被解释为传达了奖励预测误差（RPE）信号²，这是在时序差分RL算法中集中体现的惊喜指数。根据该理论，RPE驱动纹状体中的突触可塑性，将经验丰富的动作-奖励联系转化为优化的行为策略³。在过去的二十年中，这一提议的证据不断增多，并将其确立为奖励驱动学习的标准模型。
　　但是，即使此标准模型已经固化，也积累了一些有问题的观察结果。对前额叶皮层（PFC）的研究产生了一个难题。越来越多的证据表明，PFC实现了基于奖励的学习机制，执行的计算与基于DA的RL的计算极为相似。早已确定，PFC的扇区代表动作，对象和状态的期望价值^4-6。最近，已经出现了PFC还对最近的动作与奖励历史进行编码^5,7-10。编码的变量集以及有关PFC中神经激活的时间分布的观察结果得出以下结论：“PFC神经元动态地[编码]从奖励与选择历史到对象价值，以及从对象价值到对象选择的转换”⁷。简而言之，PFC中的神经活动似乎反映了一组操作，这些操作一起构成了独立的RL算法。

　　将PFC放置在DA旁边，我们获得了一张包含两个完整RL系统的图片，一个使用基于活动的表征，另一个使用突触学习。这些系统之间是什么关系？如果两者都支持RL，那么它们的函数是否仅仅是多余的？一种建议是，DA和PFC支持不同形式的学习，其中DA基于直接刺激-响应关联实现了无模型RL，而PFC执行了有模型RL，从而利用了任务结构的内部表征^11,12。但是，对于这种双系统视图，一个明显的问题是重复观察到DA预测误差信号是由任务结构通知的，反映了很难与最初构架的标准理论相吻合的“推断”^12,13和“有模型”^14,15的价值估计。

　　在当前的工作中，我们为基于奖励的学习的基础计算提供了一个新的视角，该视角适应了由上述现有理论启发的发现，但也解决了许多普遍的难题。在更广泛的层面上，该理论为先前被认为无关的各种发现提出了一个连贯的解释。我们从三个关键前提开始：

　　System architecture. 与先前的工作^16-18一致，我们将PFC以及与其连接的基底神经节和丘脑核概念化，形成了RNN。该网络的输入包括感知数据，该数据包含或伴随着有关已执行动作和所获得奖励的信息¹⁹。在输出端，网络触发动作并发出状态价值的估计（图1a,b）。

　　Learning. 正如过去研究^20-22中所建议的那样，我们假设前额叶网络（包括纹状体成分）中的突触权重是通过无模型RL程序进行调整的，其中DA传递RPE信号。通过这个角色，基于DA的RL程序可以改变循环前额叶网络的激活动态。

　　Task environment. 根据过去的提议^23–25，我们假设RL不是在单个任务上发生，而是在动态环境中构成一系列相互关联的任务。因此，需要学习系统进行持续的推断和行为调整。

　　如前所述，这些前提都牢固地立足于现有研究。当前工作的新贡献是确定在同时满足三个前提时产生的新效果。正如我们将要展示的，当这些条件同时发生时，它们足以产生一种“元学习”²⁶的形式，其中一种学习算法会产生第二种更有效的学习算法。具体来说，通过调整前额叶网络中的连接权重，基于DA的RL创建了第二个RL算法，该算法完全在前额叶网络的激活动态中实现。这种新的学习算法独立于原始算法，并且在适合任务环境的方式上有所不同。至关重要的是，新兴算法是成熟的RL程序：它可以解决探索与开发之间的折衷问题^27,28，保持了对价值函数¹的表征，并逐步调整了动作策略。考虑到这一点，并认识到一些先驱研究^29-32，我们将总体效果称为“元强化学习”。

　　为了演示，我们利用图1a中所示的简单模型，即RNN（图1b），该模型的权重使用无模型RL算法进行训练，利用了深度学习研究的最新进展（请参见方法和补充图1）。我们在简单的“双臂赌博机” RL任务中考虑了该模型的性能。在每次试验中，系统都会输出一个动作：左或右。每个臂都有产生奖励的可能性，但是这些概率随每个训练回合而变化，从而提出了一个新的赌博机问题。在对一系列问题进行了训练之后，固定了循环网络中的权重，并对系统进行了进一步的问题测试。该网络探索了双臂，逐渐地转向奖励较多的臂，其学习效率可与标准的机器学习算法相媲美（图1c,d）。

　　由于网络中的权重在测试时是固定的，因此系统的学习能力不能归因于用于调整权重的RL算法。相反，学习反映了循环网络的激活动态。作为训练的结果，这些动态实现了自己的RL算法，随着时间的推移集成了奖励信息，探索并改进动作策略（图1e,f和补充图2）。该学习到的RL算法不仅可以独立于最初用于设置网络权重的算法运作。它与原始算法的不同之处还在于，它特别适合于训练系统的任务分布。在图1d中给出了这一点的说明，该图显示了在对赌博机问题的结构化版本进行训练后同一系统的性能，其中在各个回合中的臂参数是反相关的。在这里，循环网络收敛于利用问题结构的RL算法，与非结构化任务相比，可以更快地识别出较优臂。

　　在以抽象计算术语介绍了元RL之后，我们现在返回到其神经生物学解释。首先将前额叶神经网络（包括其皮层下成分）视为RNN。与标准模型一样，DA广播RPE信号，从而驱动前额叶网络中的突触学习。此学习的主要作用是通过调整前额叶网络的循环连接来塑造其动态。通过元RL，这些动态实现了第二种RL算法，该算法与原始DA驱动的算法不同，并采用了适合任务环境的形式。在此基础上，DA驱动的RL在扩展的一系列任务中扮演着角色。快速的任务内学习主要是由前额叶网络动态中固有的新兴RL算法导致的。

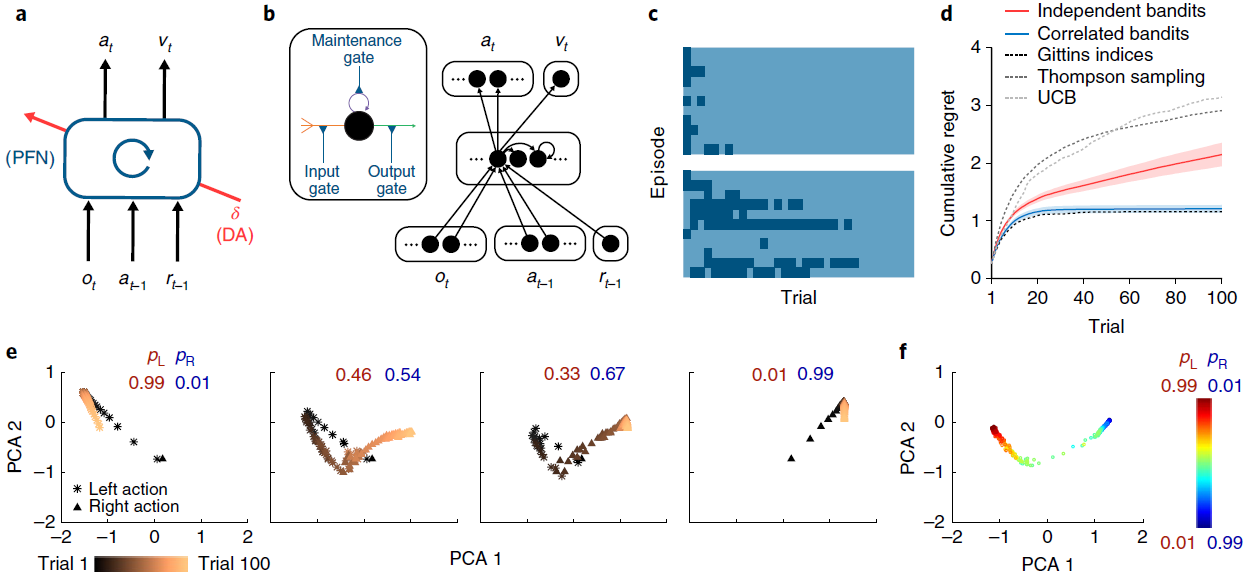
图1 |  元RL结构可跨回合学习，以在回合内有效学习。a，智能体架构。前额叶网络（PFN），包括直接与PFC连接的基底神经节和丘脑的部分，被建模为RNN，其突触权重通过DA驱动的RL算法进行调整；o是感知输入，a是动作，r是奖励，v是状态价值，t是时间步骤，δ是RPE。中央框表示一组全连接的LSTM单元。b，在我们的仿真中实现的神经网络的详细示意图。编码当前观察值，先前动作和奖励的输入单元将所有数据与隐含单元连接在一起，而隐含单元本身就是全连接的LSTM单元。这些单元依次通过softmax层（请参见方法）对动作进行编码，并使用一个线性单位对估计的状态价值进行编码，从而将所有数据连接在一起。插图：单个LSTM单位（请参见方法）。输入（橙色）是其他单位输出的加权和，加上LSTM单位本身的活动（紫色）。输出（绿色）使这些求和的输入经过sigmoid非线性。所有三个量都被乘以门（蓝色）。在方法中提供了包括相关方程在内的全部详细信息。c，对于具有Bernoulli（第1臂，第2臂）奖励参数0.25, 0.75（顶部）和0.6, 0.4（底部）的赌博机问题的逐次试验模型行为。这两种颜色分别指示左动作和右动作。网络从探索向开发转换，使这一转换在更困难的问题上更加缓慢。d，在具有独立同分布的臂参数的赌博机上训练的元RL网络的性能，并在0.25, 0.75（红色）上进行了测试，以累积遗憾的方式衡量，定义为选择次优（较低的奖励）臂时遭受的累积损失（以期望奖励计）。绘制了几种标准机器学习赌博机算法的性能以进行比较。蓝色表示经过对相关赌博机的训练（相同参数总和为1）后在同一个问题上的性能。阴影表示300次评估回合中的95％置信区间。e，在训练来自同一分布的问题后，在对相关赌博机进行测试时，在个别试验中RNN激活模式的演变。p_L表示动作“左”的奖励概率；p_R表示采取动作“右”的奖励概率。f，从相关的赌博机任务中的步骤100开始，在一系列奖励参数上的RNN活动模式。补充图2给出了进一步的分析。通过1个训练有素的网络对300个评估回合进行了分析，每个回合包括100个试验。

 

Results

　　尽管它很简单，但元RL框架可以解释令人惊讶的神经科学发现，包括许多对DA的标准RPE模型带来困难的结果。为了调查框架的影响，我们进行了六个模拟实验，每个模拟实验着重于选择用来说明该理论核心方面的一组实验结果。在整个仿真过程中，我们继续应用图1a中的简单计算架构。这种方法显然抽象出许多神经解剖学和生理学细节（参见补充图3）。但是，它可以让我们在易于确定其计算来源的环境中演示关键效果。本着同样的精神，我们的模拟不仅仅关注与参数相关的数据拟合，而仅关注鲁棒的定性效果。

 

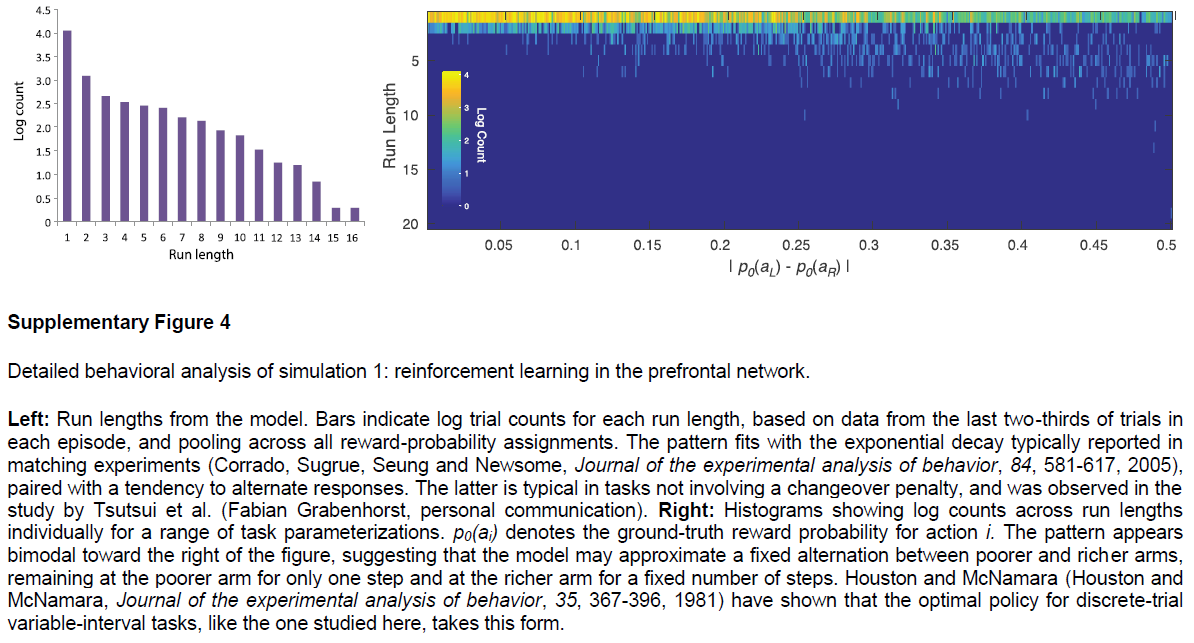
Simulation 1: RL in the prefrontal network. 我们从PFC编码被整合到逐步形成的选择价值表征中的最近的动作与奖励这个发现开始。为了证明元RL如何解释这一发现，我们模拟了Tsutsui et al.⁷以及Lau and Glimcher³³的结果。两项研究都采用了一项任务，即猴子在两个视觉扫视目标之间进行选择，每个目标都能以间歇性变化的概率获得汁液奖励。在给定奖励计划的情况下，可以通过按照目标的产出对每个目标进行采样来估计最优策略³³，而猴子则表现出这种“概率匹配”（图2a）。背外侧PFC⁷的记录显示了编码先前试验中选择的对象的活动，获得的奖励，目标的更新价值以及每个即时动作（图2b），支持了PFC神经元反映逐项试验构造的结论，并根据最近的经验更新选择价值¹⁰。

　　我们通过在同一任务上训练元RL模型来模拟这些结果（请参见方法）。网络将其行为调整为适合每个任务实例，显示与并行实验结果非常相似的概率匹配（图2d）。细粒度分析得出的模式类似于在猴子行为中观察到的模式（图2c,f和补充图4）。请注意，该网络的权重在测试时是固定的，这意味着该网络的行为只能由前额叶RNN活动的动态导致。与此相一致，我们在前额叶网络中发现了对Tsutsui et al.⁷报告的每个变量进行编码的单元（图2e）。
　　这些结果提供了元RL活动的另一种基本说明，DA驱动的训练产生了独立的基于前额叶的学习算法。在这种情况下，元RL解释了实验数据中观察到的行为和PFC活动，但也解释了通过DA驱动的学习如何同时出现这两种行为。

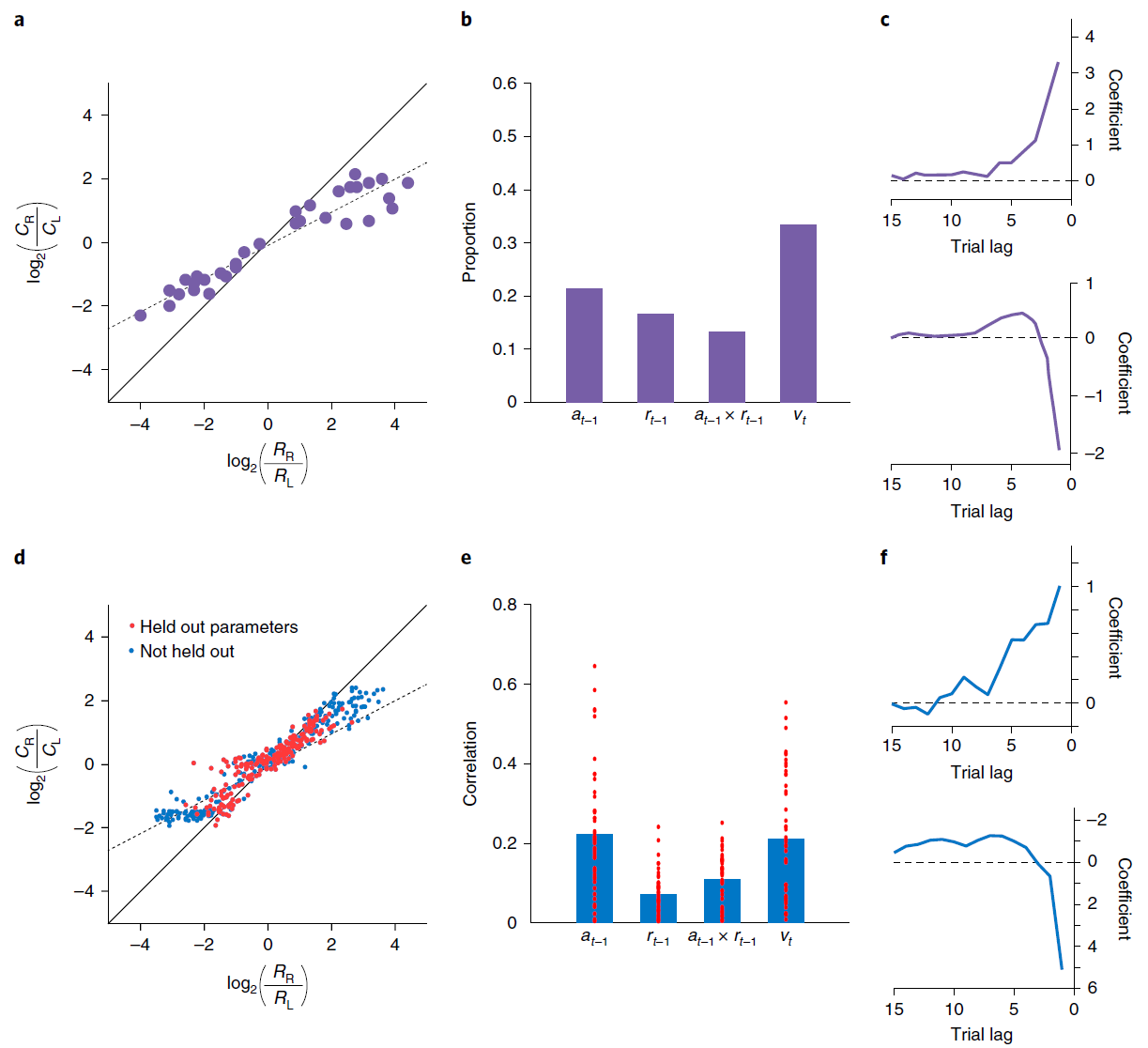
图2 | 模拟循环网络代码中的各个单元，用于记录动作和奖励历史记录。a，来自Lau and Glimcher的概率匹配行为³³。C_i表示选择动作 i 的试验次数；R_i表示由动作 i 产生的奖励事件的数量。b，来自Tsutsui et al.⁷的PFC神经元编码的比例，在试验的初始固定时期，先前动作，先前奖励，这两个因素的相互作用以及当前选择价值。c，滞后回归系数表明从Lau and Glimcher³³中选择最近奖励的影响（顶部）和动作（底部）。d，模型匹配行为。红点表示泛化性能（请参见方法）。e，与b中相同的因素的偏相关系数（绝对值，Pearson的r），但在试验初次固定时跨模型中的各个单元。条形表示平均值。即时动作（未显示）的编码在单位之间也很普遍，并且通常比其他变量要强。f，回归权重与c中的权重相对应，但基于模型行为。c和f之间的系数尺度差异是由于回归程序中的微小差异所致，特别是使用了奖励历史 vs. 连续值（范围从0.35到0.6）。为了进行比较，Ttsutsui et al.⁷报告了过去奖励的影响的回归结果，该结果表明时间分布相似，但在滞后1达到峰值，系数为1.25。面板a-c经Tsutsui et al.⁷以及Lau and Glimcher³³的许可改编。

 

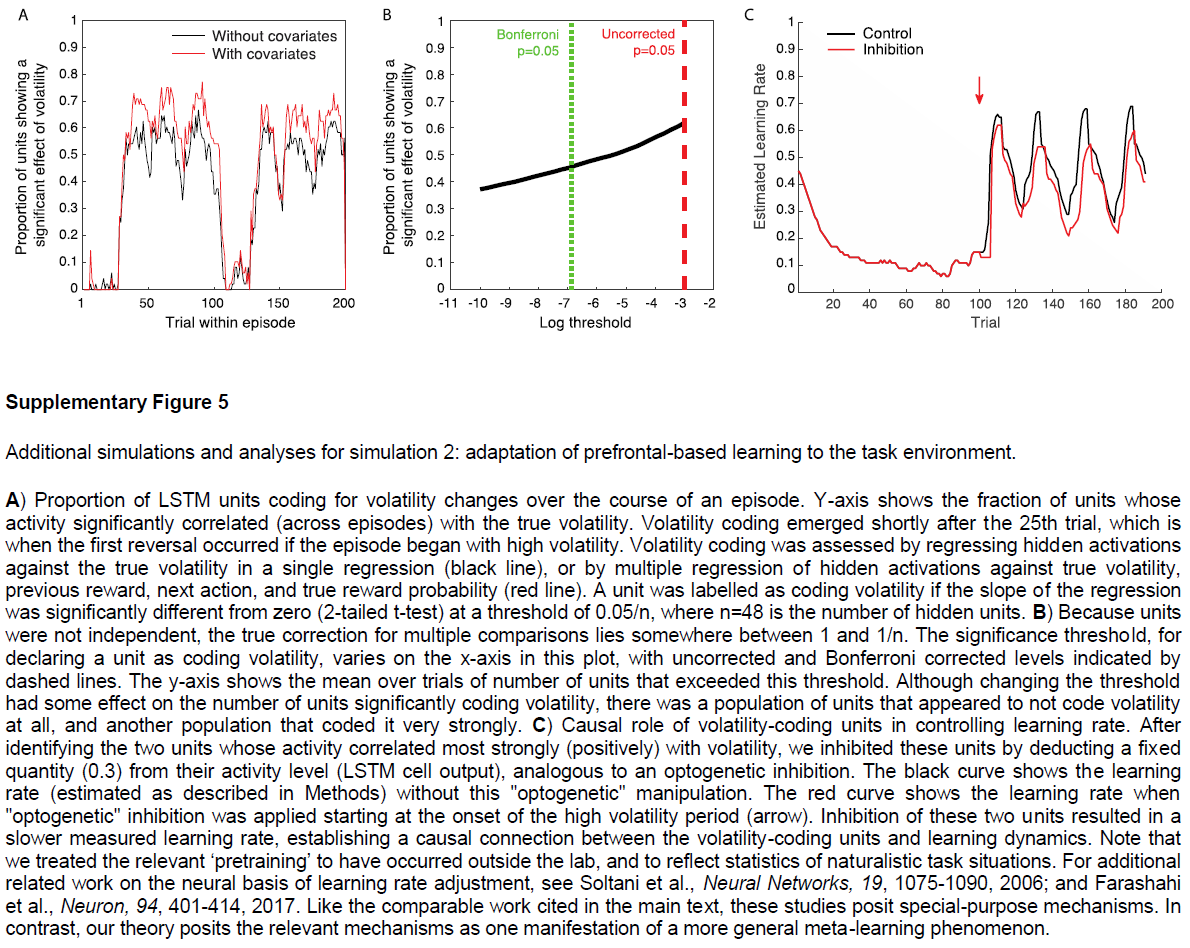
Simulation 2: adaptation of prefrontal-based learning to the task environment. 元RL的一个关键方面是，在前额叶网络中出现的学习算法可能不同于创建它的基于DA的算法。我们在这里说明该原理，重点放在单个参数的差异上：学习率。为此，我们模拟了Behrens et al.[34]的实验结果。 这涉及到双臂赌博机任务，在回报概率保持稳定的“稳定”时期和波动的“不稳定”时期之间交替。Behrens et al.[34]发现，与贝叶斯模型确定的最优策略相一致（根据任务波动的动态估计来调整其学习率），人类参与者在不稳定时期所采用的学习率要比稳定时期快（将3a,c进行对比）。神经影像数据确定了PFC内的一个区域（特别是背扣带回皮层），该区域的活动跟踪了贝叶斯模型的波动率估计。

　　图3b,d总结了在相同任务下具有固定权重的模型的行为。 该模型以前在一系列具有变化的波动回合中进行过训练（请参见“方法和补充图5”），以模仿人类参与者执行任务时所经历的不同波动的先验经验。像人类学习者一样，网络可以动态地使其学习率适应不断变化的波动性。而且，正如用fMRI观察到的PFC活动一样，LSTM网络中的许多单位（37±1％）明确跟踪了波动性。
　　至关重要的是，图3d所示的学习率比管理基于DA的RL算法的学习率大几个数量级，后者在训练过程中调整了前额叶网络的权重（设置为0.00005）。因此，结果提供了具体的说明，说明了从元RL产生的学习算法可能与最初产生它的算法不同。结果还使我们能够强调该原理的重要推论，即元RL产生了实际上适合于任务环境的前额叶学习算法。在当前情况下，这种适应以学习率响应任务波动的方式体现出来。先前的研究提出了特殊目的机制来解释学习率的动态变化^29,35。元RL将这些变化解释为一种新兴效果，是由一系列非常普遍的条件引起的。而且，动态学习率只是专业化的一种可能形式。当元RL在具有不同结构的环境中出现时，将出现不同定性的学习规则，这一点将在后续的模拟中得到说明。

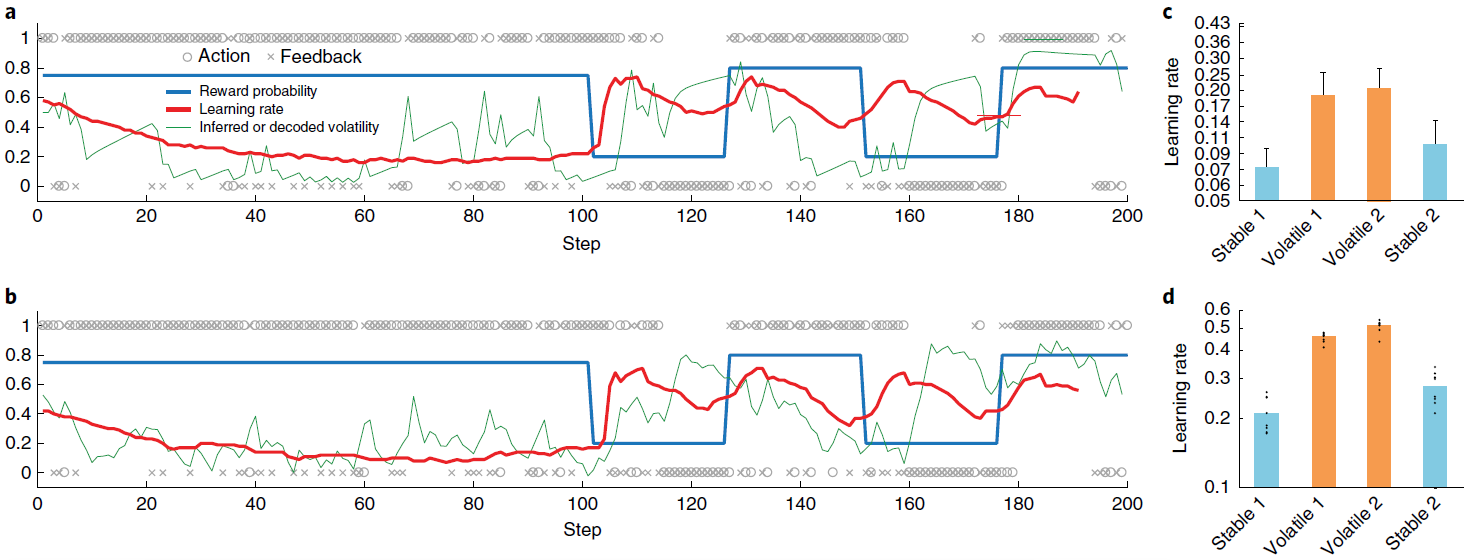
图3 | 学习型RL算法可根据环境的变化动态调整其学习率。a，Behrens et al.³⁴在其不稳定赌博机任务上提出的贝叶斯模型的样本行为。蓝色是动作1的真实奖励概率（动作1和2的概率总和为1）；o表示动作（上面为动作1，下面为动作2）；x表示结果（上面为奖励，下面为无奖励）。绿色是预计波动率；红色是学习率。b，元RL模型的相应数量，如方法中所述对不稳定性进行解码。c，从Behrens et al.³⁴重新绘制的人类行为摘要，显示了测试样本在s.e.m的情况下的平均学习率。d，相应的元RL行为表现出相似的模式，在不稳定任务块中具有较高的学习率。点代表来自采用不同随机种子的单独训练（n = 8）的数据。面板a和c经Behrens et al.³⁴许可改编。

 

Simulation 3: reward prediction errors reflecting inferred value. 如前所述，标准模型的一个明显挑战是DA的RPE信号反映了任务结构的知识。一个例子就是Bromberg-Martin et al.¹²报告的“推断价值”效应。在执行任务的每个试验中，视觉目标都出现在显示器的左侧或右侧，并且猴子被期望扫向目标。在实验的任何时候，左目标或右目标都会产生汁液奖励，而另一边则不会，并且这些角色分配在整个测试过程中会间歇性地反转。关键观察到的是反转后DA信号的变化：在猴子对一个目标的奖励发生变化之后，DA立即对另一个目标的出现做出了显著变化，反映出该目标的价值也发生了变化（图4a）。

　　这种推断价值效应以及其他相关发现引出了模型，其中PFC或海马体对抽象的隐状态表示进行编码^19,36-38，然后可以将其送入生成RPE¹³的计算中。事实证明，相关的机制自然是由元RL引起的。为了证明这一点，我们在Bromberg-Martin et al.的任务¹²中训练了元RL模型。在测试中，我们观察到RPE信号复制了DA显示的模式。特别是，该模型清楚地再现了关键推断价值效应（图4b）。
　　此结果的解释很简单。在我们的结构中，RPE的奖励预测组件来自前额叶网络的状态价值输出，该数据与表明DA信号受PFC的预测影响的数据一致¹³。由于基于DA的训练使前额叶网络对有关任务动态的信息进行编码（图4c），因此该信息也体现在RPE的奖励预测组件中。

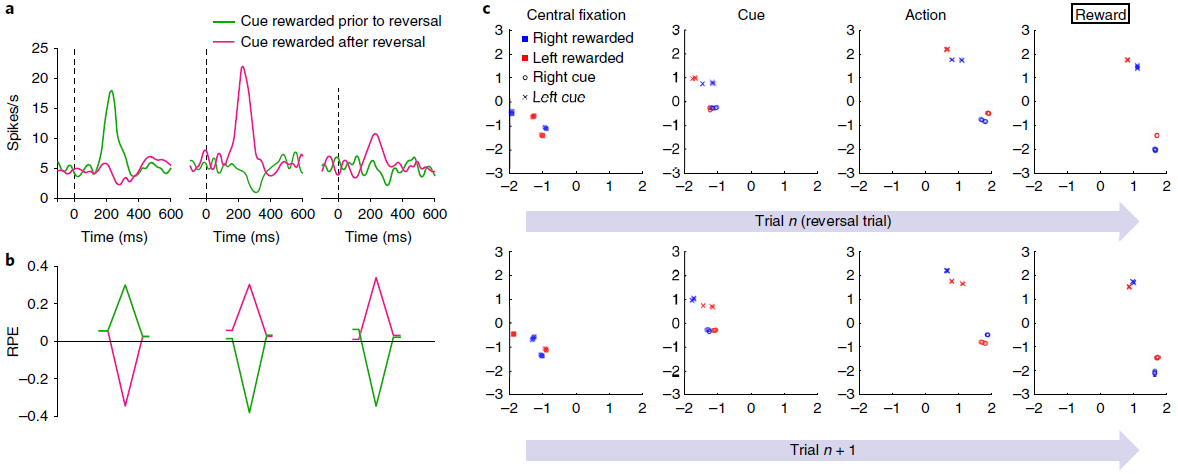
图4 | 模拟智能体的奖励预测误差与猴子中观察到的相似，反映的是推断价值，而不仅是经验价值。a，结果经Bromberg-Martin et al.¹²许可改编。多巴胺能活动响应于反转之前的信号（左）以及具有经验价值（中间）和推断价值（右）变化的信号。曲线代表了两只猴子的平均神经元响应（每条曲线n = 42-63）。b，来自模型的相应RPE信号。每个数据系列的起点和终点对应于初始注视和扫视步骤。峰谷对应于刺激表现。虽然经验数据中的RPE响应对于推断价值较小，但此处未显示，但Bromberg-Martin et al.¹²的其他经验结果显示了更多相似的模式。尤其是，在相同任务中不同动物的侧面habenula记录在条件下产生的RPE信号（和行为反应时间）相似得多。c，模拟3任务中各个步骤的RNN活动（LSTM输出）的前两个主要成分，由1个训练有素的网络副本执行的1200个评估回合进行了分析。其他副本产生了非常相似的结果。最上面的一行着眼于反转试验，在该试验中，最终的奖励反馈（最右边的面板）表示奖励目标已经相对于先前的试验进行了反转。第二行重点关注第一行检查的反转试验之后的试验。活动模式根据任务的当前隐状态（即当前提示哪种信号）进行聚类，随后在每个试验中也根据选择的动作进行聚类。如最左边的面板（“中央注视”）所示，在每次试用开始时，网络的激活状态代表任务的隐状态，并且在进行反转试验后突然恢复。

 

Simulation 4: ‘model-based’ behavior—the two-step task. 观察到结构敏感的DA信号的另一个重要设置是在旨在探测有模型的控制任务中。在这一类别中，研究最深入的任务也许是Daw et al.[15]引入的“两步”模型。在我们将考虑的版本中（图5a），每个试验都始于两个动作之间的决定。每个触发概率转换到两个可感知区分的第二阶段状态之一；对于每个动作，都有一个“常见”（高概率）转换和一个“罕见”（低概率）转换。然后，每个第二阶段状态都会提供具有特定概率的奖励，该奖励会间歇性地反转（请参见方法）。

　　两步任务的有趣点在于它能够区分无模型学习和有模型学习。最重要的是异常反转后的行为。考虑在阶段1选定的触发罕见转换并随后得到奖励的动作。由动作-奖励关联驱动的无模型学习将增加在后续试验中重复相同的第一阶段动作的可能性。相反，有模型学习将考虑任务的转换结构，并增加选择相反动作的可能性（图5b）。人类¹⁵和啮齿动物³⁹都通常表现出有模型学习的行为证据（图5c,d）。
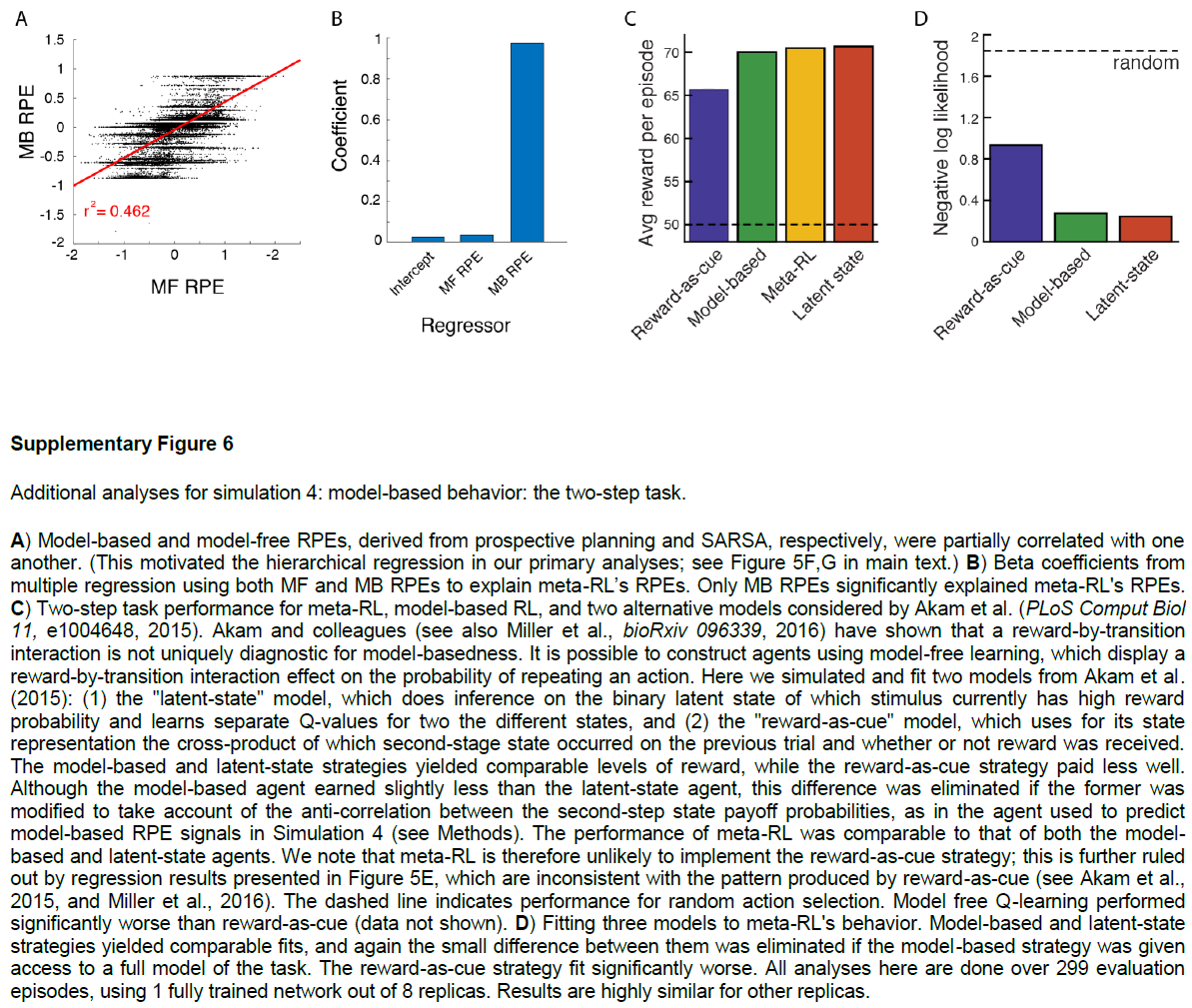
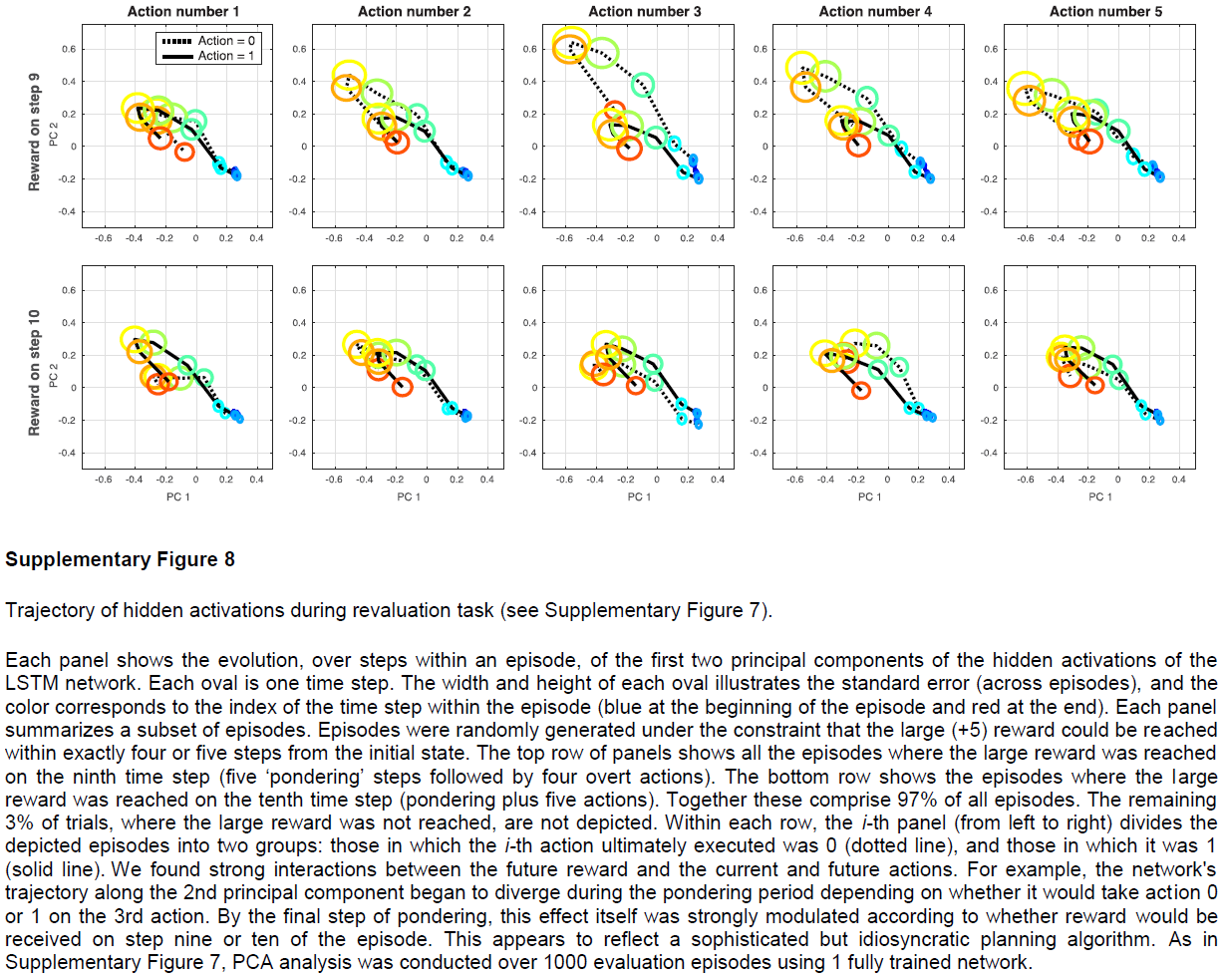
　　我们在两步任务上训练了我们的元RL模型（请参阅方法），发现在测试中其行为采取了与有模型控制相关的形式（图5c,e）。与以前的模拟一样，在冻结权重的情况下测试了网络。因此，观察到的行为是由循环前额叶网络的动态产生的。但是，重要的是要记住，网络是由无模型的DA驱动的RL算法训练的。在神经科学的背景下，这表明了一个有趣的可能性，即有模型RL的PFC实现实际上可能源于无模型的DA驱动的训练（进一步的分析，请参见图6-8）。
　　至关重要的是，两步任务是报告结构敏感的RPE信号的最早背景之一。Daw et al.¹⁵特别使用fMRI，观察了人类腹侧纹状体中的RPE（DA的主要目标），该RPE跟踪了有模型RL算法预测的RPE。在我们的元RL模型中也会产生相同的效果（图5f,g）。

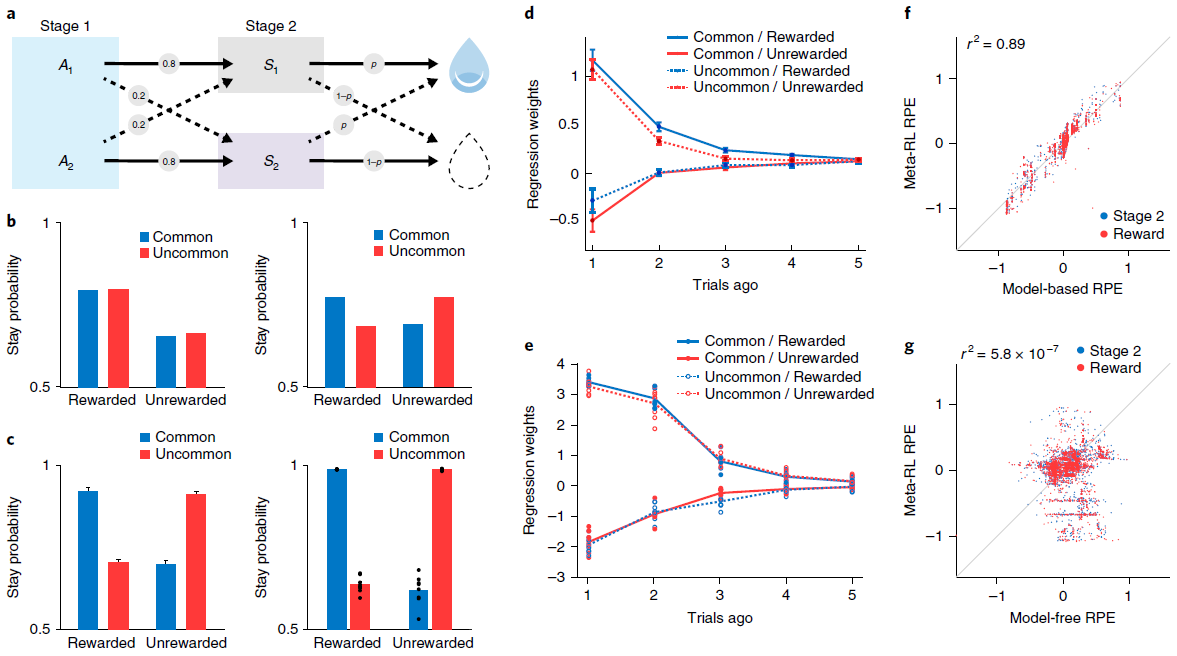
图5 | 学习到的RL算法可显示有模型的行为和RPE。a，两步任务的结构^15,39，描述了第一阶段动作A₁和A₂如何概率性地转换到第二阶段状态S₁和S₂。b，顶部，无模型（左）和有模型（右）学习的典型行为模式。c，左图，来自Miller et al.³⁹的数据，显示了基于典型模型的动物行为模式。曲线表示n = 6只大鼠的平均停留概率；误差条为s.e.m. 有关完整分布，请参见Miller et al.³⁹。右图，网络的相应行为。点表示来自使用不同的随机种子（n = 8）单独训练的数据。d，Miller et al.³⁹的更详细的分析显示，在多个试验滞后，转换类型和奖励对动物行为的影响。该图表示n = 21只大鼠的平均回归权重；误差线为s.e.m. 该模式排除了另一种无模型的机制（请参见补充图6）。e，对元RL行为的相应分析。点表示来自使用不同的随机种子（n = 8）单独训练的数据。f,g，在试验的不同阶段，模型RPE信号相对于有模型（f）和无模型（g）算法的预测的回归。由8个副本中的1个经过充分训练的网络对30个评估回合进行了分析，每个回合包括100个试验。面板c（左）和d经Miller et al.³⁹许可改编。

 

Simulation 5: learning to learn. 模拟3和4集中于涉及任务的两个版本之间交替的场景，随着时间的推移，每个版本可能会变得很熟悉。在这里，我们将元RL应用于一项任务，在该任务中不断出现新的刺激，需要在最充分的意义上进行学习。在这种情况下，我们证明元RL可以说明过去的经验会加速新学习的情况，这种效果通常称为“学会学习”。

　　在最初启发该术语的任务中，Harlow⁴⁰向猴子展示了两个不熟悉的对象，一个是包含食物奖励的井，另一个是空井。动物在对象之间自由选择，并且如果奖励存在的话可以获取该食物奖励。然后随机重置对象的左右位置，并开始新的试验。在重复六次此过程之后，用两个全新的对象进行替换，然后再次开始该过程。在每个试验阶段中，选择一个对象始终给予奖励，而另一个始终不给奖励。在训练的早期，猴子在每个块中收敛到正确对象上的速度很慢。但是经过大量的练习，猴子只经过一次试验就表现出了完美的性能，这反映了对任务规则的理解（图6b）。
　　为了评估元RL解释Harlow⁴⁰的结果的能力，我们将他的任务转换为要求在模拟计算机显示器上呈现的图像之间进行选择的任务（图6a和补充视频1）。否则，该任务保持不变，每六个试验后引入一对不熟悉的图像。为了使我们的模型能够处理高维像素输入，我们使用常规的图像处理网络对其进行了扩充（请参见方法）。结果系统生成的学习曲线与经验数据非常相似（图6c）。经过训练，该网络在一次试验中学习了如何在每个新区域中做出响应，从而复制了Harlow⁴⁰的“学会学习”效果。

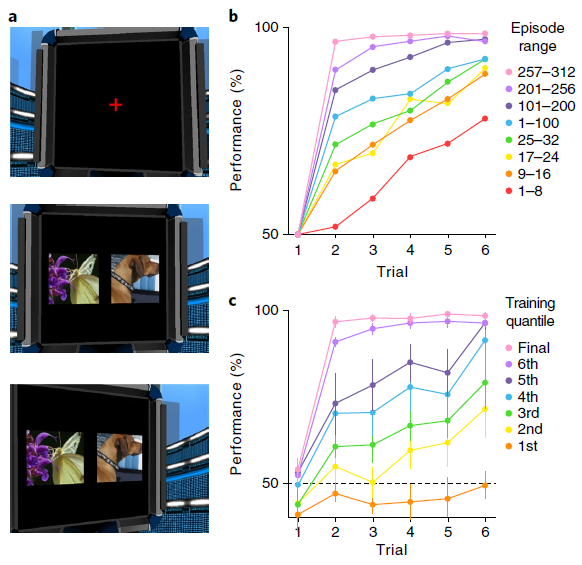
图6 |  元RL学习在视觉丰富的3D环境中学习抽象结构和新颖刺激。a，模拟5（全分辨率）的示例图像输入，显示了注视十字（上），初始刺激表现（中）和扫视结局（下）。b，在引入新对象之后以及在训练连接权重的多个点上，来自Harlow⁴⁰的每个步骤的精度数据。c，训练的七个连续阶段（请参阅方法）的模型性能，在达到最高性能（50个副本中）的所有网络（n = 14）中取平均值。误差条代表95％置信区间。

 

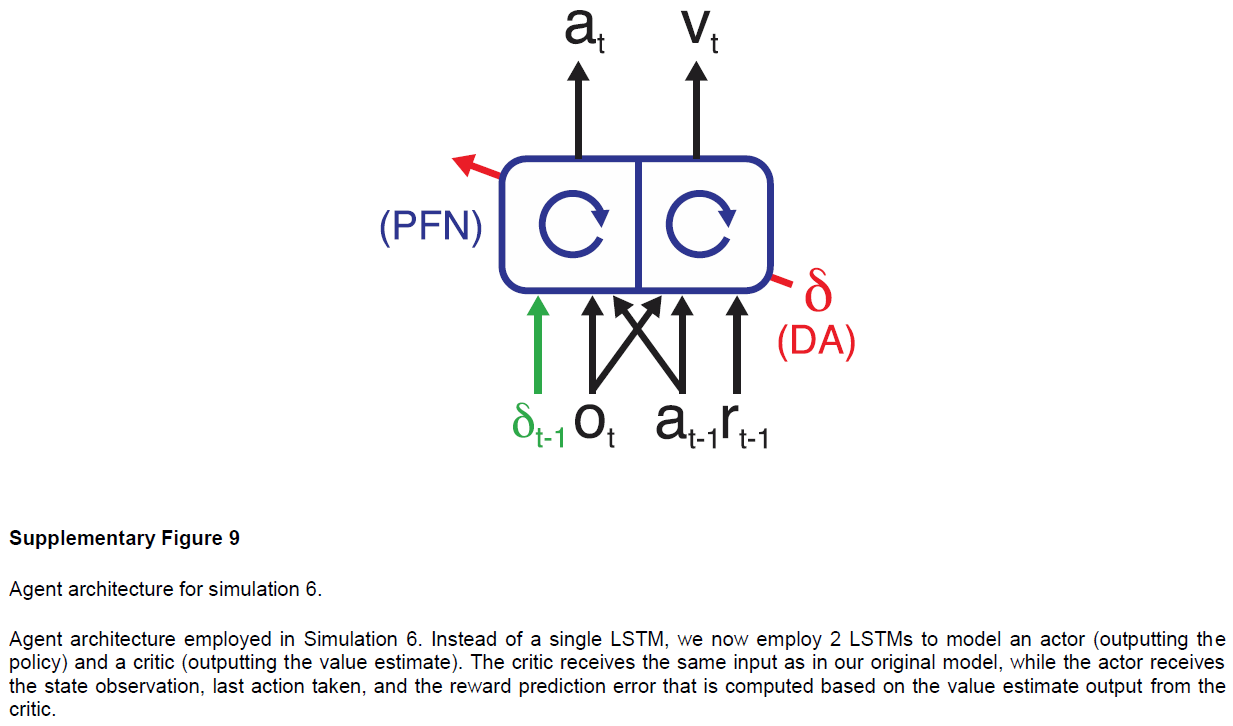
Simulation 6: the role of dopamine—effects of optogenetic manipulation. 元RL框架要求前额叶网络的输入包含有关最近奖励的信息。我们的实现通过输入标量信号来满足此要求，该标量信号明确表示在先前时间步骤上收到的奖励量（图1a）。但是，任何与奖励密切相关的信号就已足够。因此，诸如汁液的味道之类的感觉信号可能起必要的作用。另一个特别有趣的可能性是，有关奖励的信息可能由DA本身传达。在这种情况下，DA将扮演两个不同的角色。首先，与标准模型一样，DA将调节前额叶网络中的突触可塑性。其次，相同的DA信号将通过送入有关近期奖励的信息来支持前额叶网络中基于活动的RL计算⁴¹。我们修改了原始网络以提供RPE（代替奖励）作为该网络的输入（请参见方法和补充图9），发现它在模拟1–5的任务上产生了类似的行为。

　　元RL的这种变化为使用光遗传学技术阻断或诱导多巴胺能RPE信号的近期实验发现提供了新的解释^42,43。为了说明这一点，我们考虑了Stopper et al.⁴⁴进行的一项实验，该实验涉及具有间歇转换收益概率的双臂赌博机任务（请参见方法）。在从一个杆提供食物奖励期间阻止DA活动导致对该杆的偏好降低。相反，当一个杆无法产生食物时，人为地刺激DA释放会增加对该杆的偏好（图7a）。我们通过在补充图9中增加或减少向网络输入的RPE来模拟这些条件，并观察到类似的行为结果（图7b）。与以前的模拟一样，这些结果是在网络权重保持不变的情况下获得的。因此，由我们的模拟光遗传学干预引起的行为变化反映了多巴胺能RPE信号对前额叶网络内单位活动的影响，而不是对突触权重的影响。在这方面，本模拟因此提供了对实验结果的一种解释，该解释与从标准模型中得出的结果完全不同。

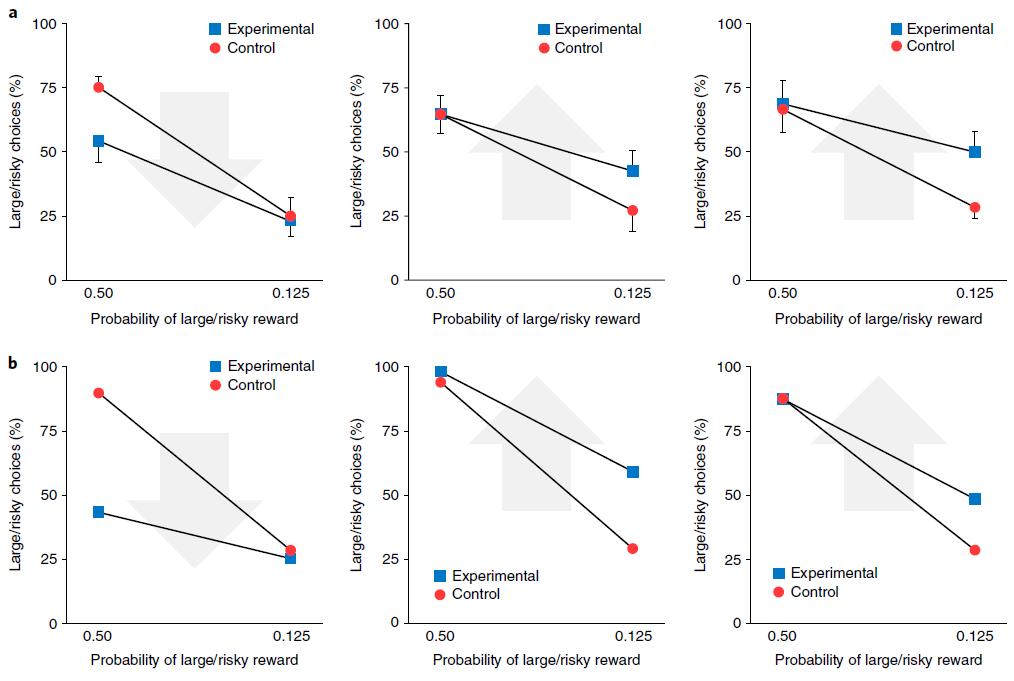
图7 | 多巴胺的双重作用：产生突触变化以进行缓慢学习，并携带有关奖励的信息以进行快速学习。a，行为数据经过Stopper et al.的许可改编⁴⁴。他们的任务是反复选择一种杆，一个杆可靠地产生小额奖励（小/确定），而另一个产生大额奖励的概率为p（大/风险）。在对照条件下，大鼠在p = 0.5时比在p = 0.125（蓝色）时更频繁地选择大/风险杆。左图，发生大/风险奖励时（n = 11）的光遗传学上阻断DA的效果。箭头指示光遗传学干预的转换方向。中心，当小/确定奖励出现时（n = 8）阻止DA的效果。右图，当大/风险奖励失败时触发DA的效果（n = 9）。所有图均表示均值±s.e.m.  b，在由Stop​​per et al.⁴⁴施加条件的情况下模拟行为，条件如a所示。

 

Functional neuroanatomy. 如我们的仿真结果所示，元RL提供了一个新的视角，通过它可以检查前额叶网络和DA系统的各自功能，以及它们在学习过程中的相互作用。正如我们已经注意到的，元RL理论的一个关键假设是前额叶网络可以理解为循环神经回路^16-18。实际上，PFC位于多个循环回路的交叉点，涉及PFC自身内部的循环连接，与其他皮质区域的连接⁴⁵，最重要的是与背侧纹状体和中腹丘脑的连接（补充图3）。普遍的观点是，在此皮质-基底节-丘脑-皮质环中纹状体的作用是通过控制信息流进入PFC电路来调节PFC的动态。据此，DA用作纹状体内的训练信号，通过时序差分学习来塑造门控函数的操作。使用这种更详细的皮质-纹状体环模型复制我们的模拟结果，是未来研究的重要目标。

　　值得注意的是，纹状体门控理论最初是由LSTM网络启发而来的，这种网络是我们在模拟中采用的那种模型（图1b）。确实，最近的工作提出了在PFC上运行的多种门控机制，它们直接与传统上在LSTM网络中实现的输入，记忆和输出门控机制并行⁴⁶（请参见方法）。尽管这些相似之处很吸引人，但也应注意，其他最新工作已使用更通用的RNN（缺少LSTM网络中涉及的门控机制）对PFC中的RL进行建模^16,18。尽管我们已经确定的元RL效应仅依赖于循环的存在，而不依赖于任何特定的门控机制，但是测试特定的门控机制是否能够为人类和动物的学习曲线和神经表征提供更精确的定量拟合将是有趣的。

　　我们在本文中考虑的神经科学数据主要集中在将背侧PFC与基底神经节连接的所谓“关联回路”中的结构上（补充图3）。但是，这只是大脑中几种此类循环回路中的一种，其他循环穿过皮质的其他区域（补充图3）。这就提出了一个问题，即其他循环回路（例如贯穿体感和运动皮层的“感觉运动回路”）是否也支持元RL。尽管我们不能排除在这些循环中也可能出现元学习形式的可能性，但我们观察到，本文描述的元RL效应只有在网络输入携带有关近期动作和奖励的信息以及网络动态支持在合适的时间段内信息的维护时才会出现。这两个因素可能使关联回路与其他皮质-基底节-丘脑-皮质回路⁴⁷不同，这解释了为什么元RL可能在该回路中独特地出现（补充图3）。
　　我们的大多数模拟都将所有PFC建模为一个没有区域专业化的单一全连接网络。但是，PFC内部存在重要的功能解剖区别。例如，在模拟1中看到的概率匹配行为和在模拟4中有模型学习模式在背外侧PFC中具有强大的神经相关性^7,11，而在模拟2中建模的不稳定性编码在前扣带回皮层中报道³⁴。尽管前扣带回和背外侧PFC的不同作用仍在争论中，但本理论的重要下一步将是考虑到元RL涉及的计算如何在这些区域中发挥作用，因为它们不同的细胞特性，内部电路和外部连接。同样重要的是位于所谓的“边缘环”中的PFC区域，包括眶额和腹侧PFC（请参见补充图3）。后者的两个区域都与奖励编码有关，而最近的工作表明，眶额皮质可能还编码了抽象的隐状态^36,37，它们都是元RL的关键函数，如我们的一些模拟所示。再次，更全面的元RL理论发展将需要更明确地纳入这些区域的相对角色。

 

Discussion

　　我们利用元RL的概念提出了有关DA和PFC在基于奖励的学习中的作用的新建议。我们先进的框架保留了DA功能的标准RPE模型，但将其置于新的环境中，使其能够重新适应以前令人费解的发现。如我们的仿真所示，元RL解释了有关DA和PFC功能的各种观察结果，为解决这两个系统的文献之间提供了桥梁。
　　除了解释现有数据外，元RL框架还带来了许多可测试的预测。如我们所见，该理论表明PFC在有模型控制中的作用至少部分是由DA驱动的突触学习引起的。如果这是正确的，则在初始训练期间干扰相位DA信号将干扰模拟4和5中研究的任务中有模型控制的出现。另一个预测涉及有模型的多巴胺能RPE信号。元RL将这些信号归因于来自前额叶网络的价值输入。如果正确，那么损害或失活PFC或其相关的纹状体核应消除有模型的DA信号⁴⁸。通过检查我们模型的前额叶网络部分中产生的活动模式，将这些模式视为执行相关任务的动物神经活动的预测器，可以指定进一步的预测。对这项工作有用的行为任务可能来自最近的工作，该工作牵涉到PFC在RL上下文中识别隐状态^19,36-38和抽象规则⁴⁹。

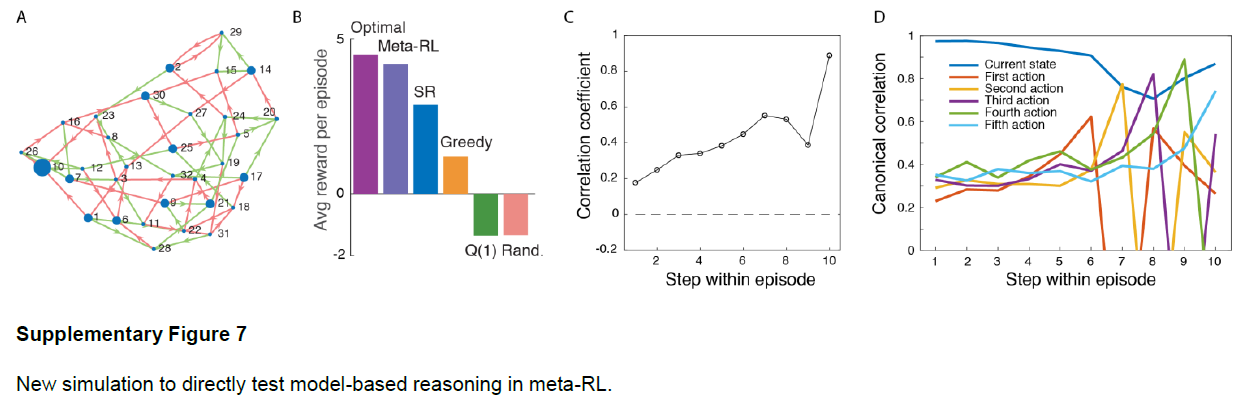
　　元RL还提出了一系列更广泛的问题，我们希望这些问题能够刺激新的实验工作。在元RL背景下，中边缘，中皮质和黑纹状体DA通路的相对作用可能是什么？元RL是否指向PFC的背侧和腹侧或内侧和外侧区域之间分工的新解释？我们应该如何解释指向支持有模型和无模型RL的系统存在的数据（补充图7和8）？当元RL与保存回合式记忆的机制接触时，会出现哪些新的动态⁵⁰？总而言之，元RL在有关基于奖励的学习的思想领域中提供了新的定位点，这可能在开发新的研究问题和解释新发现方面很有用。

 

Methods

　　可从https://doi.org/10.1038/s41593-018-0147-8中获得方法，包括数据可用性声明以及任何相关的登录号和参考文献。

 

Methods

Architecture and learning algorithm. 我们所有的仿真都采用了一套通用的方法，但实现上的变化很小。智能体架构的重点是全连接的门控RNN(LSTM：长短期记忆网络⁵¹；有关公式，参见下文)。除指定的地方外，在所有实验中，输入都包括观察值，该标量指示在前一个时间步骤上收到的奖励，以及在前一个时间步骤上采取的动作的one-hot表征。输出由标量基准(价值函数)和长度等于可用动作数的实向量组成。从该向量定义的softmax分布中采样动作。其他一些架构细节根据不同任务的结构而有所不同(参见下面的仿真特定细节)。RL是由A2C实现的，如Mnih et al.⁵²所述。Mnih et al.⁵²描述了训练的细节，包括使用熵正则化以及组合的策略和价值估计损失。简而言之，完整目标函数的梯度是策略梯度，状态价值函数损失的梯度和熵正则项的加权和，定义如下：

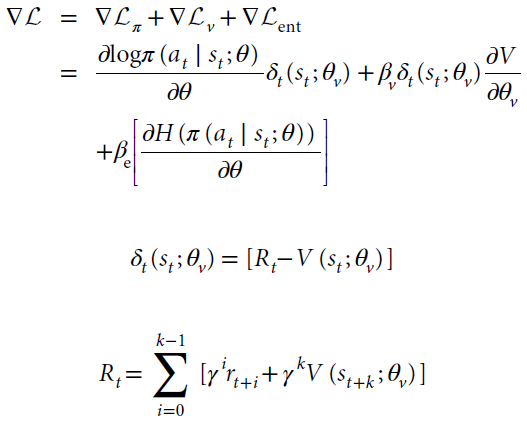
其中a_t，s_t和R_t定义了时间 t 处的动作，状态和折扣的n步自举回报(折现因子γ)，k是直到下一个终端状态的步数，且上限为最大展开长度t_max，π是策略(由神经网络参数θ参数化)，V是价值函数(由θ_v参数化)，估计状态s的期望收益，H(π)是策略的熵，β_v和β_e分别是控制价值估计损失和熵正则化项的相对贡献的超参数。δ_t(s_t; θ_v)是n步回报时序差分误差，它提供了对actor-critic的优势函数的估计。使用Mnih et al.⁵²详述的A2C，通过梯度下降和随时间的反向传播来更新神经网络的参数。请注意，尽管参数θ和θ_v被分开显示，如Mnih et al.⁵²所示，实际上，它们共享所有非输出层，并且仅在针对策略的softmax输出和针对价值函数的一个线性输出方面有所不同。仿真1–4和6使用单线程，并接收编码为one-hot矢量的离散观测值，并带有可能状态数的长度(有关单线程A2C的伪代码，请参见补充图1)。仿真5在训练期间使用了32个异步线程，并接收RGB帧作为输入(有关异步多线程算法和伪代码，请参见Mnih et al.⁵²)。核心循环网络由仿真1-4中的48个LSTM单元，仿真5中的256个单元和仿真6中的两个独立的LSTM(每个LSTM为48个单元(用于策略和价值))组成(参见补充图1)。

　　在标准的非门控RNN中，时间步骤 t 的状态是时间步骤t–1的状态的线性投影，紧跟着的是非线性。这种"普通的"RNN可能难以满足长期的时间依赖性，因为它必须学习非常精确的映射，才能将信息从一个时间状态复制到另一个时间状态。相比之下，LSTM的工作原理是将每个时间步骤的内部状态(称为"单元状态")复制到下一个时间步骤。默认情况下，它会记住，而不必学习如何记住。但是，它也可以选择使用"忘记"(或维护)门来忘记，并选择使用"输入"门来输入新信息。由于它可能不想在每个时间步骤输出其全部记忆内容，因此还有一个"输出"门来控制输出内容。这些门中的每一个都通过网络状态的学习函数进行调节。

　　更准确地说，LSTM的动态由标准公式^51,53决定：

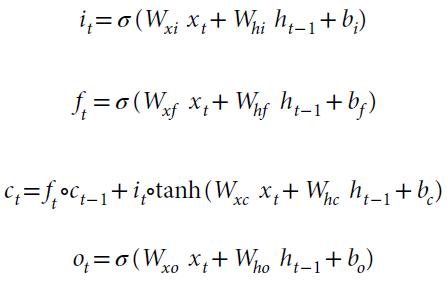
其中x_t是时间 t 到LSTM的输入，h_t是隐含状态，i_t是输入门，f_t是忘记/维护门，o_t是输出门，c_t是单元状态，σ是sigmoid函数，并且ο是表示逐元素相乘的运算符。

 

General task structure. 任务是回合式的，包括一定数量的试验(除非另有说明，否则为每回合固定数量)，任务参数是从分布中随机抽取的，并在回合持续时间内固定。在仿真1、3、4和6中，每个试验均以注视信号开始，要求一个独特的中央注视响应(a_C)，然后是一个或多个刺激信号，每个刺激信号都需要一个刺激响应(左，a_L或右，  a_R)。未能对注视或刺激信号产生有效响应的奖励为–1。在仿真5中，涉及到高维视觉输入，注视和图像选择，需要连续发出左-右动作才能将目标移动到视场中心。额外的无操作动作被提供，以允许智能体根据需要保持注视，并且对于产生无效动作也没有给予负奖励。有关更多详细信息，请参见特定于仿真的方法。

 

Training and testing. 训练和测试环境都涉及从预定的任务分布中采样任务(大多数情况下是随机采样，尽管原则上的例外情况请参见仿真1和2)，并在每个回合的开始处初始化LSTM隐含状态(仿真1-4和6学到的初始状态；为仿真5初始化为0)。除非另有说明，否则训练超参数(由Mnih et al.⁵²定义)如下：学习率=0.0007，折扣因子=0.9，状态-价值估计成本β_v=0.05和熵成本β_e=0.05。使用Shared RMSProp和通过时间的反向传播对权重进行了优化，其中涉及根据任务将循环网络展开固定数量的时间步骤(范围从t_max=100到300)，具体取决于任务，并确定计算自举n步回报时的步数。然后在测试回合评估智能体，在此期间所有网络权重保持固定。除了根据相关工作的先验经验，并没有选择看起来合理的先验值之外，没有进行任何参数优化来改进数据拟合度，并且仅进行了细微调整即可获得可靠的任务。

　　现在，我们详细介绍特定于仿真的任务设计，超参数和分析。请注意，在介绍性的双臂赌博机仿真中报告的仿真的详细信息取自Wang et al.³¹。

 

Simulation 1: Reinforcement learning in the prefrontal network. 此任务来自Tsutsui et al.⁷，要求智能体在两个动作a_L和a_R之间进行选择，其动态奖励概率会根据先前的选择而发生变化。动作的奖励概率根据下式给出：

p₀(a)的值是动作a的基准奖励概率，它是从均匀的Bernoulli分布中采样的，并在整个回合中保持固定。n(a)是自选择动作a以来的试验次数。两个臂的基准概率之和始终为常数，即0.5，因此p₀(a_L)=0.5 – p₀(a_R)。每回合的试验次数从50到100均匀变化(在回合开始时随机选择)。仅出于训练目的，我们提供了环境参数的子集p₀=0.1–0.2和0.3–0.4，因此智能体仅在p₀=[0.0–0.1]⋃[0.2–0.3]⋃[0.4-0.5]上进行了训练。对于此任务，我们使用折扣因子=0.75，并进行3×10⁶步(约15000个回合)的训练。

　　训练后，我们在固定网络权重的情况下对智能体进行了500次测试。对模型行为的分析是基于原始研究的，而原始研究又采用了Lau and Glimcher³³引入的技术。我们通过拟合逻辑斯蒂回归模型(如Lau and Glimcher³³和Tsutsui et al.⁷所做的)确定了过去的选择和奖励结果对逐项试验响应的影响，最大试验滞后时间为N=15。为了将我们的分析限制在稳态行为之内，我们考虑了每个回合的最后三分之二。

　　为了评估循环网络中每个变量的编码信息量，我们计算了隐含单元激活与四个因素之间的Spearman偏秩相关性：最近动作，最近奖励，动作×奖励交互和选择价值。(请注意，我们的任务实现对动作和目标对象之间的区别进行了抽象，并且我们不关注动作和对象价值之间的区别。)因为这两个动作的价值是高度反相关的(r=–0.95，Pearson相关)，我们只考虑了左动作的效果。

 

Simulation 2: adaptation of prefrontal-based learning to the task environment. 在每个步骤中，智能体在a_L和a_R这两个动作之间进行选择，并获得R或0的奖励。获得的R的大小可以在试验之间随机变化且在两个动作之间独立(分布为100×β(4, 4))，并在每次试验中都提示给智能体。两臂的回报概率完全反相关，因此由随时间变化的单个参数r(t)来描述。在测试中，r(t)的演变反映了人类受试者在Behrens et al.³⁴中执行的任务。这里有两种类型的回合。首先，在低波动的回合中，对于100次试验，r(t)保持稳定在0.25或0.75，然后每25次试验在0.2和0.8之间交替。在高波动性回合中，对于100次试验，每25次试验r(t)在0.2和0.8之间交替，然后保持稳定在0.25或0.75。

　　为了进行训练，我们改编了Behrens et al.³⁴用于推断的两级生成模型。具体来说，在训练中，r(t)根据v(t)演化，因此概率为v(t)，r(t+1)设置为1 – r(t)，概率为1 – v(t)，r(t+1)保持与r(t)相同。类似地，波动率v(t)也随时间演变。概率为k时，v(t+1)设置为0.2 – v(t)；概率为1 – k时，v(t+1)保持与v(t)相同，其中log(k)在每个回合的末尾介于–4.5和–3.5之间均匀采样。在每个训练回合开始时，将v(1)随机初始化为0或0.2。当v(t)为0时，r(t)设置为0.25或0.75，而当v(t)为0.2时，r(t)设置为0或1。这种方式与Behrens et al.³⁴中执行的任务主体的结构相匹配(参见上文和图3a)。在该研究中采用的概率模型没有强加这种联系，其结果是学习率的动态调整对期望奖励的影响较小。为了完整起见，我们还进行了仿真，其中使用Behrens et al.³⁴所用生成模型产生的数据对元RL进行了训练，并获得了定性相似的结果(数据未显示)。

　　对元RL进行了40000个回合的训练，并测试了400个回合，每个回合包括200次试验。由于这些回合的长度，我们不包括注视步骤。进行训练时，学习率=5×10^-5，折扣=0.1，并且在训练过程中，熵成本从1线性减少到0。与所有仿真一样，权重在测试中保持固定。

　　为了进行分析，根据Behrens et al.³⁴，我们实现了贝叶斯智能体，该贝叶斯智能体在定义训练经验的生成模型下执行了最优概率推断。贝叶斯智能体使用后验的离散表征，如Behrens et al.³⁴。我们报告的"估计波动率"信号是在时间 t 处智能体的期望波动率。我们还拟合了多元回归模型，以从循环网络的隐含激活中预测每个时间步骤的贝叶斯智能体估计的波动性，并将此模型应用于延迟回合(交叉验证)中的隐含激活，以生成报告给元RL的"解码波动性"信号。

　　仅根据LSTM和贝叶斯的行为，也估计了它们的学习率。为了估计学习率，我们以最大似然将Rescorla-Wagner模型拟合到行为。两种类型的回合(先高波动率和先低波动率)分别拟合。Rescorla–Wagner模型适合所有回合的行为，但仅从连续10次试验开始，以单次试验增量滑动10次试验的窗口，以观察学习率如何动态变化。尽管只有十个连续的试验直接影响了可能性，但是在这十个试验之前的所有试验都是通过其对逐步形成的价值估计的影响而间接贡献的。作为对照，我们估计了具有固定学习率的Rescorla-Wagner模型生成的行为的学习率，以确保我们能够在没有偏差的情况下恢复真实的学习率。

　　为了确定编码为波动率的隐含单位的比例，在每个回合中，我们将每个隐含单位的活动相对于真实波动率进行了回归(编码为0或1)。(此回归模型还包括多个协变量：先前的奖励，下一个动作和在当前时间步骤上获得奖励的真实概率。但是，包括这些协变量对发现为编码波动率的单位比例的影响很小。)然后我们计算了波动率回归斜率显著不同于零(在P=0.05的阈值时)的单位，Bonferroni校正了隐含单位。该数字的平均值和标准误差在正文中报告。

　　在类似的分析中，我们还在每个时间步骤上对回合进行了回归。在补充图5a中，我们绘制了在Bonferroni校正阈值P=0.05时，波动率回归变量的斜率显著不同于零的单位比例。在补充图5b中，我们在很宽的范围内不断改变阈值，并绘制了超过试验阈值的平均比例(按试验平均)。

　　最后，我们注意到Behrens et al.³⁴使用贝叶斯模型估计的波动率信号作为回归变量，而我们使用的是真实波动率。我们发现这两种方法没有产生质的不同结果。但是，以细粒度的单个试验来解释贝叶斯估计的波动率信号稍微困难些，因为贝叶斯估计的信号对单个试验事件敏感。特别是在回合初期，贝叶斯估计信号更多地反映了已收到的特定结果，而不是波动性。

 

Simulation 3: reward prediction errors reflecting inferred value. 按照Bromberg-Martin et al.¹²的要求，我们在反转任务上对智能体进行了训练，其中两个刺激信号的价值是反相关的，一个被奖励而另一个未被奖励。奖励的刺激以无提示的方式间歇地切换，因此在每个回合开始时有50％的机会进行切换。具体而言，在步骤1进行中央注视信号后，在步骤2中向智能体显示了两个刺激信号(表格式one-shot矢量)之一，指示它必须在第3步产生左动作(aL)或右动作(aR)。然后在第4步交付奖励，随后开始下一个试验。如果在任何步骤上均未产生有效的响应，则将获得–1的奖励，而如果执行有效的动作，则将对奖励的信号提供1的奖励，而对于未奖励信号和中央注视信号则提供0的奖励。

　　在回合开始时随机确定有奖励和无奖励的信号，并在回合持续时间内保持固定，持续5次试验(20个步骤)。使用200步的反向传播窗口训练2×10⁶步或1×10⁵个回合后，我们测试了1200个回合，并针对试验1和2的刺激表现(步骤2)计算了奖励预测误差：

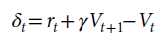
还从步骤1和3中提取了基准(即相应的V_t)进行比较。我们分析了相对于前一个回合发生了奖励反转的所有测试回合。

 

Simulation 4: ‘model-based’ behavior—the two-step task. 两步任务的结构(图5a)直接基于Miller et al.³⁹使用的版本。中心固定后，在试验的第一阶段，智能体选择a_L或a_R并转换为两个第二阶段状态S₁或S₂中的一个，概率为p(S₁|a_L)=p(S₂|a_R)=0.8 ("常见"转换)，并且p(S₁|a_R)=p(S₂|a_L)=0.2 ("罕见"转换)。转换概率p在各个回合之间是固定的。状态S₁和S₂根据[p(r|S₁), p(r|S₂)]=[0.9, 0.1]或[0.1, 0.9]产生概率奖励，在每次试验开始时，特定的奖励意外事件有2.5％的机会随机切换。对该智能体进行了100个试验的10000个回合的训练，并在固定权重的300个额外回合进行了测试。行为分析(图5c, e)严格遵循Miller et al.³⁹和Daw et al.¹⁵规定的相应程序。

　　为了将我们的元RL智能体的RPE与通过无模型和有模型的算法生成的RPE进行比较，我们遵循Daw et al.¹⁵所采用的程序。在该研究中，参考的无模型算法为SARSA(0)，有模型算法为前瞻性计划者，两者均由Daw et al.¹⁵实现。但是，代替在第二个阶段执行Q学习(这不是最优的)，有模型算法跟踪隐变量H来描述p(r|S₁)是否为0.9 (等于p(r|S₂)是否为0.1)。利用对任务真实结构的了解，该算法根据每个结果更新了对H的信念。两种算法都应用于元RL智能体经历的相同试验序列。如Daw et al.¹⁵所述，每个智能体在每个步骤上都会产生奖励预测误差，但是如果第二阶段的奖励期望为p(H)×0.9 + (1 - p(H))×0.1，智能体处于状态S₁，并且如果智能体处于状态S₂，则(1 - p(H))×0.9 + p(H)×0.1。

　　按照仿真3计算元RL的RPE。我们对确定元RL的RPE是仅有模型的，仅无模型的还是二者的混合。这种分析必须考虑到以下事实：无模型的和有模型的RPE本身在某种程度上是相关的(补充图6)。我们首先将元RL的RPE直接与前瞻性计划者有模型的RPE进行了回归。找到几乎完美的相关性之后，我们询问元RL的RPE是否和与有模型的RPE正交的无模型RPE的组件有关。为此，我们通过将有模型的RPE从无模型的RPE中回归出来，并寻找元RL的RPE与残差之间的相关性。我们注意到，与Daw et al.¹⁵在功能性磁共振成像研究中所研究的主题不同，我们的模型显示了纯粹有模型的行为模式(见图5c, e)。相应地，在本分析中，我们发现仅有模型的RPE。作为验证性分析，我们还使用元RL的RPE作为因变量，将有模型的RPE和无模型的RPE都作为自变量进行了多元回归(补充图6)。

 

Simulation 5: learning to learn. Wang et al.³¹提出了该仿真的早期版本。为了仿真Harlow的40个学习任务，我们使用Psychlab框架⁵⁴用RGB像素输入来训练智能体。一个84×84像素的输入代表一个模拟的计算机屏幕(参见图6a和补充视频1)。在每个试验开始时，该显示为空白，除了一个小的中央固定叉。智能体选择了离散的左-右动作，这些动作在相应的方向上将其视线移动了约4.4度，并且动量效应较小(或者，可以选择无操作动作)。要完成试验，需要执行两项任务：扫描到中央注视交叉点，然后扫描到正确的图像。如果智能体将注视交叉点保持在视场中心(视角范围为3.5度以内)至少四个时间步骤，则得到的奖励为0.2。然后，固定十字消失了，从ImageNet数据集⁵⁵随机抽取并调整为34×34的两个图像分别出现在显示器的左侧和右侧(图6a)。然后，智能体的任务是通过旋转直到图像的中心与视场的中心对齐(在7度视角范围内)来"选择"其中一幅图像。一旦选择了其中一张图像，两张图像都消失了，在间隔10个时间步骤之后，重新出现了固定十字，开始了下一次试验。每个回合最多包含六个试验或3600个步骤。强制将每个选定的动作重复进行总共四个时间步骤(如Mnih et al.[52]所示)，这意味着在完成注视后，选择图像至少要进行三个独立的决定(十二个原始动作)。但是，应当注意的是，智能体的旋转位置不受限制。也就是说，可能会发生360度旋转，而模拟的计算机屏幕只能对向65度。

　　尽管在每个回合的开头选择了新的ImageNet图像(从一组1000张图像中进行替换采样)，但相同的两个图像在一个回合中的所有试验中都可以重复使用，尽管其左右位置随机变化，类似于Harlow⁴⁰实验中的对象。就像在该实验中一样，在整个回合中，任意选择一张图片作为"奖励"图片。选择此图像产生的奖励为1.0，而另一张图像产生的奖励为–1.0。LSTM使用100步展开的时间反向传播进行训练。

　　在测试过程中，网络权重保持固定(在卷积网络和LSTM-A3C中)，而ImageNet图像则是从一个单独且不包含在训练过程中的1000张图片中抽取的。通过将回合回报取滚动平均值并从0到100％归一化来计算每个副本的学习曲线，其中50％表示在两个图像之间随机选择的性能，而100％表示最优性能。我们使用了Wang et al.³¹中采用的超参数训练了50个网络(学习率=0.00075，折扣=0.91，熵成本β_e=0.001，状态价值估计成本β_v=0.4)，发现28％在〜1x10⁵个回合之后达到了最优性能(每个线程，32个线程)。因为此任务不仅需要学习抽象的规则结构，而且还需要处理视觉上复杂的图像，保持面向模拟计算机屏幕的方向和中央注视，所以大部分初始训练时间都花在了0％的性能上。最终，成功的智能体在克服这些初始障碍所需的回合次数上有所不同(中位数3413，范围1810–29080)。为了表征与这些其他考虑因素分离的抽象任务结构的获取，我们在学习曲线中确定了两个变化点(达到偶然水平的性能和逼近最高性能)，并在这些变化点(六个分位数)之间插值的各种性能分位数以及训练结束时的最终性能中，绘制了平均奖励作为回合内试验次数的函数。智能体在达到偶然水平的性能后达到最高性能所需的回合数量也有所不同(中位数4875，范围1500-82760)。

　　为了确保元RL网络能够真正执行Harlow⁴⁰任务要求的角色填充任务分配，而不是依靠更简单的策略，我们在Harlow⁴⁰任务的变体中训练了相同的模型，其中在整个试验中，非目标(无奖励)图像发生了变化，始终采用不熟悉的图片形式。经过训练后，我们网络的性能与原始任务中的性能相同，第一个试验的偶然准确度随后为同一试验块其余部分的接近上限的准确度(数据未显示)。

 

Simulation 6: the role of dopamine—effects of optogenetic manipulation. 我们执行了Stopper et al.⁴⁴中所述的概率风险/奖励任务，受试者在始终提供小额奖励(r_S=1)的"安全"臂或提供大额奖励(r_L=4)的"风险"臂之间进行选择，在回合开始时进行采样的概率为p(a_large)=0.125 (Safe Arm Better block)或0.5 (Risky Arm Better block)。与最初的研究直接相似，首先要求该智能体对每个安全和有风险的臂(随机配对)进行5次强制选择，然后进行20次自由选择。风险和安全臂的位置(即相关动作)可以在回合之间切换，概率为0.5。

　　为了模拟光遗传学刺激，有必要实现我们原始架构的一种变体，其中两个独立的LSTM(每个48个单位)模型价值估计和策略(而不是具有两个线性输出的单个LSTM)，并和与基底神经节和PFC功能相关的标准actor/critic架构保持一致(参见补充图3)。具体而言，将critic建模为LSTM，该LSTM将状态观察值，最后获得的奖励和最后采取的动作作为输入，输出价值估计。actor接收状态观察，最后采取的动作以及根据从critic输出的价值估计计算出的奖励预测误差，然后输出策略(参见补充图9)。由于RPE是根据前额叶网络价值输出计算得出的，因此在我们给出其他结构和算法假设的情况下，RPE不能作为critic的输入。

　　通过控制输入到actor中的奖励预测误差值来模拟光遗传学刺激，这与Stopper et al.⁴⁴直接比较了外侧缰核和腹侧被盖区刺激。在将正常RPE输入到actor的控制条件下训练了我们的智能体之后(4×10⁶步；每个实验进行了6.67×10⁴个回合，每个回合共30个试验)，我们在四种不同的条件下测试了我们的智能体共1333个回合，旨在近似Stopper et al.⁴⁴所采用的不同的刺激规程：(1) 控制(类似于Stopper的基准无刺激条件），(2) 阻止风险奖励——如果选择并奖励了风险分支，则从RPE中减去4(近似外侧缰核刺激)(4个脉冲序列)，(3) 阻止安全奖励——如果选择了安全臂，则从RPE减去1(用1个脉冲序列近似对外侧缰核刺激)，以及(4) 阻止风险损失——如果风险臂被选择而没有奖励，给RPE加1的奖励(近似腹侧被盖区刺激)。

 

Statistics. 除非另有说明，否则我们在仿真中报告的方差与相应的人类或动物实验中的方差平行时，将运行n = 8个仿真副本。除了具有不同的随机种子之外，所有副本都是相同的。我们报告了这些副本的差异，并认为这与动物实验最具有可比性。每个副本还包含许多回合，这些回合用于执行详细分析，以便与人类和动物数据进行比较。 在执行此操作的地方，其他运行产生了非常相似的结果模式。

　　我们报告均值和s.e.m. 除非另有说明，否则贯穿本文。除非另有说明，否则相关性都是Pearson's r。除非另有说明，否则所有测试均为two-tailed。假定数据分布正常，但是尚未经过正式测试。除非另有说明，否则没有数据点被排除在分析之外。没有使用统计方法来确定样本数量，因为所有网络都可以进行充分的性能训练。数据收集和分析不是盲目的实验条件，因为这不适用于我们的仿真。数据收集和分配给实验组也不适用，因为所有网络在训练之前都是等效的。

 

Reporting Summary. 有关实验设计的更多信息，请参见《自然研究报告摘要》。

 

Code and data availability. 数据共享不适用于本研究，因为未生成或分析任何实验数据集，但根据要求，通讯作者可提供来自仿真1–6的模型训练版本的行为和激活数据以及分析脚本的开源版本。

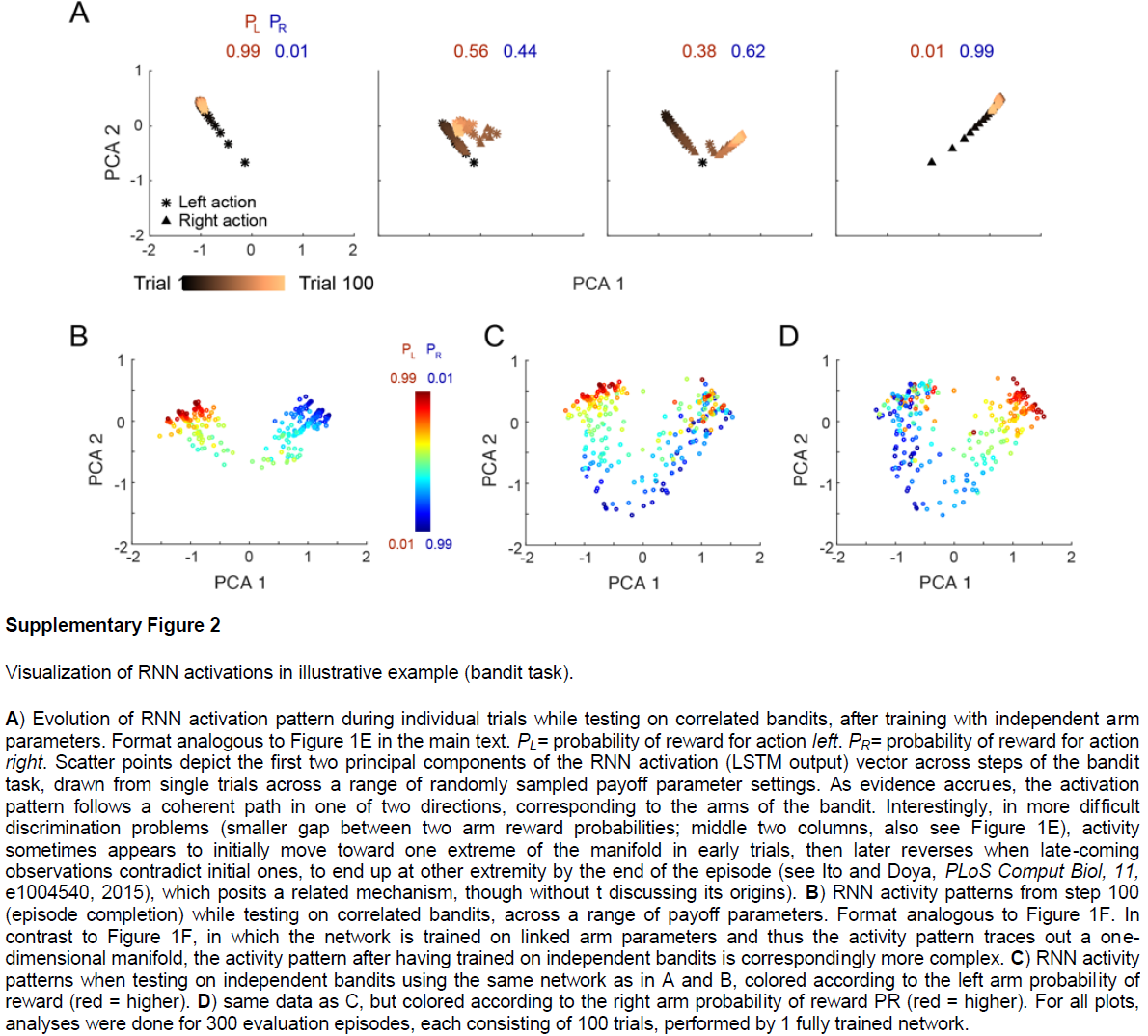
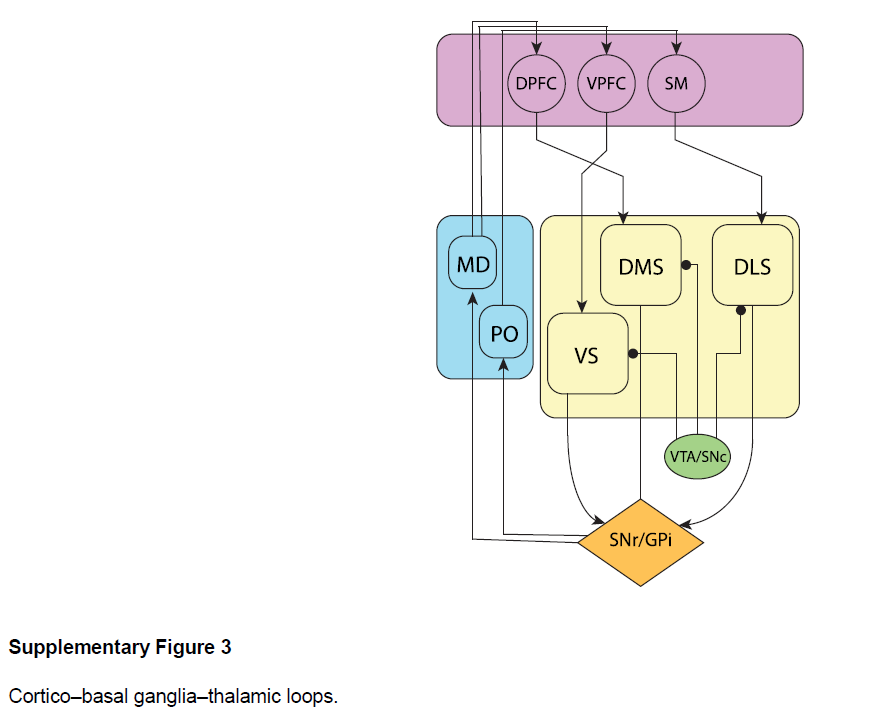
　　如主要论文所述，我们称为前额叶网络的RNN不仅包括PFC本身，眶额叶，腹侧额叶，扣带状，背外侧前额叶和额极区，还包括了其最强烈的皮层下结构连接(包括腹侧纹状体，背侧纹状体(或其灵长类同源物)和腹中丘脑)。因此，我们假设的循环连接不仅是前额叶皮层本身固有的，而且还跨越了平行的皮层-基底神经节-丘脑环路。该图基于Glimcher, P. W., ＆ Fehr, E. (Eds.). (2013). Neuroeconomics: Decision making and the brain. Academic Press, page 278. 绘制了这些环路的标准模型。DPFC：背侧前额叶皮层，包括背外侧前额叶和扣带状皮层。VPFC：腹侧前额叶皮层，包括腹内侧和眶额前额叶皮层。SM：(Somato-)感觉运动皮层。VS：腹侧纹状体。DMS：背侧纹状体。DLS：背外侧纹状体。VTA/SNc：腹侧被盖区和黑质致密部，圆形箭头指示多巴胺能投射。SNr/GPi：网状黑质/苍白球(Substantia nigra pars reticulate/Globus pallidus pars interna)。MD：背内侧丘脑。PO：后丘脑。通过DPFC运行的电路被称为"关联环路"。通过VPFC的电路称为"边缘环路"；电路通过SM作为"感觉运动环路"运行(Haber, S., Neuroscience, 282, 248-257, 2014)。

　　组织PFC各个区域和纹状体相关区域功能的一种方法是，参考RL研究中引入的actor-critic结构，腹侧区域扮演critic角色(计算价值函数的估计)，而背侧区域扮演actor的角色(实施策略；参见Botvinick, M. M., Niv, Y.＆Barto, A. C., Cognition, 113, 262-280, 2009, and Joel, D., Niv, Y.＆Ruppin, E., Neural Networks, 15, 535-547, 2002)。我们对前额叶网络输出的假设包括价值估计和动作，这并非巧合。从这个意义上讲，我们正在根据actor-critic架构来概念化前额叶网络，并且通过引入有关神经解剖结构和actor-critic架构之间映射关系的现有思想，对该范式的进一步阐述可能会实现更细粒度的结构差异(参见，例如Song, H. F., Yang, G. R.＆Wang, X.-J., eLife, 6, e21492, 2017)。我们在仿真6中引入的实现朝着这个方向迈出了一步，将前额叶网络分为两半，在功能上对应于actor和critic。

　　优化我们的网络时使用的损失函数包括价值回归和策略梯度的术语。Actor-critic模型表明，皮层和基底神经节非常类似于这两种损失(例如，Joel, Niv＆Ruppin, Neural Networks, 15, 535-547, 2002)。随着多巴胺预测误差将价值估计推向目标，人们认为价值回归在基底神经节中得以实现(Montague, Dayan＆Sejnowski, Journal of Neuroscience, 16, 1936-1947, 1996)。同时，策略梯度损失只是增加了参与产生动作的联系的强度(当该动作产生正奖励时)，这被认为是多巴胺在皮层纹状体突触中充当可塑性调节器的作用。

　　在元RL理论下，DA在调节突触功能中的作用应仅在相对较长的时间范围内发挥作用，从而在多个任务过程中塑造前额叶动态。这与标准模型相反，该模型假定DA可以足够快地驱动突触变化，从而在几秒钟的时间内影响行为。有趣的是，尽管进行了数十年的深入研究，但尚无直接证据表明阶段性DA信号可迅速推动突触改变。的确，我们没有实验证据表明，DA浓度跨度小于一整分钟的阶段性升高可以显著影响突触功效，并且在许多研究中，DA阶段性波动的影响可能需要几分钟(甚至数十分钟)才能上升(Brzosko, Z., Schultz, W.＆Paulsen, O., Elife, 4, e09685, 2015; Otmakhova, NA＆Lisman, J. E., Journal of Neuroscience, 16, 7478-7486, 1996; Yagishita, S. et al., Science, 345, 1616-1620, 2014)。缺乏有关阶段性DA对突触可塑性更快影响的证据，这为标准模型带来了另一难题。相比之下，元RL框架直接预测前额叶网络中实际上不应存在DA的这种短期效应，并且在该网络中，阶段性DA信号传导对突触功效的影响应该在更长的时间范围内起作用。