A Distributional Perspective on Reinforcement Learning

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

 

arXiv:1707.06887v1 [cs.LG] 21 Jul 2017

In International Conference on Machine Learning (2017).

 

Abstract

　　在本文中，我们争论了价值分布的根本重要性：强化学习智能体获得的随机回报的分布。这与强化学习的通用方法形成对比，后者是对这种回报或价值的期望进行建模的方法。尽管已有大量研究价值分布的文献，但迄今为止，它一直被用于特定目的，例如实现风险意识行为。我们从策略评估和控制设置方面的理论结果开始，揭示了后者中的重大分布不稳定性。然后，我们使用分布的观点来设计一种新算法，该算法将Bellman方程应用于近似价值分布的学习。我们使用Arcade学习环境中的游戏套件评估算法。我们同时获得了最新结果和坊间证据，这些证据证明了价值分布在近似强化学习中的重要性。最后，我们结合理论和经验证据来强调在近似设置中价值分布影响学习的方式。

 

1. Introduction

　　强化学习的主要宗旨之一是，当动作不受其他方式的约束时，智能体应努力最大化期望效用Q或价值（Sutton＆Barto, 1998）。Bellman方程根据随机转换(x, a) → (X', A')的期望回报和期望结果简洁地描述了该价值：

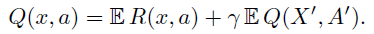
 　　在本文中，我们的目标是超越价值观念，并主张采用分布观点来进行强化学习。具体来说，我们研究的主要对象是期望价值为Q的随机回报Z。此随机回报也由递归方程描述，但具有分布性质：

分布Bellman方程指出，Z的分布以三个随机变量的相互作用为特征：奖励R，下一个状态-动作(X',  A')及其随机回报Z(X', A')。与众所周知的情况类似，我们将此数量称为价值分布。
　　尽管分布的观点几乎与Bellman方程本身一样古老（Jaquette, 1973；Sobel, 1982；White, 1988），但到目前为止，在强化学习中，它已经服从于特定的目的：对参数不确定性建模（Dearden et al., 1998），设计风险敏感算法（Morimura et al., 2010b;a）或进行理论分析（Azar et al., 2012；Lattimore＆Hutter, 2012）。相比之下，我们认为价值分布在强化学习中起着核心作用。

 

Contraction of the policy evaluation Bellman operator. 根据Rösler（1992）的结果，我们表明，对于固定策略，价值分布的Bellman算子是Wasserstein（也称为Kantorovich或Mallows）度量的最大形式的压缩。我们对度量的特定选择很重要：同一算子不是总变化量，Kullback-Leibler散度或Kolmogorov距离的压缩。

 

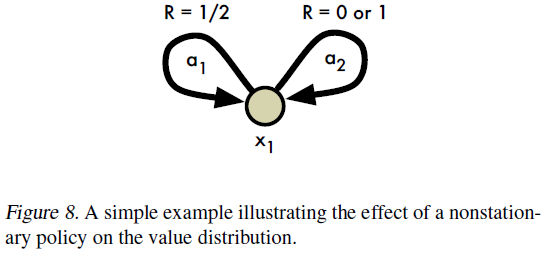
Instability in the control setting. 与策略评估案例相比，我们将证明Bellman最优方程的分布版本不稳定。具体而言，尽管最优算子是期望价值的压缩（与通常的最优结果匹配），但它并不是分布上任何度量的压缩。这些结果提供了支持对非平稳策略的影响进行建模的学习算法的证据。

 

Better approximations. 从算法的角度来看，学习近似分布而不是近似期望有很多好处。分布Bellman算子保留了价值分布的多模态，我们相信这会导致更稳定的学习。逼近全部分布还可以减轻从非平稳策略中学习的影响。整体而言，我们认为这种方法使近似强化学习的行为表现得更好。

　　我们将在Arcade学习环境（Bellemare et al. 2013）的背景下说明分布视角的实际好处。通过对DQN智能体（Mnih et al., 2015）中的价值分布进行建模，我们在基准Atari 2600游戏的整个范围内获得了显著的性能提高，并且实际上在许多游戏上都达到了最先进的性能。我们的结果与Veness et al.（2015）的结果相呼应，他通过预测蒙特卡洛的回报获得了极其快速的学习。
　　从监督学习的角度来看，学习完整的价值分布似乎是显而易见的：为什么将自己限制在均值？当然，主要区别在于在我们的环境中没有给定的目标。取而代之的是，我们使用Bellman方程使学习过程易于处理。正如Sutton＆Barto（1998）所说，我们必须“从猜测中学习猜测”。我们相信，这种猜测最终带来的好处多于成本。

 

2. Setting

　　我们考虑一个智能体以一种标准的方式与环境进行交互：在每个步骤中，智能体都会根据其当前状态选择一个动作，环境会以奖励和下一个状态对此动作做出响应。我们将此交互建模为时间同质的马尔可夫决策过程（X, A, R, P, γ）。通常，X和A分别是状态空间和动作空间，P是转换内核P(· | x, a)，γ∈[0, 1]是折扣因子，R是奖励函数，在本文中，我们将其明确视为随机变量。固定策略π将每个状态x∈X映射到动作空间A上的概率分布。

 

2.1. Bellman's Equations

　　回报Z^π是沿着智能体与环境互动的轨迹所获得的折扣奖励的总和。策略π的价值函数Q^π描述了从状态x∈X采取动作a∈A，然后根据π获得的期望回报：

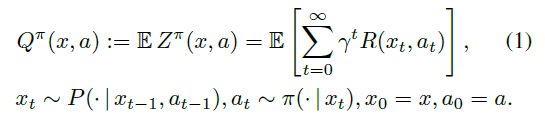
　　强化学习的基础是使用Bellman方程（Bellman, 1957）来描述价值函数：

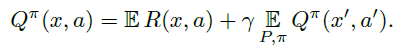
　　在强化学习中，我们通常感兴趣的是采取动作使回报最大化。最常见的方法是使用最优方程：

　　该方程具有唯一的不动点Q*，即最优价值函数，对应于最优策略集π*（当时，π*是最优的）。

　　我们将价值函数视为中的向量，并将期望奖励函数也视为这样的向量。在这种情况下，Bellman算子T^π和最优算子T如下：

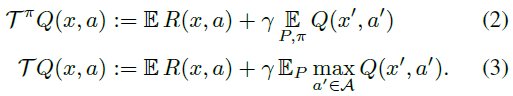
　　这些算子非常有用，因为它们描述了流行的学习算法（例如SARSA和Q-Learning）的期望行为。特别地，它们都是压缩映射，并且它们在某些初始Q₀上的重复应用分别以指数形式收敛到Q^π或Q*（Bertsekas＆Tsitsiklis, 1996）。

 

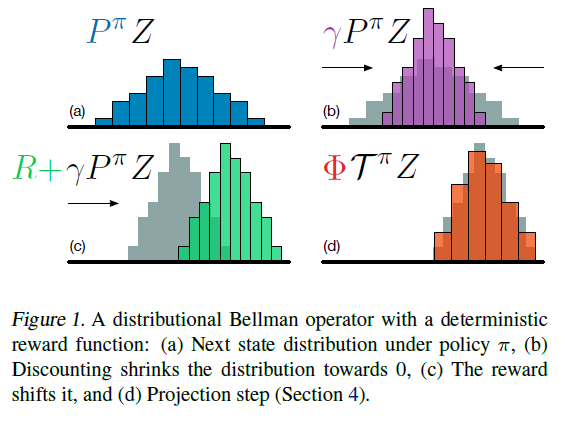
3. The Distributional Bellman Operators

　　在本文中，我们去掉了Bellman方程内的期望，而是考虑随机变量Z^π的完整分布。从这里开始，我们将Z^π视为状态-动作对到回报分布的映射，并将其称为价值分布。
　　我们的第一个目标是要了解Bellman算子的分布模拟的理论行为，尤其是在不太容易理解的控制环境中。对算法贡献严格感兴趣的读者可以选择跳过此部分。

 

3.1. Distributional Equations

　　分布方程表示随机变量U根据与V相同的密度分布。在不失一般性的前提下，读者可以将分布方程的两侧理解为与两个独立随机变量的分布相关。分布方程已被Engel et al.（2005）；Morimura（2010a）用于强化学习以及White（1988）的运筹学。

 

注：inf：下确界；ess sup（essential supermum，本质上确界）：https://blog.csdn.net/qianhen123/article/details/41845837

 

3.2. The Wasserstein Metric

　　我们进行分析的主要工具是累积分布函数之间的Wasserstein度量d_p（例如，参见Bickel＆Freedman, 1981，在此称为Mallows度量）。对于F，G在实数上的两个累积分布函数，其定义为：

其中，对所有分别具有累积分布F和G的随机变量对（U, V）求下确界。通过随机变量U的逆累积分布函数变换获得的下确界均匀分布在[0, 1]中：

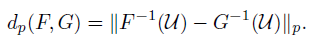
对于p < ∞，这可以更明确地写为：

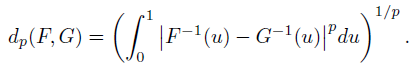
　　给定两个随机变量U，V，其累计分布函数为F_U，F_V，我们将其写作dp(U, V) := dp(F_U, F_V)。我们会发现将考虑下的随机变量与其在下确界中的版本进行合并很方便，写作：

当其是明确的；我们认为，更大的可读性证明了技术上的不准确性。最后，我们使用相应的L_p范数将此度量扩展到随机变量的向量，例如价值分布。
　　考虑一个标量a和一个与U，V独立的随机变量A。度量d_p具有以下属性：

　　我们将需要以下额外属性，该属性不对其变量进行独立假设。附录中给出了它的证明以及以后的结果。

 

3.3. Policy Evaluation

　　在策略评估设置中（Sutton＆Barto, 1998），我们对与给定策略相关联的价值函数V^π感兴趣。这里的类似物是价值分布Z^π。在本节中，我们表征Z^π并研究策略评估算子T^π的行为。我们强调，Z^π描述的是智能体与其环境互动的固有随机性，而不是某种程度的环境本身不确定性。
　　我们将奖励函数视为随机向量，并定义了转换算子：

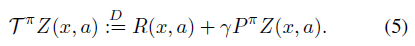
尽管T^π与通常的Bellman算子（2）具有表面相似之处，但本质上是不同的。特别地，随机性的三个来源定义了复合分布T^πZ：

1. 奖励R中的随机性；
2. 转换P^π中的随机性；
3. 下一个状态-价值分布Z(X', A')。
   

特别是，我们通常假设这三个量是独立的。在本节中，我们将显示（5）是一个压缩映射，其唯一不动点是随机回报Z^π。

 

3.3.1. CONTRACTION IN 

 

3.3.2. CONTRACTION IN CENTERED MOMENTS

 

3.4. Control

　　到目前为止，我们已经考虑了固定策略π，并研究了其关联算子T^π的行为。现在，我们着手了解控制设置的分布算子——我们在其中寻求最大价值的策略π——以及最优价值分布的相应概念。与最优价值函数一样，该概念与最优策略紧密相关。但是，尽管所有最优策略都获得相同的价值Q*，但在我们的案例中却出现了一个困难：通常存在许多最优价值分布。
　　在本节中，我们表明Bellman最优算子的分布类似物在较弱的意义上收敛于最优价值分布的集合。但是，此算子在分布之间的任何度量上都不是压缩，并且通常比策略评估算子更加反复无常。我们认为，我们在此处概述的收敛性问题是贪婪更新固有的不稳定性的征兆，例如，Tsitsiklis（2002）和最近的Harutyunyan et al.（2016）。

　　令π*为最优策略集。我们首先描述最优价值分布的含义。

 

4. Approximate Distributional Learning

　　在本节中，我们提出一种基于分布Bellman最优算子的算法。特别是，这需要选择一个近似分布。尽管以前曾考虑过高斯案例（Morimuraet al., 2010a；Tamar et al., 2016），但据我们所知，我们是第一个使用丰富的参数分布类的人。

 

4.1. Parametric Distribution

　　我们使用利用和参数化的离散分布，对价值分布进行建模，其中支持(support)是原子(atom)集。从某种意义上说，这些原子是我们分布的“规范回报”。原子概率由参数模型给出：

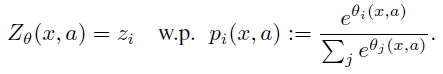
离散分布的优点是高度表达和计算友好（例如参见Van den Oord et al., 2016）。

 

4.2. Projected Bellman Update

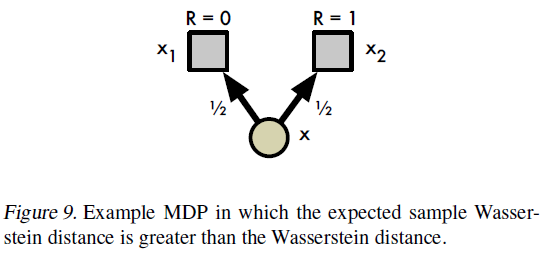
　　使用离散分布会带来一个问题：Bellman更新TZ_θ和我们的参数化Z_θ几乎总是具有不相交的支持。从第3节的分析来看，将TZ_θ与Z_θ之间的Wasserstein度量（视为损失）最小化似乎是很自然的，方便地解决支持差异。但是，第二个问题阻止了这种情况：在实践中，我们通常仅限于从样本转换中学习，这在Wasserstein损失下是不可能的（请参阅附录5和toy结果）。 

　　取而代之的是，我们将样本Bellman更新投影到Z_θ的支持上（图1，算法1），有效地将Bellman更新减少到多类别分类。令π为关于的贪婪策略。给定样本转换(x, a, r, x')，对于每一个原子 z_j 我们计算Bellman更新，然后将其概率分配给的直接邻居。投影更新的第 i 个组成部分为：

其中将其参数限制在[a, b]。¹和往常一样，我们将下一状态分布视为由固定参数参数化。样本损失是KL散度的交叉熵项：

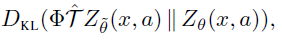
这很容易被最小化，例如，使用梯度下降。我们称这种分布和损失的选择为分类算法。当N = 2时，一个简单的单参数替代为；我们称其为伯努利算法。我们注意到，尽管这些算法似乎与Wasserstein度量无关，但最近的工作（Bellemare et al., 2017）暗示了更深的联系。

¹算法1以N为单位的时间线性计算这个投影。

 

¹算法1以N为单位的线性时间计算此投影。 

 

5. Evaluation on Atari 2600 Games

　　为了理解复杂环境下的方法，我们将分类算法应用于街机学习环境中的游戏（ALE；Bellemare等人，2013）。虽然ALE是确定性的，但随机性确实存在于许多方面：1）来自状态混叠，2）从非平稳策略学习，以及3）从近似误差。我们使用了5个训练游戏（图3）和52个测试游戏。 

　　对于我们的研究，我们使用DQN架构（Mnih et al., 2015），但是输出原子概率p_i(x, a)而不是动作-价值，并从训练游戏的初步实验中选择V_MAX = -V_MIN = 10 。我们称结果架构为分类DQN。用L_x,a(θ)代替平方损失，并训练网络以最小化此损失。²与DQN中一样，我们对期望动作-价值使用简单的ε-贪婪策略；我们将智能体可以基于全部分布选择动作的许多方式留作未来的工作。我们其余的训练方式与Mnih et al.相同，包括对使用目标网络。

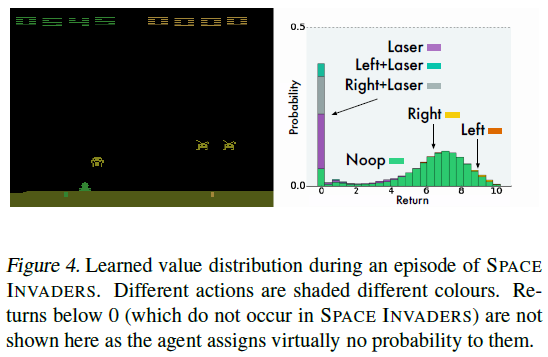
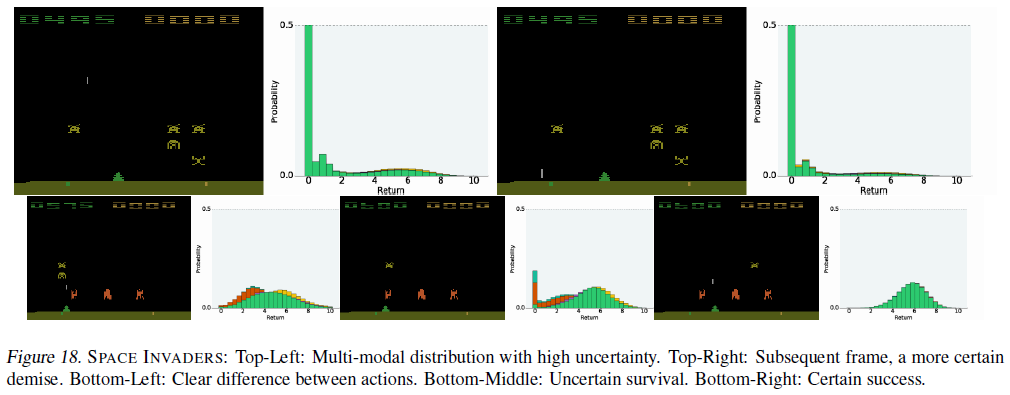
　　图4展示了我们在实验中观察到的典型价值分布。在此示例中，三个动作（包括按下按钮的动作）导致智能体过早释放其激光并最终导致游戏失败。相应的分布反映了这一点：它们为0（最终价值）分配了显著的概率。安全动作的分布类似（跟踪入侵者运动的LEFT稍占优势）。这个例子可以解释为什么我们的方法如此成功：分布更新将低价值的“失败”事件与高价值的“生存”事件分开，而不是将它们平均为一个（无法实现的）期望。³

　　一个令人惊讶的事实是，尽管ALE具有确定性，但分布并不集中于一个或两个价值，而是通常接近于高斯分布。我们认为这是由于我们离散化了由γ引起的扩散过程。

 

²对于N = 51, 我们的Tensorflow实现的训练速度是DQN的75%。
³视频: http://youtu.be/yFBwyPuO2Vg.

 

5.1. Varying the Number of Atoms

　　我们首先研究了算法在训练游戏中与原子数有关的性能（图3）。对于本实验，我们将ε设置为0.05。从数据中可以清楚地看出，使用太少的原子会导致不良的行为，并且更经常地会提高性能。这并不是立即显而易见的，因为我们可能期望饱和网络容量。51原子版本与DQN之间在性能上的差异特别引人注目：后者在所有五款游戏中均表现出色，在SEAQUEST中，我们获得了最先进的性能。作为比较的另一点，在5个游戏中有3个游戏，单参数Bernoulli算法的性能优于DQN，并且在ASTERIX中最显著。 

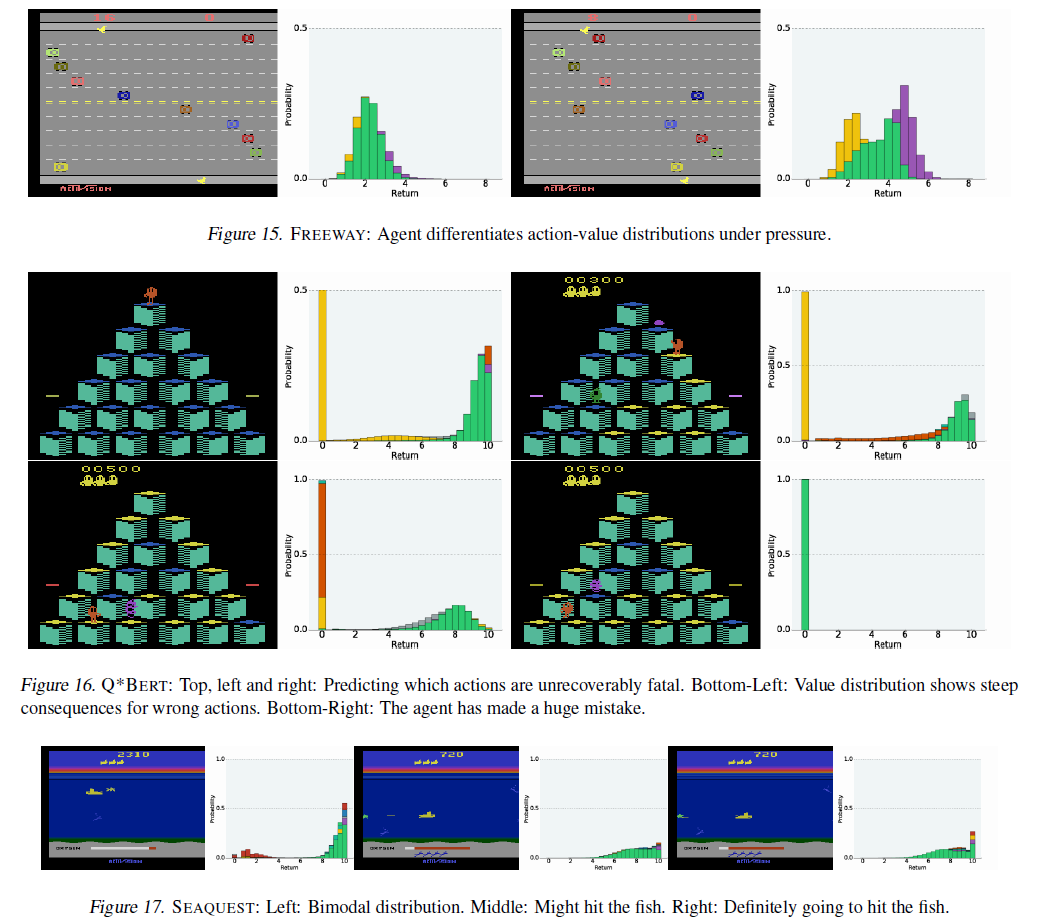
　　该实验的一个有趣结果是发现我们的方法确实提高了随机性。PONG具有内在的随机性：奖励的确切时机取决于内部寄存器，实际上是不可观察的。我们在智能体的预测中清楚地看到了这一点（图5）：在五个连续的帧中，价值分布显示了两种模式，表明智能体认为自己尚未获得奖励。有趣的是，由于智能体的状态不包括过去的奖励，因此在获得奖励后甚至无法消除预测，从而解释了模式的相对比例。

 

5.2. State-of-the-Art Results

　　上一节介绍的51原子智能体（从此处开始，C51）在训练游戏中的表现特别出色，因为它不涉及最新智能体中的其他算法思想。接下来，我们询问合并最常见的超参数选择（即较小的训练ε）是否可以带来更好的结果。具体来说，我们设置ε = 0.01（而不是0.05）；此外，每100万帧，我们以ε = 0.001评估智能体的性能。
　　我们将我们的算法与DQN（ε = 0.01），双重DQN（van Hasselt et al., 2016），对偶结构（Wang et al., 2016）和优先回放（Schaul et al., 2016）进行了比较， 比较训练期间取得的最优评估分数。我们看到C51明显优于其他算法（图6和7）。实际上，C51在许多游戏中（尤其是SEAQUEST）大大超越了当前的最新技术水平。一个特别引人注目的事实是该算法在稀疏奖励游戏（例如VENTURE和PRIVATE EYE）上的良好性能。这表明价值分布能够更好地传播很少发生的事件。完整的结果在附录中提供。
　　我们还在附录中（图12）包括了一个比较，该比较取3个种子的均值，显示出C51的训练性能胜过完全训练的DQN和人类玩家的比赛次数。这些结果继续显示出巨大的进步，并且更能代表智能体的平均性能。在五千万个帧中，C51在57场比赛中有45场的性能优于训练有素的DQN智能体。这表明，对于评估ALE中的强化学习算法而言，不需要完整的2亿个训练框架及其后续的计算成本。

　　最新版的ALE包含旨在防止轨迹过拟合的随机执行机制。具体而言，在每一帧上，环境都会以p = 0.25的概率拒绝智能体的选定动作。尽管DQN在随机执行方面大多数情况下都很健壮，但在某些游戏中DQN的性能有所下降。在针对随机和DQN智能体进行归一化的评分尺度上，C51得到的平均和中位数评分分别提高了126％和21.5％，这证实了C51在确定性设置之外的优势。

 

6. Discussion

　　在这项工作中，我们寻求了更完整的强化学习图片，其中涉及价值分布。我们发现学习价值分布是一个强大的概念，它使我们无需进行进一步的算法调整即可超越以前在Atari 2600上获得的最大收益。

 

6.1. Why does learning a distribution matter?

　　令人惊讶的是，当我们使用旨在最大化期望回报的策略时，我们应该看到性能方面的任何差异。我们希望做出的区别是，学习分布在存在近似的情况下很重要。现在，我们概述一些可能的原因。

 

Reduced chattering. 我们在第3.4节中的结果强调了Bellman最优算子的显著不稳定性。当与函数逼近结合使用时，这种不稳定性可能会阻止策略收敛，Gordon（1995）称之为chattering。我们认为，基于梯度的分类算法能够通过有效地平均不同的分布来减轻这些影响，类似于保守的策略迭代（Kakade＆Langford, 2002）。虽然chattering持续存在，但它已集成到近似解决方案中。

 

State aliasing. 即使在确定性环境中，状态混叠也可能导致有效的随机性。例如，McCallum（1995）指出了在部分可观察的领域中将表示学习与策略学习结合起来的重要性。我们看到了PONG中的状态混叠示例，其中智能体无法准确预测奖励时间。再次，通过显式建模结果分布，我们提供了更稳定的学习目标。

 

A richer set of predictions. 人工智能中反复出现的主题是从多种预测中学习智能体的想法（Caruana, 1997; Utgoff＆Stracuzzi, 2002; Sutton et al., 2011; Jaderberg et al., 2017）。分布方法自然为我们提供了丰富的辅助预测集，即：回报具有特定价值的概率。但是，与以前提出的方法不同，这些预测的准确性与智能体的性能紧密相关。

 

Framework for inductive bias. 强化学习的分布观点提供了一个更自然的框架，我们可以在该框架内对领域或学习问题本身进行假设。在这项工作中，我们使用支持被限制在[V_MIN, V_MAX]中的分布。将这种支持视为超参数，可以让我们通过将所有极值回报（例如大于V_MAX）视为等价物来更改优化问题。令人惊讶的是，DQN中类似的价值裁剪明显降低了大多数游戏的性能。再举一个例子：正如一些作者所论证的那样，将折扣因子解释为适当的概率会导致产生不同的算法。

 

Well-behaved optimization. 公认的是，分类分布之间的KL散度是一个很容易使损失最小化的损失。这可以解释我们的一些经验表现。然而，早期关于替代损失的实验（例如连续密度之间的KL散度）并未取得成果，部分原因是KL散度对其结果的价值不敏感。与我们在此给出的结果相比，更紧密地最小化Wasserstein度量应该会产生更好的结果。

　　最后，我们认为我们的结果强调了需要考虑算法设计中理论或其他方面的分布。

 

A. Related Work

　　据我们所知，最接近我们的工作是两篇论文（Morimura et al., 2010b;a），从累积分布函数的角度研究了分布Bellman方程。作者提出了参数和非参数解决方案，以学习风险敏感型强化学习的分布。他们还为策略评估设置提供了一些理论分析，包括非参数情况下的一致性结果。相比之下，我们还分析了控制设置，并强调了使用分布方程来改善近似强化学习。
　　在风险敏感的情况下，对回报的方差进行了广泛的研究。值得注意的是，Tamar et al.（2016）分析了使用线性函数逼近法来学习该方差以进行策略评估，而Prashanth＆Ghavamzadeh（2013）估计了风险敏感的执行者-评论者算法设计中的回报方差。Mannor＆Tsitsiklis（2011）提供了关于最优控制问题的方差约束解的计算的负面结果。
　　建模不确定性时也会出现分布方程。Dearden et al.（1998）考虑了对价值分布的高斯近似，并使用正态伽马先验模型对该近似的参数的不确定性进行建模。Engel eet al.（2005）利用分布Bellman方程来定义未知价值函数上的高斯过程。最近，Geist＆Pietquin（2010）提出了基于无迹Kalman滤波器的相同问题的替代解决方案。我们相信，我们在此处提供的许多分析方法都可以处理不确定性，这些分析涉及环境的固有随机性。

　　我们在这里的工作基于许多基础结果，尤其是关于替代最优标准。早些时候，Jaquette（1973）指出，可以实现一个矩最优准则，该准则将总体排序强加于分布，并定义了平稳的最优策略，与定理1的第二部分相呼应。通常将Sobel（1982）作为回报的较高矩（而不是分布）的Bellman方程的第一参考。Chung＆Sobel（1987）提供了有关总变化距离中分布Bellman算子收敛性的结果。White（1988）从优化状态对状态-动作对占用的角度研究了“非标准MDP标准”。
　　近年来，已经提出了许多用于强化学习的概率框架。作为推理的规划方法（Toussaint＆Storkey, 2006；Hoffman et al., 2009）将回报嵌入图形模型，并应用概率推理来确定导致最大期望奖励的动作顺序。Wang et al.（2008）考虑了强化学习的对偶表述，其中一个优化了平稳分布，它受转换函数给定的约束（Puterman, 1994），特别是它与线性逼近的关系。与此相关的是压缩和控制算法Veness et al.（2015），它通过使用密度模型学习回报分布来描述价值函数。这项工作的目的之一是解决他们的工作是否悬而未决的问题，即是否可以基于Bellman方程而不是Monte Carlo估计来设计一种实用的分布算法。

 

B. Proofs

 

C. Algorithmic Details

　　虽然我们的训练机制非常接近DQN（Mnih et al., 2015），但我们使用Adam（Kingma＆Ba, 2015）而不是RMSProp（Tieleman＆Hinton, 2012）进行梯度缩放。我们还为最终结果执行了一些超参数调整。具体来说，我们在五个训练游戏中评估了两个超参数，然后选择效果最佳的价值。我们考虑的超参数价值为V_MAX ∈ {3, 10, 100}，且ε_adam ∈ {1/L, 0.1/L, 0.01/L, 0.001/L, 0.0001/L}，其中L = 32是最小批大小。我们发现V_MAX = 10且adam = 0.01/L表现最佳。我们使用与DQN（α= 0.00025）相同的步长值。
　　算法1中给出了分类算法的伪代码。我们将Bellman更新分别应用于每个原子，然后将其投影到原始支持中的两个最接近的原子中。用γ_t = 0处理到终止状态的转换。

 

D. Comparison of Sampled Wasserstein Loss and Categorical Projection
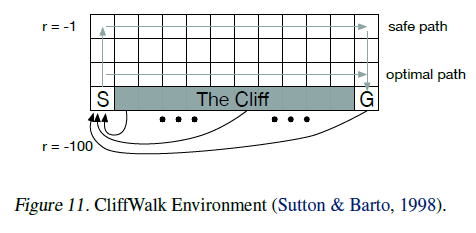
　　引理3证明，对于固定策略，分布Bellman算子在中是γ-压缩，因此T^π将在分布中收敛到回报Z^π的真实分布。在本节中，我们在图11所示的CliffWalk域上经验地验证这些结果。问题的动态与Sutton＆Barto（1998）给出的动态相匹配。我们还研究了样本Wasserstein损失和分类投影（等式7）下的分布Bellman算子的收敛性，采用试图采取安全路径但有10％的机会均匀随机采取动作的策略。

　　我们使用来自每个状态的10000个蒙特卡洛（MC）展开来计算回报Z^π的真实分布。然后，我们执行两个实验，分别用离散分布近似每个状态下的价值分布。
　　在第一个实验中，我们使用Wasserstein损失或具有交叉熵损失的分类投影（等式7）进行监督学习。 我们使用Z^π作为监督目标，并对所有状态执行5000次扫描，以确保两种方法都收敛。在第二个实验中，我们使用相同的损失函数，但训练目标来自具有采样转换的单步分布Bellman算子。我们使用V_MIN = -100，V_MAX = -1。⁴对于样本更新，我们对状态空间执行10倍的扫描次数。从根本上讲，这些实验研究了两种训练方式（最小化Wasserstein或类别损失）在理想（监督目标）和实际（采样的一步式Bellman目标）条件下将Wasserstein度量最小化的程度。

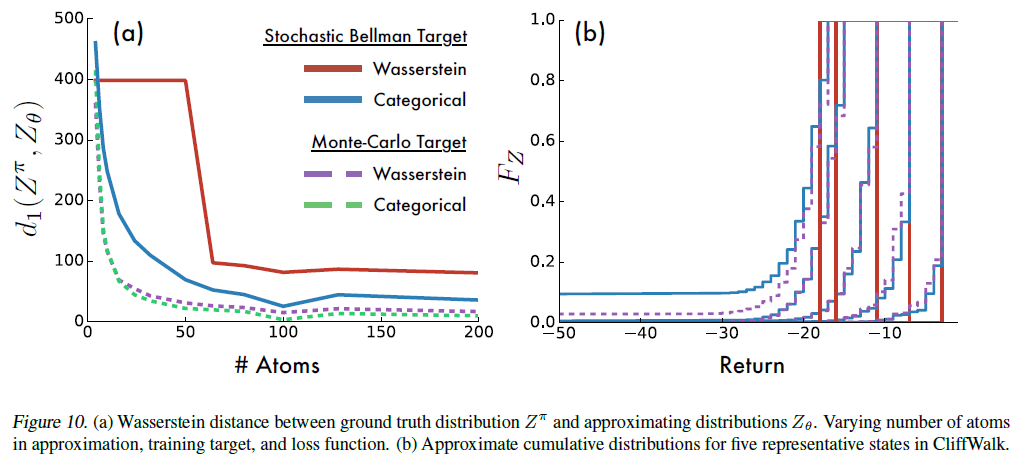
　　在图10a中，我们显示了随着我们改变原子数，在学习的分布和真实分布之间的最终Wasserstein距离d₁(Z^π, Z_θ)。该图显示，分类算法确实在监督和样本Bellman设置中确实最小化了Wasserstein度量。它还强调指出，用随机梯度下降来最小化Wasserstein损失通常是有缺陷的，这证实了命题5的直觉。在重复实验中，该过程收敛于d₁(Z^π, Z_θ)的不同值，表明存在局部最小值 （原子越少越普遍）。
　　图10提供了更多有关为何采样的Wasserstein距离性能可能较差的见解。在这里，我们看到了沿着CliffWalk的安全路径对五个不同状态在这两个损失下获得的近似价值的累积密度。Wasserstein已经收敛到一个不动点分布，但是没有一个能够很好地捕获真实的（蒙特卡洛）分布。相比之下，分类算法可以更准确地捕获真实分布的方差。

 

⁴由于存在较大的负回报的可能性很小，因此不可避免会有一些近似误差。但是，在我们的实验中，这种影响相对可以忽略不计。

 

E. Supplemental Videos and Results

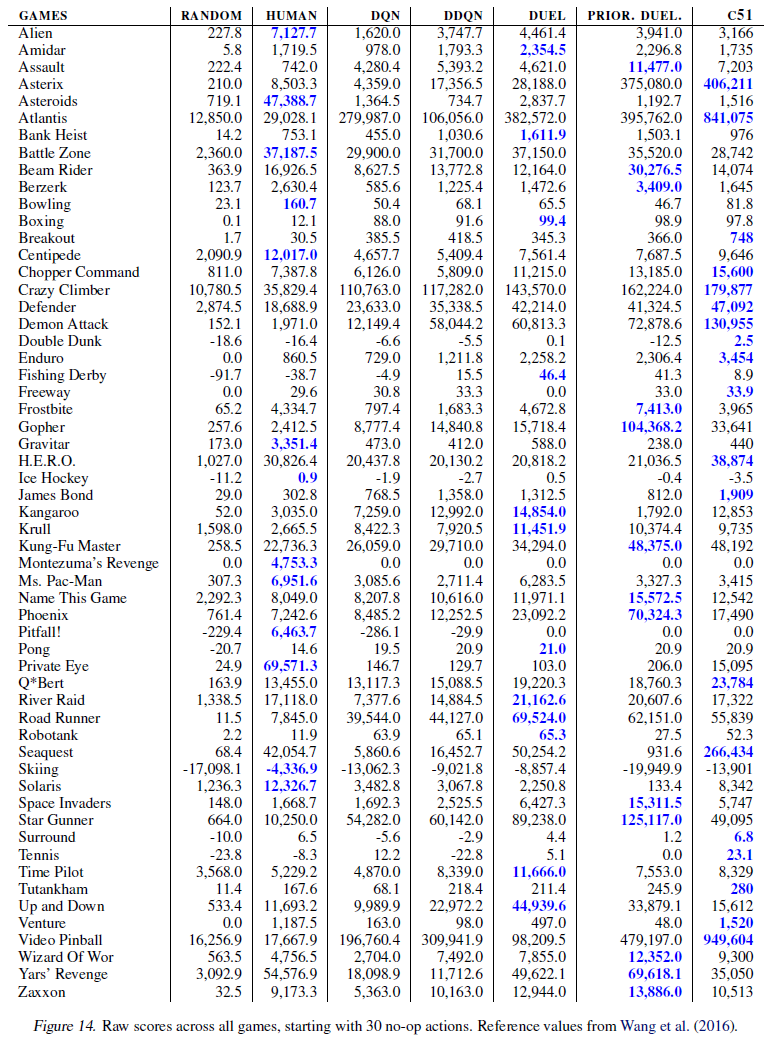
　　在图13中，我们提供了指向补充视频的链接，这些视频显示了在各种Atari 2600游戏中进行训练期间的C51智能体。图12显示了C51在训练过程中的相对性能。图14提供了一个评估结果表，将C51与其他先进智能体进行了比较。图15–18描绘了特别有趣的帧。