Inherent Adversarial Robustness of Deep Spiking Neural Networks: Effects of Discrete Input Encoding and Non-Linear Activations

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

 arXiv:2003.10399v2 [cs.CV] 23 Jul 2020

ECCV 2020

¹ https://github.com/ssharmin/spikingNN-adversarial-attack

 

Abstract

　　在最近对可信任的神经网络的探索中，我们提出了一个潜在的候选，即脉冲神经网络（SNN）之于对抗攻击的内在鲁棒性。在这项工作中，我们证明对CIFAR数据集上的深度VGG和ResNet结构，在基于梯度的攻击下，SNN的对抗精度比无脉冲对应网络高，尤其是在黑盒攻击场景中。我们将这种鲁棒性归因于SNN的两个基本特性，并分析其效果。首先，我们证明了Poisson编码器引入的输入离散化在减少时间步骤数的情况下提高了对抗鲁棒性。其次，我们量化了LIF神经元的泄漏率增加时对抗精度的量。我们的结果表明，用LIF神经元和较小的时间步骤训练的SNN比用IF神经元和较大的时间步骤训练的SNN具有更强的鲁棒性。此外，通过提出一种从SNN生成攻击的技术，我们克服了在时域中创建基于梯度的对抗输入的瓶颈¹。

 

Keywords: 脉冲神经网络，对抗攻击，LIF神经元，输入离散化

 

1 Introduction

　　对抗攻击是当今深度神经网络在任务关键型应用中取得成功的最大挑战之一[16, 10, 32]。对抗攻击的基本概念是有目的地调节对神经网络的输入，使其足够微妙，以保持人眼无法察觉，但却能够将网络愚弄成错误的决定。这种恶意行为首次在2013年分别在计算机视觉和恶意软件检测领域由Szegedy et al.[27]和Biggio et al.[4]证明 。从那时起，人们提出了许多防御机制来解决这个问题。一类防御包括精确调整网络参数，如对抗训练[11, 18]、网络蒸馏[22]、随机激活剪枝[8]等。另一类则侧重于在通过网络之前对输入进行预处理，如温度计编码[5]、输入量化[31, 21]，压缩[12]等。不幸的是，这些防御机制中的大多数已经被许多反击技术证明是无效的。例如，在[1]中提出的攻击下，基于“梯度掩模”的防御集合被攻破。防御蒸馏被Carlini-Wagner方法[6, 7]打破。对抗训练倾向于过拟合训练样本，并且仍然容易受到迁移攻击[28]。因此，对抗攻击的威胁继续存在。

　　在现有最先进的网络中缺乏对抗鲁棒性的情况下，我们认为需要一个对于对抗攻击具有固有敏感性的网络。在这项工作中，我们提出脉冲神经网络（SNN）作为一个潜在的候选者，由于其与无脉冲网络的两个根本区别：

1. SNN基于离散二值数据（0/1）工作，而其无脉冲对应的模拟神经网络（ANN）接收连续值模拟信号。由于SNN是一个基于二值脉冲的模型，输入离散化是网络的一个组成元素，最常用的是Poisson编码。
2. 与ANN中使用的分段线性ReLU激活相比，SNN使用生物学启发的IF或LIF神经元的非线性激活函数。

　　在SNN对抗攻击领域所做的少数工作中[19, 2]，大多数工作仅限于简单数据集（MNIST）或浅层网络。然而，这项工作扩展到了复杂数据集（CIFAR）和深度SNN，它们可以达到与最新ANN[24, 23]相当的精度。为了与无脉冲网络进行鲁棒性比较，我们分析了两种不同类型的脉冲网络：（1）转换SNN（由ANN-SNN转换[24]训练）和（2）反向传播SNN（由ANN-SNN转换的网络，进一步由替代梯度反向传播[23]进行增量训练）。我们发现转换SNN不能比ANN表现出更强的鲁棒性。尽管文献[25]中的作者给出了类似的分析，但我们通过实验解释了这种差异背后的原因，从而建立了SNN具有对抗鲁棒性的必要标准。此外，我们还提出了一种利用替代梯度法生成SNN-crafted攻击的技术。我们的贡献总结如下：

• 我们表明，在基于梯度的黑盒攻击场景下，SNN的对抗精度要高于ANN，在这种情况下，各自的干净精度彼此具有可比性。攻击是在经过CIFAR10和CIFAR100数据集训练的深度VGG和ResNet架构上进行的。对于白盒攻击，比较取决于对手的相对优势。
• SNN的鲁棒性增强归因于两个基本特征：通过Poisson编码的输入离散化和LIF（或IF）神经元的非线性激活。
  • 我们研究在不同的输入预量化水平下²，SNN中使用的时间步骤数（推断延迟）如何改变对抗精度。对于反向传播SNN（用较少的时间步骤数训练），随着时间步骤数的减少，离散化量和对抗鲁棒性增加。模拟输入的预量化带来了进一步的改进。然而，转换SNN似乎仅依赖于输入预量化，但对时间步骤数的变化保持不变。由于这些转换SNN在更大的时间步骤数下工作[24]，通过输入平均来最小化量化效果，因此具有观测不变性。

  • 我们表明，ANN中的分段线性激活（ReLU）线性地将对抗扰动传播到整个网络，而LIF（或IF）神经元则减少了每一层扰动的影响。此外，LIF神经元的泄漏因子还具有一个额外的旋钮来控制对抗扰动。我们进行了定量分析，以证明泄漏对SNN的对抗鲁棒性的影响。

　　总体而言，我们表明，采用LIF神经元的SNN，经过基于替代梯度的反向传播训练，并且以较少的时间步骤数进行操作的SNN，比用ANN-SNN转换训练的SNN（需要IF神经元和更多的时间步骤数）更为鲁棒。因此，训练技术在满足对抗鲁棒SNN的先决条件方面起着至关重要的作用。

• 由于LIF（或IF）神经元的不连续梯度，SNN中基于梯度的攻击生成并不容易。我们提出了一种基于近似替代梯度来生成攻击的方法。

 

2 Background

2.1 Adversarial Attack

　　给定一个属于 i 类的干净图像x和一个经过训练的神经网络M，对抗图像x_adv需要满足两个标准：

1. x_adv在视觉上“类似”于x，即|x−x_adv|=ε，其中ε是一个小数字。
2. x_adv被神经网络误分类，即M(x_adv)≠i。

　　距离度量|·|的选择取决于用于创建x_adv的方法，ε是一个超参数。在大多数方法中，l₂或l_∞范数被用来测量相似度，ε值被限制在，其中归一化像素强度x∈[0, 1]和原始x∈[0, 255]。

　　在这项工作中，我们使用以下两种方法构造对抗样本：

Fast Gradient Sign Method (FGSM) 这是[11]中介绍的构造对抗样本的最简单方法之一。对于给定的实例x，真实标签y_true和网络J(x, ytrue)的相应代价函数，该方法的目的是寻找一个扰动δ，使得受|δ|<ε约束的被扰动的输入J(x+δ, y_true)的代价函数最大化。在封闭形式下，攻击被表述为：

这里ε表示攻击的强度。

 

Projected Gradient Descent (PGD) 这种方法，在[17]中提出，产生了更强大的对手。PGD基本上是FGSM的k步变量，计算如下：

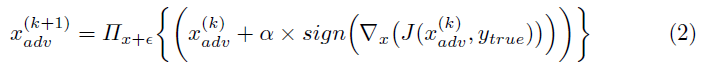
其中和α(≤ε)是指每次迭代或步骤使用的扰动量，k是迭代的总数。在x周围的ε-ball上执行其操作数的投影，即操作数被夹在x+ε和x-ε之间。此方法的另一个变体是在执行PGD操作之前，将强度ε的随机扰动添加到x。

 

2.2 Spiking Neural Network (SNN)

　　SNN和ANN之间的主要区是时间的概念。在ANN中，输入信号和中间节点输入/输出是静态模拟值，而在SNN中，它们是值为0或1的二值脉冲，也是时间函数。在输入层，采用Poisson事件生成过程将连续值模拟信号转换成二值脉冲序列。假设输入图像是一个像素强度在[0, 1]范围内的三维h×w×l矩阵。在SNN操作的每个时间步骤，为这些像素中的每一个生成随机数（根据正态分布N(0, 1)）（PS：原文写的是正态分布N(0, 1)，但理论上应该是均匀分布U(0, 1)）。如果对应的像素强度大于生成的随机数，则在该时间步骤触发脉冲。这个过程将持续T个时间步骤，为每个像素生成一个脉冲序列。因此，输入脉冲序列的大小为T×h×w×l。对于足够大的T，脉冲序列的时间平均值将与其模拟值成正比。SNN的每个节点都伴随着一个神经元。在众多的神经元模型中，最常用的是IF或LIF神经元。t+1时刻神经元膜电位的动态描述如下：

这里λ=1表示IF神经元，<1表示LIF神经元。w_i表示当前神经元与第 i 个前神经元之间的突触权重。x_i(t)是t时刻的第 i 个前神经元的输入脉冲。当V(t+1)达到阈值电压V_th时，产生输出脉冲，并且将膜电位复位到0，或者在软复位的情况下，（将膜电位）减少阈值电压的量。在输出层，根据过去总时间T后输出神经元的累积膜电位进行推断。

　　SNN的一个主要缺点是难以训练，特别是对于更深层的网络。由于SNN中的神经元具有不连续的梯度，标准梯度下降技术不直接适用。在这项工作中，我们使用了两种监督训练算法[24, 23]，即使对于深度神经网络和复杂的数据集，也能达到类似ANN的精度。

 

ANN-SNN Conversion 这种训练算法最初在[9]中概述，随后在[24]中针对深度网络进行了改进。注意，该算法只适用于训练含IF神经元的SNN。他们提出了一种阈值平衡技术，可以顺序地调整每一层的阈值电压。给定一个经过训练的ANN，第一步是在足够大的时间窗口内通过训练集生成网络的输入Poisson脉冲序列，以便其时间平均值准确地描述输入。接下来，在整个时间范围内记录由层1接收的（等式3中的项2）的最大值，用于多个小批量训练数据。这称为层1的最大激活。层1神经元的阈值被这个最大激活所代替，保持突触权重不变。这种阈值调整操作确保IF神经元的活动精确地模拟了相应ANN中的ReLU函数。在平衡层1阈值之后，该方法继续用于所有后续层。

 

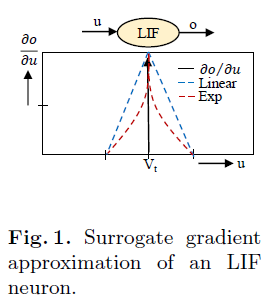
Conversion & Surrogate-Gradient Backpropagation 为了利用标准的基于反向传播的优化方法，[3, 33, 30]的作者引入了替代梯度技术。LIF（或IF）神经元的输入-输出特性是阶跃函数，其梯度在阈值处是不连续的（图1）。在替代梯度技术中，梯度是用类似线性或指数函数的伪导数来逼近的。文献[23]的作者利用导数中的脉冲时间信息，提出了一种新的梯度近似函数。时间步骤t处的梯度计算如下：

这里o^t是t时刻的输出脉冲，u^t是t时刻的膜电位，Δt是当前时间步骤和后神经元产生最后脉冲的时间步骤之间的差。α和β是超参数。一旦神经元的梯度被逼近，通过时间的反向传播（BPTT）[29]是用导数的链式规则来执行的。在BPTT中，网络在所有时间步骤上展开。最终输出被计算为每一时间步骤输出的累积，最后，损失被定义为总输出。在损失的反向传播过程中，梯度随时间累积并用于梯度下降优化。文献[23]的作者提出了一种混合训练方法，在替代梯度训练之前先进行ANN-SNN转换，以初始化网络的权重和阈值。与ANN-SNN转换相比，该方法有两个优点：一是既能训练IF神经元，又能训练LIF神经元的网络；二是训练所需的时间步骤数减少了10倍而不失精度。 

 

3 Experiments
3.1 Dataset and Models

　　我们对CIFAR10数据集上的VGG5与ResNet20和CIFAR100数据集上的VGG11进行了实验。VGG5的网络拓扑由conv3,64-avgpool-conv3,128(×2)-avgpool-fc1024(×2)-fc10组成。这里conv3,64是一个卷积层，有64个输出滤波器和3×3的核大小。fc1024是一个具有1024个输出神经元的全连接层。VGG11包含11个权重层，对应于[26]中的配置A，最大池化层被平均池化替换。ResNet20遵循[13]中为CIFAR10提出的结构，除了最初的7x7无残差卷积层被一系列两个3x3卷积层代替。对于ResNet20的ANN-SNN转换，仅对这些初始无残差单元执行阈值平衡（如[24]所示）。神经元（在ANN和SNN中）不含偏差项，因为它们在ANN-SNN转换期间对阈值电压的计算有间接影响。无偏差排除了批归一化（BN）[14]作为正则器使用的可能。取而代之的是，在每个ReLU之后使用一个dropout层（后面跟着一个池化层的除外）。

 

3.2 Training Procedure

　　我们的实验目的是比较3种网络的对抗攻击：1）ANN，2）通过ANN-SNN转换训练的SNN和3）带初始转换的反向传播训练的SNN。从这里开始，这些网络将分别称为ANN、SNN-conv和SNN-BP。

　　对于CIFAR10和CIFAR100数据集，我们遵循[17]中的数据增强技术：每边填充4个像素，从填充图像或其水平翻转中随机抽取32×32的区域进行裁剪。我们用原始32×32图像进行测试。使用前，训练和测试数据均归一化到[0, 1]。为了训练ANN，我们使用交叉熵损失和随机梯度下降优化（权重衰减=0.0001，动量=0.9）。VGG5（和ResNet20）共训练200个epoch，初始学习率为0.1（0.05），在第100（80）和150（120）个epoch学习率除以10。VGG11在CIFAR100上训练了250个具有相似学习规划的epoch。在训练SNN-conv网络期间，所有VGG和ResNet架构总共使用2500个时间步骤。利用交叉熵损失和adam[15]优化器（权重衰减=0.0005）对15个epoch的SNN-BP网络进行训练。初始学习率为0.0001，每5个epoch学习率减半。VGG5总共使用100个时间步骤，VGG11和ResNet20总共使用200个时间步骤。训练采用线性替代梯度近似[3]或脉冲时间相关近似[23]，其中α=0.3，β=0.01（等式4）。两种方法产生的结果大致相似。在所有情况下，泄漏因子λ均保持在0.99（泄漏影响分析除外）。

　　为了分析输入量化（不同时间步骤数）和泄漏因子的影响，仅使用CIFAR10数据集上的VGG5网络。

 

3.3 Adversarial Input Generation Methodology

　　为了白盒攻击的目的，我们分别为3个网络（ANN、SNN-conv、SNN-BP）构造对抗样本。ANN-crafted的FGSM和PGD攻击分别使用等式1和2中描述的标准技术生成。我们使用ε=8/255的非目标攻击。PGD攻击在迭代步骤k=7和每个步骤扰动α=2/255的情况下执行。FGSM或PGD方法由于其不连续的梯度问题而无法直接应用于SNN（在第2.2节中进行了描述）。为此，我们概述了基于替代梯度的FGSM（和PGD）技术。在SNN中，模拟输入X被转换成Poisson脉冲序列X_spike，该序列被送入第一个卷积层。如果X_rate是X_spike的时间平均值，则第一个卷积层X_conv1的膜电位可以近似为：

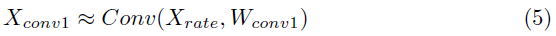
W_conv1是第一个卷积层的权重。从这个等式中，网络损失函数J关于X_rate或X的梯度符号用下式来描述（详细推导见附录）：

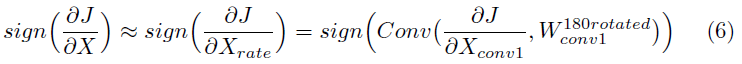
用替代梯度法从SNN中得到，这插入式6来计算关于输入的损失梯度符号。该符号矩阵随后用于根据标准FGSM或PGD方法计算X_adv。算法1总结如下：

 

4 Results
4.1 ANN vs SNN

　　表1总结了我们在白盒和黑盒设置中对CIFAR10（VGG5和ResNet20）和CIFAR100（VGG11）数据集的结果。对于每种架构，我们从三个网络开始：ANN，SNN-conv和SNN-BP，它们经过训练可达到相当的基准干净精度。让我们分别将它们称为M_ANN，M_SNN-conv和M_SNN-BP。在黑盒攻击期间，我们从经过单独训练的与目标模型网络拓扑相同但初始化不同的ANN中生成对抗测试数据集x_adv。显然，在FGSM和PGD黑盒攻击期间，SNN-BP的对抗精度高于相应的ANN和SNN-conv模型，而不管数据集或网络结构的大小如何（每种攻击案例的精度最高值用橙色文字突出显示）。下表列出了与ANN相比的Δ，即对抗精度的提高量。如果M_ANN和M_SNN-BP分别产生p_ANN％和p_SNN-BP％的对抗精度，则其Δ值等于p_SNN-BP％ - p_ANN％。另一方面，在白盒攻击期间，我们生成了三组对抗测试数据集：x_adv,ANN（从M_ANN生成），x_adv,SNN-conv（从M_SNN-conv生成）等。由于ANN和SNN具有广泛不同的操作动态和组成元素，因此在白盒攻击期间，所构造的对手的实力在ANN到SNN之间有显著变化（在第4.2节中演示）。SNN-BP显示CIFAR10数据集上的VGG和Resnet结构的白盒对抗精度都有显著提高（Δ范围从2％到4.6％）。相反，CIFAR100上的VGG11 ANN的白盒精度比SNN-BP高。我们将此差异归因于不同数据集和网络结构的ANN与SNN的对手强度差异。从表1中可以明显看出，在所有黑盒攻击案例（由一个常见对手攻击）中，SNN-BP网络在三个网络中展示出最高的对抗精度（橙色文字），而SNN-conv和ANN展示出可比的精度，与数据集，网络拓扑或攻击生成方法无关。因此，我们得出的结论是，当所有三个网络都受到相同的对抗输入攻击时，与它们的无脉冲对应模型以及SNN-conv模型相比，SNN-BP本质上具有更强的鲁棒性。重要的是，我们的结论仅针对VGG和ResNet架构和基于梯度的攻击而得到验证。

　　在接下来的两个小节中，我们将说明SNN的两个特性，这些特性有助于实现这种鲁棒性，以及SNN-conv无法显示类似行为的原因。

 

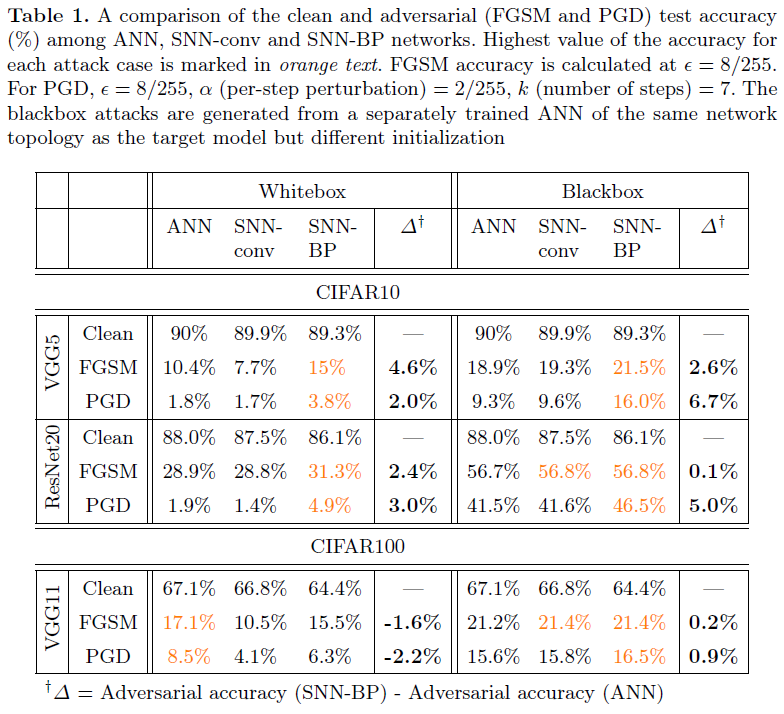
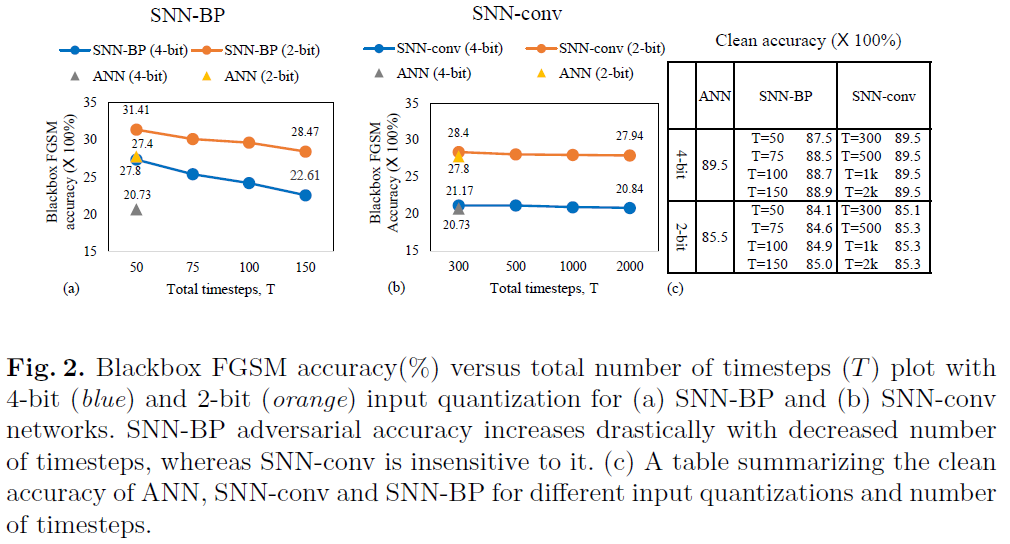
Effect of input quantization and number of timesteps 作为防御措施，非线性输入预处理的主要思想是离散化连续值输入信号，使网络对于对抗扰动变得不透明，只要它们位于离散化容器内。SNN是一种基于二值脉冲的网络，它要求将任何模拟值输入信号编码成二值脉冲序列，因此，我们相信它具有内在的鲁棒性。在我们的SNN模型中，我们采用Poisson rate编码，其中输出脉冲rate与输入像素强度成正比。但是，Poisson编码器引入的离散化量随使用的时间步骤数而变化。因此，只要干净精度保持在合理的范围内，就可以通过改变时间步骤数来控制网络的对抗损失。这种效果可以通过在输入Poisson编码器之前量化模拟输入进一步增强。在图2(a)中，我们用CIFAR10数据集演示了经过50、75、100和150个时间步骤训练的SNN-BP网络（VGG5）的FGSM对抗精度。当时间步骤数从150减少到50时，对于4-bit输入量化，精度提高了~5%（蓝线）。注意，如图2(c)中的表所示，在这个范围内，干净精度仅下降了1.4%，从88.9%（150个时间步骤）下降到87.5%（50个时间步骤）。时间步骤数的额外减少导致干净精度的更大降低。对应的ANN（4-bit输入量化）的对抗精度在同一图中用灰色三角形表示，以作比较。通过将模拟输入预量化为2-bits（橙线），得到了更高的对抗精度增加，并且与时间步骤数的趋势相同。因此，除了输入预量化之外，在SNN-BP中改变时间步骤数还引入了一个额外的旋钮来控制离散化的程度。相比之下，在图2(b)中，在SNN-conv网络上进行的类似实验表明，随着时间步骤数的增加，对抗精度几乎没有增加。只有对输入信号进行预量化才能使对抗精度从~21%提高至~28%。注意，用于SNN-conv（300到2000）的时间步骤数的范围远高于SNN-BP，因为转换后的网络具有更高的推理延迟。图3解释了SNN-conv对于时间步骤数的不变性的原因。我们绘制了4种情况下Poisson编码器的输入-输出特性：(b) 4-bit输入量化具有较小的时间步骤数（50和150），(c) 4-bit量化、较大的时间步骤数（300和2000）及其在(d)和(e)中的2-bit对应。从(c)和(e)可以明显看出，与量化相比，较大数量的时间步骤会产生更多的平均效应，因此，改变时间步骤的数量对转换图的影响可以忽略不计（实点线和虚线重合），而(b)和(d)则不如此。由于这种平均效应，SNN-conv的Poisson输出y趋向于遵循x_quant（量化ANN输入）的迹，导致在图2(b)中的整个时间步骤范围内与相应ANN的对抗损失相当。注意，在这些图中，输入x是指模拟输入信号，而输出y是脉冲序列的时间平均值（如图3(a)中的示意图所示）。

 

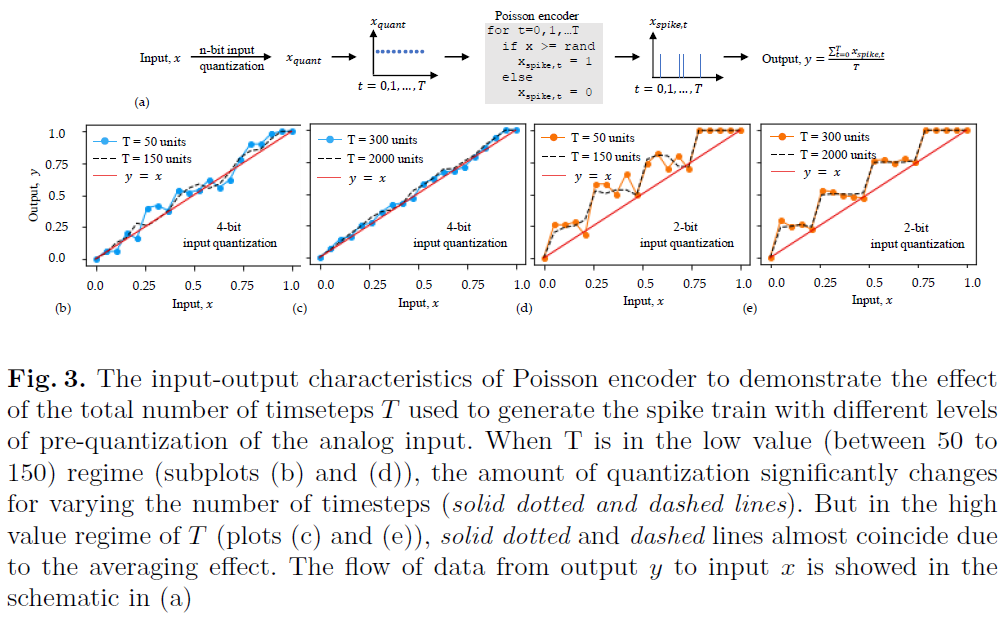
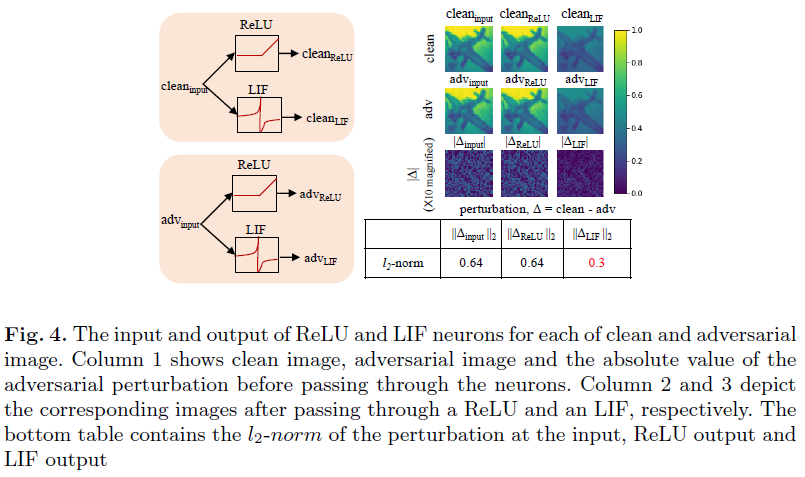
Effect of LIF (or IF) neurons and the leak factor SNN鲁棒性的另一个主要影响因素是其高度非线性的神经元激活（IF或LIF），而ANN主要使用像ReLU这样的分段线性激活。为了解释这种非线性的影响，我们进行了概念实验证明。我们给一个ReLU和一个LIF神经元（等式3中的λ=0.99）输入一个干净输入和相应的对抗输入。两个输入都是32×32图像，像素强度归一化为[0, 1]。图4中的第1、2和3行分别表示干净图像、对应的对抗图像及其绝对差异（扰动量）。注意，LIF神经元的输出在每个时间步骤都是二值的，因此，我们取整个时间窗口的平均值来获得相应的像素强度。ReLU无需任何转换即可通过干净输入和对抗输入，因此扰动的l2范数在输入和ReLU输出处相同（图中的底部表）。然而，LIF的非线性变换将输入层0.6的扰动降低到输出层的0.3。基本上，由于连续模拟值转换为二值脉冲表示，LIF（第3列）神经元的输出图像是输入图像的低像素版本。这种行为有助于减少通过网络传播的对抗干扰。IF神经元也表现出这种非线性转换。然而，由于它们在较长的时间窗口中的操作（如前一节所述），量化效果被最小化。与SNN-conv不同，SNN-BP网络可以用LIF神经元进行训练。LIF神经元中的泄漏因子提供了一个额外的旋钮来操纵这些网络的对抗鲁棒性。为了研究泄漏对鲁棒性的影响，我们建立了LIF神经元中泄漏因子与神经元脉冲rate的简单关系式。在这种情况下，根据V_t = λV_t-1 + V_input,t更新时间步骤t处的膜电位V_t。鉴于膜电位尚未达到阈值，因此，复位信号=0。这里，λ（<1）是泄漏因子，V_input,t是在时间步骤t时神经元的输入。让我们考虑这样一种场景，在每一时间步骤向神经元输入恒定电压V_mem，膜电位在n个时间步骤后达到阈值电压V_th。如图5所示，膜电位随时间呈几何级数变化。将替换为常数r后，我们得到脉冲rate（1/n）与泄漏因子（λ）之间的以下关系：

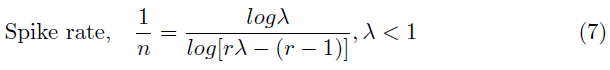
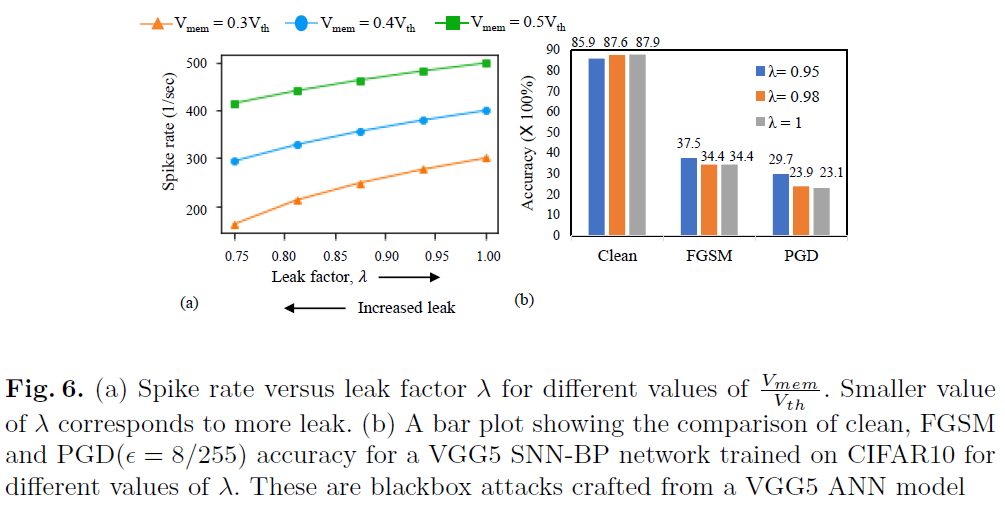
　　在图6(a)中，根据等式7，我们将脉冲rate绘制为不同V_mem值的泄漏因子λ的函数，其中λ在0.9999到0.75之间变化。在每种情况下，脉冲rate随着泄漏量的增加（较小的λ）而减小（即稀疏性，因此，鲁棒性增加）。图6(b)中的曲线证明了这一想法，在此我们展示了经过不同泄漏值训练的SNN-BP网络（CIFAR10上的VGG5）的对抗精度。对于FGSM和PGD攻击，当λ减小到0.95时，对抗精度增加了3~6%。请注意，具有不同泄漏因子的经过训练的SNN的清洁精度在~2％的范围内。除了稀疏性外，泄漏使得膜电位（反过来，输出脉冲rate）依赖于输入脉冲序列的时间信息[20]。因此，对于给定的输入，当IF神经元产生确定的脉冲模式时，LIF神经元的输入-输出脉冲映射是不确定的。这种效果随着泄漏的增加而增强。我们假设这一现象在一定程度上也与反向传播SNN的鲁棒性随着泄漏增加而增强有关。这里值得一提的是，当神经元的输入与泄漏因子保持不变时，等式7成立。在我们的实验中，我们从同一个初始化的ANN-SNN转换网络开始训练具有不同λ值的SNN-BP。因此，使用不同泄漏因子训练的SNN-BP参数彼此变化不大。因此，等式中的假设适用于我们的结果。

 

4.2 ANN-Crafted vs SNN-Crafted Attack

　　最后，我们提出了一种借助于替代梯度计算的SNN的attack-crafting技术。方法的细节在第3.3节中进行了解释。表2总结了ANN-crafted和SNN-crafted（我们提出的技术）攻击之间的对比。注意，这些都是黑盒攻击，即我们为3个网络（ANN、SNN-conv、SNN-BP）分别训练两个独立初始化的模型。其中一个用作源（标记为ANN-I、SNN-conv-I等），另一个用作黑箱场景中的目标（标记为ANN-II、SNN-conv-II等）。很明显，SNN-BP的对抗精度（最后一行）对于SNN-crafted和ANN-crafted的输入都是最高的。此外，让我们分析表2第1行中的FGSM攻击。当ANN-II被ANN-I攻击时，FGSM精度为18.9%，而如果被SNN-conv-I（或SNN-BP-I）攻击，精度为32.7%（或31.3%）。因此，这些结果表明，ANN-crafted攻击比相应的SNN对应体强。

 

5 Conclusions

　　ANN中当前的防御机制无法防止一系列对抗攻击。在这项工作中，我们表明，由于输入编码的离散性和LIF（或IF）神经元的非线性激活函数，因此SNN具有固有的抵御基于梯度的对抗攻击的能力。通过减少输入脉冲生成过程中的时间步骤数并增加LIF神经元的泄漏量，可以进一步提高弹性。与使用基于脉冲的反向传播（使用LIF神经元）训练的相应SNN相比，使用ANN-SNN转换技术（使用IF神经元）训练的SNN需要更多的时间步骤进行推断。因此，前一种技术产生更鲁棒的SNN。我们的结论仅针对具有CIFAR数据集的深VGG和ResNet网络上基于梯度的攻击得到了验证。将来需要对各种攻击方法和结构进行分析。我们还提出了一种通过使用替代梯度从SNN生成基于梯度的攻击的方法。