Communication-Efficient Learning of Deep Networks from Decentralized Data
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS) 2017, Fort Lauderdale, Florida, USA. JMLR: W&CP volume 54. Copyright 2017 by the author(s).
Abstract
现代移动设备可以访问大量适合模型学习的数据,从而大大改善设备上的用户体验。例如,语言模型可以改善语音识别和文本输入,图像模型可以自动选择好的照片。然而,这些丰富的数据往往对隐私敏感,数量庞大,或者两者兼而有之,这可能会妨碍登录到数据中心并使用传统方法进行训练。我们提倡一种替代方法,将训练数据分布在移动设备上,并通过聚集本地计算的更新来学习共享模型。我们将这种去中心化的方法称为联邦学习。我们提出了一种基于迭代模型平均的深度网络联邦学习的实用方法,并对五种不同的模型结构和四种数据集进行了广泛的实证评估。这些实验表明,该方法对不平衡和非独立同分布(non-IID)的数据分布具有鲁棒性,这是该设置的一个定义特征。通信成本是主要的限制条件,与同步随机梯度下降相比,我们所需的通信轮数减少了10–100倍。
1 Introduction
手机和平板电脑日益成为许多人的主要计算设备[30,2]。这些设备(包括摄像头、麦克风和GPS)上强大的传感器,再加上它们经常被携带,意味着它们能够获得前所未有的数据量,其中大部分数据是私有的。在这些数据上学习到的模型有希望通过驱动更智能的应用程序来大大提高可用性,但数据的敏感性意味着将其集中存储存在风险和责任。
我们研究了一种学习技术,它允许用户在不需要集中存储数据的情况下,从这些丰富的数据中获得共享模型的好处。因为学习任务是通过一个由中央服务器协调的参与设备(我们称之为客户机)的松散联合来解决的,所以我们称之为联邦学习。每个客户机都有一个从未上载到服务器的本地训练数据集。相反,每个客户机对由服务器维护的当前全局模型进行更新计算,并且只传递此更新到服务器。这是对《2012年白宫消费者数据隐私报告》提出的集中收集或数据最小化原则的直接应用[39]。由于这些更新是专门用于改进当前模型的,因此没有理由在应用后进行存储。
这种方法的一个主要优点是将模型训练与直接访问原始训练数据的需求分离开来。显然,负责协调训练的服务器仍然需要一些信任。但是,对于可以根据每个客户端上可用的数据指定训练目标的应用程序,联邦学习可以通过将攻击面仅限于设备,而不是设备和云,来显著降低隐私和安全风险。
我们的主要贡献是:1)将移动设备分散数据训练问题,作为一个重要的研究方向;2)选择出了一种可应用于此设置的简单实用的算法;3)对提出的方法进行了广泛的实证评估。更具体地说,我们引入了联邦平均(FederatedAveraging)算法,它将每个客户机上的局部随机梯度下降(SGD)与执行模型平均的服务器相结合。我们对该算法进行了大量的实验,证明了该算法对不平衡和非IID数据分布的鲁棒性,并能将在分散数据上训练深度网络所需的通信次数减少若干个数量级。
Federated Learning 联邦学习的理想问题具有以下特性:1)对来自移动设备的真实数据进行训练比对数据中心中通常提供的代理数据进行训练具有明显的优势。2)此数据对隐私敏感或大小较大(与模型的大小相比),因此最好不要仅出于模型训练(服务于集中收集原则)的目的将其记录到数据中心。3)对于有监督的任务,数据上的标签可以从用户交互中自然推断出来。
许多支持移动设备智能行为的模型都符合上述标准。作为两个例子,我们考虑了图像分类,例如预测哪些照片在未来最可能被多次查看或共享;以及语言模型,通过改进解码、预测下一个单词,甚至预测整个回复[10]来改进触摸屏键盘上的语音识别和文本输入。这两项任务的潜在训练数据(用户拍摄的所有照片以及他们在移动键盘上键入的所有内容,包括密码、URLs、消息等)可能对隐私敏感。这些示例的分布也可能与容易获得的代理数据集有很大的不同:在聊天和文本消息中使用的语言通常与标准语言语料库(如维基百科和其他Web文档)有很大的不同;人们拍摄在他们手机上的的照片可能与典型的Flickr照片大不相同。最后,这些问题的标签是直接可用的;输入的文本是用于语言模型学习的自我标签,照片标签可以通过用户与他们的照片应用程序的自然交互来定义(哪些照片是删除、共享或查看的)。
这两项任务都非常适合神经网络学习。对于图像分类任务,前馈深度网络,尤其是在特定的卷积网络,能够提供最先进的结果[26,25]。对于语言建模任务,递归神经网络,尤其是LSTMs,已经取得了最先进的结果[20,5,22]。
Privacy 与数据中心对持久数据的训练相比,联邦学习具有明显的隐私优势。即使拥有一个“匿名”的数据集,通过与其他数据的连接,仍然会使用户隐私受到威胁[37]。相比之下,联邦学习传输的信息是改进特定模型所必需的最小更新(自然地,隐私获益的强度取决于更新的内容)。更新本身可以(并且应该)是短暂的。它们永远不会包含比原始训练数据更多的信息(由于数据处理的不平等),而且通常包含的信息要少得多。此外,聚合算法不需要更新的来源,因此可以在不识别元数据的情况下通过混合网络(如Tor[7])或受信任的第三方传输更新。本文最后简要讨论了联邦学习与安全多方计算和差异隐私相结合的可能性。
Federated Optimization 我们将联邦学习中隐含的优化问题称为联邦优化,并与分布式优化建立了联系(和对比)。联合优化有几个关键特性,可以将其与典型的分布式优化问题区分开来:
- 非独立同分布:给定客户机上的训练数据通常基于特定用户对移动设备的使用,因此任何特定用户的本地数据集都不能代表总体分布。
- 不平衡:同样,一些用户会比其他用户更频繁地使用服务或应用程序,从而导致不同数量的本地训练数据。
- 大规模分布:我们预计参与优化的客户机数量将远远大于每个客户机的平均样例数量。
- 有限的沟通:移动设备经常处于离线状态,或连接速度慢或费用高。
在这项工作中,我们的重点是优化的非IID和不平衡特性,以及通信约束的临界性质。部署的联邦优化系统还必须解决大量的实际问题:随着数据的添加和删除而变化的客户端数据集;以复杂方式与本地数据分布相关联的客户端可用性(例如,来自美式英语使用者的电话与说英式英语使用者的电话充电有着不同的时间);以及客户从不响应或发送损坏的更新。
这些问题超出了当前工作的范围;相反,我们使用一个适合实验的受控环境,但仍然需要解决客户机可用性和不平衡和非IID数据的关键问题。我们假设一个同步更新方案,该方案进行多轮通信。有一组固定的K个客户机,每个客户机都有一个固定的本地数据集。在每一轮开始时,客户机随机划分成了占比为C的若干个部分,服务器将当前全局算法状态发送给每个客户机(例如,当前模型参数)。为了提高效率,我们只选择了一个部分的客户,因为我们的实验表明,超过某一点增加更多客户的回报会减少。然后,每个选定的客户机根据全局状态及其本地数据集执行本地计算,并向服务器发送更新。然后,服务器将这些更新应用于其全局状态,并重复该过程。
当我们关注非凸神经网络目标时,我们考虑的算法适用于任何形式的有限和目标
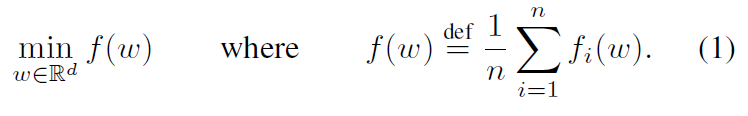
对于机器学习问题,我们通常采用 fi(w) = l(xi , yi ; w),即模型参数w在样例(xi;yi)上的预测损失。我们假设有K个客户机对数据进行划分,Pk是客户机k上的数据点的索引集,其中nk=|Pk|。因此,我们可以将目标(1)改写为
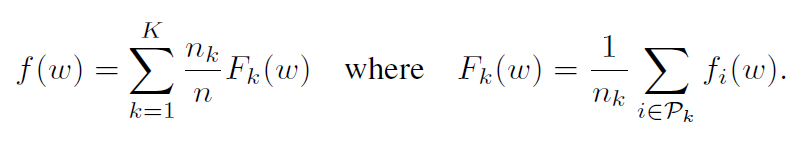
如果划分Pk是通过在客户机上均匀随机分布训练样例形成的,那么我们将得到 EPk[Fk(w)] = f(w),其中期望值计算的是分配给固定客户机k的一组样例。这是通常由分布式优化算法所做的IID假设;我们将其他情况称为非IID设置(即Fk可能是 f 的任意错误近似值)。
在数据中心优化中,通信成本相对较小,计算成本占主导地位,最近的许多重点是使用GPU来降低这些成本。相反,在联邦优化中,通信成本占主导地位——我们通常会受到1 MB/s或更低的上传带宽的限制。此外,客户通常只在接入电源和使用未计量的Wi-Fi连接时自愿参与优化。此外,我们希望每个客户每天只参与少量的更新轮次。另一方面,由于与总数据集大小相比,任何单个设备上的数据集都很小,而且现代智能手机具有相对较快的处理器(包括GPU),因此对许多类型的模型来说,与通信成本相比,计算基本上是免费的。因此,我们的目标是使用额外的计算来减少训练模型所需的通信轮数。有两种主要的方法可以添加计算:1)增加并行性,在每轮通信之间使用更多独立工作的客户机;2)增加每个客户机上的计算,而不是执行像梯度计算这样的简单计算,每个客户机在每轮通信之间形成一个更复杂的计算。我们研究了这两种方法,但是我们实现的加速主要是由于一旦使用了客户机上的最小并行级别,就在每个客户机上增加了更多的计算。
Related Work 局部迭代平均训练模型的分布式训练被McDonald等人[28]用于感知器,同时也被Povey等人[31]用于语音识别DNNs。Zhang等人[42]研究了具有“软”平均的异步方法。这些工作只考虑集群/数据中心的设置(最多16个工作人员,基于快速网络的挂钟时间),而没考虑不平衡和非IID的数据集。这是对联邦学习设置至关重要的属性。我们将这种类型的算法应用到联邦设置,并执行适当的实证评估。这体现出了不同于数据中心设置的问题,并且需要不同的方法。
与我们的动机相似,Neverova等人[29]也讨论了在设备上保留敏感用户数据的优点。Shokri和Shmatikov[35]的工作与我们有几个方面的关联:专注于训练深度网络,强调隐私的重要性,并且通过在每轮通信中只共享参数的一个子集来解决通信成本;但是,他们也没考虑不平衡的非IID数据,实证评估有限。
在凸设置中,分布式优化和估计问题受到了广泛关注[4,15,33],一些算法特别关注通信效率[45,34,40,27,43]。除了假设凸性之外,现有的工作通常要求客户机的数量比每个客户机的样例数量小得多,数据以IID的方式分布在客户机上,并且每个节点都有相同数量的数据点——所有这些假设都违反了联邦优化的设置。异步分布形式的SGD也被应用于训练神经网络,例如Dean等人[12]。但是这些方法需要在联邦设置中进行大量的更新。分布式共识算法(如[41])放宽了IID的假设,但仍然不适合在许多客户机上进行通信受限的优化。
我们考虑的(参数化)算法系列的一个端点是简单的单次平均,其中每个客户机都会解决模型问题,使本地数据损失最小化(可能是规则化),这些模型被平均以生成最终的全局模型。这种方法在具有IID数据的凸情况下得到了广泛的研究,并且众所周知,在最坏的情况下,生成的全局模型并不比在单个客户机上训练模型更好[44,3,46]。
2 The FederatedAveraging Algorithm
最近许多成功的深度学习应用几乎完全依赖于变量的随机梯度下降(SGD)来进行优化;事实上,许多进展可以理解为使模型结构(以及损失函数)更易于通过简单的基于梯度的方法[16]进行优化。因此,我们很自然地从SGD开始构建联邦优化算法。
SGD可以简单地应用于联邦优化问题,在联邦优化问题中,每轮通信都要进行一次单批梯度计算(比如在随机选择的客户机上)。这种方法计算效率很高,但需要大量的训练来生成好的模型(例如,即使使用先进的方法,如批量标准化,Ioffe和Szegedy[21]在MNIST数据集上用大小为60的小批量上训练了50000步)。我们在CIFAR-10实验中考虑了这个基线。
在联邦设置中,涉及更多客户时,壁钟时间成本很低。因此对于我们的基线,我们使用大批量同步SGD;Chen等人[8]的实验显示此方法在数据中心设置中是最先进的,它优于异步方法。为了在联邦设置中应用这种方法,我们在每一轮中选择占比为C的客户机,并计算这些客户机所持有的所有数据的损失梯度。因此,C控制全局批大小,C=1对应于整批(非随机)梯度下降。我们将此基线算法称为联邦SGD(或FedSGD)。

(部分省略) 也就是说,每个客户端使用其本地数据在当前模型上进行一步梯度下降,然后服务器对生成的模型进行加权平均。我们称之为联邦平均算法(FedAvg)。以这种方式编写算法后,我们可以在平均步骤之前多次迭代本地更新,从而向每个客户机添加更多的计算。计算量由三个关键参数控制:C,每轮执行计算的客户端的占比;E,每个客户端在每轮对本地数据集进行训练的次数;B,用于客户端更新的本地小批量大小。我们令B = ∞来表明将完整的本地数据集视为单个小批处理。因此,在该算法家族中,我们可以取B = ∞且E = 1,这与FedSGD完全对应。对于具有nk个本地样例的客户机,每轮本地更新的次数由uk = E * nk / B给出;完整的伪代码在算法1中给出。
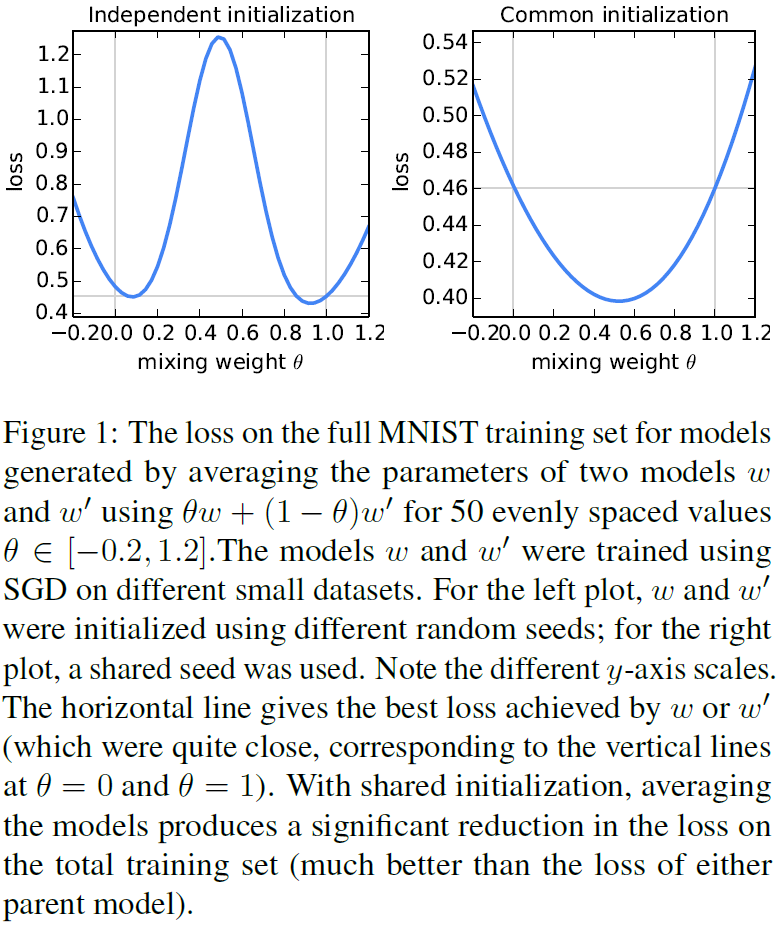
对于一般的非凸目标,参数空间中的平均模型会产生任意的坏模型。遵循Goodfellow等人[17]的方法,当我们将两个从不同初始条件训练的MNIST数字识别模型取平均时,我们可以看到这种不良表现(图1,左图)。对于这个图,父模型w和w’分别接受了来自MNIST训练集的600个不重叠的IID样本的训练。通过SGD进行训练,固定学习率为0.1,在大小为50的小批量上更新迭代了240次(或E=20,通过大小为600的小数据集)。这大约是模型开始过度适合其本地数据集的训练量。
最近的研究表明,在实践中,充分超参数化NNs的损失面表现出令人惊讶的良好,特别是比先前想象的更不容易出现不良的局部极小值[11,17,9]。事实上,当我们从相同的随机初始化开始两个模型,然后在不同的数据子集上对每个模型进行独立的训练(如上所述),我们发现简单的参数平均非常有效(图1,右):这两个模型的平均值,w/2+w'/2,实现了对整个MNIST训练集损失的大幅降低,而不是通过单独对任何一个小数据集进行训练而获得的最佳模型。虽然图1从随机初始化开始,但是注意到对于每一轮FedAvg都使用一个共享的启动模型wt,因此同样的直觉也适用。

3 Experimental Results
我们受到图像分类和语言建模任务的激励,良好的模型可以大大提高移动设备的可用性。对于这些任务中的每一个,我们首先选择一个足够小的代理数据集,这样我们就可以彻底研究FedAvg算法的超参数。虽然每个单独的训练运行相对较小,但我们为这些实验训练了2000多个单独的模型。然后,我们在基准CIFAR-10图像分类任务上给出了结果。最后,为了证明FedAvg在采用客户机自然划分数据的实际问题上的有效性,我们对一个大型语言建模任务进行了评估。
我们的初步研究包括两个数据集上的三个模型族。前两个用于MNIST数字识别任务[26]:1)一个简单的多层感知器,具有两个隐层,每个层有200个单元,使用ReLu激活(共199210个参数),我们称之为MNIST 2NN。2)具有两个5x5卷积层的CNN(第一个具有32个通道,第二个具有64个通道,每个通道后面都有2x2最大池),一个具有512个单元和ReLu激活的全连接层,以及一个最终的softmax输出层(总参数1663370)。为了研究联邦优化,我们还需要指定数据如何分布在客户机上。我们研究了在客户机上对MNIST数据进行划分的两种方法:IID,在IID中对数据进行洗牌,然后将数据分为100个客户机,每个客户机接收600个样例;而非IID,我们首先按数字标签对数据进行排序,将其分为200个大小为300的碎片,然后将这些碎片分配给100个客户机,每个客户机2个碎片。这是一个病理性的非IID数据分区,因为大多数客户只有两位数的样例。因此,这让我们可以探索我们的算法在高度非IID数据上的突破程度。然而,这两个划分都是平衡的。
为了进行语言建模,我们从威廉·莎士比亚的完整作品中构建了一个数据集[32]。我们用至少两行文本为剧本中每个有对话的角色构建了一个客户端数据集。这产生了一个拥有1146个客户机的数据集。对于每个客户机,我们将数据分成一组训练行(角色的前80%行)和测试行(最后20%,四舍五入到至少一行)。生成的数据集在训练集中有3564579个字符,在测试集中有870014个字符。这些数据基本上是不平衡的,许多角色只有几行,而少数角色有大量行。此外,观察测试集不是随机的线条样本,而是由每个剧本的时间顺序暂时分开的。使用相同的训练/测试拆分,我们还可以形成平衡和IID版本的数据集,同时拥有1146个客户机。
在这些数据上,我们训练了一个堆叠的字符级LSTM语言模型[22],该模型在读取一行中的每个字符后,预测下一个字符。该模型以一系列字符作为输入,并将每个字符嵌入到一个已知的8维空间中。然后通过两个LSTM层处理嵌入的字符,每个层有256个节点。最后,将第二个LSTM层的输出发送到softmax输出层,每个字符一个节点。整个模型有866578个参数,我们使用80个字符的展开长度进行训练。
SGD对学习速率参数η的调整很敏感。这里报告的结果是基于一个足够宽的学习率网格上的训练(通常给η取11-13个值,在一个乘法分辨率101/3或101/6网格上)。我们检查以确保最佳学习率在网格中间,并且最佳学习率之间没有显著差异。除非另有说明,我们为每个x轴值分别选择的最佳执行率绘制度量。我们发现,最佳学习率与其他参数之间的关联不大,不存在明显的函数关系。

Increasing parallelism 我们首先对客户端占比C进行实验,它控制多客户端并行的数量。表1显示了不同的C对两个MNIST模型的影响。我们报告了实现目标测试集精度所需的通信轮数。为了计算这一点,我们为每个参数设置组合构建了一条学习曲线,如前所述对η进行优化,然后利用在所有先前轮次中获得的测试集精度的最佳值,对每条曲线加以改进。然后,我们使用组成曲线的离散点之间的线性插值,计算曲线与目标精度交汇处的轮数。参考图2可以更好地理解这一点,其中灰色线表示目标。
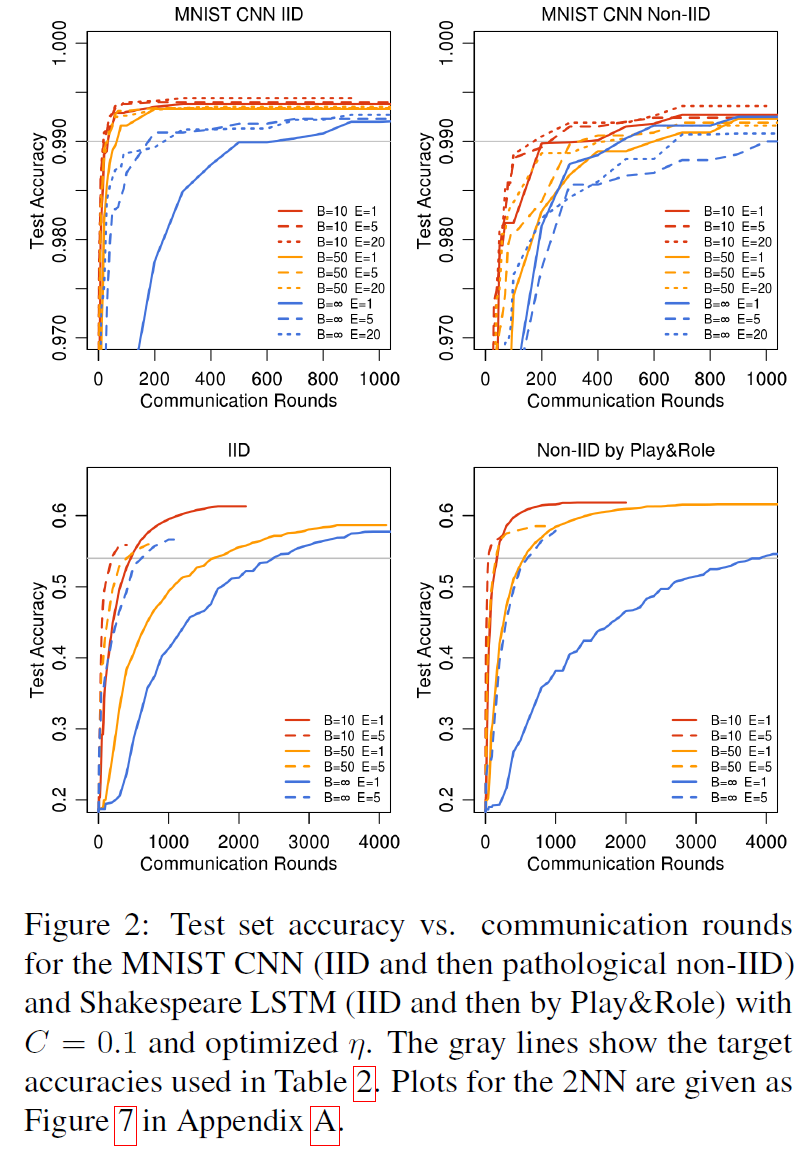
当B=∞时(对于MNIST,将所有600个客户机样例处理作为每轮的一批),增加客户机占比的优势很小。当使用C≥0.1时,特别是在非IID情况下,更小的批处理大小B=10显示出显著的改进。基于这些结果,在我们剩下的大部分实验中,我们将C=0.1固定下来,这在计算效率和收敛速度之间达到了很好的平衡。将表1中B=∞和B=10列的轮数进行比较,可以看到一个急剧性的加速,我们接下来将对此进行研究。
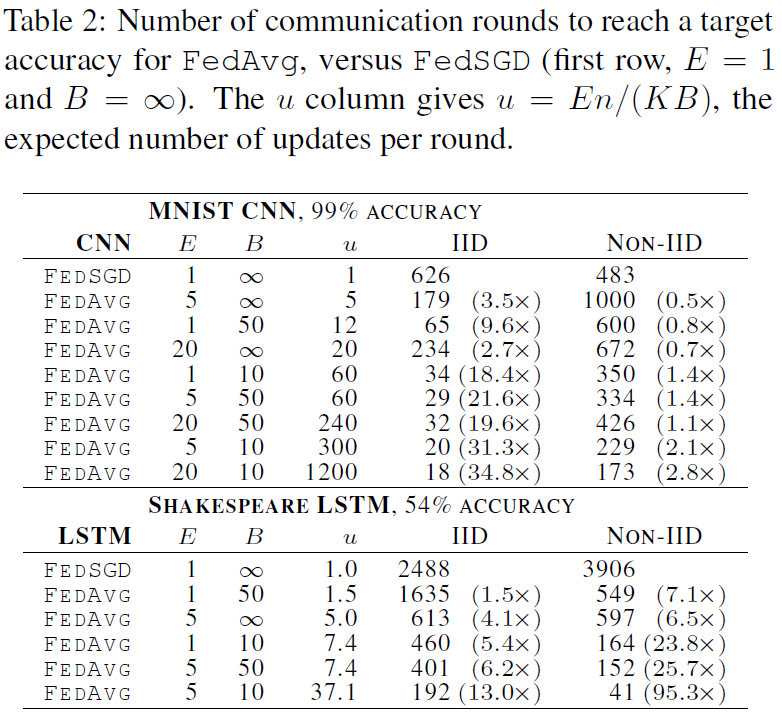
Increasing computation per client 在本节中,我们将C=0.1固定下来,并在每一轮中为每个客户机添加更多的计算,要么减少B,要么增加E,要么两者兼而有之。图2表明,每轮增加更多的本地SGD更新可以显著降低通信成本,表2量化了这些加速。每轮每个客户机的预期更新数为u = (E[nk] / B)E = nE / (KB) ,其中预期值超过随机客户机k的绘制值。我们通过此统计对表2的每个部分中的行进行排序。我们看到通过改变E和B来增加u是有效的。只要B足够大,可以充分利用客户机硬件上可用的并行性,就基本上不需要花费计算时间来降低它,因此在实践中,这应该是第一个被调优的参数。
对于MNIST数据的IID划分,每个客户使用更多的计算,减少了达到目标精度的轮数,其中CNN减少了35倍,2NN减少了46倍(有关2NN的详细信息,请参见附录A中的表4)。病理性划分非IID数据的加速率更小,但仍相当可观(2.8–3.7倍)。令人印象深刻的是,对训练不同数字对的模型参数,当我们幼稚地进行平均时,平均值提供了所有的优势(而实际上是分散的)。因此,我们认为这是该方法鲁棒性的有力证据。
莎士比亚(根据戏剧中的角色)的不平衡和非IID分布更能代表我们对现实应用所期望的那种数据分布。令人欣慰的是,对于这个问题,学习非IID和不平衡数据实际上要容易得多(95倍加速,而平衡IID数据为13倍加速);我们推测这主要是由于某些角色具有相对较大的本地数据集,这使得增加的本地训练尤其有价值。
对于所有的三个模型类,FedAvg比基线FedSGD模型收敛到更高的测试集精度水平。即使这些线超出了绘制的范围,这种趋势也会继续。例如,对于CNN来说,B=∞;E=1 FedSGD模型在1200轮之后最终达到99.22%的精度(6000轮之后没有进一步提高),而B=10;E=20 FedAvg模型在300轮之后达到99.44%的精度。我们推测,除了降低通信成本外,模型平均还能产生类似于Dropout[36]所获得的正则化收益。
我们主要关注的是泛化性能,但是FedAvg在优化训练损失方面也很有效,甚至超过了测试集精度的最大值。我们观察了所有三个模型类的类似行为,并在附录A的图6中展示了MNIST CNN的图。
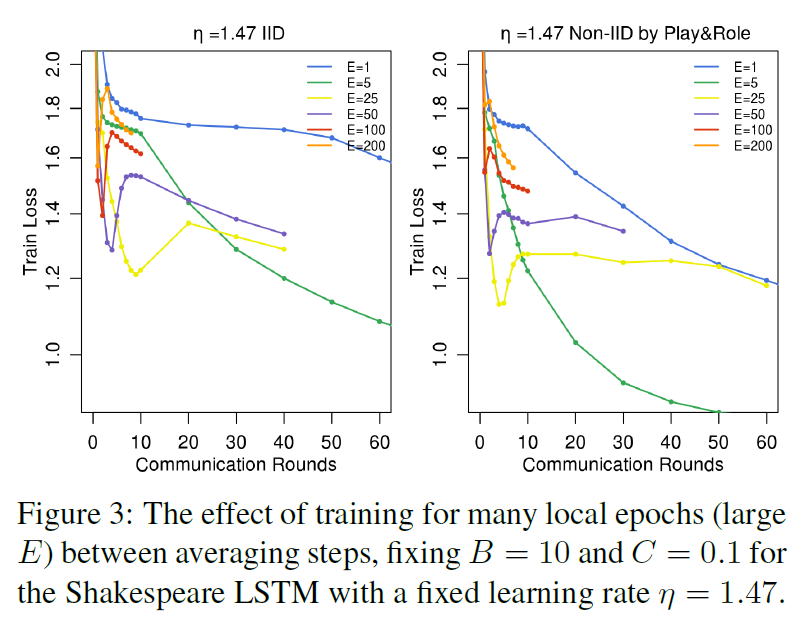
Can we over-optimize on the client datasets? 当前模型参数只影响通过初始化在每个ClientUpdate中执行的优化。因此,当E 一> ∞,至少对于凸问题,最终初始条件应该是无关的,并且无论初始化如何,都会达到全局最小值。即使对于非凸问题,也可以推测,只要初始化在同一个盆地中,算法就会收敛到相同的局部极小值。也就是说,我们希望,虽然一轮平均可能会产生一个合理的模型,但额外的一轮交流(和平均)不会产生进一步的改进。
图3显示了初始训练选择大的E值对莎士比亚LSTM问题的影响。事实上,对于非常大的本地epoch(1个epoch等于使用训练集中的全部样本训练一次),FedAvg可以是平稳的,也可以是发散的。这一结果表明,对于某些模型,特别是在收敛的后期阶段,用衰减学习率的方法衰减每轮的局部计算量(移动到更小的E或更大的B)可能是有用的。附录A中的图8给出了MNIST CNN的类似实验。有趣的是,对于这个模型,我们看不到大数值的E对收敛速度的显著下降。但是,对下面描述的大规模语言建模任务(参见附录A中的图10),我们看到E=1的性能略好于E=5。
CIFAR experiments 我们还对CIFAR-10数据集[24]进行了实验,以进一步验证FedAvg。数据集由10类32x32的RGB图像组成。我们将50000个训练样例和10000个测试样例分成100个客户机,每个客户机包含500个训练样例和100个测试样例;由于此数据没有自然的用户划分,因此我们考虑了平衡和IID设置。模型架构取自TensorFlow教程[38],该模型由两个卷积层、两个全连接的层和一个线性转换层组成,以生成总共约106个参数的逻辑。请注意,最先进的方法已经达到了CIFAR的96.5%[19]的测试精度;然而,我们使用的标准模型足以满足我们的需要,因为我们的目标是评估我们的优化方法,而不是在这项任务上实现可能的最佳精度。图像作为训练输入管道的一部分进行预处理,包括将图像裁剪为24x24,随机左右翻转,调整对比度、亮度和白化。

对于这些实验,我们考虑了一个额外的基线,即全训练集(无用户划分)上的标准SGD训练,使用大小为100的小批量。在197500个小批量更新之后,我们获得了86%的测试精度(每个小批量更新都需要在联邦设置中进行通信)。FedAvg仅在2000次通信轮次后达到了85%的类似测试精度。对于所有算法,除了初始学习速率外,我们还调整了学习速率衰减参数。表3给出了基线SGD、FedSGD和FedAvg达到三个不同精度目标的通信次数,图4给出了FedAvg与FedSGD的学习率曲线。

通过对SGD和FedAvg运行B=50的小批量实验,我们还可以将精度视为此类小批量梯度计算数量的函数。我们期望SGD在这里做得更好,因为在每一个小批量计算之后都会有一个连续的步骤。然而,如附录中的图9所示,对于C和E的适度值,FedAvg在每一个小批量计算中都有类似的进展。此外,我们发现每轮只有一个客户机的标准SGD和FedAvg(C=0)在精度上表现出显著的振荡,而对更多客户机的平均则可以消除这种振荡。

Large-scale LSTM experiments 我们对一个大规模的下一个单词预测任务进行了实验,以证明我们的方法在现实问题上的有效性。我们的训练数据集包括来自大型社交网络的1000万个公共邮件。我们按作者对这些邮件进行分组,总共有50多万个客户。此数据集是用户移动设备上存在的文本输入数据类型的现实代理。我们将每个客户数据集限制在最多5000个字,并在来自不同(非训练)作者的1e5邮件测试集上报告准确性(在10000个可能性中,预测概率最高的数据部分在正确的下一个词上)。我们的模型是一个256节点的LSTM,词汇表上有10000个单词。每个字的输入和输出嵌入尺寸为192,并与模型共同训练,共有4950544个参数。我们用了10个单词展开。
这些实验需要大量的计算资源,因此我们没有彻底地探索超参数:所有的实验都在每轮200个客户机上进行;FedAvg使用B=8和E=1。我们研究了FedAvg和基线FedSGD的各种学习率。图5显示了最佳学习率的单调学习曲线。η=18.0的FedSGD需要820轮才能达到10.5%的精度,而η=9.0的FedAvg仅在35个通信轮次中达到10.5%的精度(比FedSGD少23倍)。我们观察到FedAvg的测试精度差异较低,见附录A中的图10。该图还包括E=5的结果,该结果比E=1稍差。
4 Conclusions and Future Work
我们的实验表明,联邦学习是可行的,因为FedAvg使用相对较少的通信轮次来训练高质量的模型,正如在各种模型结构上的结果所证明的那样:一个多层感知器,两个不同的卷积NNs,一个两层字符LSTM和大规模的字级LSTM。
虽然联邦学习提供了许多实际的隐私好处,但通过差异隐私[14、13、1]提供更强大的保证,安全的多方计算[18]或它们的组合是未来工作的一个有趣方向。请注意,这两类技术最自然地应用于同步算法,如FedAvg。
References
[1] Martin Abadi, Andy Chu, Ian Goodfellow, Brendan McMahan, Ilya Mironov, Kunal Talwar, and Li Zhang. Deep learning with differential privacy. In 23rd ACM Conference on Computer and Communications Security (ACM CCS), 2016.
[2] Monica Anderson. Technology device ownership: 2015. http://www.pewinternet.org/2015/10/29/technology-device-ownership-2015/, 2015.
[3] Yossi Arjevani and Ohad Shamir. Communication complexity of distributed convex learning and optimization. In Advances in Neural Information Processing Systems 28. 2015.
[4] Maria-Florina Balcan, Avrim Blum, Shai Fine, and Yishay Mansour. Distributed learning, communication complexity and privacy. arXiv preprint arXiv:1204.3514, 2012.
[5] Yoshua Bengio, R´ejean Ducharme, Pascal Vincent, and Christian Janvin. A neural probabilistic language model. J. Mach. Learn. Res., 2003.
[6] Keith Bonawitz, Vladimir Ivanov, Ben Kreuter, Antonio Marcedone, H. Brendan McMahan, Sarvar Patel, Daniel Ramage, Aaron Segal, and Karn Seth. Practical secure aggregation for federated learning on user-held data. In NIPS Workshop on Private Multi-Party Machine Learning, 2016.
[7] David L. Chaum. Untraceable electronic mail, return addresses, and digital pseudonyms. Commun. ACM, 24(2), 1981.
[8] Jianmin Chen, Rajat Monga, Samy Bengio, and Rafal Jozefowicz. Revisiting distributed synchronous sgd. In ICLR Workshop Track, 2016.
[9] Anna Choromanska, Mikael Henaff, Micha¨el Mathieu, G´erard Ben Arous, and Yann LeCun. The loss surfaces of multilayer networks. In AISTATS, 2015.
[10] Greg Corrado. Computer, respond to this email. http://googleresearch.blogspot.com/2015/11/computer-respond-to-this-email.html, November 2015.
[11] Yann N. Dauphin, Razvan Pascanu, C¸ aglar G¨ulc¸ehre, KyungHyun Cho, Surya Ganguli, and Yoshua Bengio. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. In NIPS, 2014.
[12] Jeffrey Dean, Greg S. Corrado, Rajat Monga, Kai Chen, Matthieu Devin, Quoc V. Le, Mark Z. Mao, Marc’Aurelio Ranzato, Andrew Senior, Paul Tucker, Ke Yang, and Andrew Y. Ng. Large scale distributed deep networks. In NIPS, 2012.
[13] John Duchi, Michael I. Jordan, and Martin J. Wainwright. Privacy aware learning. Journal of the Association for Computing Machinery, 2014.
[14] Cynthia Dwork and Aaron Roth. The Algorithmic Foundations of Differential Privacy. Foundations and Trends in Theoretical Computer Science. Now Publishers, 2014.
[15] Olivier Fercoq, Zheng Qu, Peter Richt´arik, and Martin Tak´ac. Fast distributed coordinate descent for nonstrongly convex losses. In Machine Learning for Signal Processing (MLSP), 2014 IEEE International Workshop on, 2014.
[16] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning. Book in preparation for MIT Press, 2016.
[17] Ian J. Goodfellow, Oriol Vinyals, and Andrew M. Saxe. Qualitatively characterizing neural network optimization problems. In ICLR, 2015.
[18] Slawomir Goryczka, Li Xiong, and Vaidy Sunderam. Secure multiparty aggregation with differential privacy: A comparative study. In Proceedings of the Joint EDBT/ICDT 2013 Workshops, 2013.
[19] Benjamin Graham. Fractional max-pooling. CoRR, abs/1412.6071, 2014. URL http://arxiv.org/abs/1412.6071.
[20] Sepp Hochreiter and J¨urgen Schmidhuber. Long shortterm memory. Neural Computation, 9(8), November 1997.
[21] Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML, 2015.
[22] Yoon Kim, Yacine Jernite, David Sontag, and Alexander M. Rush. Character-aware neural language models. CoRR, abs/1508.06615, 2015.
[23] Jakub Koneˇcn´y, H. Brendan McMahan, Felix X. Yu, Peter Richtarik, Ananda Theertha Suresh, and Dave Bacon. Federated learning: Strategies for improving communication efficiency. In NIPS Workshop on Private Multi-Party Machine Learning, 2016.
[24] Alex Krizhevsky. Learning multiple layers of features from tiny images. Technical report, 2009.
[25] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS. 2012.
[26] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 1998.
[27] Chenxin Ma, Virginia Smith, Martin Jaggi, Michael I Jordan, Peter Richt´arik, and Martin Tak´aˇc. Adding vs. averaging in distributed primal-dual optimization. In ICML, 2015.
[28] Ryan McDonald, Keith Hall, and Gideon Mann. Distributed training strategies for the structured perceptron. In NAACL HLT, 2010.
[29] Natalia Neverova, Christian Wolf, Griffin Lacey, Lex Fridman, Deepak Chandra, Brandon Barbello, and Graham W. Taylor. Learning human identity from motion patterns. IEEE Access, 4:1810–1820, 2016.
[30] Jacob Poushter. Smartphone ownership and internet usage continues to climb in emerging economies. Pew Research Center Report, 2016.
[31] Daniel Povey, Xiaohui Zhang, and Sanjeev Khudanpur. Parallel training of deep neural networks with natural gradient and parameter averaging. In ICLR Workshop Track, 2015.
[32] William Shakespeare. The Complete Works of William Shakespeare. Publically available at https://www.gutenberg.org/ebooks/100.
[33] Ohad Shamir and Nathan Srebro. Distributed stochastic optimization and learning. In Communication, Control, and Computing (Allerton), 2014.
[34] Ohad Shamir, Nathan Srebro, and Tong Zhang. Communication efficient distributed optimization using an approximate newton-type method. arXiv preprint arXiv:1312.7853, 2013.
[35] Reza Shokri and Vitaly Shmatikov. Privacy-preserving deep learning. In Proceedings of the 22Nd ACM SIGSAC Conference on Computer and Communications Security, CCS ’15, 2015.
[36] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural networks from overfitting. 15, 2014.
[37] Latanya Sweeney. Simple demographics often identify people uniquely. 2000.
[38] TensorFlow team. Tensorflow convolutional neural networks tutorial, 2016. http://www.tensorflow.org/tutorials/deep_cnn.
[39] White House Report. Consumer data privacy in a networked world: A framework for protecting privacy and promoting innovation in the global digital economy. Journal of Privacy and Confidentiality, 2013.
[40] Tianbao Yang. Trading computation for communication: Distributed stochastic dual coordinate ascent. In Advances in Neural Information Processing Systems, 2013.
[41] Ruiliang Zhang and James Kwok. Asynchronous distributed admm for consensus optimization. In ICML. JMLR Workshop and Conference Proceedings, 2014.
[42] Sixin Zhang, Anna E Choromanska, and Yann LeCun. Deep learning with elastic averaging sgd. In NIPS. 2015.
[43] Yuchen Zhang and Lin Xiao. Communication-efficient distributed optimization of self-concordant empirical loss. arXiv preprint arXiv:1501.00263, 2015.
[44] Yuchen Zhang, Martin J Wainwright, and John C Duchi. Communication-efficient algorithms for statistical optimization. In NIPS, 2012.
[45] Yuchen Zhang, John Duchi, Michael I Jordan, and Martin J Wainwright. Information-theoretic lower bounds for distributed statistical estimation with communication constraints. In Advances in Neural Information Processing Systems, 2013.
[46] Martin Zinkevich, Markus Weimer, Lihong Li, and Alex J. Smola. Parallelized stochastic gradient descent. In NIPS. 2010.




