Soft-to-Hard Vector Quantization for End-to-End Learning Compressible Representations
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!
Abstract:
我们提出了一种新的方法,通过端到端的训练策略来学习深度架构中的可压缩表征。我们的方法是基于量化和熵的软(连续)松弛,我们在整个训练过程中对它们的离散对应体进行了退火。我们在两个具有挑战性的应用中展示了这种方法:图像压缩和神经网络压缩。虽然这些任务通常是用不同的方法来处理的,但我们的软量化到硬量化方法给出的结果与这两种方法的最先进水平具有可比性。
1 Introduction:
近年来,深度神经网络(DNNs)在机器学习和计算机视觉方面取得了许多突破性的成果[20,28,9],目前已广泛应用于工业领域。现代DNN模型通常有数百万或数千万个参数,导致无论是在他们生成的中间特征表示,还是在模型本身中,都存在高度冗余的结构。尽管DNN模型的过度参数化对训练有良好的影响,但在实践中,通常需要压缩DNN模型进行推理,例如在内存有限的移动或嵌入式设备上部署它们时。另一方面,学习可压缩表征的能力在为各种数据类型(如图像、音频、视频和文本)开发(数据自适应)压缩算法方面具有很大的潜力,这些数据类型现在都有各种DNN架构可用。
DNN模型压缩和利用DNN进行有损图像压缩是近年来引起广泛关注的两种方法。为了压缩一组连续的模型参数或特征,我们需要从一组量化级别(或矢量,在多维情况下)中选一个代表来近似每个参数或特征,其中每个量化级别与一个符号相关联,然后存储参数或特征的符号表示,以及量化级别。用相应的量化水平来表示一个DNN模型的每个参数或特征,将以失真D为代价,即性能损失(例如,量化模型参数后分类DNN的分类精度,或量化中间特征表示的自动编码器内容中的重构错误)。码率R,即符号流的熵,决定了编码比特流中模型或特征的成本。
为了学习可压缩的DNN模型或特征表示,我们需要最小化D+βR,其中β>0控制率失真的权衡。将熵包含到学习成本函数中可以看作是添加了一个正则化器,它促进了网络的可压缩表示或紧凑特征表示。然而,在将DNNs的D+βR最小化时,会遇到两个主要的挑战:i)处理成本函数D+βR的不可微性(由于量化操作),以及ii)获得熵的精确可微估计(即R)。为了解决问题i),学界提出了许多方法,其中最流行的是随机近似[39,19,6,32,4]和四舍五入光滑导数近似[15,30]。要解决ii),一个常见的方法是假设符号流为i.i.d.,并用参数模型(如高斯混合模型[30,34]、分段线性模型[4]或伯努利分布[33](如为二进制符号)对边缘符号分布进行建模。

在本文中,我们提出了一个统一的端到端学习框架,用于学习可压缩表征,联合优化模型参数、量化水平和由此产生的符号流的熵,以压缩网络或模型本身(见插图)。我们在DNN模型和特征压缩中用新颖的方法来解决上述的挑战i)和ii)。我们的主要贡献是:
- 我们提供了第一个关于特征表示和DNN模型的端到端学习压缩的统一方案。到目前为止,这两个问题在文献中基本上是独立研究的。
- 我们的方法简单直观,依赖于给定标量或矢量的软分配来量化到各个量化级别。用参数控制分配的“硬度”,并允许在训练期间逐步从软分配过渡到硬分配。与基于四舍五入或随机量化的方案相比,我们的编码方案是直接可微的,因此是可训练的端到端方案。
- 我们的方法并不强制网络适应特定的(给定的)量化输出(例如整数),而是与权重一起学习量化级别,从而使其能够应用于更广泛的问题集。特别是,我们首次在所学压缩的背景下探索矢量量化,并证明其优于标量量化。
- 与之前的所有工作不同,我们不假设特征或模型参数的边缘分布,这些特征或模型参数是通过依赖于分配概率的柱状图而量化的,而不是文献中常用的参数模型。
- 我们将我们的方法应用于32层ResNet模型[13]的DNN模型压缩,并结合最近在[30]中提出的压缩自动编码器的变体来实现全分辨率图像压缩。在这两种情况下,我们都取得了与最先进技术相当的性能,同时与原始作品相比,我们做了更少的模型假设,并显著简化了训练程序[30,5]。
论文的其余部分组织如下。第2节回顾了相关工作,在第3节介绍从软到硬的矢量量化方法。然后,我们分别在第4节和第5节中将其应用于压缩自动编码器进行图像压缩和ResNet进行DNN压缩。第6节总结全文。
2 Related Work
人们对全分辨率图像压缩的DNN模型的兴趣激增,最显著的是[32,33,3,4,30],所有这些模型都优于JPEG[35],一些甚至超过了JPEG 2000[29],开创性的工作[32,33]表明,可通过卷积循环神经网络(RNNs)学习渐进式图像压缩,在训练过程中采用随机量化方法。[3,30]都依赖卷积自动编码器架构。这些工作将在第4节中进行更详细的讨论。
在DNN模型压缩的背景下,一系列工作[12,11,5]采用一个多步骤的过程,先对预训练DNN的权重进行修剪,然后使用类似k-means的算法对剩余的参数进行量化,接着对DNN进行再约束,最后对量化后的DNN模型进行熵编码。[34]提出了一种值得注意的不同方法,使用最小描述长度原则来处理DNN压缩任务,其具有坚实的信息理论基础。
值得注意的是,许多最近工作的目标都是对DNN模型参数以及特征表示进行量化,用于加速在硬件上低精度算法的DNN评估,参见[15,23,38,43]。然而,这些工作中的大多数并没有专门训练DNN,因此量化参数在信息论意义上是可压缩的。
在优化过程中,从一个简单(凸或可微)问题逐渐过渡到实际的困难问题,正如我们在软量化到硬量化框架中所做的那样,已经在不同的环境中进行了研究,并且属于连续方法的范畴(参见[2]以获得概述)。形式上相关,但从概率角度出发的是用于最大熵聚类/矢量量化的确定性退火方法,参见,例如[24,42]。可以说,与我们的方法最相关的是[41],它也使用了最近邻分配的拓展,但是在学习监督原型分类器的上下文中。据我们所知,在神经网络图像压缩或DNN压缩的端到端学习框架中,以前没有采用连续方法。
3 Proposed Soft-to-Hard Vector Quantization
3.1 Problem Formulation





L个中心矢量,维度为d/m,将d维的特征转化为[L]m;原始特征z由m个d/m维的矢量构成,每个矢量选择采用最近邻算法。

由于带参数σ的softmax操作可以找到最近邻,当σ趋向于正无穷的时候,对应标签即为1,这就是硬分配;σ表示分配的硬度。



4 Image Compressin
现在我们展示如何使用我们的框架来实现一个简单的图像压缩系统。对于其结构,我们使用了[30]中最近提出的卷积自动编码器的变体(详细信息请参见附录A.1)。我们注意到,当我们使用[30]的结构时,我们使用软到硬的熵最小化方法对其进行训练,这与原方法有很大的不同,见下文。
我们的目标是学习自动编码器瓶颈中的特性的可压缩表示。因为我们不希望来自不同瓶颈通道的特征同分布,所以我们用不同的直方图和熵损失对每个通道的分布进行建模,并使用相同的参数β将每个熵项添加到总损失中。为了将通道编码成符号,我们将通道矩阵分为pw x ph维的片序列。这些片(矢量化)形成Z属于Rd/m x m的列,其中m=d/(pwph),因此Z包含m(pwph)维的点。当ph或pw大于1时,符号可以捕获瓶颈中的局部相关性,这是可取的,因为我们将符号建模为独立同分布的随机变量来进行熵编码。然后,在测试时,符号编码器E通过在一组L中心矢量C(C包含于Rpwph)上执行最近邻分配来确定信道中的符号,从而产生^ z。在训练过程中,我们使用了软量化的~z,以及w.r.t.中心矢量C。
我们使用Adam[17]训练不同的模型,见附录A.2。我们的训练集与[3]中描述的训练集组成类似。我们使用了ImageNet[8]中90000张图像的子集,我们用系数0.7对其进行了下采样,并对128 x 128像素的片进行了训练,批大小为15。为了估计优化(8)的概率分布p,我们在5000多个图像上保持一个直方图,每10次迭代更新一次当前批次的图像。有关其他超参数的详细信息,请参见附录A.2。

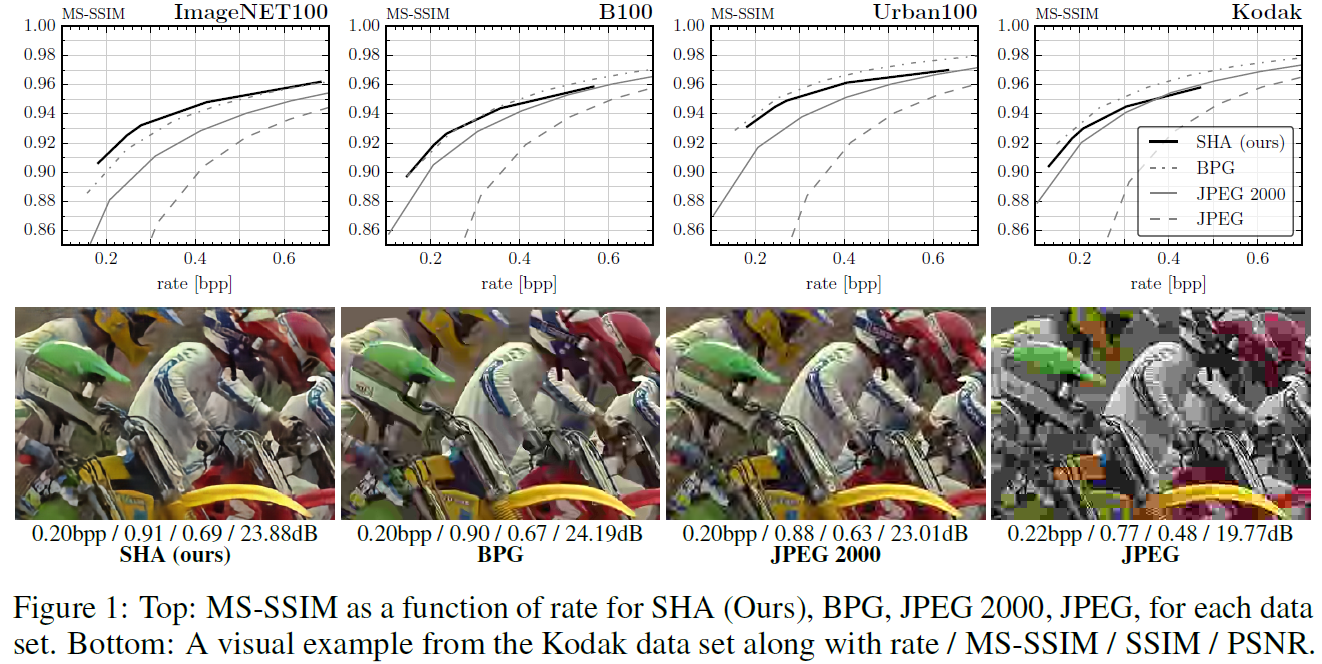
Evaluation. 为了评估我们的软-硬自动编码器(SHA)方法的图像压缩性能,我们使用了四个数据集,即Kodak[1],B100[31],Urban100[14],ImageNet100(100个从ImageNet[25]随机选择的图像)和三个标准质量度量,即峰值信噪比(PSNR)、结构相似性指数(SSIM)[37]和多尺度SSIM(MS-SSIM),详见附录A.5。我们将我们的SHA与标准的JPEG、JPEG 2000和BPG[10]进行了比较,重点放在压缩率小于1比特每像素(bpp)(即传统的基于积分变换的压缩算法最受挑战的情况)。如图1所示,对于高压缩率(小于0.4 bpp),我们的SHA在MS-SSIM方面优于JPEG和JPEG 2000,并且与BPG竞争。可以观察到SSIM也存在类似趋势(有关作为bpp函数的SSIM和PSNR图,请参见附录A.6中的图4)。与JPEG 2000相比,SHA在ImageNet100上的表现最好,在Kodak上的挑战最大。从视觉上看,SHA压缩图像的伪影比JPEG 2000压缩图像的伪影少(见图1和附录A.7)。
Related methods and discussion. JPEG 2000[29]使用基于小波变换和自适应EBCOT编码。BPG[10]基于HEVC视频压缩标准的一个子集,是图像压缩的最新技术。它使用上下文自适应二进制算术编码(CABAC)[21]。
最近的工作[30,4]也显示出了与JPEG 2000的相当性能。虽然我们使用了[30]的结构,但这些工作之间存在着明显的差异,相关总结在插图表格中。[4]的工作使用多个广义除数归一化(GDN)层及其逆矩阵(IGDN)构建了一个深度模型,这是专门设计用来捕获自然图像局部联合统计信息的层。此外,他们使用线性样条对熵估计的边缘进行建模,并使用CABAC[21]编码。在这段时间,[16]的方法建立在[33]中提出的结构的基础上,并表明通过将MS-SSIM度量合并到优化中(而不仅仅是最小化MSE),可以获得令人印象深刻的MS-SSIM度量性能。

与这些最先进的方法所采用的领域特定技术相比,我们的学习可压缩表示的框架可以实现有竞争力的图像压缩系统,只需使用卷积自动编码器和简单的熵编码。
5 DNN Compression
对于DNN压缩,我们研究了用于图像分类的ResNet[13]体系结构。我们采用与[5]相同的设置,并考虑为CIFAR-10[18]训练的32层体系结构。如[5]所示,我们的目标是学习模型所有464154可训练参数的可压缩表示。

我们的可压缩模型在使用哈夫曼编码达到压缩因子19.15和使用算术编码达到压缩因子20.15的同时,达到了92.1%的测试精度。表1将我们的结果与[5]报告的最新方法进行了比较。我们注意到,尽管文献中的顶级方法也达到了92%以上的精度和20%以上的压缩因子,但它们采用了大量手工设计的步骤,如修剪、重训练、各种类型的权重聚类、采用特殊编码将稀疏权重矩阵编码为基于索引差分的格式,最后采用熵编码。相反,我们直接最小化训练中权重的熵,得到一种使用标准熵编码的高度可压缩的表示法。

在附录A.8的图5中,我们展示了随着网络学习在优化(6)时将大部分权重压缩到几个中心,样本熵H(p)是如何在训练过程中衰减的,以及索引柱状图是如何发展的。相比之下,使用[12,11,5]的方法,通过修剪大约80%的网络权重,手动将0作为最频繁的中心。我们注意到[34]最近的工作还通过使用最小描述长度原则,在单个训练过程中解决了这个问题。与我们的框架相比,它们采用贝叶斯视角,并依赖于符号分布的参数假设。
6 Conclusions
在本文中,我们提出了一个统一的框架,用于端到端学习深层架构的压缩表示。通过软-硬退火方案的训练,逐步从样本熵的软松弛和网络离散化过程转移到实际的不可微量化过程,我们设法优化了原始网络损耗和熵之间的率失真权衡。我们的框架可以便捷地捕获不同的压缩任务,从而获得可以与最先进的图像压缩和DNN压缩相竞争的结果。我们方法的简洁性为将来的工作开辟了不同的方向,因为我们的框架可以很容易地适应其他需要可压缩表示的任务。
Refences
[1] Kodak PhotoCD dataset. http://r0k.us/graphics/kodak/, 1999.
[2] Eugene L Allgower and Kurt Georg. Numerical continuation methods: an introduction, volume 13. Springer Science & Business Media, 2012.
[3] Johannes Ballé, Valero Laparra, and Eero P Simoncelli. End-to-end optimization of nonlinear transform codes for perceptual quality. arXiv preprint arXiv:1607.05006, 2016.
[4] Johannes Ballé, Valero Laparra, and Eero P Simoncelli. End-to-end optimized image compression. arXiv preprint arXiv:1611.01704, 2016.
[5] Yoojin Choi, Mostafa El-Khamy, and Jungwon Lee. Towards the limit of network quantization. arXiv preprint arXiv:1612.01543, 2016.
[6] Matthieu Courbariaux, Yoshua Bengio, and Jean-Pierre David. Binaryconnect: Training deep neural networks with binary weights during propagations. In Advances in Neural Information Processing Systems, pages 3123–3131, 2015.
[7] Thomas M Cover and Joy A Thomas. Elements of information theory. John Wiley & Sons, 2012.
[8] J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, and L. Fei-Fei. ImageNet: A Large-Scale Hierarchical Image Database. In CVPR09, 2009.
[9] Andre Esteva, Brett Kuprel, Roberto A Novoa, Justin Ko, Susan M Swetter, Helen M Blau, and Sebastian Thrun. Dermatologist-level classification of skin cancer with deep neural networks. Nature, 542(7639):115–118, 2017.
[10] Bellard Fabrice. BPG Image format. https://bellard.org/bpg/, 2014.
[11] Song Han, Huizi Mao, and William J Dally. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv preprint arXiv:1510.00149, 2015.
[12] Song Han, Jeff Pool, John Tran, and William Dally. Learning both weights and connections for efficient neural network. In Advances in Neural Information Processing Systems, pages 1135–1143, 2015.
[13] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2016.
[14] Jia-Bin Huang, Abhishek Singh, and Narendra Ahuja. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5197–5206, 2015.
[15] Itay Hubara, Matthieu Courbariaux, Daniel Soudry, Ran El-Yaniv, and Yoshua Bengio. Quantized neural networks: Training neural networks with low precision weights and activations. arXiv preprint arXiv:1609.07061, 2016.
[16] Nick Johnston, Damien Vincent, David Minnen, Michele Covell, Saurabh Singh, Troy Chinen, Sung Jin Hwang, Joel Shor, and George Toderici. Improved lossy image compression with priming and spatially adaptive bit rates for recurrent networks. arXiv preprint arXiv:1703.10114, 2017.
[17] Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. CoRR, abs/1412.6980, 2014.
[18] Alex Krizhevsky and Geoffrey Hinton. Learning multiple layers of features from tiny images. 2009.
[19] Alex Krizhevsky and Geoffrey E Hinton. Using very deep autoencoders for content-based image retrieval. In ESANN, 2011.
[20] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pages 1097–1105, 2012.
[21] Detlev Marpe, Heiko Schwarz, and Thomas Wiegand. Context-based adaptive binary arithmetic coding in the h. 264/avc video compression standard. IEEE Transactions on circuits and systems for video technology, 13(7):620–636, 2003.
[22] D. Martin, C. Fowlkes, D. Tal, and J. Malik. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proc. Int’l Conf. Computer Vision, volume 2, pages 416–423, July 2001.
[23] Mohammad Rastegari, Vicente Ordonez, Joseph Redmon, and Ali Farhadi. Xnor-net: Imagenet classification using binary convolutional neural networks. In European Conference on Computer Vision, pages 525–542. Springer, 2016.
[24] Kenneth Rose, Eitan Gurewitz, and Geoffrey C Fox. Vector quantization by deterministic annealing. IEEE Transactions on Information theory, 38(4):1249–1257, 1992.
[25] Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, Alexander C. Berg, and Li Fei-Fei. ImageNet Large Scale Visual Recognition Challenge. International Journal of Computer Vision (IJCV), 115(3):211–252, 2015.
[26] Wenzhe Shi, Jose Caballero, Ferenc Huszár, Johannes Totz, Andrew P Aitken, Rob Bishop, Daniel Rueckert, and Zehan Wang. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1874–1883, 2016.
[27] Wenzhe Shi, Jose Caballero, Lucas Theis, Ferenc Huszar, Andrew Aitken, Christian Ledig, and Zehan Wang. Is the deconvolution layer the same as a convolutional layer? arXiv preprint arXiv:1609.07009, 2016.
[28] David Silver, Aja Huang, Chris J Maddison, Arthur Guez, Laurent Sifre, George Van Den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, et al. Mastering the game of go with deep neural networks and tree search. Nature, 529(7587):484–489, 2016.
[29] David S. Taubman and Michael W. Marcellin. JPEG 2000: Image Compression Fundamentals, Standards and Practice. Kluwer Academic Publishers, Norwell, MA, USA, 2001.
[30] Lucas Theis, Wenzhe Shi, Andrew Cunningham, and Ferenc Huszar. Lossy image compression with compressive autoencoders. In ICLR 2017, 2017.
[31] Radu Timofte, Vincent De Smet, and Luc Van Gool. A+: Adjusted Anchored Neighborhood Regression for Fast Super-Resolution, pages 111–126. Springer International Publishing, Cham, 2015.
[32] George Toderici, Sean M O’Malley, Sung Jin Hwang, Damien Vincent, David Minnen, Shumeet Baluja, Michele Covell, and Rahul Sukthankar. Variable rate image compression with recurrent neural networks. arXiv preprint arXiv:1511.06085, 2015.
[33] George Toderici, Damien Vincent, Nick Johnston, Sung Jin Hwang, David Minnen, Joel Shor, and Michele Covell. Full resolution image compression with recurrent neural networks. arXiv preprint arXiv:1608.05148, 2016.
[34] Karen Ullrich, Edward Meeds, and Max Welling. Soft weight-sharing for neural network compression. arXiv preprint arXiv:1702.04008, 2017.
[35] Gregory K Wallace. The JPEG still picture compression standard. IEEE transactions on consumer electronics, 38(1):xviii–xxxiv, 1992.
[36] Z. Wang, E. P. Simoncelli, and A. C. Bovik. Multiscale structural similarity for image quality assessment. In Asilomar Conference on Signals, Systems Computers, 2003, volume 2, pages 1398–1402 Vol.2, Nov 2003.
[37] Zhou Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing, 13(4):600–612, April 2004.
[38] WeiWen, ChunpengWu, YandanWang, Yiran Chen, and Hai Li. Learning structured sparsity in deep neural networks. In Advances in Neural Information Processing Systems, pages 2074–2082, 2016.
[39] Ronald J Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning, 8(3-4):229–256, 1992.
[40] Ian H. Witten, Radford M. Neal, and John G. Cleary. Arithmetic coding for data compression. Commun. ACM, 30(6):520–540, June 1987.
[41] Paul Wohlhart, Martin Kostinger, Michael Donoser, Peter M. Roth, and Horst Bischof. Optimizing 1-nearest prototype classifiers. In IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), June 2013.
[42] Eyal Yair, Kenneth Zeger, and Allen Gersho. Competitive learning and soft competition for vector quantizer design. IEEE transactions on Signal Processing, 40(2):294–309, 1992.
[43] Aojun Zhou, Anbang Yao, Yiwen Guo, Lin Xu, and Yurong Chen. Incremental network quantization: Towards lossless cnns with low-precision weights. arXiv preprint arXiv:1702.03044, 2017.
A Image Compression Details
A.1 Architecture
我们依赖于最近在[30]中提出的压缩自动编码器的变体,使用卷积神经网络对图像编码器和图像解码器进行编码。图像编码器中的前两个卷积层,每个卷积层将输入图像缩小一个因子2,并将通道数从3增加到128。接下来是三个残差块,每个块有128个过滤器。另一个卷积层然后再次减小一个因子2,并将通道数减少到c,其中c是一个超参数([30]使用64和96个通道)。对于w x h维的输入图像,图像编码器的输出为w/8 x h/8 x c维的“瓶颈张量”。



