数据结构 : 堆之外传

缘起

这篇不讲并行/并发。

C 语言宗师级人物 Rob Pike 在 Notes on C Programming 文章中阐述了他对软件复杂性的理解，并给出了以下几个原则。

原则1：

你无法断定程序会在哪花费更多时间。瓶颈往往出现在意料不到的地方，所以不要急于猜测并修改之，除非你可以证实这就是瓶颈所在。

原则2：

仔细估量。在你还没有对代码仔细估量前，不要进行速度优化。除非这部分代码相较其余部分拥有压倒性优势。

原则3：

当 n 很小的时候，花哨的算法都很慢，而 n 通常很小。花哨的算法通常还会有较大的常数。除非你确定 n 会经常变得很大，否则不要使用花哨的算法（即便 n 真的很大，也要首先考虑原则2）。比如，对于 workaday 问题，二叉树总是比伸展树更快。

【译注：这是个什么问题？持续工作问题？伸展树支持二叉查找树的所有操作，但不保证 O(logN) 的最坏情况性能。它的上限是均摊的。如果访问模式非随机，在实际中伸展树似乎执行的更好。因为伸展使得 find 操作很昂贵，所以当访问序列随机且均匀分布时，伸展树没有其他平衡树好。总而言之，伸展树还不适合在实际中使用。】

原则4：

花哨的算法比起简单算法来，更容易出 Bug ，而且实现起来更困难。尽量使用简单的算法和简单的数据结构。

几乎所有的程序都会使用以下数据结构：

数组
链表
散列表
二叉树

当然，你可能也会混合这些数据结构来用。比如，编译器用到的符号表或许由散列表来实现，而散列表又包含有字符串数组的链表。

原则5：

数据压倒一切。如果你选择了正确的数据结构并组织的井井有条，那么算法也就不言自明。数据结构是编程的核心，而不是算法。

原则6：

没有原则6。^_^

瞎侃

从原则5知道数据结构的重要了吧，吼吼。不再废话，直接进入本文主题。

堆是古往今来唯一被泱泱中华的文人骚客们题诗作赋过的数据结构。什么，看官您不信？咱可有诗为证。诗曰：

Heap啊，Heap，
上头尖来下头粗。
有朝一日倒过来，
下头尖来上头粗。

看官您又有高论了？嗯...，上头尖来下头粗？这分明就是一坨嘛。咳咳...，看官您的观点还真...别致。总而言之呢，堆就是上头尖来下头粗的...一坨。

堆实际上是一棵完全二叉树。为了维持“上头尖来下头粗”的形状和有序性，我们规定老子要在儿子的上面，而且比儿子的键值要小。丫丫个呸，这简直就是大头儿子小头爸爸嘛。这样，它和二叉查找树比较起来有个好处，就是假如你想知道堆中“头”最小的爸爸是谁，压根不用找，最顶上那个就是。毛主席教导我们，看问题要一分为二。凡事有好就有坏，堆所带来的坏处就是除了可以很轻松的查找堆中最小值外，基本上不能做别的了。当然，插入和删除这种基本操作还是可以做的。

堆的插入操作就是暂时认为要插入的值是“头”最大的儿子，把它先放入最下层下一个可用位置上。然后让其与老子比较，看谁的“头”大。持续这个过程，让其一直朝着最顶层的根祖宗方向往上冒，直到找到合适位置。这个过程称为“percolate up”。

而删除操作则反其道而行之。我们知道，找到最小项很容易，难点在于如何删除它。当最小项“死亡”后，我们会发现，在根位置找不到“头”最小的祖宗了，形成了一个空结点。这还了得。为了维持“上头尖来下头粗”的形状，我们得找个祖宗放到该位置。于是我们把堆中最后一项放入空结点。如果最后一项应该放在这，操作就完成了。然而，这几乎不可能，除非堆的大小是2或3。那么只能沿着儿子结点往下移动了。但是有两个儿子哎，选哪个？废话，当然是选“头”较小的那个啦，这样才显得像父子，看见“大头”就来气。就这样，一直移动到合适位置。这个过程则称为“percolate down”。

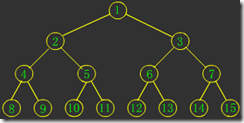
那我们该怎么找父亲儿子呢？这就得依靠完全二叉树的特性了。完全二叉树是完全填满的树，只有最底层可能有例外。最底层按从左到右的次序填入，中间不能有空结点。如图所示：

图1

图2

图3

图4

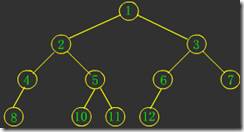
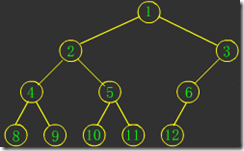
图1是一棵满二叉树；图2是一棵完全二叉树；图3和图4都不是完全二叉树，因为这两个中间都有空结点。很显然，满二叉树也是完全二叉树。看看图1和图2是不是很像“上头尖来下头粗”的一坨，:-)。

完全二叉树有许多有用的特性。比如，N个结点的完全二叉树的高度至多是 logN 。不需要 left 和 right 链接等。这样，我们可以将一棵完全二叉树以按层遍历的次序存储在数组中（这符合原则4）。我们把根祖宗放入数组索引 1 的位置，其他结点依次放入。为什么不放在索引 0 呢？因为除了根结点外，每个结点都有父节点。为了避免特殊情况，我们保留位置 0 为哑结点，使其可以当作根结点的父亲。此外，还有其他好处，不再一一列举。这样，我们对数组中任意索引 i 的结点，均可以在索引 2i 处找到它的左儿子。如果该位置超出了树中结点数，那我们就知道它没有左儿子。同理，它的右儿子在索引 2i+1 处。当然，我们也要测试其是否存在。它老子则在 i/2 索引处。

如果只需要插入，删除和找最小值三种操作，那么我们应该毫不犹豫的使用堆。那什么时候会有这种情况？比方说，喜欢我的MM有一个加强排。这么多人每天都围在你身边嗡嗡来嗡嗡去，咋应付啊？于是，我定个标准：每次，我都只找队伍里面最清纯的MM。这下，整个世界清净了。以后，当遇见新美女时，就把她放到队伍合适的位置。那些跟咱Say 88的MM，则一概从队伍里面开除。这个时候，这个队伍用堆来排列最合适不过。这听起来好像优先级队列啊。没错，堆还有一个别名，正是优先级队列。

很遗憾，.NET并没有提供优先级队列集合。我们只能自己编写，下面是完整源代码。