结对项目
结对编程
| 软件工程 | 网工1934 |
|---|---|
| 作业要求 | 作业要求 |
| 作业目标 | 实现一个自动生成小学四则运算题目的命令行程序 |
陈卓鸿 3119005320
张栩 3119005350
Github项目链接
一. PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| - Estimate | 估计这个任务需要多少时间 | 970 | 1100 |
| Development | 开发 | ||
| - Analysis | 需求分析(包括学习新技术) | 100 | 100 |
| - Design Spec | 生成设计文档 | 40 | 50 |
| - Desgin Review | 设计复审 | 30 | 30 |
| - Coding Standard | 代码规范(为目前的开发指定合适的规范) | 60 | 80 |
| - Desgin | 具体设计 | 50 | 100 |
| - Coding | 具体编码 | 300 | 300 |
| - Code Review | 代码复审 | 60 | 60 |
| - Test | 测试(自我测试,修改代码,提交修改) | 200 | 300 |
| Reporting | 报告 | ||
| - Test Repor | 测试报告 | 50 | 50 |
| - Size Measurement | 计算工作量 | 20 | 20 |
| - Postmortem & Process Improvement Plan | 事后总结,并提出过程改进计划 | 60 | 60 |
| 总结 | 970 | 1100 |
二. 需求分析
| 类名 | 功能 |
|---|---|
| EquationHandler | 主启动类 |
| Equation | 四则运算的基本算式类 |
| EquationUtils | 算式的处理工具类,包括生成算式和检查 |
| ElementUtils | 算式中的元素判断和处理类,元素包括运算数和运算符等 |
| CalculateUtils | 算式计算类,包括对算式转换为逆波兰式和别的四则运算 |
| AccessUtils | 文件存取类,负责读写文件 |
| RandomUtils | 随机数生成器类,生成随机运算数和运算符 |
三. 效能分析
耗时1
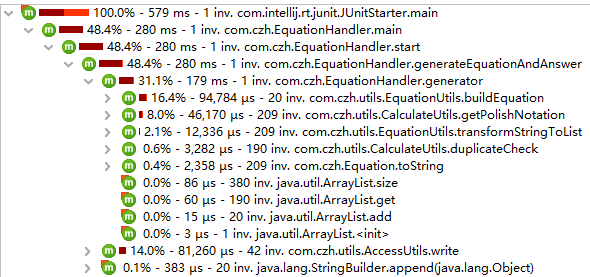
耗时2
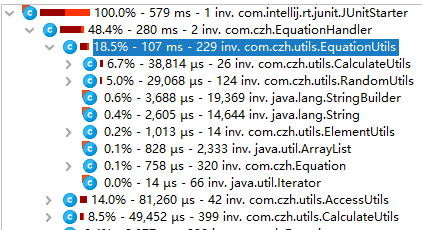
耗内存1
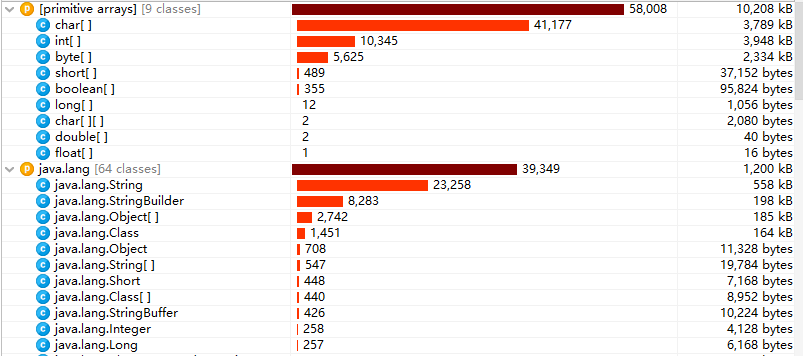
耗内存2
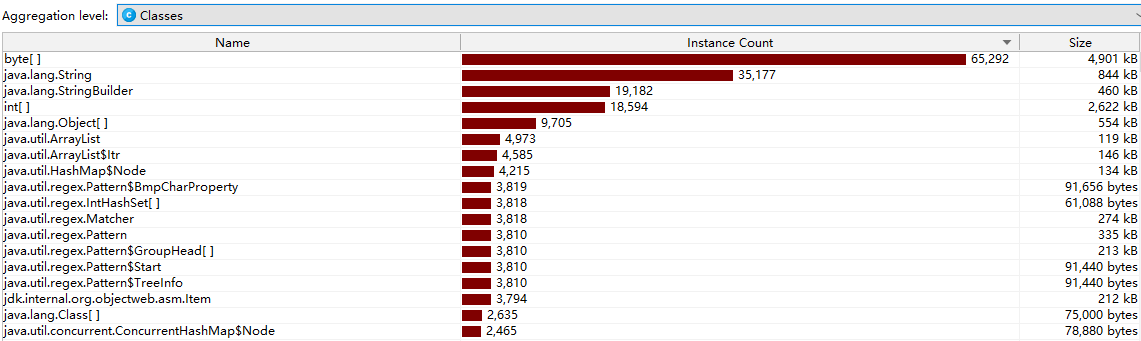
四. 设计说明
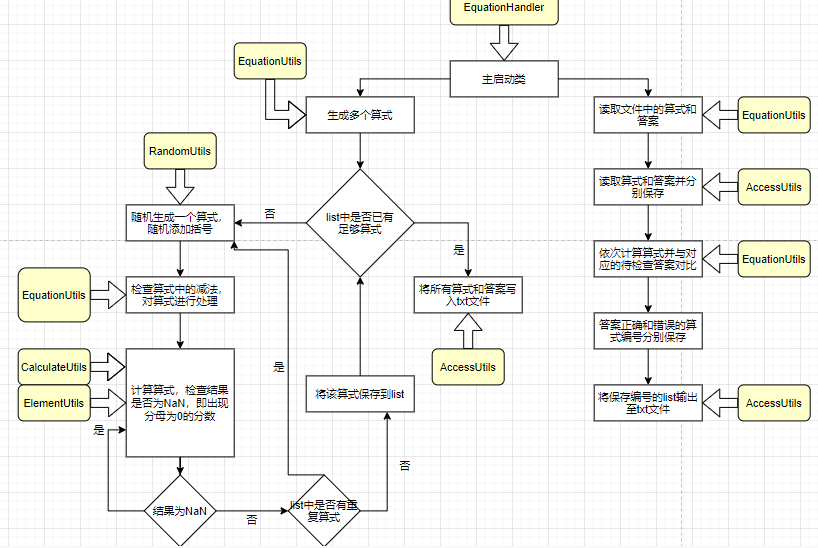
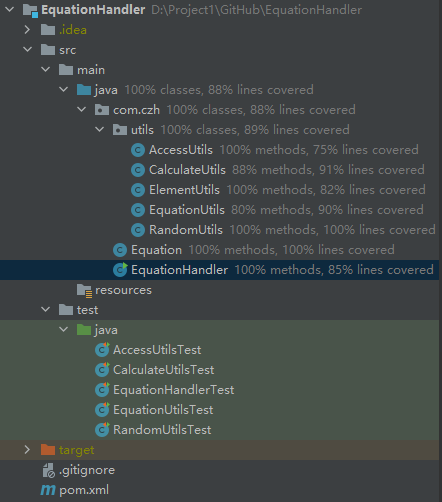
1.算式实体类Equation
Java中String作为不可变对象,不方便处理,因此:
- Equation中使用
ArrayList<String>作为底层存储方式,运算数和运算符以String存放在其中 - 需要将Equation转换为String时,依次获取list中的元素通过StringBuilder生成字符串即可
2.减法检查方法checkMinus
该项目减法检查为生成算式后对算式进行处理,而不是在生成的过程中检查
- 减法可能出现的情况
设a,b为运算数,(...)为子算式 -
a-b如2/3 - 4
-
a-(...)如1-(4/5-3)
-
(...)-b如(1/3-1)-2
-
(...)-(...)如(1-2)-(3-4)
- 对输入的算式从左到右进行查找减号
- 获取减号两边的运算数,记录左运算数和右运算数的下标(此时该减法为子算式)
- 对运算数进行比较(不进行计算),若左运算数小于右运算数,则调换两数位置
- 若右运算数是一个复杂的子算式,则将右运算数作为本方法的参数,递归进行减法检查,检查完后计算结果(此时右运算数的结果一定大于0)并返回,左运算数再与结果进行比较
- 若结果小于0,则通过处理第二步的下标,将处理后的子算式替换原下标的子算式;若结果大于0,则原来位置的子算式不改变
- 补充
由于算式从左到右检查,左运算数实际已经检查过,因此第4步不必检查左运算数
获取减号两边的运算数
同位置上, +和-可替换,×和÷可替换
- 减号左边的运算数情况
a-b运算数为aa×(b+c)-d运算数为a×(b+c)(a+b)×c-d运算数为(a+b)×c
3.计算模块
生成的算式为中缀表达式,由于我们的实现思路需要将运算数和运算符存入List中,如果存入中缀表达式的话并不方便计算,而将中缀表达式转换为后缀表达式(即逆波兰式)以后能有效地简化计算问题,而且也方便生成题目时查重的判断。
- 逆波兰表示法是波兰逻辑学家J・卢卡西维兹(J・ Lukasewicz)于1929年首先提出的一种表达式的表示方法。后来,人们就把用这种表示法写出的表达式称作“逆波兰表达式”。逆波兰表达式把运算量写在前面,把算符写在后面。例如:[1, 2, 3, +, -,它等价于1-(2+3)。]
参考资料和实现方法:
分数处理
由于运算数以String的形式存储,因此我们判断是否为分数只需要判断字符串中是否存在带分数符号" ' "和分数符号" / ",如1'2/3和4/5都是分数类型
注:若计算时输入的字符串为负数,类似-3,会识别为分数类型,但是在转换分数时会抛出异常,因为该字符串中不存在带分数符号和分数符号
负数处理和无穷大处理
若计算中出现负数,假设有某种减法情况没有处理导致结果出现负数,或者计算过程中出现了分母为0的分数(除数为0的除法)导致结果会无穷大,则计算方法Calculate不会再往下执行,而是立即返回字符串"NaN"
若外层方法检查到Calculate方法返回"NaN",会循环重新生成算式,直至结果不再为"NaN",然后将新生成的算式替代原算式
题目查重
经过逆波兰式处理后,我们将得到的后缀表达式中的运算数和运算符按序存入List中。按照题目的要求,对于重复的题目的定义是完全相同的运算数、运算符、和运算顺序。而根据逆波兰式的性质,运算符的先后顺序正好是从左往右的。故我们可以对存放题目的List进行遍历,发现首个运算符后,存储这个运算符,并取该运算符前的两个运算数进行比对,如果是重复的,则递归调用该方法,直到所有运算符都检查完毕。
五. 代码实现
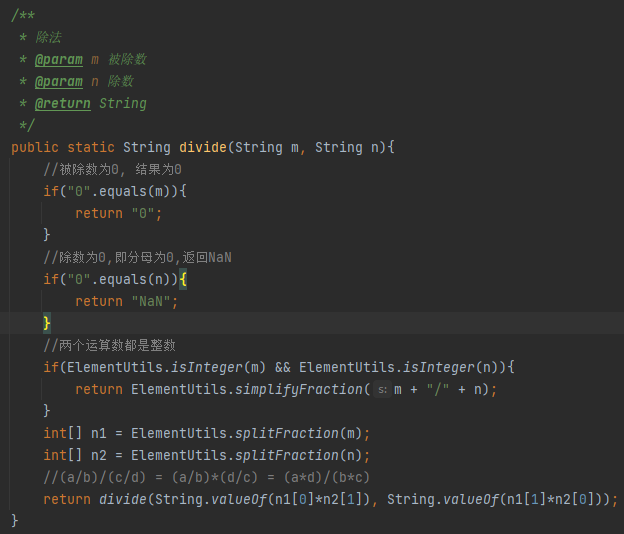
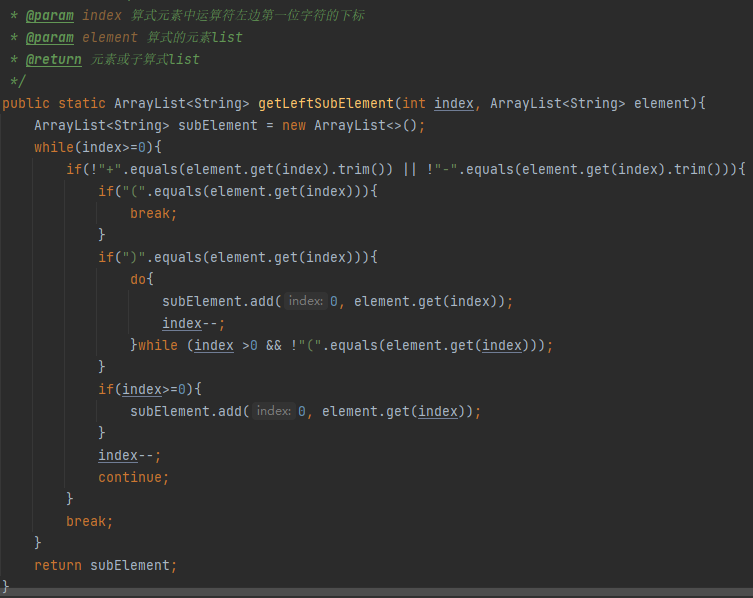
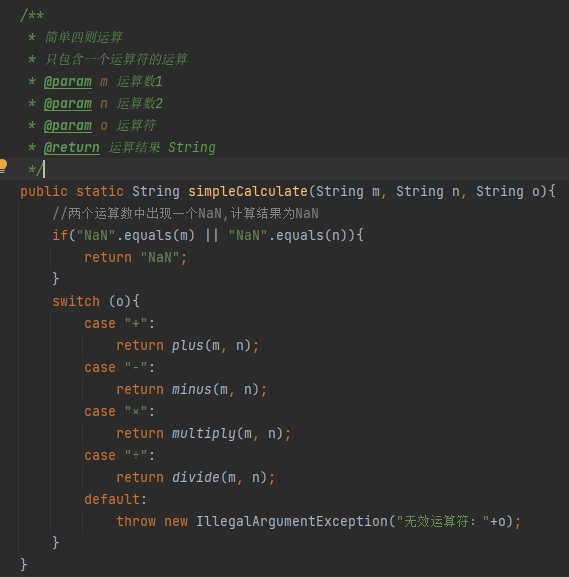
六. 运行实例和测试
生成一万道算式
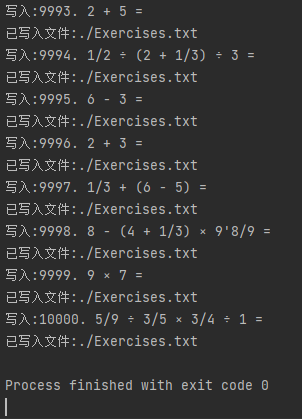
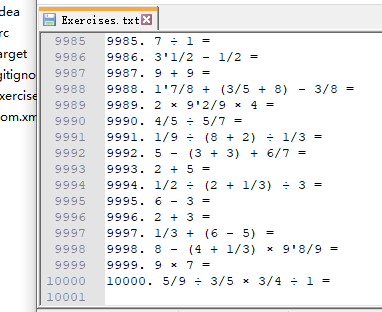
判断运算数是否为整数测试
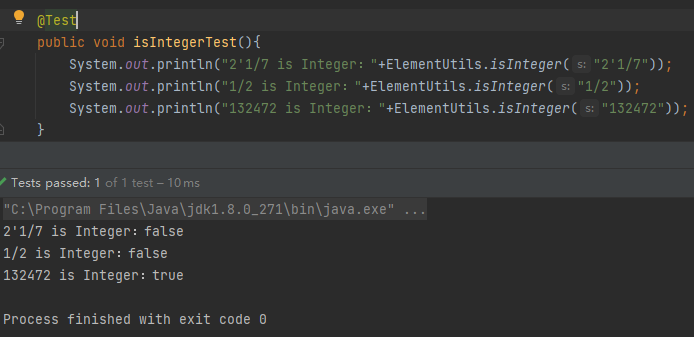
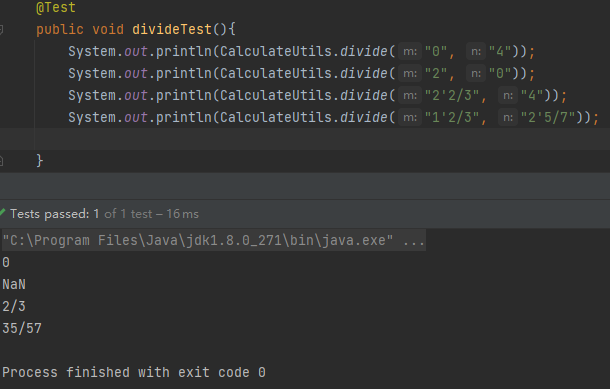
除法测试
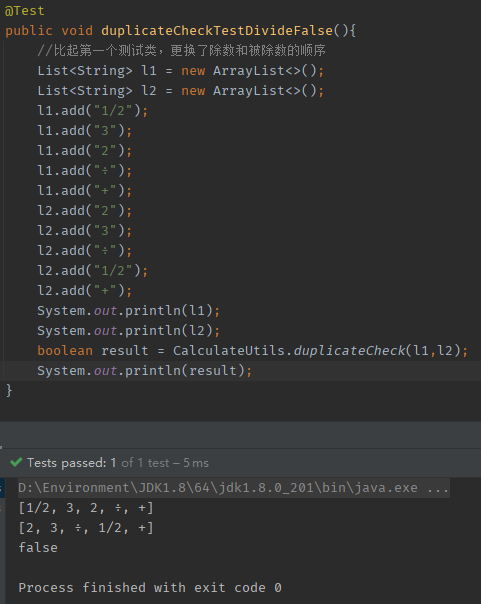
查重测试
七. 项目小结
陈卓鸿:通过本次合作编程,我了解到自己在开发上有很多不足,对git和github的使用还需要多加学习,尤其是最后的merge非常糟糕,而且在项目管理上还是会出现混乱,比如不同git版本之间的切换和复原。在本次和同学共同开发过程中,我深刻体会到编程中交流的重要性,有效率的交流会提高项目完成的速度。
张栩:首先这次结对作业是我为数不多的和同学合作开发的经历,比起平时独立思考的作业,合作开发更多的是需要我和搭档之间的配合与交流,比如这次作业中我和我的搭档首先商量好了大致的思路和数据结构,由我的搭档首先建立项目,而后我在GitHub上Fork之后进行一些方法的扩充,完善和测试。虽然在项目中遇到了比想象之中多得多的问题和异常,但因为合作开发,我们对对方的代码都有比较深入的了解,所以在探讨交流下都一一解决了,我认为结对编程对于开发效率的提高还是十分有帮助的。




