机器学习实战笔记（决策树）

 决策树

  决策树(decision tree)是一种基本的分类与回归方法。在分类问题中，表示基于特征对实例进行分类的过程，它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。决策树学习的经典算法：ID3，C4.5，CART

决策树的概念很简单，下图所示的流程图是一个简单的决策树 

 
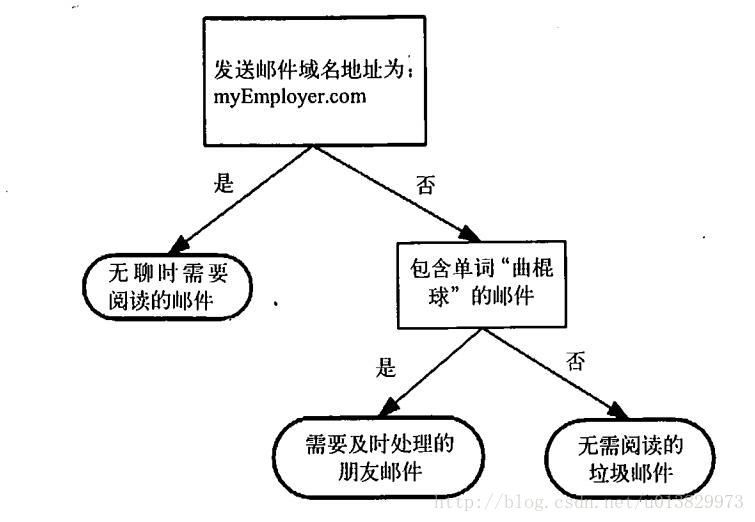
图1.1 流程图

其中，长方形代表判断模块(decision block)，椭圆形成代表终止模块(terminating block)，表示已经得出结论，可以终止运行。从判断模块引出的左右箭头称作为分支(branch)，它可以达到另一个判断模块或者终止模块。用专业的术语讲，分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型：内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性，叶结点表示一个类。图中的决策树，长方形和椭圆形都是结点。长方形的结点属于内部结点，椭圆形的结点属于叶结点，从结点引出的左右箭头就是有向边。而最上面的结点就是决策树的根结点(root node)。

 

  用决策树分类时，从根节点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子节点；这时每一个子节点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶节点。最后将实例分到叶节点的类中。

使用决策树的一般流程：

• 收集数据：可以使用任何方法。
• 准备数据：对收集完的数据进行整理，注意：树构造算法只适用于标称型数据，因此数值型数据必须离散化。
• 分析数据：可以使用任何方法，决策树构造完成之后，我们可以检查决策树图形是否符合预期。
• 训练算法：这个过程也就是构造决策树，同样也可以说是决策树学习，就是构造一个决策树的数据结构。
• 测试算法：使用经验树计算错误率。
• 使用算法：此步骤可以使用适用于任何监督学习算法，而使用决策树可以更好地理解数据的内在含义。

信息增益的理解

1948年，香农提出了 ”信息熵(entropy)“的概念，一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情，或者是我们一无所知的事情，需要了解大量信息==>信息量的度量就等于不确定性的多少。

例子：猜世界杯冠军，假如一无所知，猜多少次？每个队夺冠的几率不是相等的，比特(bit)来衡量信息的多少。

采用如下方式求信息熵：

1 当每个球队夺冠概率相等时候，32支参加世界杯夺冠球队的信息熵是5，计算是2^5=32，也就是你5次可以猜对那支球队夺冠。

2 当球队夺冠概率不相等，比如巴西、德国、荷兰是强队概率较大，信息熵就小于5，也就是你用不到5次就可以猜出哪个球队夺冠。

注：变量的不确定性越大，熵也就越大

决策树归纳算法 （ID3）

1970-1980， J.Ross. Quinlan首先提出ID3算法，第一步是选择属性判断结点，我们采用信息熵的比较。第二步是信息获取量(Information Gain)：Gain(A) = Info(D) - Infor_A(D)通过A来作为节点分类获取了多少信息

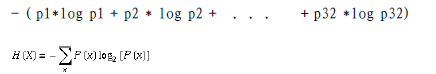
详解：

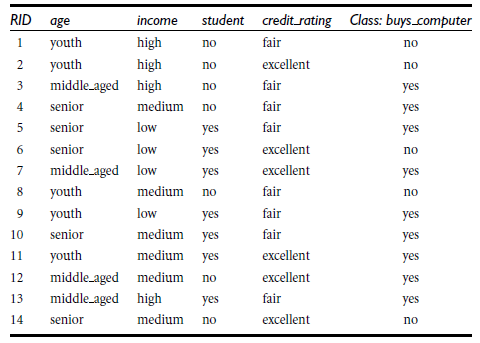
信息获取量/信息增益(Information Gain)：Gain(A) = Info(D) - Infor_A(D)，例如age的信息增益，Gain(age) = Info(buys_computer) - Infor_age(buys_computer)。

Info(buys_computer)是这14个记录中，购买的概率9/14，不购买的5/14，带入到信息熵公式。

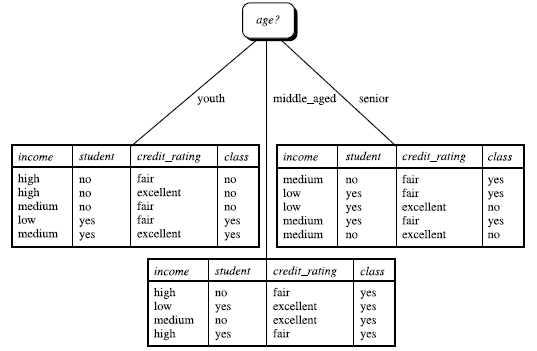
Infor_age(buys_computer)是age属性中，青年5/14购买概率是2/5,不购买3/5;中年4/14购买概率是1,不购买概率是0,老年5/14购买概率3/5，不购买概率是2/5.分别代入信息熵公式

Info(buys_computer)与Infor_age(buys_computer)做差，即是age的信息增益，具体如下：

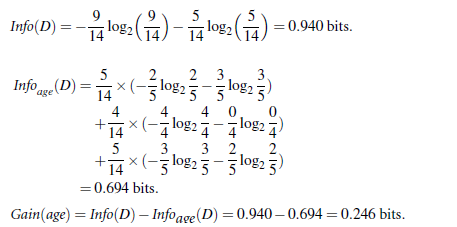
类似，Gain(income) = 0.029, Gain(student) = 0.151, Gain(credit_rating)=0.048

所以，选择信息增益最大的作为根节点即age作为第一个根节点

 

重复计算即可

2.4 决策树算法：

决策树算法的形式化描述如下：

• 树以代表训练样本的单个结点开始（步骤1）。
• 如果样本都在同一个类，则该结点成为树叶，并用该类标号（步骤2 和3）。
• 否则，算法使用称为信息增益的基于熵的度量作为启发信息，选择能够最好地将样本分类的属性（步骤6）。该属性成为该结点的“测试”或“判定”属性（步骤7）。在算法的该版本中，
• 所有的属性都是分类的，即离散值。连续属性必须离散化。
• 对测试属性的每个已知的值，创建一个分枝，并据此划分样本（步骤8-10）。
• 算法使用同样的过程，递归地形成每个划分上的样本判定树。一旦一个属性出现在一个结点上，就不必该结点的任何后代上考虑它（步骤13）。
• 递归划分步骤仅当下列条件之一成立停止：
• (a) 给定结点的所有样本属于同一类（步骤2 和3）。
• (b) 没有剩余属性可以用来进一步划分样本（步骤4）。在此情况下，使用多数表决（步骤5）。
• 这涉及将给定的结点转换成树叶，并用样本中的多数所在的类标记它。替换地，可以存放结
• 点样本的类分布。
• (c) 分枝
• test_attribute = a i 没有样本（步骤11）。在这种情况下，以 samples 中的多数类
• 创建一个树叶（步骤12）

在决策树ID3基础上，又进行了算法改进，衍生出 其他算法如：C4.5: （Quinlan） 和Classification and Regression Trees (CART): (L. Breiman, J. Friedman, R. Olshen, C. Stone)。这些算法

共同点：都是贪心算法，自上而下(Top-down approach)

 

区别：属性选择度量方法不同： C4.5 （gain ratio，增益比), CART(gini index，基尼指数), ID3 (Information Gain，信息增益)

 

 

 如何处理连续性变量的属性？ 
 

 

 有些数据是连续性的，其不像如上实验数据可以离散化表示。诸如根据天气情况预测打球案例中，其湿度是一个连续值，我们的做法是将湿度70作为一个分界点，这里就是连续变量离散化的体现。
 

补充知识

 

树剪枝叶 （避免overfitting)：为了避免拟合问题，我们可以对归于繁琐的树进行剪枝（就是降低树的高度），可以分为先剪枝和后剪枝。

决策树的优点：直观，便于理解，小规模数据集有效     

决策树的缺点：处理连续变量不好、类别较多时，错误增加的比较快、可规模性一般

总结

1、 决策树的优点：

• 数据形式易于理解。
• 计算复杂度不高，对中间值的确实不敏感，可以处理不相关特征数据。
• 需要准备的数据量不大，而其他的技术往往需要很大的数据集，需要创建虚拟变量，去除不完整的数据，但是该算法对于丢失的数据不能进行准确的预测。
• 决策树算法的时间复杂度(即预测数据)是用于训练决策树的数据点的对数
• 可以同时处理数值变量和分类变量。其他方法大都适用于分析一种变量的集合。
• 可以处理多值输出变量问题。
• 使用白盒模型。如果一个情况被观察到，使用逻辑判断容易表示这种规则。相反，如果是黑盒模型（例如人工神经网络），结果会非常难解释。
• 即使对真实模型来说，假设无效的情况下，也可以较好的适用。

2、 决策树的缺点：

• 决策树算法学习者可以创建复杂的树，但是没有推广依据，这就是所谓的过拟合，为了避免这种问题，出现了剪枝的概念，即设置一个叶子结点所需要的最小数目或者设置树的最大深度
• 决策树的结果可能是不稳定的，因为在数据中一个很小的变化可能导致生成一个完全不同的树，这个问题可以通过使用集成决策树来解决
• 众所周知，学习一个最优决策树是NP-完全问题。因此，实际决策树学习算法是基于启发式算法，如贪婪算法，寻求在每个节点上的局部最优决策。这样的算法不能保证返回全局最优决策树。对样本和特征的随机抽样可以防止整体效果偏差。
• 概念难以学习，因为决策树没有很好的解释他们，例如，XOR。
• 分类任务时，不能解决类别不平衡问题。

 

 

参考博客：http://www.cnblogs.com/onemorepoint/p/8310898.html