多项式曲线拟合

多项式曲线拟合

本文参照PRML第一章与第三章，实作验证了多项式曲线拟合的例子

线性基函数模型

现在假设一个训练集，这个训练集由\(\mathbf x\)的\(N\)的观测组成，写作\(\mathbf x = (x_1, \ldots, x_N)^\top\)，与之对应的\(\mathbf t\)的观测值记作\(\mathbf t = (t_1, \ldots, t_N)^\top\)。现在，从\([0,1]\)之间均匀选取\(N\)个\(x_n\)，目标数据\(\mathbf t\)的获取方式是：首先计算函数\(\sin(2\pi x)\)的对应值，然后给得到的每个数据点增加一个小的满足高斯分布的随机噪声，从而得到对应的\(t_n\)值，即

\[ t_n = \sin(2\pi x_n) + \varepsilon \]

其中\(\varepsilon\)采样自\(\mathcal N(\varepsilon\ |\ 0, \sigma^2)\)。

我们的目标是利用这个训练集预测对于新的输入变量\(x\)的目标变量值\(t\)。这本质上是一个困难的问题，因为我们不得不从有限的数据生成对应的模型。而且，观测到的数据被噪声干扰，因此对于一个给定的\(x\)，合适的\(t\)值具有不确定性。但是现在，我们可以使用一种不太正式的，相当简单的方式来进行曲线的拟合。我们考虑如下的线性模型

\[ y(\mathbf x, \mathbf \omega) = \omega_0 + \sum_{j=1}^{M-1}\omega_j\phi_j(\mathbf x) \]

其中\(\phi_j(\mathbf x)\)被称为基函数，且这个模型中的参数总数为\(M\)。

在本例中，基函数\(\phi_j(\mathbf x)\)设为

\[ \phi_j(\mathbf x) = x^j \]

如果我们设定\(\phi_0(\mathbf x)=1\)，则可将上式模型写作

\[ y(\mathbf x, \mathbf \omega) = \sum_{j=0}^{M-1}\omega_j\phi_j(\mathbf x) = \mathbf \omega^\top\phi(\mathbf x) \]

其中\(\mathbf \omega=(\omega_0, \ldots, \omega_{M-1})^\top\)且\(\mathbf\phi=(\phi_0, \ldots, \phi_{M-1})^\top\)

我们可以使用非线性的基函数，使得\(y(\mathbf x, \mathbf\omega)\)为输入向量\(\mathbf x\)的一个非线性函数，但是这样的情况依然被称作是线性函数，因为这个函数是\(\mathbf \omega\)的线性函数。

模型的参数估计

最小平方误差估计

系数\(\mathbf \omega\)的估计可以通过最小化误差函数来获得。一个简单的广泛应用的误差函数是每个数据点\(x_n\)的预测值\(y(x_n, \mathbf\omega)\)与目标值\(t_n\)相差的平方和

\[\mathbf E(\omega)=\frac{1}{2}\sum_{n=1}^N\left\{ y(x_n, \mathbf\omega) - t_n \right\}^2 \]

其中，\(\frac{1}{2}\)是为了计算方便。现在我们要选取使得\(\mathbf E(\mathbf\omega)\) 最小的 \(\mathbf\omega\)值，因为，若所有数据均预测正确，那么误差值就为零。即

\[ \mathbf\omega^* = \arg\min_{\mathbf\omega}\mathbf E(\mathbf\omega) \]

由于误差函数是\(\mathbf\omega\)的二次函数，所以关于\(\mathbf\omega\)的导数是线性函数，令其等于零，只有一解，也即误差函数的最小值有一个唯一解。

现在将上一节所述模型代入误差函数求解，即

\[ \mathbf E(\mathbf\omega)=\frac{1}{2}\sum_{n=1}^N\left\{ t_n-\omega^\top\mathbf\phi(x_n) \right\}^2 \]

对其关于\(\mathbf\omega\)求导， 得

\[ \nabla_{\mathbf\omega}\mathbf E(\mathbf\omega) = \sum_{n=1}^N\left\{ t_n-\mathbf\omega^\top\mathbf\phi(x_n) \right\}\mathbf\phi(x_n)^\top \]

令其等于零，可得

\[ 0 = \sum_{n=1}^{N}t_n\mathbf\phi(x_n)^\top - \mathbf\omega^\top\left( \sum_{n=1}^{N}\mathbf\phi(x_n)\phi(x_n)^\top \right) \]

求解\(\mathbf\omega\)，有

\[\mathbf\omega^* = (\mathbf\Phi^\top\mathbf\Phi)^{-1}\mathbf\Phi^\top\mathbf t \]

这里\(\mathbf\Phi\)是一个\(N\times M\)的矩阵，其元素\(\Phi_{nj} = \phi_j(x_n)\)，即

\[\mathbf\Phi = \left( \begin{matrix} \phi_0(x_1) & \phi_1(x_1) &\cdots & \phi_{M-1}(x_1) \\ \phi_0(x_2) & \phi_1(x_2) &\cdots & \phi_{M-1}(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_0(x_N) & \phi_1(x_N) &\cdots & \phi_{M-1}(x_N) \\ \end{matrix} \right) \]

式中

\[ (\mathbf\Phi^\top\mathbf\Phi)^{-1}\mathbf\Phi^\top \]

被定义为\(\mathbf\Phi\)的MP伪逆。

之后预测模型可以写作

\[y(\mathbf x, \mathbf \omega) = \mathbf \omega^{*\top}\phi(\mathbf x) \]

最大似然估计

最小平方误差的解可以看成高斯噪声模型假设下的最大似然解。

与一开始一样，假设目标变量\(t\)由确定的函数\(y(\mathbf x, \mathbf\omega)\)给出，这个函数被附加了一个高斯噪声，即

\[ t = \sin(2\pi x) + \varepsilon \]

其中\(\varepsilon\)是一个零均值，精度(方差的倒数)为\(\beta=\frac{1}{\sigma^2}\)的高斯随机变量。因此，有

\[ p(t\ |\ x, \omega, \beta) = \mathcal N(t\ |\ y(\mathbf x, \mathbf\omega), \beta^{-1}) \]

考虑现在有给定的输入数据集\(\mathbf X = \{x_1, \ldots, x_N\}\)，对应的目标值为\(\mathbf t = \{t_1, \ldots, t_N\}\)。那么观测数据的似然函数为

\[ p(\mathbf t\ |\ \mathbf X, \mathbf \omega, \beta) = \prod_{n=1}^N\mathcal N(t_n\ |\ \mathbf\omega^\top\mathbf\phi(x_n), \beta^{-1}) \]

取对数，并且使用一元高斯分布的标准形式，有

\[ \begin{align} \log p(\mathbf t\ |\ \mathbf\omega, \beta^{-1}) &= \sum_{n=1}^{N}\log\mathcal N(t_n\ |\ \mathbf\omega^\top\mathbf\phi(x_n), \beta^{-1}) \notag \\ &= \frac{N}{2}\log\beta - \frac{N}{2}\log(2\pi)-\beta E_D(\mathbf \omega) \end{align} \]

其中平方和误差函数被定义为

\[ E_D(\mathbf \omega) = \frac{1}{2}\sum_{n=1}^{N}\{t_n-\mathbf\omega^\top\mathbf\phi(x_n) \}^2 \]

写出了似然函数，我们可以使用最大似然函数的方法确定\(\mathbf \omega\)。

在这里，关于\(\mathbf\omega\)求最大值，与之前求最小平方误差等价。求解\(\mathbf\omega\)有

\[\mathbf\omega_{\mathrm ML} = (\mathbf\Phi^\top\mathbf\Phi)^{-1}\mathbf\Phi^\top\mathbf t \]

正则化

可以通过给误差函数添加正则化项来控制过拟合，因此需要最小化的误差函数为

\[ \mathbf E(\mathbf\omega) +\lambda \mathbf E_\omega(\mathbf\omega) \]

其中\(\lambda\)是正则化系数。正则化项一个简单的形式是\(\ell_2\)正则

\[\mathbf E_\omega(\omega) = \frac{1}{2}\mathbf\omega^\top\mathbf\omega \]

考虑\(\ell_2\)正则化，那么整个误差函数就变为

\[\frac{1}{2}\sum_{n=1}^N\left\{ t_n-\mathbf\omega^\top \mathbf\phi(x_n) \right\}^2+\frac{\lambda}{2}\mathbf\omega^\top\mathbf\omega \]

令其关于\(\mathbf\omega\)的导数等于零，可得

\[\mathbf\omega = (\lambda\mathbf I+\mathbf\Phi^\top\mathbf\Phi)^{-1}\mathbf\Phi^\top\mathbf t \]

实验

使用 Python 模拟实验。

导入必要的数据包

import matplotlib.pyplot as plt 
import numpy as np 
from numpy.linalg import inv
from functools import partial

生成具有高斯噪声的目标数据值\(t_n\)

RANGE = [0, 1]
X = np.linspace(*RANGE, 10)
target = np.sin(2*np.pi*X) + np.random.normal(0, 0.2, len(X))

定义\(\phi(x_n)\)与\(\mathbf\Phi\)

def phi(x, m):
    _phi = [ 1 ]
    for i in range(m):
        _phi.append(x**(i+1))
    return _phi

def Phi(X, m):
    _Phi = [ ]
    for x in X:
        _Phi.append(phi(x, m))
    return np.array(_Phi)

定义预测函数，以及预测模型的绘制函数

def predict(x, omega):
    return  omega.dot(phi(x, len(omega)-1))
    
def plot_predict(func, range, label='', resolution=0.02, color='red'):
    _x = np.arange(range[0], range[1], resolution)
    _y = [ func(x) for x in _x ]
    plt.plot(_x, _y, color=color, label=label)

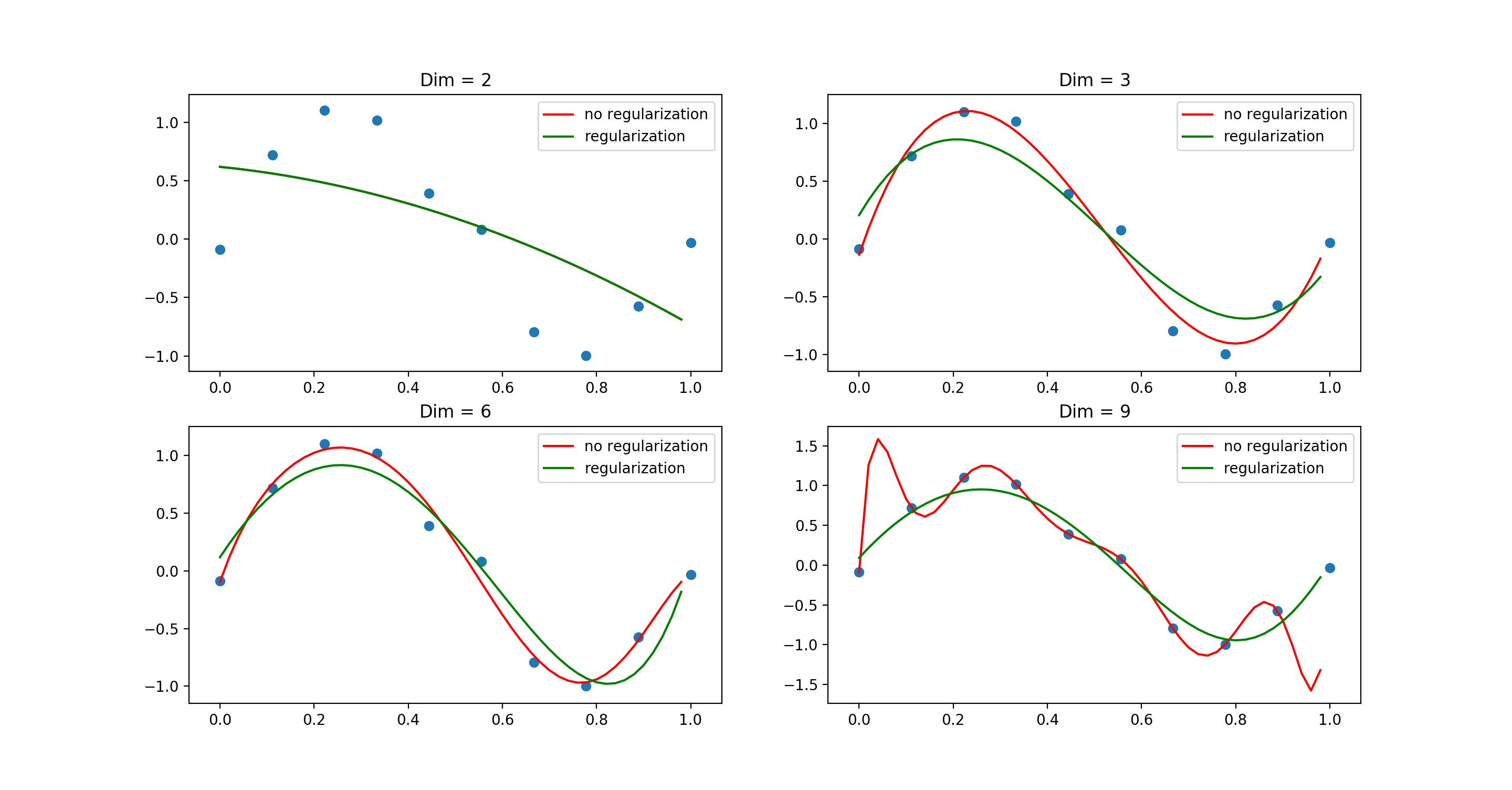
对比各种参数个数的模型，以及正则化模型之间的对比

for idx, dim in enumerate([2, 3, 6, 9]):
    # 计算模型参数
    _Phi = Phi(X, dim)
    omega = inv(_Phi.T.dot(_Phi)).dot(_Phi.T).dot(target)
    ## 正则化
    lambda_ = 1e-3
    omega_r = inv(lambda_*np.eye(dim+1) + _Phi.T.dot(_Phi)).dot(_Phi.T).dot(target)

    # 预测函数
    predict = partial(predict, omega=omega)
    predict_r = partial(predict, omega=omega_r)

    # 绘制图像
    ax = plt.subplot(2, 2, idx+1)
    plot_predict(predict, RANGE, label='no regularization', color='red')
    plot_predict(predict_r, RANGE, label='regularization', color='green')
    plt.scatter(X, target)
    plt.title('Dim = $%d$' % dim)
    plt.legend()
    
plt.show()

实验结果