Networkx算法Cuts

来自官方文档Networkx Reference Release2.4

1、boundary_expansion(G,S)

返回值：切割边数/S子集节点数

G = nx.barbell_graph(4,0) #生成杠铃图
S ={0,1,2,3,4}
X=nx.boundary_expansion(G,S)
print(X)

2、conductance(G,S,T)

返回：切割边数/两个子集最小的volume。volume是子集所有节点度的总和。

例如S={0,1,2},T={3,4,5,6,7} 。切割边数为3，S子集的度数和volume为9，T子集度数和volume为17。返回值为1/3

    G = nx.barbell_graph(4,0)
    S ={0,1,2}
    T ={3,4,5,6,7}
    X=nx.conductance(G,S,T)
    print(X)

3、volume（G，T）

返回：子集T所有节点度的总和。

    G = nx.barbell_graph(4,0)
    S ={0,1,2}
    X=nx.volume(G,S)
    print(X)

4、cut_site(G,S,T)

返回：S、T两个子集之间的边的权值之和

    G = nx.barbell_graph(4,0)
    S ={0,1,2,3}
    T ={4,5,6,7}
    X=nx.cut_size(G,S,T)
    print(X)

5、edge_expansion(G,S,T=None,weight=None)

返回：割边数与两个子集最小的基数（节点数）的商。以下割边为4，len（S）=2，因此返回值为2.0

    G = nx.barbell_graph(4,0)
    S ={0,1}
    T ={2,3,4,5,6,7}
    X=nx.edge_expansion(G,S,T)
    print(X)

6、mixing_expansion(G, S, T=None, weight=None)

返回：mixing expansion是割边数与两倍图的边数的商。以下割边数为3，barbell_graph(4,0)的边为13。因此返回值为3/（2*13）=0.11538461538461538461538461538462

    G = nx.barbell_graph(4,0)
    S ={0,1,2}
    T ={3,4,5,6,7}
    X=nx.mixing_expansion(G,S,T)
    print(X)

7、node_expansion(G, S)

官方对node_boundary的定义是：

The node boundary is all nodes in the edge boundary of a given
set of nodes that are in the set.

翻译：节点边界是给定边界上的所有节点集合中节点的集合。

node_expansion返回值：node_boundary 与 子集基数之商。例如S={0,1,2},则node_boundary为节点0、1、2、3、4、5、6、7。所以返回8/5=1.6

    G = nx.barbell_graph(4,0)
    S ={0,1,2,3,4}
    X=nx.node_expansion(G,S)
    print(X)

8、normalized_cut_size(G, S, T=None, weight=None ）

返回：割边数乘以S、T子集总度数倒数之和。cuts*(1/T_volume + 1/S_volume)

    G = nx.barbell_graph(4,0)
    S ={0,1,2}
    X=nx.normalized_cut_size(G,S)
    print(X)

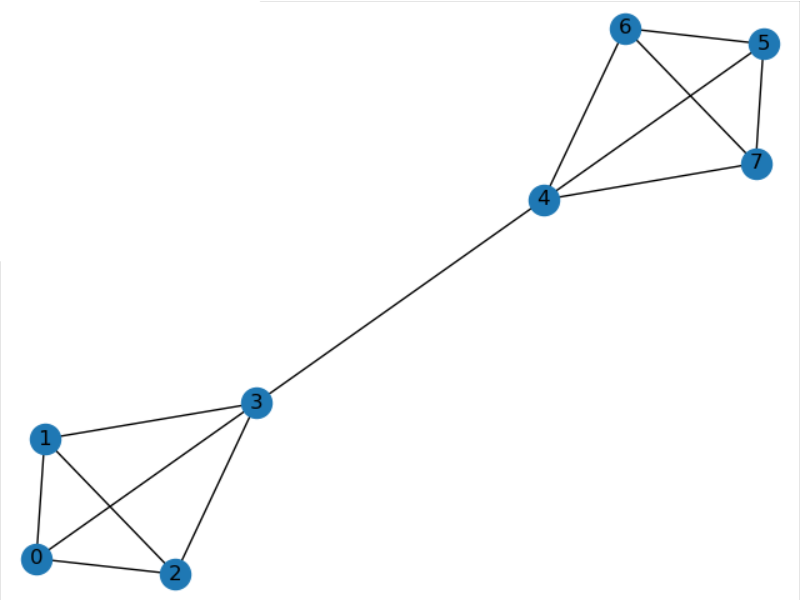
附图 barbell_graph(4,0) 杠铃图