排序算法学习笔记(三)-- 快速排序
快速排序 Quick Sort
1. 算法过程
快速排序(Quick Sort)使用分治法策略。
它的基本思想是:选择一个基准数,通过一趟排序将要排序的数据分割成独立的两部分;其中一部分的所有数据都比另外一部分的所有数据都要小。然后,再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序流程:
(1) 从数列中挑出一个基准值。
(2) 将所有比基准值小的摆放在基准前面,所有比基准值大的摆在基准的后面(相同的数可以到任一边);在这个分区退出之后,该基准就处于数列的中间位置。
(3) 递归地把"基准值前面的子数列"和"基准值后面的子数列"进行排序。
上述文字来源: https://www.cnblogs.com/skywang12345/p/3596746.html
推荐帮助理解的文章: https://wiki.jikexueyuan.com/project/easy-learn-algorithm/fast-sort.html
2.可视化展示

图源:https://timewentby.com/language/java/543.html
3. 代码实现
python版本:
1 # 对nums[l...r]部分进行partition操作 2 # 返回j, 使得nums[l...j-1] < arr[j] ; nums[j+1...r] > arr[j] 3 def __partition(nums, left, right): 4 refer = nums[left] # 参照数值,这里取传入的最左边部分 5 6 j = left 7 for i in range(left + 1, right + 1): 8 if nums[i] < refer: 9 nums[j + 1], nums[i] = nums[i], nums[j + 1] 10 j += 1 11 nums[left], nums[j] = nums[j], nums[left] 12 13 return j 14 15 16 def __quick_sort(nums, left, right): 17 if left >= right: 18 return 19 20 p = __partition(nums, left, right) 21 __quick_sort(nums, left, p) 22 __quick_sort(nums, p + 1, right) 23 24 25 def quick_sort(nums): 26 __quick_sort(nums, 0, len(nums) - 1)
C++版本:
1 // 对arr[l...r]部分进行partition操作 2 template<typename T> 3 int __partition(T arr[],int l, int r) { 4 5 T refer = arr[l]; 6 7 int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v 8 for (int i = l + 1; i <= r; i++) { 9 if (arr[i] < refer) 10 swap(arr[++j], arr[i]); 11 } 12 swap(arr[l], arr[j]); 13 14 return j; 15 } 16 17 // 对arr[l...r]部分进行快速排序 18 template<typename T> 19 void __quickSort(T arr[], int l, int r) { 20 21 if (l >= r) 22 return; 23 24 int p = __partition(arr, l, r); 25 __quickSort(arr, l, p); 26 __quickSort(arr, p + 1, r); 27 } 28 29 template<typename T> 30 void quickSort(T arr[], int n) { 31 32 __quickSort(arr, 0, n - 1); 33 }
4. 算法优化
类似于归并排序,快速排序也是将整个数组一分为二(小于标定点的部分和大于标定点的部分),整个过程也会行程一棵二叉树。但区别在于,归并排序的划分是均匀地一分为二,产生的二叉树高度近乎为logn。而上面实现的快速排序有在顺序性较强的时候,划分的两个部分是极度偏斜的,就会产生平衡性很差的树。最差的情况会退化成O(n2)级别的算法。(形成的二叉树退化成了链表)
改进方式:在partition操作之前先随机选择一个元素与最左边元素交换。 也可以再加入对小规模数组进行插入排序的优化。
C++ 实现:
// 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot swap( arr[l] , arr[rand()%(r-l+1)+l] );
5. 双路快速排序
上述的实现方法是默认把等于标定元素的值都放在了右半部分。如果等于标定元素的数值过多,即数组中存在大量的重复元素时,此时partition的划分仍会十分偏斜,再次退化。
双路快排的过程:

图源:https://segmentfault.com/a/1190000021726667
python版本:
1 def insertion_sort(nums, left, right): 2 for i in range(left + 1, right + 1): 3 pre = i - 1 4 cur_num = nums[i] 5 while pre >= left and nums[pre] > cur_num: 6 nums[pre + 1] = nums[pre] 7 pre -= 1 8 nums[pre + 1] = cur_num 9 10 11 # 双路快速排序的partition 12 # 返回j, 使得arr[l...j-1] < arr[j] ; arr[j+1...r] > arr[j] 13 def __partition_two_way(nums, left, right): 14 # 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot 15 rand_index = random.randint(left, right) 16 nums[left], nums[rand_index] = nums[rand_index], nums[left] 17 refer = nums[left] 18 19 i, j = left + 1, right 20 """ 21 注意这里的边界:用小于和大于号,遇到大量相等的partition元素的时候, 22 15 程序可以通过i++,j++使得树的分裂点更居中,因此树也更趋于平衡 23 16 而用小于等于和大于等于方式则会将连续出现的这些值归为其中一方,使得两棵子树不平衡 24 """ 25 while True: 26 while i <= right and nums[i] < refer: 27 i += 1 28 while j >= left + 1 and nums[j] > refer: 29 j -= 1 30 if i > j: 31 break 32 nums[i], nums[j] = nums[j], nums[i] 33 i += 1 34 j -= 1 35 nums[left], nums[j] = nums[j], nums[left] 36 return j 37 38 39 def __quick_sort(nums, left, right): 40 if right - left <= 15: # 当数据规模很小的时候采用插入排序 41 insertion_sort(nums, left, right) 42 return 43 44 p = __partition_two_way(nums, left, right) 45 __quick_sort(nums, left, p) 46 __quick_sort(nums, p + 1, right) 47 48 49 def quick_sort(nums): 50 __quick_sort(nums, 0, len(nums) - 1)
C++版本:
1 // 双路快速排序的partition 2 // 返回j, 使得arr[l...j-1] < arr[j] ; arr[j+1...r] > arr[j] 3 template<typename T> 4 void __partitionTwoWay(T arr[], int l, int r) { 5 6 // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot 7 swap(arr[l], arr[rand() % (r - l + 1) + l]); 8 T refer = arr[l]; 9 10 // arr[l+1...i) <= v; arr(j...r] >= v 11 int i = l + 1, j = r; 12 while (true) 13 { 14 // 注意这里的边界:用小于和大于号,遇到大量相等的partition元素的时候, 15 // 程序可以通过i++,j++使得树的分裂点更居中,因此树也更趋于平衡 16 // 而用小于等于和大于等于方式则会将连续出现的这些值归为其中一方,使得两棵子树不平衡 17 while (i<=r && arr[i] < refer) i++; 18 while (j >= l && arr[j] > refer) j--; 19 if (i > j) break; 20 swap(arr[i], arr[j]); 21 i++; 22 j--; 23 } 24 25 swap(arr[l], arr[j]); 26 return j; 27 } 28 29 // 对arr[l...r]部分进行快速排序 30 template <typename T> 31 void _quickSort(T arr[], int l, int r) { 32 33 // 对于小规模数组, 使用插入排序进行优化 34 if (r - l <= 15) { 35 insertionSort(arr, l, r); 36 return; 37 } 38 39 int p = _partitionTwoWay(arr, l, r); 40 _quickSort(arr, l, p - 1); 41 _quickSort(arr, p + 1, r); 42 } 43 44 template <typename T> 45 void quickSort(T arr[], int n) { 46 47 srand(time(NULL)); 48 _quickSort(arr, 0, n - 1); 49 } 50 51 // 对arr[l...r]范围的数组进行插入排序 52 template<typename T> 53 void insertionSort(T arr[], int l, int r) { 54 55 for (int i = l + 1; i <= r; i++) { 56 57 T e = arr[i]; 58 int j; 59 for (j = i; j > l && arr[j - 1] > e; j--) 60 arr[j] = arr[j - 1]; 61 arr[j] = e; 62 } 63 64 return; 65 }
6 三路快速排序
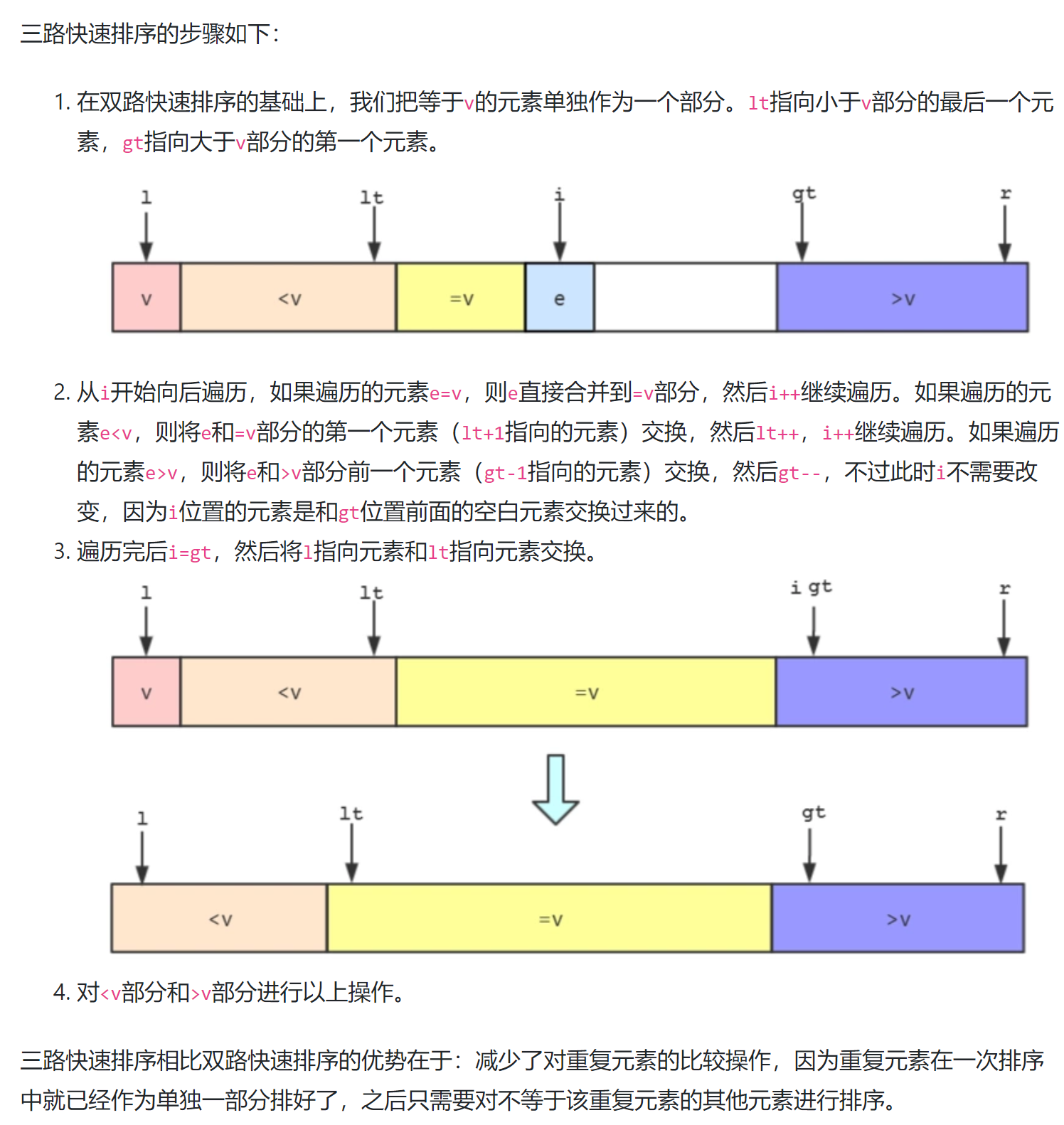
图源:https://segmentfault.com/a/1190000021726667
python版本:
1 def __partition_three_ways(nums, left, right): 2 # 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot 3 rand_index = random.randint(left, right) 4 nums[left], nums[rand_index] = nums[rand_index], nums[left] 5 refer = nums[left] 6 7 less_than, great_than = left, right + 1 8 i = left 9 while i < great_than: 10 if nums[i] < refer: 11 nums[i], nums[less_than + 1] = nums[less_than + 1], nums[i] 12 i += 1 13 less_than += 1 14 elif nums[i] > refer: 15 nums[i], nums[great_than - 1] = nums[great_than - 1], nums[i] 16 great_than -= 1 17 else: 18 i += 1 19 nums[left], nums[less_than] = nums[less_than], nums[left] 20 21 return less_than, great_than 22 23 24 def __quick_sort(nums, left, right): 25 if right - left <= 15: # 当数据规模很小的时候采用插入排序, 具体过程在上面 26 insertion_sort(nums, left, right) 27 return 28 29 lt, gt = __partition_three_ways(nums, left, right) 30 __quick_sort(nums, left, lt - 1) 31 __quick_sort(nums, gt, right) 32 33 34 def quick_sort(nums): 35 __quick_sort(nums, 0, len(nums) - 1)
C++版本:
1 template<typename T> 2 void __quickSort3Ways(T arr[], int l, int r) { 3 // 对于小规模数组, 使用插入排序进行优化, 具体过程在上面实现中有 4 if (r - l <= 15) { 5 insertionSort(arr, l, r); 6 return; 7 } 8 9 // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot 10 swap(arr[l], arr[rand() % (r - l + 1) + l]); 11 12 T refer = arr[l]; 13 14 int lt = l; // arr[l+1...lt] < refer 15 int gt = r + 1; // arr[gt...r] > refer 16 int i = l + 1; // arr[lt+1...i) == refer 17 while (i < gt) { 18 if (arr[i] < refer) { 19 swap(arr[i], arr[lt + 1]); 20 i++; 21 lt++; 22 } 23 else if (arr[i] > refer) { 24 swap(arr[i], arr[gt - 1]); 25 gt--; 26 } 27 else { // arr[i] == refer 28 i++; 29 } 30 } 31 32 swap(arr[l], arr[lt]); 33 34 __quickSort3Ways(arr, l, lt - 1); 35 __quickSort3Ways(arr, gt, r); 36 37 } 38 39 template <typename T> 40 void quickSort3Ways(T arr[], int n) { 41 42 srand(time(NULL)); 43 __quickSort3Ways(arr, 0, n - 1); 44 }
7
- 时间复杂度:O(nlogn) (平均)
- 空间复杂度:O(1)
- 不稳定排序
- 原地排序
- 分治思想
8 用快速排序的思想解决topK问题
在lintcode的上刷过这道题,当时使用堆排序的思路进行解题。故晚些时候另设一篇博客来记录两种思路。



