排序算法学习笔记（一）-- 冒泡排序，选择排序，插入排序，希尔排序

写在前面：

 1.图片来源是从别的博客转来的，后期有空会自己使用java swing实现。

 2.代码实现由于个人习惯使用了C++和python，https://zhuanlan.zhihu.com/p/57088609博主实现了java版本。

 3.这里的代码实现排序顺序都是从左到右的升序。想要实现逆序可以直接颠倒数组。其实所谓的“小”只是相对的，“小”的规则可以通过重载运算符或者传入比较器，比较函数来实现自己想要的标准，来变成“大”

1.冒泡排序（bubble sort）

1.1 算法过程：

　　比方对于一个从左到右排列的数组。比较相邻的元素。如果左边比第右边大，就交换他们两个。对每一对相邻元素作同样的工作，从开始第一对到尾部的最后一对。这样尾部的元素将会是最大的元素。从左到右（除尾端的）每个元素依次作为起点重复上述的步骤。 

       算法名字很形象，每一个元素就是慢慢浮动到自己应该在的位置。借《啊哈！算法》中的一个图来理解

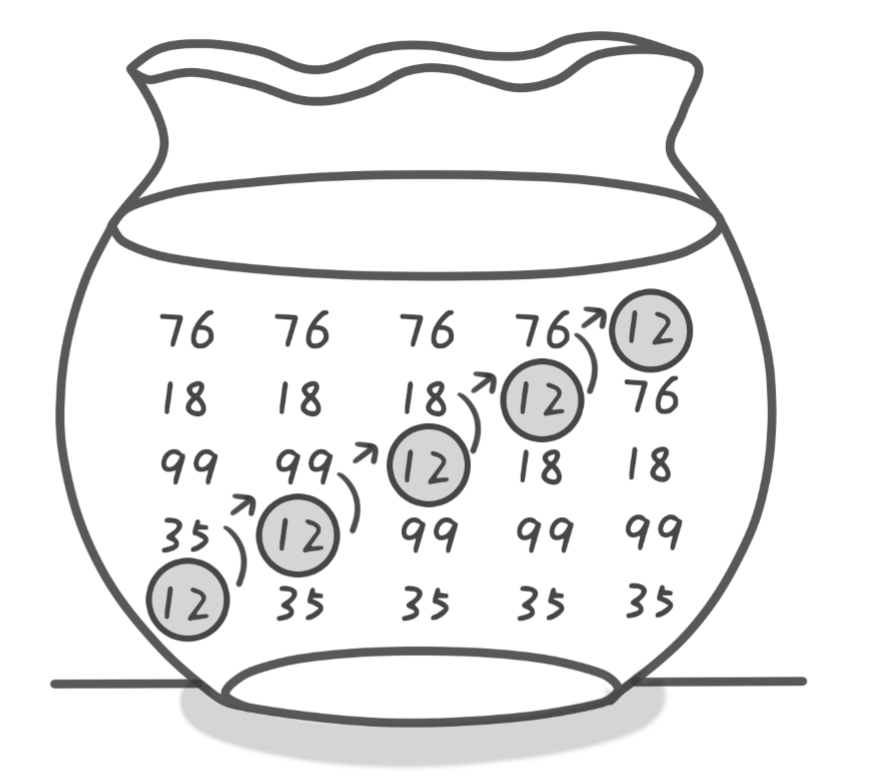
1.2 可视化展示：

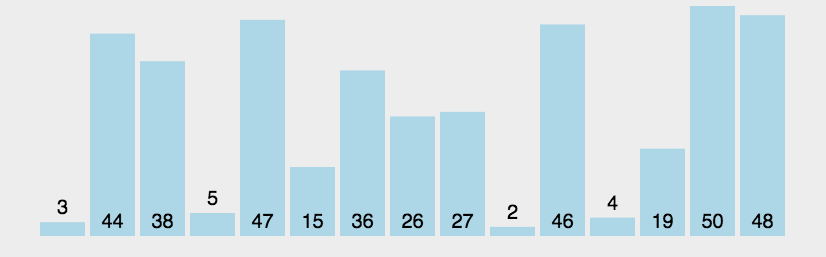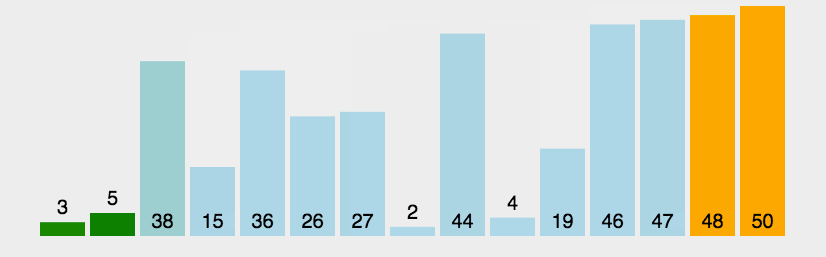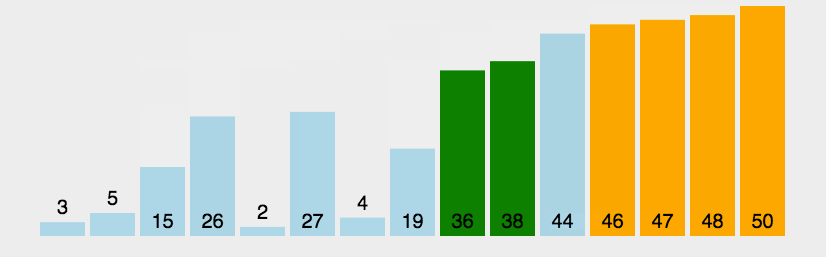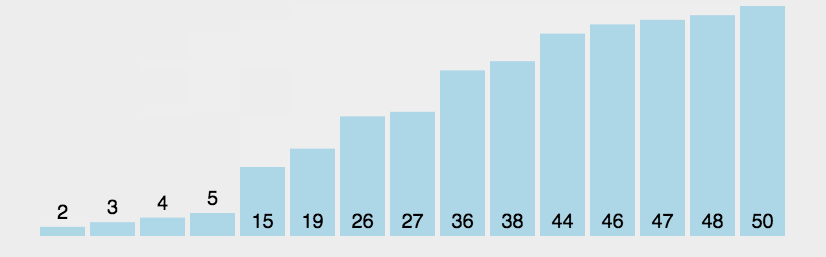
图源：https://juejin.im/post/5b4d8c47e51d4519105d4ec3

1.3 代码：

python版本：

def bubble_sort(nums):
    length = len(nums)
    if(length==0):
        return nums
    for i in range(length):
        for j in range(i,length):
            if nums[i]>nums[j]:
                nums[i],nums[j] = nums[j],nums[i]
    return nums

C++版本：

template<typename T> 
void bubbleSort(T arr[], int length) {
    for (int i = 0; i < length - 1; i++){
        for (int j = 0; j < length- 1 - i; j++)
            if (arr[j] > arr[j + 1])
                swap(arr[j], arr[j + 1]);
    }
}  

 

1.4 算法改进

　　优化1：设立一个“flag”，记录每一次遍历过程中是否发生了交换。若没有发生交换说明数组已经是有序的了，可以提前退出循环。

　　优化2：可以记录最后一次发生交换的位置，此位置之后的元素已经是有序的，不需要再进行遍历。

　　实现优化1（C++）：

template<typename T>
void bubbleSort( T arr[] , int length){

    bool swapped;

    do{
        swapped = false;
        for (int i = 0; i < length - 1; i++)
            for (int j = 0; j < length - 1 - i; j++)
                if (arr[j] > arr[j + 1]){
                    swap(arr[j], arr[j + 1]);
                    swapped=true;
        }

    }while(swapped);
}

　　实现优化2(C++)：

template<typename T>
void bubbleSort( T arr[] , int n){

    int new_n; 
    do{
        new_n = 0;
        for( int i = 1 ; i < n ; i ++ )
            if( arr[i-1] > arr[i] ){
                swap( arr[i-1] , arr[i] );
                new_n = i;
            }
        n = new_n;
    }while(new_n > 0);
}

 

1.5 相关性质

• 时间复杂度: O(n²) 　
• 空间复杂度：O(1)
• 稳定排序　　　　　　
• 原地排序

 

 

2.选择排序（selection sort）

2.1 算法过程：

　　首先在未排序的序列（通常就是整个序列）中找到最小的元素，来放到序列的头部；然后再从剩余的未排序的序列中寻找最小元素，放到有序序列的最尾端。

　　如此重复，直到整个序列都是有序的。

2.2 可视化展示：

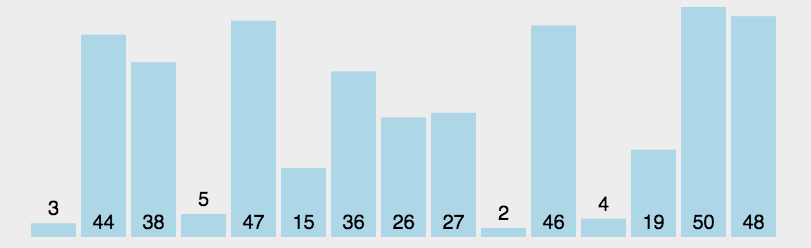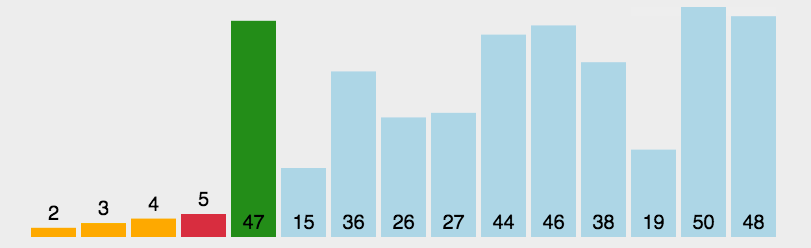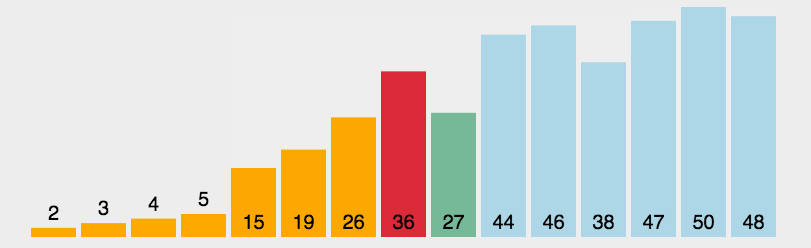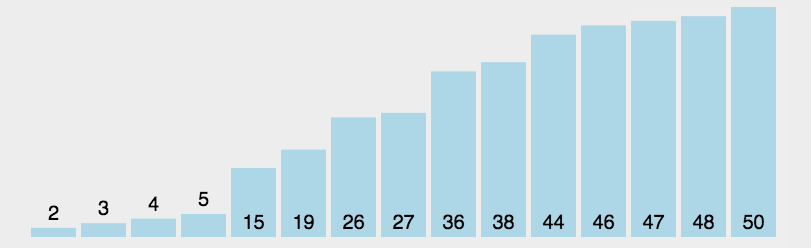
图源：https://juejin.im/post/5b4ef0bbe51d4519575a18d0

2.3 代码实现：　　

 python版本：

def selection_sort(nums):
    length = len(nums)
    if(length==0):
        return nums
    for i in range(length):
        argmin = i
        for j in range(i,length):
            if(nums[j]<nums[argmin]):
                argmin = j
        nums[i],nums[argmin] = nums[argmin],nums[i]
    return nums

 C++版本：

template<typename T>
void selectionSort(T arr[], int n){

    for(int i = 0 ; i < n ; i ++){

        int minIndex = i;
        for( int j = i + 1 ; j < n ; j ++ )
            if( arr[j] < arr[minIndex] )
                minIndex = j;

        swap( arr[i] , arr[minIndex] );
    }
}

 

2.4 相关性质：

• 时间复杂度：O(n²)  （无论什么数据都是，稳）
• 空间复杂度：O(1)
• 稳定性取决于具体实现方法
• 原地排序

 

3.插入排序（insertion sort）

3.1 算法过程：

　　将第一个元素看作是一个有序序列，第二个元素到最后一个元素看作是无序的。对于无序序列的每一个元素，放到有序序列的合适位置，变成新的有序序列，如此反复知道整个序列变成有序序列。（如果遇到相等元素的放在该元素的后面）

        通俗理解：类比拿到扑克牌时，拿到第一张扑克牌时，该扑克牌就是一个有序序列。每次取到一张新的扑克牌将其放在合适的位置，如此往复。

3.2 可视化展示：

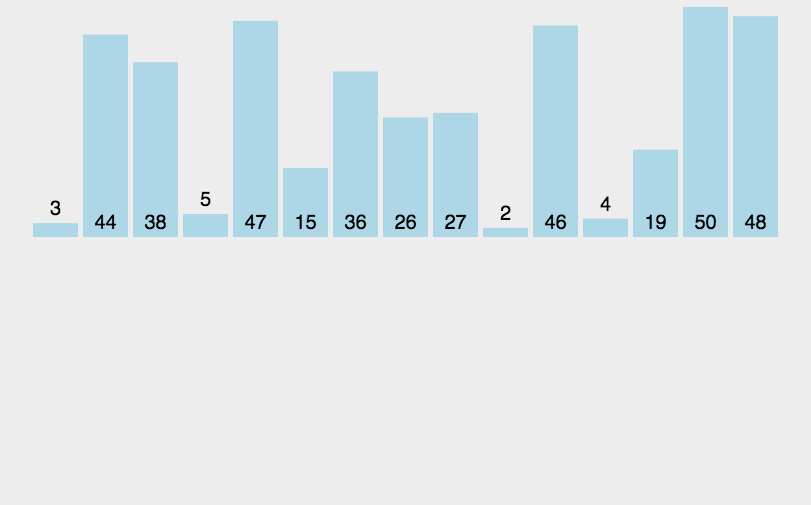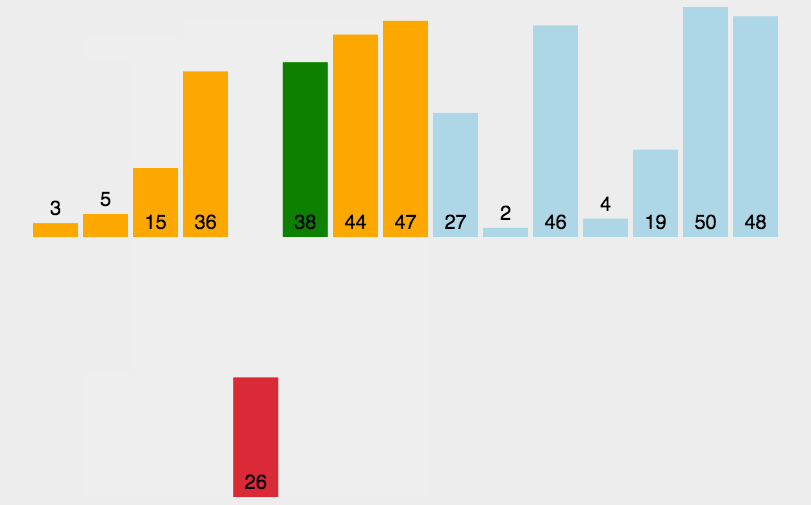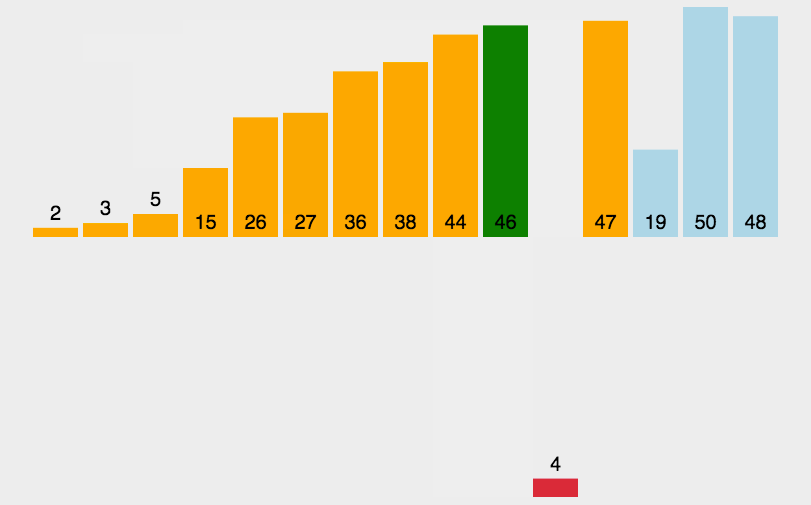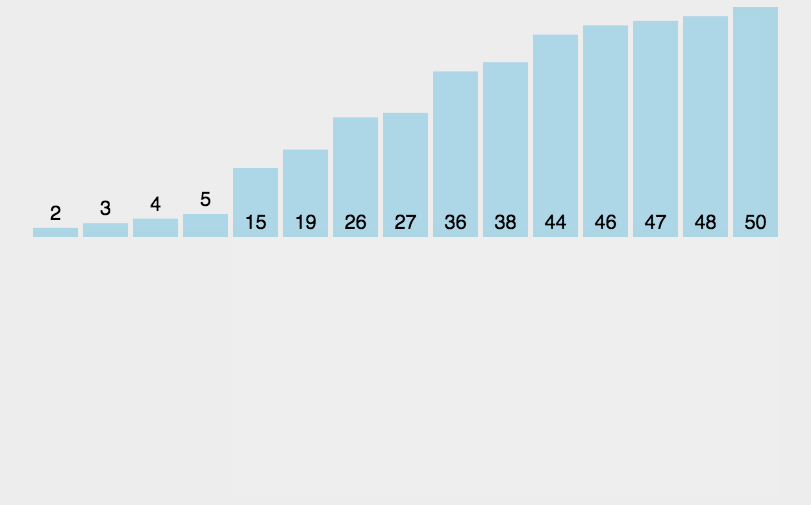
 　　图源：https://juejin.im/post/5b4ef681f265da0f4b7a8d44

 3.3 代码实现：

 python版本：

def insertion_sort(nums):
    length = len(nums)
    if(length==0):
        return nums
    for i in range(length):
        pre = i-1
        cur_num = nums[i]
        while pre>=0 and nums[pre]>cur_num:
            nums[pre+1] = nums[pre]
            pre -= 1
        nums[pre+1] = cur_num  # 选择最后再交换这个元素
    return nums

C++版本：

template<typename T>
void insertionSort(T arr[], int n) {
    
    for (int i = 1; i < n; i++) {
        //寻找元素arr[i]合适的插入位置
        for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {
            swap(arr[j], arr[j - 1]);
        }
    }
}

 

3.4 算法改进：

　　改进：先不进行swap，而是拷贝一份先前进行比较，找到合适的位置后再做赋值操作

       实现（C++）（上面python代码已经实现了）：

template<typename T>
void insertionSortImprove(T arr[], int n) {

    for (int i = 1; i < n; i++) {
        //寻找元素arr[i]合适的插入位置
        T e = arr[i];
        int j;
        for ( j = i; j > 0 && arr[j-1] > e; j--) {
            arr[j] = arr[j - 1];
        }
        arr[j] = e;
    }
}

 

3.5 相关性质：　

• 时间复杂度：O(n²)   最好的情况下是O(n),平均比较和移动次数约为 (n^2)/4

　　（插入排序法的提前退出循环的特性，使得在面对一个有序性强的数组时，性能非常优异）

　　（插入排序法理论上来说可以提前跳出循环，速度应该快于选择排序法，但由于多次交换的赋值操作使得时间变长。这说明算法实际的运行速度还受限于实现方式，例如递归时开辟栈空间的开销，交换操作的开销等等）

• 空间复杂度：O(1)
• 稳定排序
• 原地排序

 

4.插入排序的衍生算法--希尔排序

1959年Shell发明，第一个突破O(n²)的排序算法

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率。但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位，因此如果一次可以移动多位，也就是有一个间隔，就有了希尔排序的思路。

4.1 算法过程

　　基本思想：先将整个待排序的序列分割成为若干子序列分别进行插入排序，等到整个序列中基本有序时，再对整个序列进行插入排序。

　　具体过程：

1. 选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1；

2. 按增量序列个数 k，对序列进行 k 趟排序；

3. 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

        来张图帮助理解：

  

 

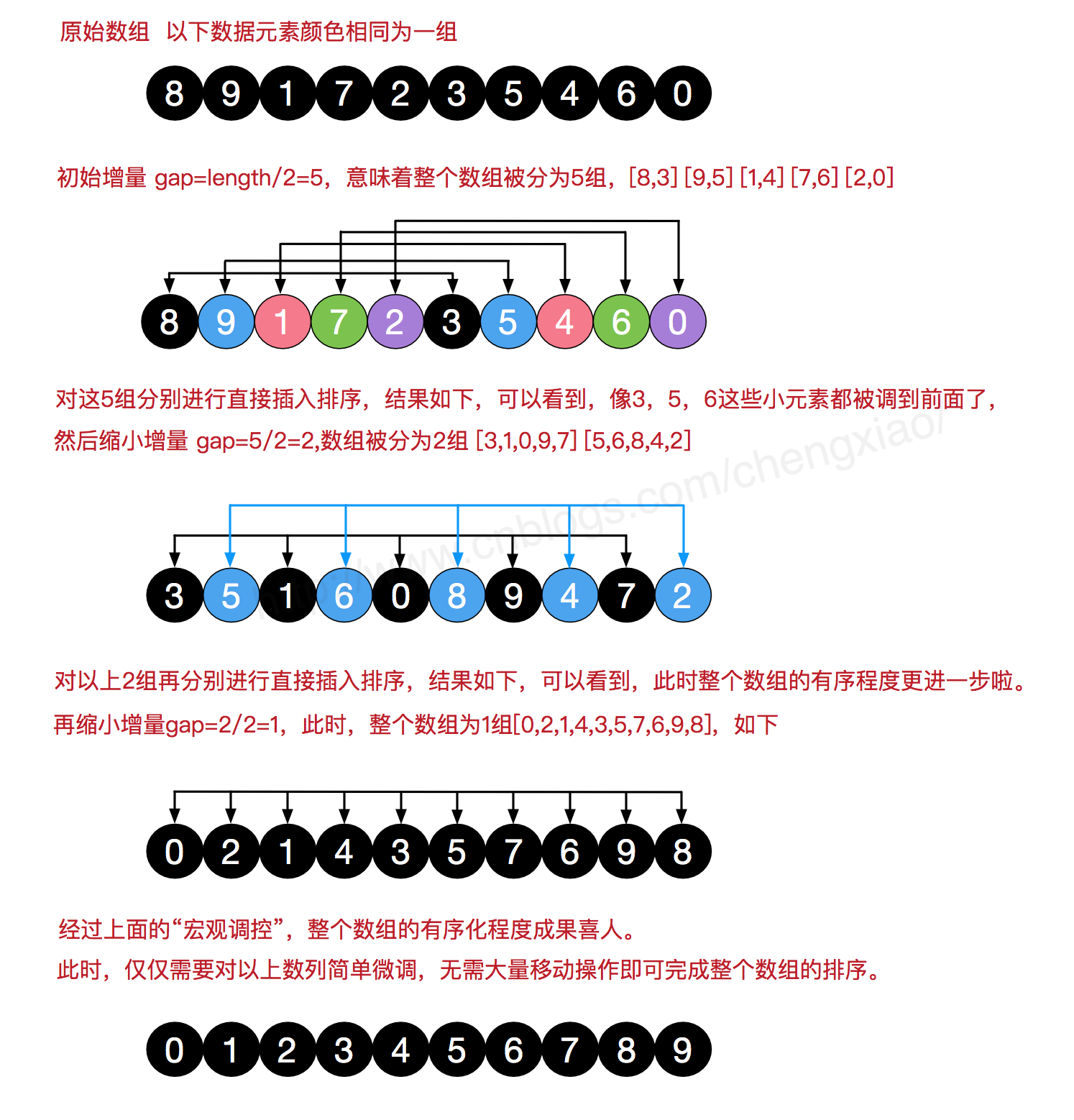
　　图源：https://www.cnblogs.com/chengxiao/p/6104371.html

 

4.2 可视化展示：

 

图源：https://juejin.im/post/5bf9f2285188256b0f5832a0

 

4.3 代码实现：

　　由于原始的希尔增量序列不互质，可能会出现增量序列不起作用的情况，故在此不使用希尔增量序列。

 python版本：

import math #使用math.floor()来对增量进行取整
def shell_sort(nums):
    length = len(nums)
    if(length==0):
        return nums
    offset = 1
    while(offset<length/3):
        offset = offset*3 + 1
    while offset>0:
        for i in range(offset,length):
            tmp = nums[i]
            j = i-offset
            while j>=0 and nums[j] > tmp:
                nums[j+offset] = nums[j]
                j -= offset
            nums[j+offset] = tmp
        offset = math.floor(offset/3)
    return nums

  C++版本：

template<typename T>
void shellSort(T arr[], int n){

    // 计算增量序列: 1, 4, 13, 40, 121, 364, 1093...
    int offset = 1;
    while( offset < n/3 )
        offset = 3 * offset + 1;

    while( offset >= 1 ){

        for( int i = offset ; i < n ; i ++ ){

            // 对 arr[i], arr[i-offset ], arr[i-2*offset ], arr[i-3*offset ]... 使用插入排序
            T e = arr[i];
            int j;
            for( j = i ; j >= offset && e < arr[j-offset ] ; j -= offset )
                arr[j] = arr[j-offset ];
            arr[j] = e;
        }

        offset /= 3;
    }
}

4.4 希尔排序的增量序列：

• shell 增量序列 ： k = k/2
• Hibbard增量序列：Dk = 2^k-1 相邻元素互质
• Sedgewick增量序列：9*4^i - 9*2^i +1 或 4^i - 3*2^i +1
• 更多的增量序列以及代码实现

4.5 相关性质：

• 时间复杂度：希尔排序的复杂度与增量序列的选择有关。具体分析可以参考：

  排序：希尔排序（算法）

• 空间复杂度： O(1) 
• 不稳定排序
• 原地排序

 

END