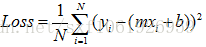广告数据线性回归分析
线性回归
线性回归是最基础的机器学习算法,它是用一条直线去拟合数据,适用于线性数据。
线性回归包括一元线性回归和多元线性回归,一元的是只有一个x和一个y。多元的是指有多个x和一个y。
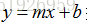
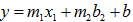 (多元)
(多元)
我们希望这些点尽量离这条直线近一点。即去找每个点和直线的距离 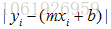
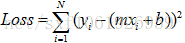
即
下面是利用广告数据进行线性回归模型的应用:
如果市场的运营部门给了你一份数据,数据包含了不同广告渠道的成本及对应的产品销售量。现在的问题是:
- 哪些渠道的广告真正影响了销售量?
- 根据已知的渠道预算,如何实现销售量的预测?
- 模型预测的好坏,该如何评估?
利用Python建模
哪些渠道的广告真正影响了销售量?对于这个问题的回答,其实就是在构建多元线性回归模型后,需要对偏回归系数进行显著性检验,把那些显著的变量保留下来,即可以认为这些变量对销售量是存在影响的。关于线性回归模型的落地,我们这里推荐使用statsmodels模块,因为该模块相比于sklearn,可以得到更多关于模型的详细信息
广告数据下载地址:https://pan.baidu.com/s/1qYNsP0w 密码: 2g3f
数据导入和描述统计:
import os import codecs import numpy as np import pandas as pd import matplotlib.pyplot as plt import statsmodels.formula.api as smf from sklearn.cross_validation import train_test_split from sklearn.metrics import mean_squared_error os.getcwd() os.chdir("C:/Users/admin/Desktop/ml-100k") f=codecs.open('Advertising.csv', 'r') #print (f.read()) #header = ['tv', 'radio', 'newspaper','sales'] sales=pd.read_csv('Advertising.csv',sep=',') print(sales) sales.describe()
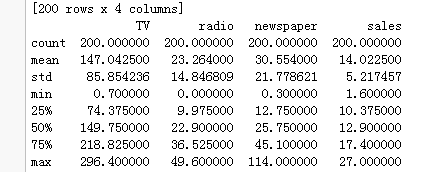
通过数据的描述性统计分析,我们可以得到这些数值变量的基本统计值,如均值、最小值、最大值、下四分位、上四分位、标准差,而这些统计值有助于你对数据的理解和分布的解读。接下来需要根据读取进来的数据构造回归模型,但建模之前,我们一般需要将数据集拆分成训练集(用于建模)和测试集(用于模型的评估)两个部分。
Train,Test = train_test_split(sales, train_size = 0.8, random_state= 1234)
# 建模
fit = smf.ols( ‘sales~TV+radio+newspaper’, data = Train).fit()
#模型信息反馈
fit2.summary()
# 第一个模型的预测结果
pred = fit.predict(exog = Test)
通过模型反馈的结果我们可知,模型是通过显著性检验的,即F统计量所对应的P值是远远小于0.05这个阈值的,说明需要拒绝原假设(即认为模型的所有回归系数都不全为0)。
去掉newspaper,重新建模
fit2 = smf.ols( ‘sales~TV+radio’, data = Train.drop( ‘newspaper’, axis = 1)).fit()
# 模型信息反馈
fit2.summary()
附代码
#构造训练集和测试集 Train,Test = train_test_split(sales, train_size = 0.8, random_state= 1234) #建模 fit = smf.ols('sales~TV+radio+newspaper', data = Train).fit() #重新建模 fit2=smf.ols('sales~TV+radio',data=Train.drop(columns='newspaper',axis=1)).fit() #模型信息反馈 fit2.summary()
通过第二次建模(模型中剔除了newspaper这个变量),结果非常明朗,一方面模型通过了显著性检验,另一方面,所有的变量也通过了显著性检验。那问题来了,难道你剔除了newspaper这个变量后,模型效果确实变好了吗?验证一个模型好不好,只需要将预测值和真实值做一个对比即可,如果模型越优秀,那预测出来的结果应该会更接近与现实数据。接下来,我们就基于fit和fit2这两个模型,分别在Test数据集上做预测:
# 第一个模型的预测结果 pred = fit.predict(exog = Test) # 第二个模型的预测结果 pred2 = fit2.predict(exog = Test.drop(columns='newspaper', axis = 1)) #模型效果对比 RMSE = np.sqrt(mean_squared_error(Test.sales, pred)) RMSE2 = np.sqrt(mean_squared_error(Test.sales, pred2)) print( '第一个模型的预测效果:RMES=%.4f\n'%RMSE) print( '第二个模型的预测效果:RMES=%.4f\n'%RMSE2)

对于连续变量预测效果的好坏,我们可以借助于RMSE(均方根误差,即真实值与预测值的均方根)来衡量,如果这个值越小,就说明模型越优秀,即预测出来的值会越接近于真实值。很明显,模型2的RMSE相比于模型1会小一些,模型会更符合实际。最后,我们再利用可视化的方法来刻画真实的观测点与拟合线之间的关系:
# 真实值与预测值的关系# 设置绘图风格 plt.style.use( 'ggplot') # 设置中文编码和负号的正常显示 plt.rcParams['font.sans-serif'] = 'Microsoft YaHei' # 散点图 plt.scatter(Test.sales, pred, label = '观测点') # 回归线 plt.plot([Test.sales.min(),Test.sales.max()],[pred.min(),pred.max()],'r-',lw= 2,label = '拟合线') # 添加轴标签和标题 plt.title('真实值VS.预测值') plt.xlabel('真实值') plt.ylabel('预测值') #去除图边框的顶部刻度和右边刻度 plt.tick_params(top = 'off', right = 'off') # 添加图例 plt.legend(loc = 'upper left') # 图形展现 plt.show()
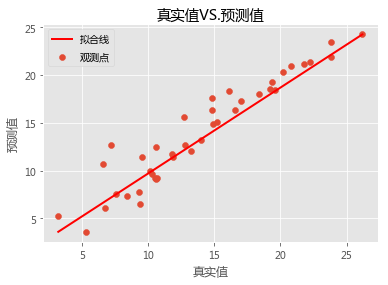
从上面的关系图来看,模型确实拟合的还是蛮不错的,这些真实点基本上都在拟合线附近,并没有产生太大的差异。
原文地址:http://www.ppvke.com/Blog/archives/53081