多项式乘法
给定两个多项式
求
前置知识
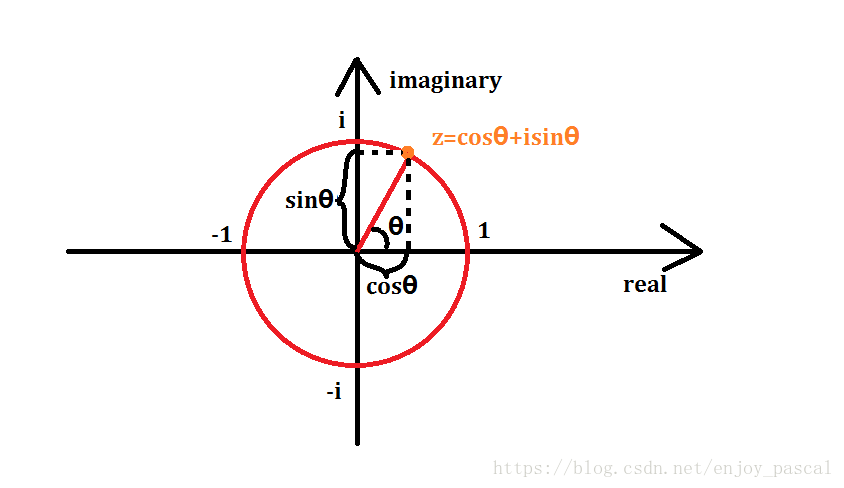
单位根
次单位根即为满足 的 x。
由代数基本定理可得 次单位根应该有 个。
第 个记为 。
单位根的一些性质
原根的性质( 为质数)
多项式的点表示法
众所周知,一个 次多项式可以用 个互异的点表示出来。
这就叫做多项式的点表示法。
DFT
上面的点表示法启示我们了一种求多项式乘法的方法。
一个 次的多项式 ,对于取值 ,可以求出。
同理一个 次的多项式 ,也可以求出相对应的 。
然后我们对于每一个 可以求出一个对应的 。
得到了 ,我们就可以用拉格朗日插值法求出多项式 了。
当我们将取值 取为 时我们就可以少算很多的次幂。
利用上述方法求多项式乘法的方法就叫做 DFT。
FFT
上面的 DFT 虽然看起来很妙,但仍然是 的,其主要复杂度为求出对应的 和 。
我们考虑优化这个过程。
接下来的过程中我们假设 为 的整数次幂。
按照 次数的奇偶分类。
记
则 。
显然 和 都为 次多项式。
接下来就是 FFT 的核心。
对于所有 ,有
然后我们就发现了一个很神奇的东西,如果我们知道了 和 我们就可以同时求出 和 。
并且由于 和 都为 次多项式,我们可以用相同的办法求出他们,并且每次将次数缩小到 。
当递归到 次时直接带入求值即可。
这就是一个类似于分治的复杂度了,不难证明这个过程是 的。
不过我们仍然还有问题需要解决,上面我们只优化了求出对应的点坐标的复杂度,并没有优化求出系数的复杂度,如果我们用拉格朗日插值来求出系数这个算法的复杂度还是 的。
但这就是 DFT 的优越之处,它的特殊取值使得它可以同样在 的复杂度内求出对应的系数。
IFFT
IFFT 即将点值变为系数的过程。
有个比较神奇的结论,记我们通过 FFT 算出来的结果的乘积为 。
记多项式 在 处的取值为 。
有 。
即 。
IFFT 证明
记 。
根据等比数列求和公式,首项为 ,公比为 ,当公比不为 ,即 时,有:
当 时,有:
所以不难得出
FFT 未优化代码
#include <bits/stdc++.h> using namespace std; namespace Math { #define PI 3.14159265358979323846 struct Complex { double r, i; Complex(double r = 0, double i = 0): r(r), i(i) { } }; Complex operator + (const Complex &a, const Complex &b) { return { a.r + b.r, a.i + b.i }; } Complex operator - (const Complex &a, const Complex &b) { return { a.r - b.r, a.i - b.i }; } Complex operator * (const Complex &a, const Complex &b) { return { a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r }; } void FFT(int len, vector<Complex> &a, int op) { if (len == 1) return; vector<Complex> a1(len / 2), a2(len / 2); for (int i = 0; i < a.size(); i += 2) a1[i / 2] = a[i], a2[i / 2] = a[i + 1]; FFT(len / 2, a1, op), FFT(len / 2, a2, op); Complex step = { cos(PI * 2 / len), op * sin(PI * 2 / len) }, omega = { 1, 0 }; for (int i = 0; i < len / 2; i ++, omega = omega * step) a[i] = a1[i] + omega * a2[i], a[i + len / 2] = a1[i] - omega * a2[i]; } vector<int> polyMul(vector<int> a, vector<int> b) { int n = a.size(), m = b.size(); int len = 1; while (len < n + m - 1) len *= 2; vector<Complex> ac(len), bc(len); Complex init = { 0, 0 }; for (int i = 0; i < len; i ++) ac[i] = (i < n ? a[i] : init); for (int i = 0; i < len; i ++) bc[i] = (i < m ? b[i] : init); FFT(len, ac, 1), FFT(len, bc, 1); // FFT vector<Complex> cc(len); for (int i = 0; i < len; i ++) cc[i] = ac[i] * bc[i]; FFT(len, cc, -1); // IFFT vector<int> c(n + m - 1); for (int i = 0; i < n + m - 1; i ++) c[i] = cc[i].r / len + 0.5; return c; } #undef PI } int main() { int n, m; scanf("%d%d", &n, &m); vector<int> a(n + 1), b(m + 1); for (int i = 0; i <= n; i ++) scanf("%d", &a[i]); for (int i = 0; i <= m; i ++) scanf("%d", &b[i]); vector<int> c = Math::polyMul(a, b); for (int i = 0; i < c.size(); i ++) printf("%d ", c[i]); return 0; }
虽然看网上博客说分治版本的 FFT 没法通过洛谷的模板题,但我莫名其妙过了……
但是常数确实是比较大的。
FFT 优化
主要是可以优化掉递归的常数。
不难发现可以直接通过下表二进制反转后分组来规避掉递归的常数。(为什么?因为奇偶分组是用最低位来决定的,所以考虑这个序列最终的顺序就应该倒过来)
代码:
#include <bits/stdc++.h> using namespace std; namespace Math { #define PI 3.14159265358979323846 struct Complex { double r, i; Complex(double r = 0, double i = 0): r(r), i(i) { } }; Complex operator + (const Complex &a, const Complex &b) { return { a.r + b.r, a.i + b.i }; } Complex operator - (const Complex &a, const Complex &b) { return { a.r - b.r, a.i - b.i }; } Complex operator * (const Complex &a, const Complex &b) { return { a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r }; } vector<int> rev; void init_FFT(int len, int cnt) { rev.resize(len); for (int i = 0; i < len; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (cnt - 1)); } // fast implement void FFT(int len, vector<Complex> &a, int op) { for (int i = 0; i < len; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]); for (int t = 1; t < len; t <<= 1) { Complex step = { cos(PI / t), op * sin(PI / t) }; for (int i = 0; i < len; i += 2 * t) { Complex omega = { 1, 0 }; for (int j = i; j < i + t; j ++, omega = omega * step) { Complex x = a[j], y = omega * a[j + t]; a[j] = x + y, a[j + t] = x - y; } } } } vector<int> polyMul(vector<int> a, vector<int> b) { int n = a.size(), m = b.size(); int len = 1, cnt = 0; while (len < n + m - 1) len *= 2, ++ cnt; init_FFT(len, cnt); vector<Complex> ac(len), bc(len); Complex init = { 0, 0 }; for (int i = 0; i < len; i ++) ac[i] = (i < n ? a[i] : init); for (int i = 0; i < len; i ++) bc[i] = (i < m ? b[i] : init); FFT(len, ac, 1), FFT(len, bc, 1); // FFT vector<Complex> cc(len); for (int i = 0; i < len; i ++) cc[i] = ac[i] * bc[i]; FFT(len, cc, -1); // IFFT vector<int> c(n + m - 1); for (int i = 0; i < n + m - 1; i ++) c[i] = cc[i].r / len + 0.5; return c; } #undef PI } int main() { int n, m; scanf("%d%d", &n, &m); vector<int> a(n + 1), b(m + 1); for (int i = 0; i <= n; i ++) scanf("%d", &a[i]); for (int i = 0; i <= m; i ++) scanf("%d", &b[i]); vector<int> c = Math::polyMul(a, b); for (int i = 0; i < c.size(); i ++) printf("%d ", c[i]); return 0; }
优化掉了一秒,可喜可贺。
NTT
FFT 中由于要使用单位根,精度是一个很大的问题,所以就有了 NTT。
在下文中, 为 的整数次幂, 为质数且 , 为 的一个原根。
我们设 。
那么 就有一些和单位根一样优秀的性质。
可以发现在 FFT 中使用到的单位根的性质原根全部满足。
所以我们就可以使用原根来代替单位根了。
质数我们一般选择 因为 有因子 。
原根我们一般使用 ,好记。
NTT 代码
#include <bits/stdc++.h> using namespace std; namespace Math { typedef long long ll; const ll MOD = 998244353; const ll G = 3; const ll GINV = 332748118; vector<int> rev; void init_NTT(int len, int cnt) { rev.resize(len); for (int i = 0; i < len; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (cnt - 1)); } ll qpow(ll a, ll b) { ll ret = 1; for (; b; b >>= 1) { if (b & 1) ret = ret * a % MOD; a = a * a % MOD; } return ret; } void NTT(int len, vector<int> &a, int op) { for (int i = 0; i < len; i ++) if (i < rev[i]) swap(a[i], a[rev[i]]); for (int t = 1; t < len; t <<= 1) { ll h = qpow(op ? G : GINV, (MOD - 1) / (t * 2)); for (int i = 0; i < len; i += 2 * t) { ll w = 1; for (int j = i; j < i + t; j ++, w = w * h % MOD) { ll x = a[j], y = w * a[j + t] % MOD; a[j] = (x + y) % MOD, a[j + t] = (x - y + MOD) % MOD; } } } } vector<int> polyMul(vector<int> a, vector<int> b) { int n = a.size(), m = b.size(); int len = 1, cnt = 0; while (len < n + m - 1) len *= 2, ++ cnt; init_NTT(len, cnt); a.resize(len), b.resize(len); NTT(len, a, 1), NTT(len, b, 1); vector<int> c(len); for (int i = 0; i < len; i ++) c[i] = 1ll * a[i] * b[i] % MOD; NTT(len, c, 0); ll inv = qpow(len, MOD - 2); c.resize(n + m - 1); for (int i = 0; i < n + m - 1; i ++) c[i] = inv * c[i] % MOD; return c; } } int main() { int n, m; scanf("%d%d", &n, &m); vector<int> a(n + 1), b(m + 1); for (int i = 0; i <= n; i ++) scanf("%d", &a[i]); for (int i = 0; i <= m; i ++) scanf("%d", &b[i]); vector<int> c = Math::polyMul(a, b); for (int i = 0; i < c.size(); i ++) printf("%d ", c[i]); return 0; }
确实快了不止一点。
完结撒花!




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】