哈夫曼树以及哈夫曼编码的问题
今天看到一个哈夫曼编码的题目,给定一个字符串abcdabaa,问哈夫曼编码后的二进制串的总长度是多少,答案是14
对于哈夫曼树我是一点都不了解啊,所以一顿查找,总结出以下知识点,与大家分享:当然部分内容参考了下百度
哈夫曼树又称为最优二叉树,是一种带权路径最短的二叉树。哈夫曼树是二叉树的一种应用,在信息检索中很常用。
一些相关的概念:
1、节点之间的路径长度:从一个节点到另一个节点之间的分支数量称为两个节点之间的路径长度。
2、树的路径长度:从根节点到树中每一个节点的路径长度之和。
3、节点的带权路径长度:从该节点到根节点之间的路径长度与节点的权的乘积。
4、树的带权路径长度:树中所有叶子节点的带权路径长度之和。
带权路径最小的二叉树被称为哈夫曼树或最优二叉树。
对于哈夫曼树,有一个很重要的定理:对于具有n个叶子节点的哈夫曼树,一共需要2*n-1个节点。
这个定理的解释如下:对于二叉树来说,有三种类型节点,即度数(只算出度)为2的节点,度数为1的节点和度数为0的叶节点。而哈夫曼树的非叶子节点是由两个节点生成的,因此不能出现度数为1的节点,而生成的非叶子节点的个数为叶子节点个数减一,于此定理就得证了。
构造哈夫曼树的算法如下:
1)对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F={T1,T2,T3,...,Ti,..., Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。
2)在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
3)从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
4)重复2)和3),直到集合F中只有一棵二叉树为止。
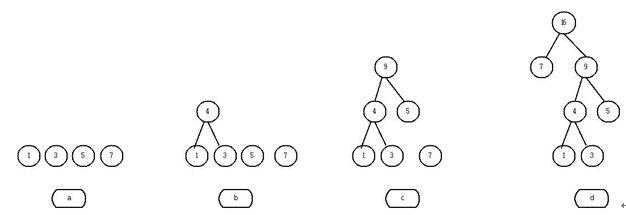
可以计算得到该哈夫曼树的路径长度WPL=(1+3)*3+2*5+1*7=26。
哈夫曼编码:
根据哈夫曼树可以解决报文编码问题。假设需要一个字符串“abcdabcaba”进行编码,将它转换为唯一的二进制码,但要求转换出来的二进制编码的长度最小。
假设每个字符在字符串中出现频率为W,其编码长度为L,编码字符n个,则编码后二进制码的总长度为W1L1+W2L2+…+WnLn,这恰好是哈夫曼树的处理原则。因此可以采用哈夫曼树的构造原理进行二进制编码,从而使得电文长度最短。
对于“abcdabcaba”,共有a、b、c、d4个字符,出现次数分别为4、3、2、1,相当于它们的权值,将a、b、c、d以出现次数为权值构造哈夫曼树,得到下左图的结果。
从哈夫曼树根节点开始,对左子树分配代码“0”,对右子树分配“1”,一直到达叶子节点。然后,将从树根沿着每条路径到达叶子节点的代码排列起来,便得到每个叶子节点的哈夫曼编码,如下右图。

从图中可以看出,a、b、c、d对应的编码分别为0、10、110、111,然后将字符串“abcdabcaba”转换为对应的二进制码就是0101101110101100100,长度仅为19。这也就是最短二进制编码,也称为哈夫曼编码。
根据上面介绍的规律不难发现:哈夫曼编码有一个规律:假设有N个叶子节点需要编码,最终得到的哈夫曼树一定有N层,哈夫曼编码得到的二进制码的最大长度为N-1。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 【自荐】一款简洁、开源的在线白板工具 Drawnix