[7.5~7.12 做题记录]
[7.5~7.12 做题记录]
环形DP
环路运输
环形DP，考虑把圆形公路从 \(N，1\) 处断开并复制，搞成 \(1 \sim 2\times n\) 的直线公路，对于原位置 \(i\)，现在有两个位置 \(i,n+i\)，而 \([i-\frac{n}{2},i]\) 和 \([n+i-\frac{n}{2},n+i]\) 可以确保所有点对都被计算且对于 \(j \in [i-\frac{n}{2},i],i\in [1,2\times n]\)，\(dis_{i,j}\) 等于 \(i-j\) 或是 \(n+i-j\)，这样就不必分讨了。
接下来，考虑 \(i,j\) 间代价为 \(A_i+A_j+i-j\)，其中 \(A_i+i\) 不变，使 \(A_j-j\) 最大即可。那么使用单调队列优化，每次清除下标不合法的解，队头统计答案，再加入当前 \(A_i-i\)，并维持单调性。
CODE
for(int i=1;i<=n;i++) a[i]=a[n+i]=read;
int n2=n<<1;
head=tail=1;q[tail]=0;
for(int i=1;i<=n2;i++){
while(head<=tail && q[head]<i-n/2) head++;
ans=max(ans,a[i]+a[q[head]]+i-q[head]);
while(a[i]-i>=a[q[tail]]-q[tail] && head<=tail) tail--;
q[++tail]=i;
}
write(ans);
高斯消元
高斯回带消元
具体讲解请上luogu，这里简单概括。
处理成上三角矩阵，然后回带即可。但是要处理究竟是无解还是无数解，需要定义 \(r\) 为主元个数，即最后系数不为 \(0\) 的。最后对于剩下的自由元进行判定，如果常数项不为 \(0\)，必然无解，否则无数解，注意无解优先级要大于无数解。
代码见注释，不对，注释见代码……
回带消元
#define eqs 1e-12
int gauss(){
int r=1;
for(int i=1;i<=n;i++){
int k=r;
for(int j=r+1;j<=n;j++)
if(fabs(a[k][i])<fabs(a[j][i])) k=j;
if(r!=k) swap(a[r],a[k]);
//在这一列找系数尽可能大的来算主元，据说可以更精确，同时如果 k=0 说明该元为自由元
double div=a[r][i];
if(fabs(div)<eqs) continue;//如果是自由元，直接不理，后期它一定会被换到下面
for(int j=i;j<=n+1;j++) a[r][j]/=div;
for(int j=r+1;j<=n;j++){
div=a[j][i];
for(int k=i;k<=n+1;k++)
a[j][k]-=a[r][k]*div;
}
//等式性质、加减消元
++r;
}
for(int i=r;i<=n;i++){
if(fabs(a[i][n+1])>eqs) return -1;//判无解
}
if(r<=n) return 0;//判无数解
ans[n]=a[n][n+1];//回带
for(int i=n-1;i>=1;--i){
ans[i]=a[i][n+1];
for(int j=i+1;j<=n;j++){
ans[i]-=a[i][j]*ans[j];
}
}
return 1;
}
高斯约旦消元
基本思路与回带一样，但是最后不用回带，直接处理成一条对角线既是答案，那么就在消元时消整列即可。
约旦消元
#define eqs 1e-12
int gauss(){
int r=1;
for(int i=1;i<=n;i++){
int k=r;
for(int j=r+1;j<=n;j++)
if(fabs(a[k][i])<fabs(a[j][i])) k=j;
if(k!=r) swap(a[k],a[r]);
if(fabs(a[r][i])<eqs) continue;
double div=a[r][i];
for(int j=i;j<=n+1;j++) a[r][j]/=div;
for(int j=1;j<=n;j++){//整列消
if(j==r) continue;
div=a[j][i];
for(int k=i;k<=n+1;k++){
a[j][k]-=a[r][k]*div;
}
}
r++;
}
for(int i=r;i<=n;i++)
if(fabs(a[i][n+1])>eqs)return -1;
if(r<=n) return 0;
for(int i=1;i<=n;i++) ans[i]=a[i][n+1]/a[i][i];
return 1;
}
[例题]Broken robot
这是一道后效性DP，需要高斯消元处理。
因为机器人可以左右走，所以第 \(i\) 行的状态会互相影响，不能递推求解，因此考虑高斯消元。
首先当然还是 DP，期望 DP，方便起见还是倒推，设 \(dp_{i,j}\) 为从 \((i,j)\) 走到最后一行的期望步数，初始 \(dp_{n,j}=0\)，接下来考虑 DP 转移：
\[dp_{i,j}=\begin{cases} 1+\frac{1}{3}dp_{i,1}+\frac{1}{3}dp_{i,2}+\frac{1}{3}dp_{i+1,1},j=1 \\ 1+\frac{1}{4}dp_{i,j}+\frac{1}{4}dp_{i,j+1}+\frac{1}{4}dp_{i,j-1}+\frac{1}{4}dp_{i+1,j},1<j<m \\ 1+\frac{1}{3}dp_{i,m}+\frac{1}{3}dp_{i,m-1}+\frac{1}{3}dp_{i+1,m},j=m \end{cases}
\]
这显然不能递推转移，因此我们考虑高斯消元：
- 我们发现，原式移项化简后，由于第 \(i+1\) 行已经算完，可以当做已知量，所以：
\[\begin{cases} \frac{2}{3}dp_{i,1}-\frac{1}{3}dp_{i,2} &=1+\frac{1}{3}dp_{i+1,1} \\ -\frac{1}{4}dp_{i,j-1}+ \frac{3}{4}dp_{i,j}-\frac{1}{4}dp_{i,j+1} &=1+\frac{1}{4}dp_{i+1,j},1<j<m \\ -\frac{1}{3}dp_{i,m-1}+\frac{2}{3}dp_{i,m} &=1+\frac{1}{3}dp_{i+1,m} \end{cases}
\]
这就成了一个 \(m\) 元一次方程组，直接高斯消元。
\[ \begin{vmatrix} +\frac{2}{3} & -\frac{1}{3} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & | & 1+\frac{1}{3}dp_{i+1,1} \\
-\frac{1}{4} & +\frac{3}{4} & -\frac{1}{4} & 0 & 0 & 0 & 0 & 0 & 0 & | & 1+\frac{1}{3}dp_{i+1,2} \\
0 & -\frac{1}{4} & +\frac{3}{4} & -\frac{1}{4} & 0 & 0 & 0 & 0 & 0 & | & 1+\frac{1}{3}dp_{i+1,3} \\
0 & 0 & -\frac{1}{4} & +\frac{3}{4} & -\frac{1}{4} & 0 & 0 & 0 & 0 & | & 1+\frac{1}{3}dp_{i+1,4} \\
0 & 0 & 0 & -\frac{1}{4} & +\frac{3}{4} & -\frac{1}{4} & 0 & 0 & 0 & | & 1+\frac{1}{3}dp_{i+1,5} \\
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & | & \vdots \\
0 & 0 & 0 & 0 & 0 & 0 & -\frac{1}{4} & +\frac{3}{4} & -\frac{1}{4} & | & 1+\frac{1}{3}dp_{i+1,6} \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & -\frac{1}{3} & +\frac{2}{3} & | & 1+dp_{i+1,m}\end{vmatrix} \]
这是一个 带状矩阵 (Hangry_Sol 瑞平，像个棺材)，我们知道普通的 \(n^3\) 高斯消元在 \(n\leq 10^3\) 的数据范围直接会祭，而带状矩阵其实有很多 \(0\) 不用消，每行只需要消 \(d\) 的范围，最后就成了优秀的 \(O(m\times d^2)\) 做法，\(d^2\) 直接当常数，总复杂度 \(O(m\times n)\) 肆意过。
随后 \(dp_{x,y}\) 即为所求。
CODE
#include<bits/stdc++.h>
using namespace std;
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
#define N 1010
#define eqs 1e-7
const int d = 2;
int n,m;
int x,y;
double dp[N][N];
double a[N][N];
void gauss(int s){
for(int i=1;i<=m;i++){
if(fabs(a[i][i])<eqs){
for(int j=i+1;j<=min(m,i+d);j++)
if(fabs(a[j][i]) > fabs(a[i][i])){
swap(a[j],a[i]);
break;
}
}
if(fabs(a[i][i])<eqs) continue;
double div=a[i][i];
for(int j=i;j<=min(i+2*d,m);j++) a[i][j]/=div;
a[i][m+1]/=div;
for(int j=i+1;j<=min(i+d,m);j++){
div=a[j][i];
for(int k=i;k<=min(i+2*d,m);k++)
a[j][k]-=a[i][k]*div;
a[j][m+1]-=a[i][m+1]*div;
}
}
dp[s][m]=a[m][m+1];
for(int i=m-1;i>=1;--i){
dp[s][i]=a[i][m+1];
for(int j=i+1;j<=(i+2*d,m);j++)
dp[s][i]-=dp[s][j]*a[i][j],a[i][j]=0;
}
}
signed main(){
n=read,m=read,x=read,y=read;
if(m==1){
printf("%.2lf",(n-x)*2.0);return 0;
}
for(int i=n-1;i>=1;i--){
a[1][1]=a[m][m]=2.0/3;
a[1][2]=a[m][m-1]=-1.0/3;
a[1][m+1]=1+dp[i+1][1]/3;
a[m][m+1]=1+dp[i+1][m]/3;
for(int j=2;j<=m-1;j++){
a[j][j-1]=a[j][j+1]=-1.0/4;
a[j][j]=3.0/4;
a[j][m+1]=1+dp[i+1][j]/4;
}
gauss(i);
}
printf("%.10lf",dp[x][y]);
return 0;
}
单调队列优化 DP
主要通过对决策变量上下界的单调队列处理，使复杂度大大降低。
[SCOI2010]股票交易
设 \(dp_{i,j}\) 为到第 \(i\) 天手中持 \(j\) 张股票的最大收益。对于第 \(i\) 天，有：
- 第 \(i\) 天在原先无股票前提下购买，即初始值 \(dp_{i,j}=-p.in_a\times j\)
- 第 \(i\) 天不买不卖，\(dp_{i,j}=\max(dp_{i,j},dp_{i-1,j})\)
- 第 \(i\) 天在原有基础上买入，要满足 \(i>w\)。设 \(k\) 为第 \(i-w-1\) 天持有的股票，则 \(dp_{i,j}=\max(dp_{i,j},dp_{i-w-1,k}-(j-k)\times p.in_i)\)，同时要满足 \(k<j\) 且 \(j-k \leq s.in_i\)，即 \(j-s.in_i\leq k<j\)，确定上下界直接跑单调队列即可。
- 第 \(i\) 天在原有基础上卖出，与买入同理，但是要注意 \(j\) 应倒序枚举。
CODE
#include<bits/stdc++.h>
using namespace std;
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
const int N = 2010;
int n;
int p_in[N],p_out[N],s_in[N],s_out[N];
int sumin[N];
int Maxp,w;
int dp[N][N];
int q[N<<1],head,tail;
#define ans1(k) dp[i-w-1][k]+k*p_in[i]
#define ans2(k) dp[i-w-1][k]+k*p_out[i]
int ans=-1e9;
signed main(){
n=read,Maxp=read,w=read;
for(int i=1;i<=n;i++)
p_in[i]=read,p_out[i]=read,s_in[i]=read,s_out[i]=read,sumin[i]=sumin[i-1]+s_in[i];
memset(dp,128,sizeof(dp));
for(int i=1;i<=n;i++)
for(int j=0;j<=s_in[i];j++)
dp[i][j]=-p_in[i]*j;
for(int i=1;i<=n;i++){
for(int j=0;j<=Maxp;j++)
dp[i][j]=max(dp[i][j],dp[i-1][j]);
if(i<w+1) continue;
head=1,tail=0;
for(int j=0;j<=Maxp;j++){
while(head<=tail && q[head]<j-s_in[i]) head++;
if(head<=tail) dp[i][j]=max(dp[i][j],ans1(q[head])-j*p_in[i]);
while(head<=tail && ans1(j)>=ans1(q[tail])) tail--;
q[++tail]=j;
}
head=1,tail=0;
for(int j=Maxp;j>=0;j--){
while(head<=tail && q[head]>j+s_out[i]) head++;
if(head<=tail) dp[i][j]=max(dp[i][j],ans2(q[head])-j*p_out[i]);
while(head<=tail && ans2(j)>=ans2(q[tail])) tail--;
q[++tail]=j;
}
}
for(int j=0;j<=Maxp;j++) ans=max(ans,dp[n][j]);
write(ans);
return 0;
}
[USACO10NOV] Buying Feed G
终于又有自己独立推出来的优化DP了
单调队列优化多重背包，考虑设 \(dp_{i,j}\) 为到第 \(i\) 个店，车上有 \(j\) 吨饲料的最小花费。
- 若在 \(i\) 店不买，则有 \(dp_{i,j}=dp_{i-1,j}+(x_i-x_{i-1})\times j^2\)
- 若在 \(i\) 店买，设在 \(i-1\) 店有 \(k\) 吨饲料，则有 \(dp_{i,j}=\min(dp_{i-1,k}+(x_i-x_{i-1})\times k^2+(j-k)\times c_i)\)，同时要满足 \(k<j\) 且 \(j-k\leq s_i\) (\(s_i\) 为库存)，则有 \(j-s_i\leq k<j\)，直接单调队列。
CODE
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
#define N 510
int m,home,n;
struct Tang{int x,s,c;}t[N];
int dp[N][10010];
int q[N<<1],head,tail;
#define ans(k) dp[i-1][k]+(x(i)-x(i-1))*k*k-k*c(i)
signed main(){
m=read,home=read,n=read;
for(int i=1;i<=n;i++) t[i]={read,read,read};
sort(t+1,t+n+1,[](Tang a,Tang b){return a.x<b.x;});
#define x(i) t[i].x
#define c(i) t[i].c
#define s(i) t[i].s
memset(dp,0x3f,sizeof(dp));
for(int j=0;j<=s(1);j++)
dp[1][j]=c(1)*j;
for(int i=2;i<=n;i++){
dp[i][0]=0;
head=1,tail=0;
q[++tail]=0;
for(int j=1;j<=m;j++){
dp[i][j]=min(dp[i][j],dp[i-1][j]+(x(i)-x(i-1))*j*j);
while(head<=tail && q[head]<j-s(i)) head++;
if(head<=tail) dp[i][j]=min(dp[i][j],ans(q[head])+j*c(i));
while(head<=tail && ans(q[tail])>=ans(j)) tail--;
q[++tail]=j;
}
}
write(dp[n][m]+(home-x(n))*m*m);
return 0;
}
[NOI2005]瑰丽华尔兹
有意思的题。首先考虑 \(O(N\times M \times T)\) 做法，考虑每个时间有使用与不使用魔法两种取 \(\max\)，对于 \(4\) 种方向分讨求解。\(T\) 可以滚动节省空间，但是时间一定祭。
考虑 \(O(N\times M\times K)\) 做法，在某个时间段里，所有时间使用的魔法可以等价成整段时间使用的魔法。那么设 \(dp_{i,j,t}\) 为当前在第 \(t\) 段时间段 结尾，钢琴从 \((x,y)\) 滑到 \((i,j)\) 的最远滑行距离，分讨即可。
-
以上滑为例，即 \(d_t=1\)，有 \(dp_{i,j,t}=\max(dp_{i,j,t-1},dp_{k,i,t-1}+k-j)\)，其中 \((k,j)\) 为 \(t-1\) 时的坐标，那么显然有 \(k>i\) 且 \(k-i\leq s_i\)，上下界，直接单调队列。
-
其他同理，注意枚举顺序即可。
好像把单调队列封装成函数可以只写一个，但是我cai，写了4个单调队列，还因为打错一个数组名调了半小时
CODE
#include<bits/stdc++.h>
using namespace std;
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
const int N = 210;
int n,m,x,y,k;
bool a[N][N];
int d[N],s[N];
int dp[N][N][N];
int q[N<<1],head,tail;
int ans;
signed main(){
n=read,m=read,x=read,y=read,k=read;
char c;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
c=getchar();
a[i][j]=(c=='.'?0:1);
}
c=getchar();
}
for(int st,ed,i=1;i<=k;i++){
st=read,ed=read,d[i]=read;
s[i]=ed-st+1;
}
memset(dp,128,sizeof(dp));
for(int t=0;t<=k;t++) dp[x][y][t]=0;
for(int t=1;t<=k;t++){
if(d[t]==1){//shang
for(int j=1;j<=m;j++){
head=1,tail=0;
for(int i=n;i>=1;--i){
if(a[i][j]){head=1,tail=0;continue;}
while(head<=tail && q[head]>i+s[t]) head++;
dp[i][j][t]=max(dp[i][j][t],dp[i][j][t-1]);
if(head<=tail) dp[i][j][t]=max(dp[i][j][t],dp[q[head]][j][t-1]+q[head]-i);
while(head<=tail && dp[i][j][t-1]+i >= dp[q[tail]][j][t-1]+q[tail]) tail--;
q[++tail]=i;
ans=max(ans,dp[i][j][t]);
}
}
}
if(d[t]==2){//xia
for(int j=1;j<=m;j++){
head=1,tail=0;
for(int i=1;i<=n;i++){
if(a[i][j]){head=1,tail=0;continue;}
while(head<=tail && q[head]<i-s[t]) head++;
dp[i][j][t]=max(dp[i][j][t],dp[i][j][t-1]);
if(head<=tail) dp[i][j][t]=max(dp[i][j][t],dp[q[head]][j][t-1]+i-q[head]);
while(head<=tail && dp[i][j][t-1]-i >= dp[q[tail]][j][t-1]-q[tail]) tail--;
q[++tail]=i;
ans=max(ans,dp[i][j][t]);
}
}
}
if(d[t]==3){//zuo
for(int i=1;i<=n;i++){
head=1,tail=0;
for(int j=m;j>=1;--j){
if(a[i][j]){head=1,tail=0;continue;}
while(head<=tail && q[head]>j+s[t]) head++;
dp[i][j][t]=max(dp[i][j][t],dp[i][j][t-1]);
if(head<=tail) dp[i][j][t]=max(dp[i][j][t],dp[i][q[head]][t-1]+q[head]-j);
while(head<=tail && dp[i][j][t-1]+j >= dp[i][q[tail]][t-1]+q[tail]) tail--;
q[++tail]=j;
ans=max(ans,dp[i][j][t]);
}
}
}
if(d[t]==4){//you
for(int i=1;i<=n;i++){
head=1,tail=0;
for(int j=1;j<=m;j++){
if(a[i][j]){head=1,tail=0;continue;}
while(head<=tail && q[head]<j-s[t]) head++;
dp[i][j][t]=max(dp[i][j][t],dp[i][j][t-1]);
if(head<=tail) dp[i][j][t]=max(dp[i][j][t],dp[i][q[head]][t-1]+j-q[head]);
while(head<=tail && dp[i][j][t-1]-j >= dp[i][q[tail]][t-1]-q[tail]) tail--;
q[++tail]=j;
ans=max(ans,dp[i][j][t]);
}
}
}
}
write(ans);
return 0;
}
\(\tt{7.8}\) 模拟赛
\(T_1\) 分糖果
考虑对所有小朋友的糖数先对3取模，加和是3的倍数的情况只有4种 0 1 2、0 0 0、1 1 1、2 2 2。发现 0 1 2 超过3组就无意义，可以分成另外三种，所以枚举 0 1 2 的个数统计答案即可。
CODE
#include<bits/stdc++.h>
using namespace std;
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
const int N = 1e5+10;
int n;
int a[N];
int cnt[4];
int ans1;//2 1 0
int s[3][N],top[3];
signed main(){
n=read;
for(int i=1;i<=n;i++){
a[i]=read,a[i]%=3;
cnt[a[i]]++;
s[a[i]][++top[a[i]]]=i;
}
int d=min(cnt[0],min(cnt[1],cnt[2]));
int ans=0;
for(int i=0;i<=min(d,2);i++){
if(ans<i+(cnt[0]-i)/3+(cnt[1]-i)/3+(cnt[2]-i)/3)
ans=i+(cnt[0]-i)/3+(cnt[1]-i)/3+(cnt[2]-i)/3,ans1=i;
}
write(ans);pt;
cnt[0]-=ans1,cnt[1]-=ans1,cnt[2]-=ans1;
for(int i=1;i<=ans1;i++){
write(s[2][top[2]--]);putchar(' ');
write(s[1][top[1]--]);putchar(' ');
write(s[0][top[0]--]);pt;
}
for(int k=0;k<=2;k++)
for(int i=1;i<=cnt[k]/3;i++){
for(int j=1;j<=3;j++)
write(s[k][top[k]--]),putchar(' ');
pt;
}
return 0;
}
\(T_4\) 跳舞
赛时打了一个多小时，由于 \(n\leq 500\)，肆意预处理，优化了两次假做法，最后发现做法不可再优化，就交上了，不过 \(n\) 不大的时候随机数据也不好卡，出题人估计也想不到我这种逆天做法。
-
\(30pts\)
- 考虑预处理 \(g_{i,j}\) 表示 \(a_i\) 和 \(a_j\) 是否满足不互质。从左往右枚举 \(i\)，令 \(j\) 为 \(i\) 的下一位，如果 \(g_{i,j}=1\)，这两位可以消，那么消去哪一位可以使走的人尽可能多，就是本题重点。考虑设 \(num_i\) 为 \(a_i\) 在序列里能消去的个数，留下 \(num\) 较大的。然而这显然假，因为存在断点，比如
2 4 1 6 15 5 25，对于 6 和 15，虽然整个序列里，\(num_4>num_5\)，但是 6 和 4、2这辈子都不会到一块，所以我们要根据断点分块，在每块里求 \(num_i\)，这样就对了。但是对于断点的处理，我只处理了单个断点，而像2 4 8 7 49 12 15 5 25这种，7 49两个数组成了一个断点，也可以7 49 343组成一个断点，这样就不好判了，于是果断放弃。
CODE
#include<bits/stdc++.h> using namespace std; #define read read() #define pt puts("") inline int read{ int x=0,f=1;char c=getchar(); while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar(); return f*x; } void write(int x){ if(x<0) putchar('-'),x=-x; if(x>9) write(x/10); putchar(x%10+'0'); return; } const int N = 510; int n; int a[N]; int num[N]; bool can[N]; bool f[N][N]; int nxt[N],pre[N]; bool go[N]; int gcd(int x,int y){ if(!y) return x; return gcd(y,x%y); } int L[N],R[N],tot; int ans; bool cut[N]; set<int>bp;//break points signed main(){ n=read; for(int i=1;i<=n;i++) a[i]=read; for(int i=1;i<=n;i++){ pre[i]=i-1,nxt[i]=i+1; } bp.insert(0);bp.insert(n+1); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){ if(gcd(a[i],a[j])>1) f[i][j]=1; } while(1){ bool b=0; memset(can,0,sizeof(can)); set<int> :: iterator l,r; l=r=bp.begin();r++; for(;r != bp.end();l++,r++){ for(int i=*l+1;i<=*r-1;i++) for(int j=*l+1;j<=*r-1;j++){ if(i==j) continue; if(f[i][j]) can[i]=can[j]=1; } } for(int i=1;i<=n;i++) if(!can[i] && !cut[i]) cut[i]=1,bp.insert(i),b=1; if(!b) break; } set<int>::iterator l,r; l=r=bp.begin();r++; for(;r!= bp.end();l++,r++){ L[++tot]=*l+1; R[tot]=*r-1; } for(int t=1;t<=tot;t++) for(int i=L[t];i<=R[t];i++) for(int j=L[t];j<=R[t];j++) if(f[i][j]) num[i]++,num[j]++; while(1){ bool b=0; for(int t=1;t<=n;t++){ for(int i=L[t];i<=R[t];i++){ if(go[i]) continue; int j=nxt[i]; if(j>R[t]) break; if(f[i][j]){ b=1;ans++; if(num[i]<num[j]){ go[i]=1; nxt[pre[i]]=j; pre[j]=pre[i]; } else{ go[j]=1; nxt[i]=nxt[j]; pre[nxt[j]]=i; } } } } if(!b) break; } write(ans); return 0; } - 考虑预处理 \(g_{i,j}\) 表示 \(a_i\) 和 \(a_j\) 是否满足不互质。从左往右枚举 \(i\)，令 \(j\) 为 \(i\) 的下一位，如果 \(g_{i,j}=1\)，这两位可以消，那么消去哪一位可以使走的人尽可能多，就是本题重点。考虑设 \(num_i\) 为 \(a_i\) 在序列里能消去的个数，留下 \(num\) 较大的。然而这显然假，因为存在断点，比如
-
\(100pts\) 正解
- 同样处理 \(g\) 数组，然后考虑处理一个 \(c_{i,j}\) 表示 \([i,j]\) 是否可以全部回家。考虑转移：
\[c_{i,j}=c_{i,k-1} \& c_{k+1,j} \& (g_{k,i-1} | g_{k,j+1}) \]- 注意初始值，空区间 \((l>r)\) 也要赋为 \(1\)，同时注意边界。否则会被
3 8 9 20 18这样的数据 \(\text{Hack}\)。注意区间 DP，先枚举区间长度。 - 接下来考虑 \(dp_i\) 为到第 \(i\) 位并留下 \(i\)，然后转移显然：
\[dp_i=\max(dp_i,dp_j+((i-1)-(j+1)+1)\times c_{j+1,i-1}) \]- 注意 \(j\in [0,i-1]\)，最后答案即为 \(dp_{n+1}\)
- 以下是一些题外话，不过也有一些关系：
- 开始我枚举 \(j\in [1,i-1]\)，最后答案取了 \(dp_n\)，这显然是错的，不过数据过水放我过了，后来给别人调题时发现错误，便想往题库里加点 \(\text{Hack}\)，然后拍出来自己边界处理不当，没有处理 \(0\) 和 \(n+1\)，因此有了
3 8 9 20 18这组 \(\text{Hack}\)。后来我接着拍，好几万组都没有 \(\text{Hack}\) 掉 \(dp_n\) 的结果。然后我取 \(dp_{n+1}\)，令 \(j\in [1,i-1]\)，发现依然 \(\text{Hack}\) 不掉。 - 思索后发现，\(j\) 从 \(1\) 枚举，最后求 \(dp_{n+1}\) ，和 \(j\) 从 \(0\) 枚举，最后求 \(dp_{n}\) 都是和正确答案等价的，膜拜 \(master\) 的证明，毕竟最后至少剩下一个，可以钦定留下的是 \(1\) 或是 \(n\)。
- 开始我枚举 \(j\in [1,i-1]\)，最后答案取了 \(dp_n\)，这显然是错的，不过数据过水放我过了，后来给别人调题时发现错误，便想往题库里加点 \(\text{Hack}\)，然后拍出来自己边界处理不当，没有处理 \(0\) 和 \(n+1\)，因此有了
CODE
#include<bits/stdc++.h> using namespace std; #define read read() #define pt puts("") inline int read{ int x=0,f=1;char c=getchar(); while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar(); return f*x; } void write(int x){ if(x<0) putchar('-'),x=-x; if(x>9) write(x/10); putchar(x%10+'0'); return; } const int N = 510; int n; int a[N]; bool g[N][N]; int gcd(int x,int y){ if(!y) return x; return gcd(y,x%y); } bool can[N][N]; int dp[N]; signed main(){ n=read; for(int i=1;i<=n;i++) a[i]=read; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(gcd(a[i],a[j])>1) g[i][j]=1; for(int i=1;i<=n;i++) if(g[i-1][i] || g[i][i+1]) can[i][i]=1; for(int i=1;i<=n;i++) for(int j=1;j<i;j++) can[i][j]=1; for(int len=2;len<=n;len++){ for(int i=1;i+len-1<=n;i++){ int j=i+len-1; for(int k=i;k<=j;k++){ if(can[i][j]) break; bool c=can[i][k-1] & can [k+1][j] & (g[k][i-1] | g[k][j+1]); can[i][j]|=c; } } } dp[1]=0; for(int i=2;i<=n+1;i++) for(int j=0;j<=i-1;j++) dp[i]=max(dp[i],dp[j]+((i-1)-(j+1)+1)*can[j+1][i-1]); write(dp[n+1]); return 0; }
\(T_3\) 与或
赛时跳了，但是此题说实话并不难。首先分析一下，理论最大值应为先 & 再 |，因为显然有 \(x\&y | z\geq z \geq x|y\&z\)(不考虑优先级，从左向右)。那么得出最大值后，为了让字典序大，考虑将 \(|\) 前提，即对于一个位置 \(x\)，若填 | 后结果仍为理论最大值，那么这一位就填 |，后面仍然求理论最大值，即先 & 后 |。好像叫"按位贪心"。
- \(n^2\) 做法很好想，枚举每一位，\(O(n)\) 求结果判答案。
- \(n\times \log_2 n\) 做法，考虑在二进制每一位依次处理。具体的，将全序列分为三部分，一部分为处理完部分 \(A\)，另一部分为全是
&连接的部分 \(B\)，以及剩下的|连接的部分 \(C\)，由于连接处均为|，答案为 \(A|B|C\)。但是|和&之间并不满足结合律，因此要把 \(B\) 的首个拎出来，算入 \(A\) 中，即 \((A|a_x)\&B|C\) 才是对的。
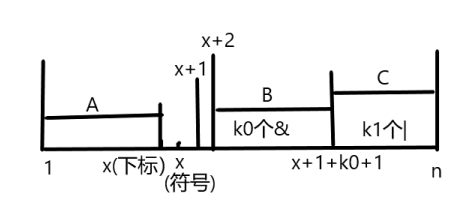
画图累死
- 对于 \(A,B,C\) 的处理，\(A\) 就是维护的答案。对于 \(B\)，就是说我们要算 \(a_l\&a_{l+1}\&\dots\&a_r\)，思考对二进制下每一位进行处理，考虑只有所有位都是 \(1\)，处理结果才是 \(1\)。对于 \(C\)，同理，但是每一位有至少一位为 \(1\) 就可以使结果对应位为 \(1\)，直接前缀和维护 \(1\) 的个数即可。
CODE
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
const int N = 2e5+10;
int n,k0,k1;
int ans,a[N];
int s[N];//0->& 1->|
int sum[N][62];
int lgx,maxx;
int A,B,C;
int calc_B(int l,int r){
int res=0;
for(int j=0;j<=lgx;j++)
if(sum[r][j]-sum[l-1][j]==r-l+1) res|=1ll<<j;
return res;
}
int calc_C(int l,int r){
int res=0;
for(int j=0;j<=lgx;j++)
if(sum[r][j]-sum[l-1][j]>0) res|=1ll<<j;
return res;
}
int check(int x){
B=calc_B(x+2,x+1+k0);
C=calc_C(x+1+k0+1,n);
return ((A|a[x+1])&B|C);
}
signed main(){
n=read,k1=read;
k0=n-k1-1;
for(int i=1;i<=n;i++) a[i]=read,maxx=max(maxx,a[i]);
lgx=log2(maxx)+1;
for(int i=1;i<=n;i++){
for(int j=0;j<=lgx;j++){
sum[i][j]=sum[i-1][j]+((a[i]>>j)&1);
}
}
A=a[1];
ans=check(0);
cout<<ans;pt;
for(int i=1;i<=n-1;i++){
if(!k1){
while(k0-->0) putchar('&');
break;
}
if(!k0){
while(k1-->0) putchar('|');
break;
}
if(check(i)==ans){
putchar('|');
k1--;
A=A|a[i+1];
}
else{
putchar('&');
k0--;
A=A&a[i+1];
}
}
return 0;
}
数据结构优化 DP
这类 DP 相对简单，推出来暴力式子之后选取合适的数据结构即可。
The Battle of Chibi 赤壁之战
求长度为 \(m\) 的上升子序列数量。
先考虑朴素 DP，设 \(dp_{i,j}\) 为处理到第 \(i\) 位并以 \(i\) 结尾，长度为 \(j\) 的上升子序列数量，有：
\[dp_{i,j}=\sum _{k=1}^{i-1} [a_k<a_i] dp_{k,j-1}
\]
显然二维偏序，树状数组维护即可。
CODE
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
#define lowbit(i) (i&(-i))
const int N = 1010;
const int p = 1e9+7;
int dp[N][N];
int n,m;
int a[N];
int t[N],num;
int tr[N];
int stamp[N];
int tt;
void add(int x,int k){
for(int i=x;i<=num;i+=lowbit(i))
tr[i]=(tr[i]+k)%p;
}
int query(int x){
int res=0;
for(int i=x;i>0;i-=lowbit(i))
res=(res+tr[i])%p;
return res;
}
signed main(){
int T=read;
for(int _=1;_<=T;_++){
int ans=0;
memset(dp,0,sizeof(dp));
n=read,m=read;
for(int i=1;i<=n;i++) t[i]=a[i]=read;
sort(t+1,t+n+1);
num=unique(t+1,t+n+1)-t-1;
for(int i=1;i<=n;i++) a[i]=lower_bound(t+1,t+num+1,a[i])-t;
for(int i=1;i<=n;i++)
dp[i][1]=1;
for(int j=2;j<=m;j++){
for(int i=j-1;i<=n;i++){
dp[i][j]=query(a[i]-1)%p;//注意是a[i]-1
add(a[i],dp[i][j-1]);
}
memset(tr,0,sizeof(tr));
}
for(int i=m;i<=n;i++) ans=(ans+dp[i][m])%p;
printf("Case #%lld: ",_);write(ans);pt;
}
return 0;
}
倍增优化 DP
难题，都不会。 大体用于可以任意划分的问题上，然后进行二进制拆分试填。
[NOIP2012 提高组]开车旅行
对于本题，显然天数是任意划分的。
- 预处理 \(ga_i,gb_i\) 分别表示小 \(A\) 和 小 \(B\) 在城市 \(i\) 时的下一个目的地，可用 \(set\) 实现(破防，预处理这个我调了近 \(1h\)，包括学习 \(set\) 用法……)。
- 处理 \(dp_{i,j,k}\) 表示 \(k\) 先开车，从 \(j\) 出发，开了 \(2^i\) 天到达的城市。
- 处理 \(da_{i,j,k}\) 表示 \(k\) 先开车，从 \(j\) 出发，开了 \(2^i\) 天 \(A\) 行驶的公里数。
- 处理 \(db_{i,j,k}\) 表示 \(k\) 先开车，从 \(j\) 出发，开了 \(2^i\) 天 \(B\) 行驶的公里数。
转移方程见代码吧，注意分讨 \(i=1\) 和 \(i>1\)。
对于第一问，枚举每个城市，考虑从 \(\log\) 试填(类似与倍增求LCA，毕竟都是倍增思想)，分别计算 \(resa,resb\)，求解比值即可。
第二问与第一问同理。
服了，set预处理ga,gb卡我时间最久。
CODE
#include<bits/stdc++.h>
using namespace std;
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
#define pii pair<int,int>
#define mp std::make_pair
const int N = 1e5+10;
int n,m;
long long h[N];
int ga[N],gb[N];
void init(){
set< pii > s;
h[0]=-2e9-1e8;h[n+1]=2e9+1e8;
set < pii > :: iterator it1,it2,it3;
s.insert(mp(h[n+1],n+1));
s.insert(mp(h[n],n));
s.insert(mp(h[n-1],n-1));
gb[n-1]=n;
for(int i=n-2;i>=1;--i){
it1=it2=s.upper_bound(mp(h[i],i));
it1--;
int pre1=(*it1).second;
int nxt1=(*it2).second;
it1--;it2++;
int pre2=(*it1).second;
int nxt2=(*it2).second;
if(h[i]-h[pre1]<=h[nxt1]-h[i] && pre1){
gb[i]=pre1;
ga[i]=(h[i]-h[pre2]<=h[nxt1]-h[i])?pre2:nxt1;
}
else{
gb[i]=nxt1;
ga[i]=(h[i]-h[pre1]<=h[nxt2]-h[i])?pre1:nxt2;
}
s.insert(mp(h[i],i));
}
}
int dp[25][N][2];
int da[25][N][2],db[25][N][2];
int ans1;double r=1e9;
signed main(){
n=read;
for(int i=1;i<=n;i++) h[i]=read;
init();
for(int j=1;j<=n;j++){
dp[0][j][0]=ga[j];
dp[0][j][1]=gb[j];
}
for(int j=1;j<=n;j++)
for(int k=0;k<=1;k++)
dp[1][j][k]=dp[0][dp[0][j][k]][k^1];
for(int i=2;i<=20;i++){
for(int j=1;j<=n;j++){
for(int k=0;k<=1;k++)
dp[i][j][k]=dp[i-1][dp[i-1][j][k]][k];
}
}
for(int j=1;j<=n;j++){
if(ga[j])
da[0][j][0]=abs(h[j]-h[ga[j]]);da[0][j][1]=0;
if(gb[j])
db[0][j][1]=abs(h[j]-h[gb[j]]);db[0][j][0]=0;
}
for(int j=1;j<=n;j++){
for(int k=0;k<=1;k++){
da[1][j][k]=da[0][j][k]+da[0][dp[0][j][k]][k^1];
db[1][j][k]=db[0][j][k]+db[0][dp[0][j][k]][k^1];
}
}
for(int i=2;i<=20;i++){
for(int j=1;j<=n;j++){
for(int k=0;k<=1;k++){
da[i][j][k]=da[i-1][j][k]+da[i-1][dp[i-1][j][k]][k];
db[i][j][k]=db[i-1][j][k]+db[i-1][dp[i-1][j][k]][k];
}
}
}
int x0=read;
for(int s=1;s<=n;s++){
int p=s,x=x0;
int resa=0,resb=0;
for(int k=18;k>=0;--k){
if(!dp[k][p][0]) continue;
if(x0>=resa+resb+da[k][p][0]+db[k][p][0]){
resa+=da[k][p][0];
resb+=db[k][p][0];
p=dp[k][p][0];
}
}
if(resb!=0){
double res=resa*1.0/resb;
if(res==r) ans1=h[s]>h[ans1]?s:ans1;
if(res<r) ans1=s,r=res;
}
}
write(ans1);pt;
for(m=read;m;--m){
int s=read,x=read;
int res1=0,res2=0;
for(int k=18;k>=0;--k){
if(!dp[k][s][0]) continue;
if(x>=res1+res2+da[k][s][0]+db[k][s][0]){
res1+=da[k][s][0];
res2+=db[k][s][0];
s=dp[k][s][0];
}
}
write(res1);putchar(' ');write(res2);pt;
}
return 0;
}
Count The Repetitions
考虑答案是满足 \(\text{conn}(s2,n2\times m)\) 能由 \(\text{conn}(s1,n1)\) 生成，最大的 \(m\)。
设 \(dp_{i,j}\) 为从 \(s1_i\) 开始拼，拼 \(2^j\) 个 \(s2\) 需要的字符数。
\[dp_{i,j}=dp_{i,j-1}+dp_{i+dp_{i,j-1}\%l1,j-1}
\]
接下来，从 \(\log\) 试填即可。
感觉倍增优化不是很好想，但是知道是倍增优化之后就挺好做了。
CODE
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
char s1[110],s2[110];
int n1,n2;
int dp[110][35];
int l1,l2;
int m;
signed main(){
while(cin>>(s2+1)>>n2>>(s1+1)>>n1){
l1=strlen(s1+1),l2=strlen(s2+1);
m=0;
memset(dp,0,sizeof(dp));
bool p=0;
for(int i=1;i<=l1;i++){
int j=1;
bool b=0;
for(int k=i;k<=l1 && j<=l2;k++){
if(s1[k]==s2[j]) j++,b=1;
dp[i][0]++;
}
while(j<=l2){
b=0;
for(int k=1;k<=l1 && j<=l2;k++){
if(s1[k]==s2[j]) j++,b=1;
dp[i][0]++;
}
if(!b) break;
}
if(!b) {p=1;break;}
}
if(p){putchar('0');pt;continue;}
for(int j=1;j<=30;j++){
for(int i=1;i<=l1;i++){
dp[i][j]=dp[i][j-1]+dp[(i+dp[i][j-1]-1)%l1+1][j-1];
}
}
int i=1;
for(int k=30;k>=0;--k){
if(n1*l1>=i+dp[(i-1)%l1+1][k]-1){
m+=(1ll<<k);
i+=dp[(i-1)%l1+1][k];
}
}
m=m/n2;
write(m);pt;
}
return 0;
}
斜率优化 DP
蓝书讲得很好，从三个"任务安排"一步步让我学会了斜率优化。(我真学会了吗)
任务安排
第一个朴素 \(n^2\) 暴力不再多说。
貌似谷上没有任务安排 \(2\)，题面都一样，就是 \(n\) 开到 \(3\times 10^5\)，只能思考 \(O(n)\) 做法。考虑换一种 DP 方式，设 \(dp_i\) 为前 \(i\) 项任务需要花费的最小系数，那么有：
\[dp_i=\min(dp_i,dp_j+T_i\times (C_i-C_j)+s\times (C_n-C_j))
\]
其中 \(T_i,C_i\) 都是前缀和。上式的意义是，枚举断点 \(j\)，使 \(j+1\sim i\) 划分为一组任务。我们考虑复杂度的瓶颈在于不知道有多少组任务即不知道会停留多少个 \(s\)，所以我们直接在这一位就加上后面 \(s\) 的贡献即可。
考虑均摊 \(O(1)\) 求上式。
\[\begin{aligned} dp_i &= \min(dp_j+T_i\times (C_i-C_j)+s\times (C_n-C_j)) \\ &= \min(dp_j+T_i\times C_i-T_i\times C_j+s\times C_n-s\times C_j) \\ &= \min(dp_j-T_i\times C_j-s\times C_j)+T_i\times C_i+s\times C_n \\ &= \min(dp_j-(T_i+s)\times C_j)+T_i\times C_i+s\times C_n \end{aligned}
\]
我们假设取到了一个最优决策 \(j\)，则必然有：
\[dp_i=dp_j-(T_i+s)\times C_j+T_i\times C_i+s\times C_n
\]
也就是：
\[dp_j=(T_i+s)\times C_j+dp_i-T_i\times C_i-s\times C_n
\]
我们发现含 \(j\) 的项有两个，即 \(dp_j\) 和 \(C_j\)，剩下的当做常数，就有形如 \(y=k\times x+b\) 的一次函数直线，其中 \(k=T_i+s,b=dp_i-T_i\times C_i-s\times C_n\)。考虑以 \(dp_j\) 为纵坐标，\(C_j\) 为横坐标建立平面直角坐标系，将 \(j\) 点表示到坐标系上。你会发现其实令 \(b\) 最小就会使 \(dp_i\) 最小，也就是说将一个斜率为 \(k=T_i+s\) 的直线从下向上平移，第一个接触到的 \(j\) 点即为最优决策点。
我们发现，一个下凸的 \(j_2\) 一定比上凸的 \(j_2\) 要更优。如下图。
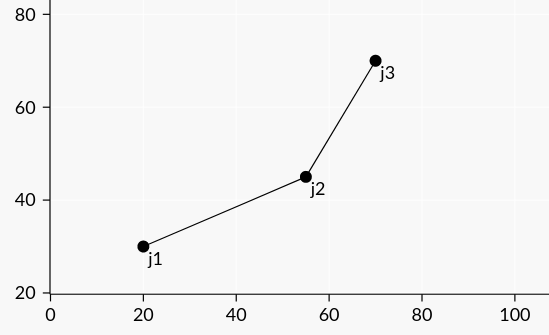
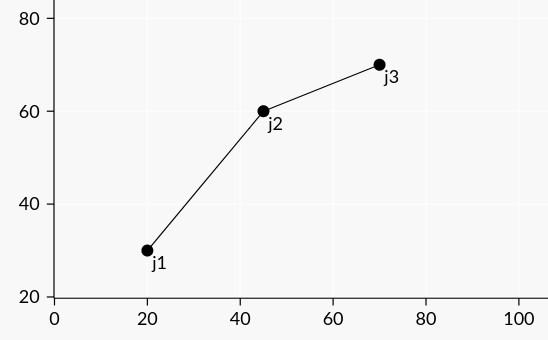
那么我们可以使用单调队列维护凸壳，在队尾入队时使其保持下凸状态，并且，由于直线的斜率是 \(T_i+s\) 单调递增，因此我们只要维护凸壳左下端点(即单调队列队首)，每次弹出斜率小于 \(T_i+s\) 的点，队首元素即为最优决策。
CODE
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
const int N = 3e5+10;
int n,s;
int t[N],T[N],c[N],C[N];
int dp[N];
int q[N<<1],head,tail;
signed main(){
n=read,s=read;
for(int i=1;i<=n;i++){
t[i]=read,T[i]=T[i-1]+t[i];
c[i]=read,C[i]=C[i-1]+c[i];
}
memset(dp,0x3f,sizeof(dp));
head=1,tail=0;
dp[0]=0;
q[++tail]=0;
for(int i=1;i<=n;i++){
while(head<tail && (dp[q[head]]-dp[q[head+1]])*1.0/(C[q[head]]-C[q[head+1]])<T[i]+s) head++;
dp[i]=dp[q[head]]-(T[i]+s)*C[q[head]]+T[i]*C[i]+s*C[n];
while(head<tail && (dp[q[tail]]-dp[q[tail-1]])*1.0/(C[q[tail]]-C[q[tail-1]])>=(dp[i]-dp[q[tail]])*1.0/(C[i]-C[q[tail]])) tail--;
q[++tail]=i;
}
write(dp[n]);
return 0;
}
[SDOI2012]任务安排
这是第三道，与前面不同的是，\(t\) 可能为负，所以斜率 \(k=T_i+s\) 不再单调。不单调也无所谓，我们发现下凸壳上的斜率是单调递增的，直线 \(y=(T_i+s)x+b\) 第一次接触到凸壳上的点 \(j_p\)，必然要满足 \(k(j_p,j_{p-1})<T_i+s<k(j_p,j_{p+1})\)，直接二分求出凸壳上第一个斜率大于 \(T_i+s\) 的点即为最优决策点。
CODE
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
const int N = 3e5+10;
int n,s;
int T[N],C[N];
int dp[N];
int tull[N],top;
double calc(int j,int k){
double a=(dp[j]-dp[k])*1.0;
if(!a) return 0;
double b=(C[j]-C[k])*1.0;
if(!b) return (a>0?1:-1)*1e18;
return a/b;
}
signed main(){
n=read,s=read;
for(int i=1,t,c;i<=n;i++){
t=read,c=read;
T[i]=T[i-1]+t,C[i]=C[i-1]+c;
}
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
tull[++top]=0;
for(int i=1;i<=n;i++){
int st=1,ed=top,j=tull[top];
if(top>1)
while(st<=ed){
int mid=(st+ed)>>1;
if(calc(tull[mid+1],tull[mid])>T[i]+s){
ed=mid-1;
j=tull[mid];
}
else st=mid+1;
}
dp[i]=dp[j]-(T[i]+s)*C[j]+T[i]*C[i]+s*C[n];
while(top>1 && calc(tull[top],tull[top-1])>=calc(i,tull[top])) top--;
tull[++top]=i;
}
write(dp[n]);
return 0;
}
Cats Transport
对于每只猫 \(i\)，我们定义一个 \(A_i\) 表示人最早从第几时刻出发才能接到第 \(i\) 只猫，容易有 \(A_i=T_i-\sum\limits _{j=1}^{h_i}D_j\)，那么此题就转化成与任务安排相似的问题了。将 \(A\) 排序保证单调性，并用 \(S\) 数组记录前缀和，方便转移。接着设 \(dp_{i,j}\) 表示前 \(i\) 个人带走 \(j\) 只猫的最小等待时间，令前 \(i-1\) 个人带走 \(k\) 只猫，那么第 \(i\) 个人就会带走 \(j-k\) 只猫，容易有：
\[dp_{i,j}=\min(dp_{i-1,k}+\sum_{p=k+1}^{j}A_j-A_p)
\]
套路推式子，显然 \(\sum\limits _{p=k+1}^{j}A_j-A_p=A_j\times(j-k)-(S_j-S_k)\)，然后钦定一个 \(j\) 使之最小化答案，去掉 \(\min\)，最终移项得：
\[dp_{i-1,k}+S_k=A_j\times k+dp_{i,j}-A_j\times j+S_j
\]
按照上面的套路，由于排序了所以斜率 \(k=A_j\) 单调递增，所以直接用任务安排2的方式一样单调队列维护凸壳即可。
CODE
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
const int N = 2e5+10;
int n,m,p;
int dis[N];
int h[N],t[N];
int A[N],S[N];
int dp[110][N];
int q[N<<1],head,tail;
double slope(int i,int x,int y){
double a=((dp[i-1][x]+S[x])-(dp[i-1][y]+S[y]))*1.0;
double b=x-y;
return a/b;
}
signed main(){
n=read,m=read,p=read;
for(int i=2,d;i<=n;i++) d=read,dis[i]=dis[i-1]+d;
for(int i=1;i<=m;i++) h[i]=read,t[i]=read;
for(int i=1;i<=m;i++){
A[i]=t[i]-dis[h[i]];
}
sort(A+1,A+m+1);
for(int i=1;i<=m;i++)
S[i]=S[i-1]+A[i];
memset(dp,0x3f,sizeof(dp));
for(int j=1;j<=m;j++){
dp[1][j]=A[j]*j-S[j];
}
for(int i=2;i<=p;i++){
dp[i][0]=0;
head=1,tail=0;
q[++tail]=0;
for(int j=1;j<=m;j++){
while(head<tail && slope(i,q[head+1],q[head])<=A[j]) head++;
int k=q[head];
dp[i][j]=dp[i-1][k]+S[k]-A[j]*k+A[j]*j-S[j];
while(head<tail && slope(i,q[tail],q[tail-1])>=slope(i,j,q[tail])) tail--;
q[++tail]=j;
}
}
write(dp[p][m]);
return 0;
}
\(\tt{7.12}\) 模拟赛
\(T_1\) 最短路
此题路径长定义为两点间边权和加上经过的点权最大值。被 \(T_1\) 薄纱了，好题，考察：
\(\text{Floyd}\) 的本质是什么？
我们学的 \(\text{Floyd}\)，是，这样的？
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(s[i][k]+s[k][j]<s[i][j])
s[i][j]=s[i][k]+s[k][j];
好吧，其实对这个东西并未理解的特别透彻。今天这个题让我对 \(\text{Floyd}\) 了解了更多。
未进行空间优化的 \(\text{Floyd}\)，是三维 \(DP\)，即 \(s_{k,i,j}\) 表示"中转点到 \(k\) "，\(i\) 到 \(j\) 的最短路，也就是 \(i\) 到 \(j\) 的路径上只经过 \(1\sim k\) 点的最短路径。然后可以滚掉第一维。这是 \(k\) 的实际意义。
对于此题，由于它要加上点的最大值，我们考虑给点权排序，那么当前枚举的 \(k\) 就一定是 \(i\) 到 \(j\) 路径上的最大点权，最大值即 \(\max(val_i,val_j,val_k)\)，最短边权和照常求，定义 \(s_{i,j}\) 为 \(i\)，\(j\) 间最短路，\(ans_{i,j}\) 为 \(i\) 到 \(j\) 间边权和加上经过的点权最大值的最小值，即答案。然后转移即可。
具体地，先排序，枚举 \(k\)，那么当前枚举的 \(k\) 就是路径上(不包含 \(i,j\) )权值最大的点，考虑用它更新答案。先更新最短路，接着用它更新 \(ans_{i,j}\)，此时的边权和最小值是 \(s_{i,j}\)，点权最大值为 \(\max(val_i,val_j,val_k)\)。直接更新即可。
CODE
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
const int N = 305;
int n,m,q;
int s[N][N];
int ans[N][N],val[N];
int fa[N];
int find(int x){return (fa[x]==x)?x:find(fa[x]);}
pair<int,int>K[N];
#define mp std::make_pair
void Floyd(){
for(int l=1;l<=n;l++){
int k=K[l].second;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
s[i][j]=min(s[i][j],s[i][k]+s[k][j]);
ans[i][j]=min(ans[i][j],s[i][j]+max(max(val[i],val[j]),val[k]));
}
}
}
signed main(){
freopen("path.in","r",stdin);
freopen("path.out","w",stdout);
n=read,m=read,q=read;
memset(s,0x3f,sizeof(s));
memset(ans,0x3f,sizeof(ans));
for(int i=1;i<=n;i++) val[i]=read,K[i]=mp(val[i],i);
sort(K+1,K+n+1);
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1,a,b,c;i<=m;i++){
a=read,b=read,c=read;
s[a][b]=s[b][a]=min(s[a][b],c);
int Fa=find(a),Fb=find(b);
if(Fa!=Fb) fa[Fb]=Fa;
}
Floyd();
for(int u,v;q;--q){
u=read,v=read;
int Fu=find(u),Fv=find(v);
if(Fu!=Fv) puts("-1");
else write(ans[u][v]),pt;
}
return 0;
}
所以，\(\text{Floyd}\) 的本质是什么？
\(T_4\) 树
简单题，但是只得了 \(25pts\)，死因是看出来根号分治但是只会一半……
首先，这个题对我很友好，最后答案是确定的，不是求什么最大值最小值，这就很好，按照题意模拟即可。
考虑处理第 \(i\) 次从 \(b_i\) 转移到 \(b_{i+1}\)，此时步长为 \(c_i\)。考虑倍增，求 \(\tt{LCA}\)，二进制拆分往上跳(当然倍增求 \(\tt{LCA}\) 比树剖等慢，不过此题的复杂度瓶颈显然不在 \(n\times \log _2 n\) 的求 \(\tt{LCA}\))。将 \(c_i\) 拆二进制倍增上跳，这样的话复杂度为 \(O(n\times \log _2 n+\sum\limits _{i=1}^{n-1}\dfrac{n}{c_i}\times \log_2 c_i)\)。发现复杂度瓶颈就在于 \(\sum \dfrac{n}{c_i}\)，发现如果步长很小就会被卡成 \(O(n^2)\)，祭。考虑根号分治，$c_i> \sqrt{n} $ 显然直接二进制拆分然后倍增填数，但是 \(c_i<\sqrt{n}\) 赛时就不会处理了，只得硬着头皮交上暴力，喜提 \(25pts\)。
\(c_i<\sqrt{n}\) 时，考虑一共最多只有 \(\sqrt{n}\) 种步长，直接暴力处理每种步长的情况，类似前缀和，然后 \(sum_u+sum_v-2\times sum_{lca}\) 的思想处理，注意，我们只用思想，具体式子大不相同。
具体地，维护一个 \(sum_{c,x}\) 表示当前步长为 \(c\)，从 \(x\) 节点上跳到根节点停留的所有点的权值和。这，赛时想到了，但是不会处理……那就假装我们处理好了，那么从 \(u\) 上跳贡献即为 \(sum_{c,u}\)，\(v\) 即 \(sum_{c,v}\)。接下来考虑减去从根节点到 \(lca\) 的贡献，赛后改的时候唐唐唐，减去 \(2\times sum_{c,lca}\)。这显然不对，考虑从 \(u\) 上跳到 \(lca\) 需要 \(dep_u-dep_{lca}\) 步，令 \(r=(dep_u-dep_{lca})\mod c\)，则第一个多余贡献出在 \(lca\) 的 \(c-r\) 级祖先处，答案显然要减去 \(sum_{c,Fa(lca,c-r)}\)。\(v\) 同理。注意特判 \(lca\) 处即 \(r=0\) 即可。
最后一个问题就是处理 \(sum\) 数组了，考虑对于每个 \(c_i\)，我们跑一遍 \(\tt{DFS}\)，对于每个点 \(x\)，设 \(Fa(x,k)\) 表示 \(x\) 的 \(k\) 级祖先，这个也是直接倍增二进制试填就可以 \(\log\) 求出。那么 \(x\) 一定上跳到 \(Fa(x,c)\) 处，即 \(x\) 应从 \(Fa(x,c)\) 转移来，有 \(sum_{c,x}=sum_{c,Fa(x,c)}+a_x\)。单次预处理 \(O(n\times \log _2 n)\)，最多处理 \(\sqrt{n}\) 次，预处理总复杂度 \(O(n\times \log _2 n\times \sqrt{n})\)。
总复杂度 \(O(n\times \log _2 n \times \sqrt{n})\)。
CODE
#include<bits/stdc++.h>
using namespace std;
#define read read()
#define pt puts("")
inline int read{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
const int N = 50010;
int n;
int a[N],b[N],c[N];
struct EDGE{int next,to;}e[N<<1];
int head[N],total;
void add(int u,int v){e[++total]={head[u],v};head[u]=total;}
int depth[N];
int fa[N][20];
int lg2[N];
int siz[N],wson[N];
int top[N];
void dfs1(int x){
depth[x]=depth[fa[x][0]]+1;
siz[x]=1;
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(y==fa[x][0]) continue;
fa[y][0]=x;
dfs1(y);
if(siz[y]>siz[wson[x]]) wson[x]=y;
siz[x]+=siz[y];
}
}
void dfs2(int x,int tp){
top[x]=tp;
if(wson[x]) dfs2(wson[x],tp);
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(y==wson[x]||y==fa[x][0]) continue;
dfs2(y,y);
}
}
void init(){
for(int i=2;i<=n;i++) lg2[i]=lg2[i>>1]+1;
for(int j=1;j<=lg2[n];j++)
for(int i=1;i<=n;i++)
fa[i][j]=fa[fa[i][j-1]][j-1];
}
int LCA(int u,int v){
while(top[u]!=top[v]){
if(depth[top[u]]<depth[top[v]]) swap(u,v);
u=fa[top[u]][0];
}
return (depth[u]<depth[v]?u:v);
}
int sum[250][N];
int FA(int x,int k){
int res=x;
for(int i=lg2[k];i>=0;i--){
if(depth[x]-depth[fa[res][i]]<=k) res=fa[res][i];
}
return res;
}
void dfs(int x,int c){
if(depth[x]>c) sum[c][x]=sum[c][FA(x,c)]+a[x];
else sum[c][x]=a[x];
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(y==fa[x][0]) continue;
dfs(y,c);
}
}
int ans;
signed main(){
n=read;
for(int i=1;i<=n;i++) a[i]=read;
for(int i=1,a,b;i<n;i++){
a=read,b=read;
add(a,b),add(b,a);
}
dfs1(1);dfs2(1,1);
init();
for(int i=1;i<=n;i++) b[i]=read;
for(int i=1;i<=n-1;i++) c[i]=read;
for(int i=1;i<=n-1;i++)
if(c[i]<=sqrt(n))
if(!sum[c[i]][1]) dfs(1,c[i]);
for(int i=1;i<=n-1;i++){
int u=b[i],v=b[i+1];
int lca=LCA(u,v);
ans=0;
if(c[i]<=sqrt(n)){
ans+=sum[c[i]][u]+sum[c[i]][v];
int r1=(depth[u]-depth[lca])%c[i];
int r2=(depth[v]-depth[lca])%c[i];
if(!r1) ans=ans-sum[c[i]][lca]*2+a[lca];
else ans=ans-sum[c[i]][FA(lca,c[i]-r1)]-sum[c[i]][FA(lca,c[i]-r2)];
}
else{
while(depth[u]>=depth[lca]){
ans+=a[u];
u=FA(u,c[i]);
}
while(depth[v]>depth[lca]){
ans+=a[v];
v=FA(v,c[i]);
}
}
write(ans);pt;
}
return 0;
}
闲话
\([2024.7.6]\)
上午全机房组队打衬衫比赛，\(T_A\) 分配给我，\(4 mins\) 切了，然后几个人研究 \(T_B\) 打表，夹子哥充分展现其毅力，\(78\) 发罚时拿下……不过最后十几个人也没抽着衬衫。
\([2024.7.8]\)
下午打 \(\text{csp-j}\) 模拟赛，真· \(\text{csp-j}\)，\(T_1\) 打了逆天错解挂 \(5\) 分，后来几人为了卡xrlong，逆天造数据卡成 \(40\) 分。\(T_2\) 暴力写假了，只骗得 \(5\) 分。 \(T_3\) 跳了，\(T_4\) 逆天骗分水得 \(30\) 高分。模拟赛不知是谁出的，主角是zwh，乐。
\([2024.7.9]\)
今天上午讨论过于混乱被 \(huge\) \(D\) 了，甚至出了一个时间安排表，什么时候 "沉浸式刷题"，什么时候"允许讨论"……
中午看《拿破仑传》时看到一句话：
展望未来，我只看到光明。 即使没有光明，人也得活在现实里，勇敢者蔑视未来。 ——因为他蔑视未来，未来为他所用。
\([2024.7.10]\)
上午打模拟赛，\(20mins\) 切 \(T_1\)，然后看了看 \(T_2,T_3,T_4\)，发现 \(T_4\) 相对好写，狂写不止，但是质疑 \(n^2\) 的复杂度，果断改成 \(n\times \log_2^2 n\) 的线段树上跑二分。结果调了一个多小时还没调出来，最后发现暴力代码 \(A\) 了，而线段树挂了 \(16pts\)。赛后发现其实有 \(n\times \log_2 n\) 的简单做法，难绷。
中午给爹打电话，想让我退赛，称对眼伤害太大。确实，一天近十二个小时的奥赛时间，右眼已经近九百度了，我真赌不起啊，但是这样退掉又确实不甘心，纠结。
晚上去衡中书店买了本《资本论》。盗版书籍。劣质纸张，一看书后面，还说是 "专家浓缩"，无语，我用你浓缩？
\([2024.7.11]\)
上午打模拟赛，大概是最后一场，啥也不会。写了退赛申请。
下午三点，向 \(miaomiao\) 递交了退赛申请。无奈，但愿一切都是最好的安排。正式 AFO。
晚上出了中考录取结果。
\([2024.7.12]\)
上午又打模拟赛，这回真是最后一场了。还行,应该 \(T_1,T_2,T_4\) 都能骗到点分。\(80+85+25=190\)，喜提 \(\tt{Rank5}\)。考的最好的一集……
安静
只剩下钢琴陪我谈了一天
睡着的大提琴 安静的旧旧的
我想你已表现的非常明白
我懂我也知道 你没有舍不得
你说你也会难过我不相信
牵着你陪着我 也只是曾经
希望他是真的比我还要爱你
我才会逼自己离开
你要我说多难堪? 我根本不想分开
为什么还要我用微笑来带过?
我没有这种天份 包容你也接受他
不用担心的太多 我会一直好好过
你已经远远离开 我也会慢慢走开
为什么我连分开都迁就着你?
我真的没有天份 安静的没这么快
我会学着放弃你 是因为我太爱你
只剩下钢琴陪我谈了一天
睡着的大提琴 安静的旧旧的
我想你已表现的非常明白
我懂我也知道 你没有舍不得
你说你也会难过我不相信
牵着你陪着我 也只是曾经
希望他是真的比我还要爱你
我才会逼自己离开
你要我说多难堪? 我根本不想分开
为什么还要我用微笑来带过?
我没有这种天份 包容你也接受他
不用担心的太多 我会一直好好过
你已经远远离开 我也会慢慢走开
为什么我连分开都迁就着你?
我真的没有天份 安静的没这么快
我会学着放弃你 是因为我太爱你
你要我说多难堪? 我根本不想分开
为什么还要我用微笑来带过?
我没有这種天份 包容你也接受他
不用担心的太多 我会一直好好过
你已经远远离开 我也会慢慢走开
为什么我连分开都迁就着你?
我真的没有天份 安静的没这么快
我会学着放弃你 是因为我太爱你
乐，明天还有模拟赛，考完才放假，所以今天的模拟赛仍然不是最后一场……
