CF1037H Security
\(CF1037H\ \ Security\)
题意
给定一个母串 \(s\) 和 \(T\) 次询问，每次询问 \(S[l\dots r]\) 中字典序严格大于 \(t\) 的最小串，没有则输出 \(-1\)
思路分析
不会,不分析了，贺了
首先，因为这个题的标签里有SAM，所以我们要用SAM
壹
首先我们考虑无 \(l,r\) 限制，很明显将 \(t\) 在母串 \(s\) 的 \(SAM\) 上跑。设答案串为 \(ans\)， \(ans\) 与 \(t\) 匹配位数为 \(i\) 位(\(ans\) 与 \(t\) 前 \(i\) 位相同)，那么一定有：
-
\(ans[i+1] > t[i+1]\)
-
在满足 \(1\) 时令 \(i\) 最大，\(ans[i+1]\) 最小
贰
此题难点就在于高贵的 \([l,r]\) 限制，除了满足上面两条，还有：
- 串 \(ans\) 包含于 \([l,r]\)，此时 \(ans\) 的 \(endpos\) 要介于 \([l+len_{ans}\ ,\ r]\) 之间，我们只要 \(judge\) 每个 \(ans\) 即可
问题来了，如何 \(judge ?\)
首先考虑一个推论：
推论：对于后缀树上的某节点 \(u\)，他的 \(endpos\) 集合为其子树的并集，即：
\[endpos(u)=\bigcup_{v\in son[u]} endpos(v) \]当然，我们还应加上以 \(u\) 结尾的最长子串的 \(endpos\)
证明：
什么都证明只会害了你。 ——\(Shadow\)
开玩笑的
对于两个子串 \(S1,S2\)，若 \(|S1|<|S2|\) ，且 \(S1\) 是 \(S2\) 的后缀，就必然有
\[endpos(s1)\varsubsetneq endpos(s2) \]
这个结论熟悉吧，最开始学 \(SAM\) 的时候，这是某个引理。那么根据后缀树后缀链接的定义，\(S_u\) 一定是 \(S_v\) 的后缀 \((v\in son[u])\)，那么推论显然得证。
这样描述不太直观 很不直观可以画画图，比如串 "\(spxssspxx\)" (不要管 spx 是谁)，我们构建出它的 \(SAM\)，写出所有子串，如图：
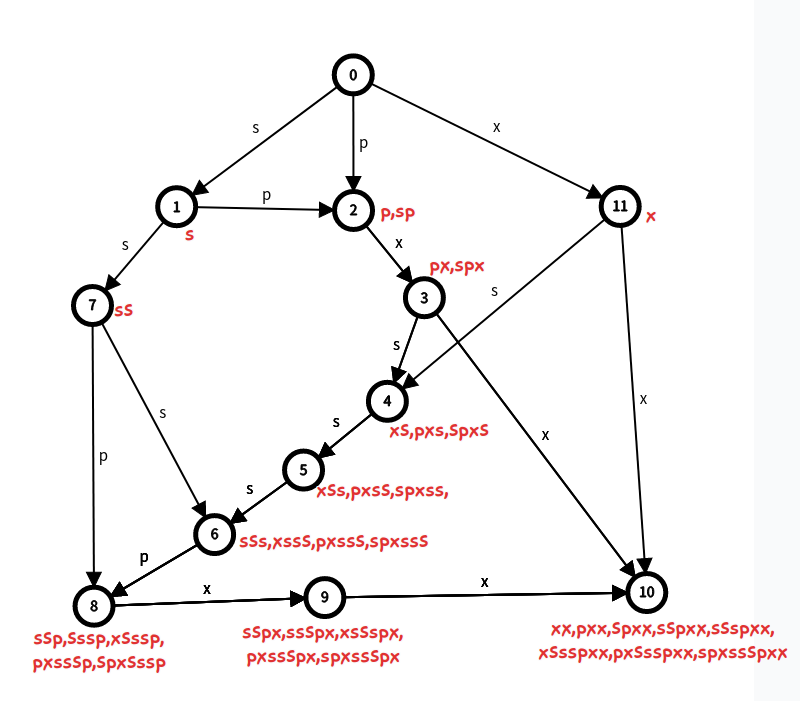
其后缀树长这个样子
.png)
那么我们再耐心地标出每个节点的 \(endpos\) 集合，就成了这个样子：
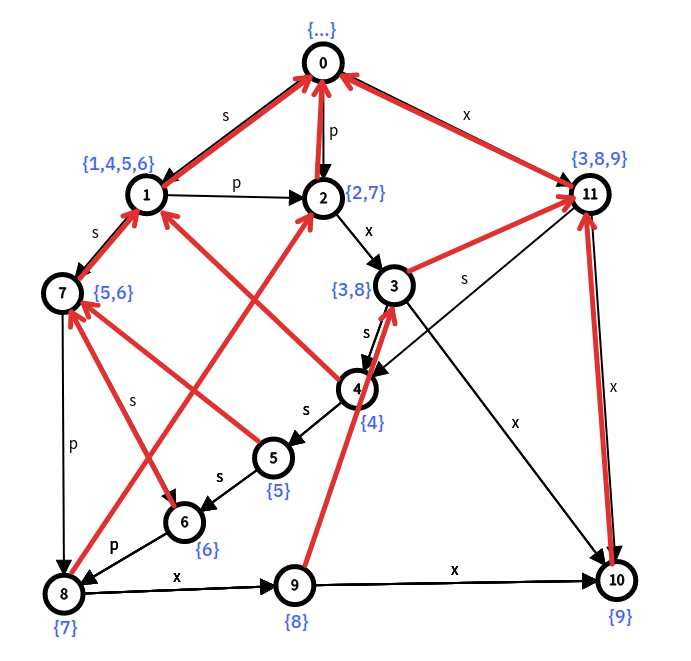
好了，那么到此就差不多了，上文因我语文功底有限，叙述可能不太清楚，所以——
领会精神吧~！
好，对于具体的实现，我们让每个节点只保留最长串(即从根节点到它的最长路径)的 \(endpos\)，然后对于一个非叶节点，我们通过线段树合并来求解它的 \(endpos\) 集合，最后 \(judge\) 是否存在 \([l+i-1,r]\) 内的 \(endpos\) 即可。
\(AC\ \ code\)
#include<bits/stdc++.h>
using namespace std;
#define read read()
#define pt puts("")
inline int read
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+c-'0',c=getchar();
return f*x;
}
void write(int x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
return;
}
#define N 200010
int n,m;
char s[N];
int len[N<<1],link[N<<1];
int ch[N<<1][27];
vector<int >son[N<<1];
int tot,last;
int ans[N<<1];
int siz;
int root[N<<5];
int ls[N<<5],rs[N<<5];
void add(int &rt,int l,int r,int x)
{
if(!rt) rt=++siz;
if(l==r) return;
int mid=(l+r)>>1;
if(x<=mid) add(ls[rt],l,mid,x);
else add(rs[rt],mid+1,r,x);
}
void extend()
{
for(int i=0;i<n;i++){
int c=s[i]-'a'+1;
int p=last,cur=++tot;
len[cur]=len[p]+1;
add(root[cur],1,n,len[cur]);//这相当于把以它结尾的最长串的endpos放进去
while(p!=-1 && !ch[p][c]){
ch[p][c]=cur;
p=link[p];
}
if(p==-1) link[cur]=0;
else{
int q=ch[p][c];
if(len[q]==len[p]+1) link[cur]=q;
else{
int copy=++tot;
link[copy]=link[q];
len[copy]=len[p]+1;
for(int i=1;i<=26;i++) ch[copy][i]=ch[q][i];
while(p!=-1 && ch[p][c]==q){
ch[p][c]=copy;
p=link[p];
}
link[cur]=link[q]=copy;
}
}
last=cur;
}
for(int i=1;i<=tot;i++) son[link[i]].push_back(i);
}//构造sam
bool judge(int rt,int l,int r,int ql,int qr)
{
if(!rt) return 0;
if(ql<=l&&r<=qr) return 1;
int mid=(l+r)>>1;
bool res=0;
if(ql<=mid) res=res|judge(ls[rt],l,mid,ql,qr);
if(res) return 1;
if(qr>mid) res=res|judge(rs[rt],mid+1,r,ql,qr);
return res;
}
int merge(int x,int y)
{
if(!x) return y;
if(!y) return x;
int rt=++siz;
ls[rt]=merge(ls[x],ls[y]);
rs[rt]=merge(rs[x],rs[y]);
return rt;
}
void dfs(int x)
{
for(int y:son[x]){
dfs(y);
root[x]=merge(root[x],root[y]);//取并集
}
}
signed main()
{
scanf("%s",s);
n=strlen(s);
link[0]=-1;
extend();
dfs(0);
int T;T=read;
int ql,qr,p;
char t[N<<1];
while(T-->0)
{
ql=read;qr=read;p=0;
scanf("%s",t+1);
m=strlen(t+1);
int end=m+1;
for(int i=1;i<=m+1;i++){//遍历到m+1，因为如果所有位都匹配上了，我们显然还要再找一位才能使字典序大于t
ans[i]=-1;
//遍历到前i位匹配
for(int c=max(1,t[i]-'a'+1+1);c<=26;c++){
//因为字典序要严格大于t，所以从t[i]-'a'+2开始
int v=ch[p][c];
if(v && judge(root[v],1,n,ql+i-1,qr)){
ans[i]=c;
break;
}
}
p=ch[p][t[i]-'a'+1];
if(!p || !judge(root[p],1,n,ql+i-1,qr)){
end=i;
break;
}
}
while(ans[end]==-1 && end) end--;
if(!end) puts("-1");
else{
for(int i=1;i<end;i++) putchar(t[i]);
putchar(ans[end]+'a'-1);pt;
}
}
return 0;
}
本人刚学 \(SAM\)，题解存在疏漏还请指出(拜谢
