CF1480C Searching Local Minimum

传送门

---

题意

交互
给定\(n\)， 有一个\(1-n\)的排列， 每次你可以询问\(x\)位置的数， 询问次数不超过\(100\)
求任意一个位置k， 使得\(a_k < \min(a_{k-1}, a_{k+1})\), 我们认为\(a_0=a_{n+1}= +\infty\)

题解

非常炫酷的交互！

当你看到题目的时候， 1e5的排列， 只能询问一个数， 而非某个区间的权值~！！！
只能100次， 结果几乎没有单调性， 完全独立，那不是酷毙了！！！让人有一种十分想切得感觉

炫酷题

---

显然大概是要二分啥的 ， 问题在于某个位置的数， 并没有单调性
没有单调性， 那我们就给他创造单调性！，.....emm创造不出来
那么是不是由于没有单调性的情况非常简单？单独解决掉没有单调性的的情况后就有单调性了？....
唉对， 如果不是特殊构造的数据， 那么一个数比相邻得数小应该很常见吧

经过这样的思考，您会开始考虑：
如果\(a_2 > a_1\) 直接输出1，\(a_{n-1} > a_n\) 直接输出n，
除此之外， a数组一开始必然下降， 最后必然上升， 那么整个数组必然如此：

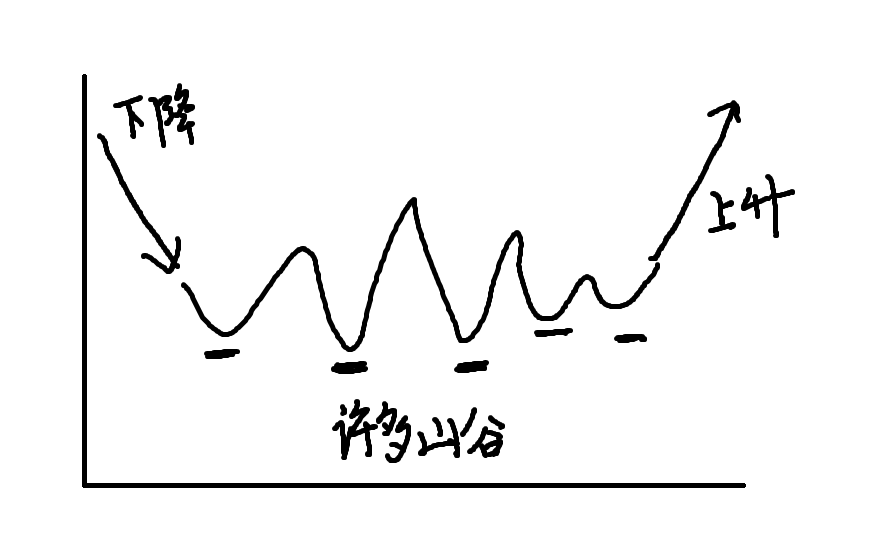
显然， 每个山谷都能成为答案，也只有山谷能成为答案

这时候， 你应该想到三分， 只有一个山谷显然可以三分， 复杂度也接近
一种想当然的想法是， 直接三分必然会趋近其中一个山谷， 得到答案
事实证明： 大多数情况也是如此， 并且会得到一个wrong on test61的罚时

---

关于三分法本质的探究和一种解决方案

为什么会wa呢， 我们来考虑一种情况

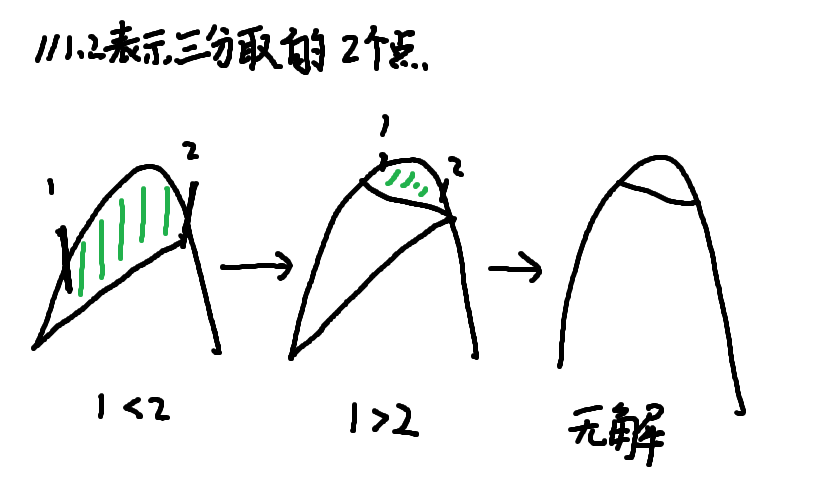
难道是因为我们没有判断左右两边导致的？但事实上这种情况也同样会导致

所以我们的做法假了为什么会假呢？这时候我们要考虑三分法本质
对于单谷函数， 每次取两个点假如是这样

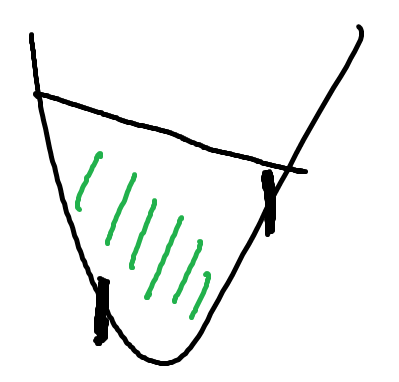
这两个点呈上升趋势， 山谷要么在两点之间， 要么在两点左边， 我们把右边界缩小到第二个点， 实质上是在定位山谷

在有多个山谷时， 这种单调性依然成立！

wa的原因实际上是因为在有多个山谷的时候， 几次三分定位的山谷不同

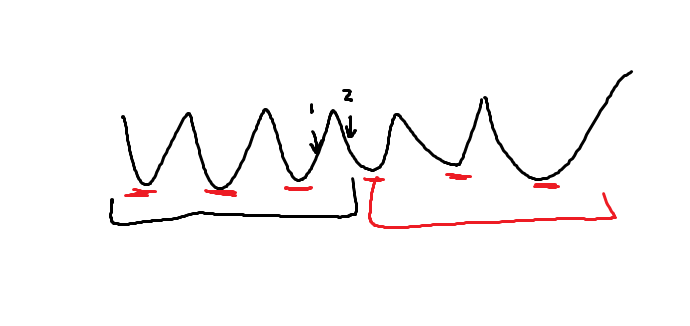
更准确的来说， 每次三分（见上图）实际上是定位了若干个山谷（左边黑色部分）， 抛弃了一些山谷（红色部分）
仔细思考， 我们只要避免之后的定位定位到抛弃的山谷即可

---

运用跳跃的思维， 您会得到一种解决方案

我们记录每次询问交互库得到的最小值， 以及所在的位置
假如在某次三分中，取到两个点都大于最小值，分类讨论：

如果两个点都在最小值左边， 将左端点设成三分取的第二个点
都在右边，就把右端点设成第一个点
在两点之间， 显然中间存在山谷， 让左端点等于第一个点， 右端点等于第二个点

这样做是没有问题的， 可以保证能够定位到某个山谷， 但是为什么不会定位到被抛弃的山谷呢？
假如某一时刻是这样的

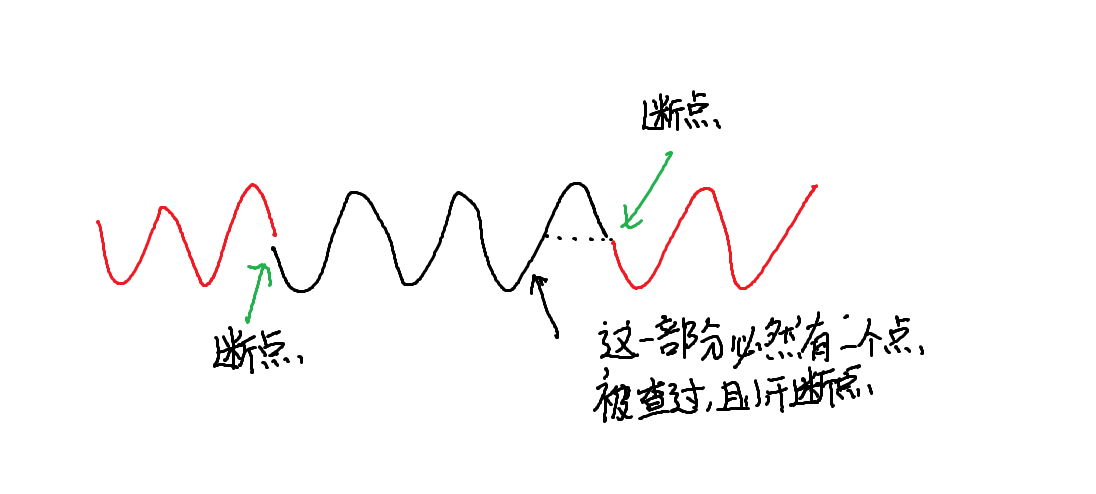
在这张图里面， 每个断点会被断开， 是因为它们右边或边必然存在一个点比他小，
如果要定位到一个被抛弃的山谷， 显然只有两个点都在下图灰色部分中

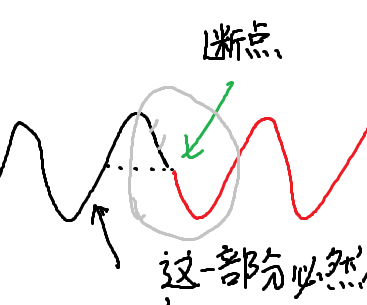
这时候两个点都会比断点大， 而记录的最小值一定小于断点， 所以， 这时候会定位到他们左边， 而非抛弃山谷

时间复杂度当然也是对的， 因为每次出现这个情况， 长度都会缩小到原来的三分之一

很妙啊

---

Impl

int l=1, r=n;
    int minp=-1, minv=0x3f3f3f3f;
	// 感谢@wzx大佬的hack， 这里不能将初始值设为n， 要设为正无穷
    while(l < r){
        int mid = (r-l+1)/3;
        int lmid=min(r, l+mid), rmid=max(l, r-mid);
        if(lmid > rmid) swap(lmid, rmid);
        if(lmid == rmid){
            if(lmid > l) lmid--;
            else rmid++;
        }

        int lans=get(lmid), rans=get(rmid);

        if(min(lans, rans) > minv){
            if(rmid < minp){
                l = rmid+1;
            }else if(lmid > minp){
                r = lmid-1;
            }else{
                l=lmid+1, r=rmid-1;
            }
        }else {
            if(lans < rans) minv=lans, minp=lmid;
            else minv=rans, minp=rmid;
        }

        if(lans < rans) r = rmid-1;
        else l = lmid+1;
    }
    pri(l);