CF1504D D. 3-Coloring

传送门

---

题意

交互
你需要用1，2，3三种颜色给一个\(n*n\)的网格染色， 每局对手会ban掉一个颜色不能使用。
你需要在\(n^2\)轮之后对整个图染色， 使得不存在相邻格子被染成相同颜色
可以证明， 存在必胜策略。

题解

你想想想看大概的思路， 首先相邻格子颜色不同， 那我们可以把颜色相同都放在一条斜线上，他们就不会相邻
然后再仔细想想看， 三个ban一个有什么性质: 比如说在每一轮我们至少可以用1，2中的一种颜色。

继续考虑， 我们得到一个大概的思路， 我们想要间隔的把每一斜列染成1， 2，

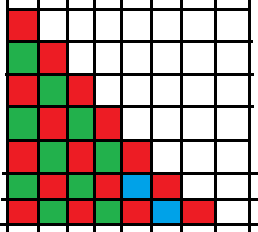
我们用黄绿蓝表示1， 2， 3

假如可以用1我就填1， 不能就填2，
最后要么全部填完， 要不就填完一种， 另一种一直被ban，填不满
那么这时候我们把没填完的都填3

宁仔细想想看， 显然是对的。

---

Impl

#include <iostream>
#include <cstdio>
#include <vector>
#include <cstdlib>
using namespace std;

int read(){
    int num=0, flag=1; char c=getchar();
    while(!isdigit(c) && c!='-') c=getchar();
    if(c == '-') c=getchar(), flag=-1;
    while(isdigit(c)) num=num*10+c-'0', c=getchar();
    return num*flag;
}

const int N = 1000;
int T, n;
int t1=1, p1=0, t2=2, p2=0;
vector<pair<int, int> > t[N]; 
int vis[N][N];

int wx=1, wy=1;

void solve(int x){
    if(t1>=2*n || t2>=2*n){
        while(vis[wx][wy]){
        	wy++;
        	if(wy > n) wx++, wy=1;
        	if(wx > n) return ;
		}
		vis[wx][wy]=1;
        cout << ((t1>=2*n)?(x==3?2:3):(x==3?1:3)) << ' ' << wx << ' ' << wy << '\n';
        cout.flush();
        return ;         
    }else{
        if(x == 1){
            int xp=t[t2][p2].first, yp=t[t2][p2].second;
            cout << 2 << ' ' << xp << ' ' << yp << '\n';
            cout.flush();
            vis[xp][yp]=1;p2++;
            if(p2 >= t[t2].size()) p2=0, t2+=2;
        }else{
            int xp=t[t1][p1].first, yp=t[t1][p1].second;
            cout << 1 << ' ' << xp << ' ' << yp << '\n';
            cout.flush();
            vis[xp][yp]=1;p1++;
            if(p1 >= t[t1].size()) p1=0, t1+=2;
        }     
    }
}
int main(){
    n=read();
    for(int i=1; i<2*n; i++){
        for(int j=1; j<=min(n, i); j++){
            if(i+1-j>n) continue;
            t[i].push_back(make_pair(j, i+1-j));
        }
    }
    for(int i=1; i<=n*n; i++){
        int x; cin >> x;
		solve(x);
    }
    return 0;
}