探究排序树分治 研究性学习

探究排序树分治 研究性学习

---

我们首先来看看归并排序和线段树


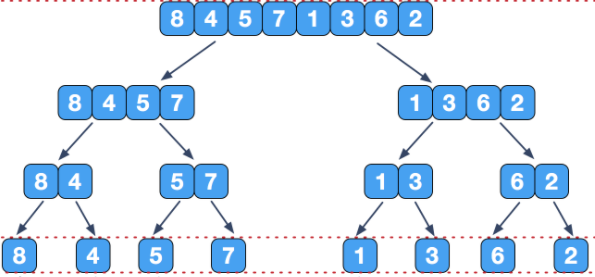
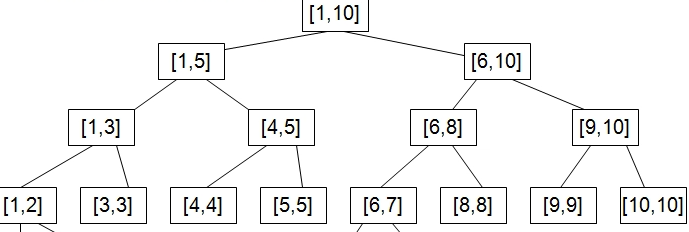
我们发现：在递归结构上，归并排序与线段树极为相似。
这是因为它们都用到了分治的思想。同时他们还有一个共同的操作：合并（归并）
归并排序通过把两个有序的数组合并成一个来排序，如果把过程想像成一颗树， 那么两个子节点就表示两个子数组的排序结果。
这与线段树的含义是一致的。而相较于归并排序， 线段树则可以直接查询某一个区间\([l, r]\)的结果， 而归并排序则不能直接查询\([l, r]\)的排序结果。不难想到我们可以利用可持久化的思想将每一次归并的结果作为节点来建立线段树， 以实现区间查询。

---

这就是排序树。
当然排序树在竞赛中的作用通常不是直接查询区间有序数组。
这是因为排序树的归并操作无法像线段树一样， 其时间复杂度达到了\(O(n)\)，从而导致总复杂度爆炸。

---

分治优化

进一步考虑， 我们发现排序树解决的大多是一些区间二分问题。
这一类问题需要我们多次在某一特定无序区间进行二分， 而二分则要求具有单调性， 每次都排序的复杂度显然不正确。
这时候考虑使用排序树。
朴素的排序树显然是不行的， 但我们可以发现一个神奇的性质，假如询问区间由多个单调子区间组成， 那么可以进行分治，
在每一个子区间中分别二分， 最后合并答案。
这时候不难发现： 这种二分结构实质上就是排序树的结构！
也就是说在排序树进行区间查询是， 将朴素的线段树合并改为分治， 最后合并答案。这样就可以完美的解决这一类问题了。

---

复杂度分析

由归并排序的时间复杂度可以发现， 排序树的空间复杂度实际上是\(O(nlogn)\)， 而每次查询时由于朴素线段树的复杂度为\(O(logn)\)
，合并时二分的复杂度为\(O(logn)\), 所以每次查询的时间复杂度是\(O(log^2n)\)
另一方面由于排序树实际应用时，多用于二分答案的check， 所以解决实际问题的复杂度期望为\(O(nlog^3n)\)