B+ Tree(数据库)
线性稀疏索引(Kafka)
-
适用于 append only 的存储模式,利用有序性带来的二分搜索,加速查找指定 offset 的日志内容
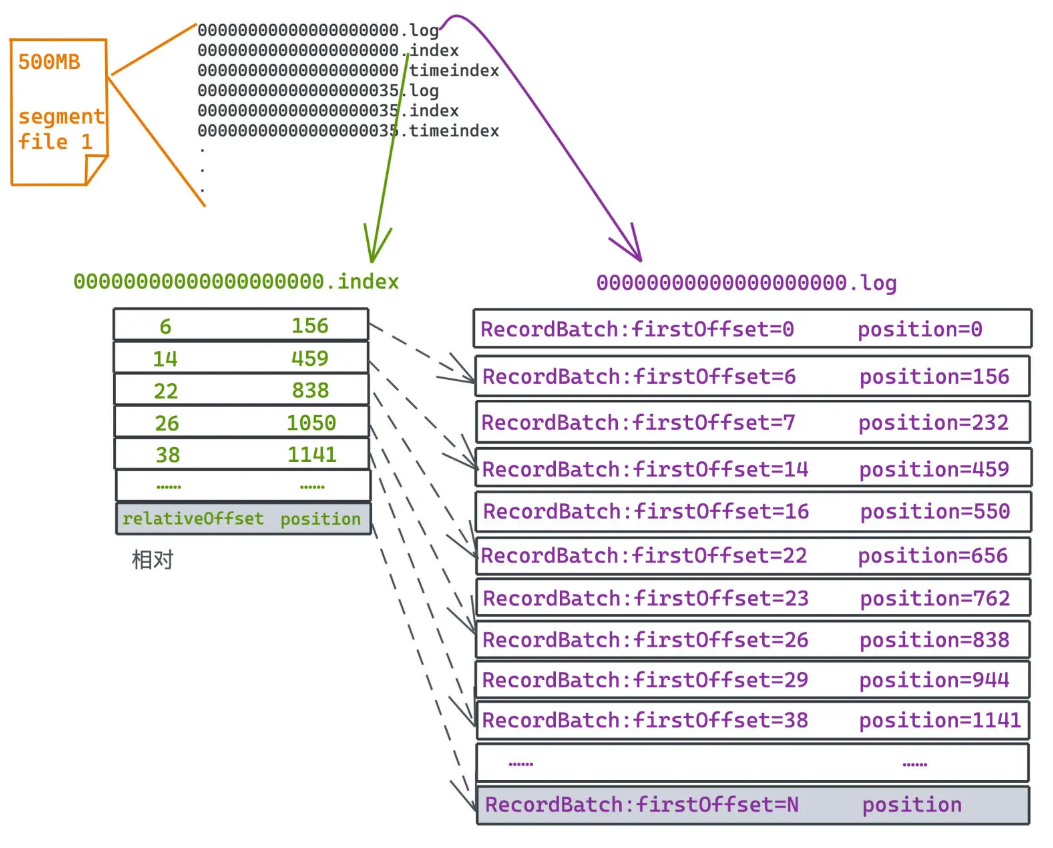
树状索引
红黑树

特点
-
在内存中,红黑树任意字段的查询可以做到 logN 的复杂度
-
相比于二分搜索所需具备的有序性,在红黑树上做元素的调整和增删效率要高得多。对于百万量级的存储场景,红黑树也只需要 20 层这个数量级的高度就可以容纳全部元素。查询效率很有保证
可以在数据库的索引中采用红黑树吗?
-
在数据库中,不同于内存的场景,磁盘读写比内存慢的多,所以相比于查询的计算成本,IO 成本可能要显著的多
-
数据库存储的数据比较多,若采用二叉树来存储的话,层数必然不会很少,且层和层之间的数据在物理上基本上是不连续的,即使前几层的元素可以被预加载至内存中,仍然可能需要在树上进行 10 余次的跳转查询,也就对应着 10 余次的磁盘 IO,这是不可接受的
B- 树
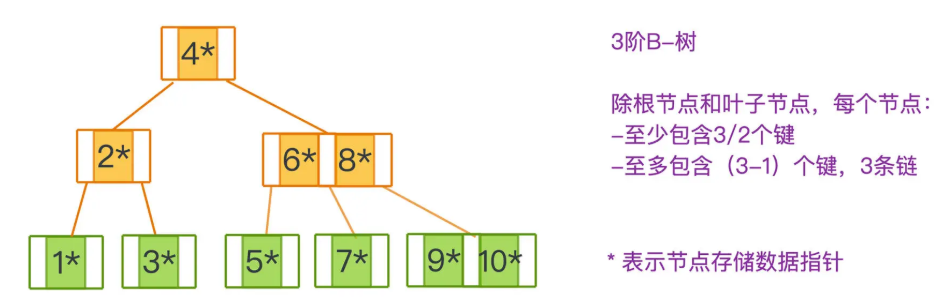
特点
-
每个节点都包含若干个键和若干个指针域,指针域就用于指向存储的数据本身。
-
所有叶子结点处于同一高度
-
除了根结点和叶子结点之外,每个节点最少包含 m/2 个键
-
每个节点最多包含 m-1 个键和 m 条链,如果某个节点有 k-1 个键,则对应 k 条链
-
每个节点内部的键有序排列,每个链指向的节点中的键,都在链左右节点的确定范围之间
-
根节点在不为叶子节点的时候至少有两个子节点
磁盘访问的局部性原理
若把 B- 树的每个节点中存储的大小设成一个页的大小,利用磁盘预读的能力,就可以做到仅通过一次 IO 就将整个节点的全部内容加载到内存中
-
一个页的大小通常是 4K~16K,能包含的键数可以高达几千条。以 InnoDB 通常采用的 16K 大小的页为例,若索引字段和指针域大小为 8B,B- 树上的每个节点能包含的键数高达 2048 个,这就意味着用 4 层的高度,就可以存储接近 10 亿级别的记录,在索引字段大小更大的时候,通常也只需要 5 层以内,就可以构造大部分表的索引
-
因为每个节点中的键是有序存储的,当我们加载到内存中后,通常也会直接采用二分搜索,整个搜索过程仍然是 logN 这样非常低的复杂度。所以主要耗时还是花费在 IO 中
B+ 树
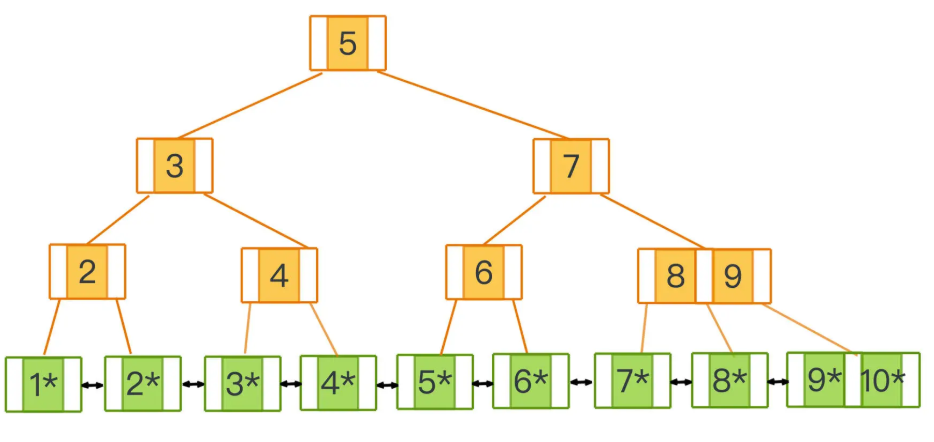
特点
-
B+ 树的所有的叶子节点之间会通过双向指针串联在一起,构成一个双向链表
-
B+ 树的中间节点不会存储数据指针,而只有叶子节点才会存储,中间节点只用于存储到叶子节点的路由信息
为什么要引入额外的指针和约束呢?
- 在数据库中经常需要范围查询,借助双向链表高效的范围查询


