模板
一.字符串
0.hash
没学过hash,从头到尾什么都不会
1.kmp

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48) ; if(f)x=-x; } const int maxn=1e6+6; int n,m,p[maxn]; char s[maxn],ss[maxn]; inline void pre() { int j=0; p[0]=-1; inc(i,0,m-1) { j=p[i]; while(j!=-1&&ss[i]!=ss[j])j=p[j]; p[i+1]=((~j)?(ss[i]==ss[j]?++j:0):0); } } inline void kmp() { int j=0; inc(i,0,n-1) { while(j!=-1&&s[i]!=ss[j])j=p[j]; ++j; if(j==m) { printf("%d\n",i+1-j+1); j=p[j]; } } } int main() { freopen("a.in","r",stdin); scanf("%s%s",s,ss); n=strlen(s);m=strlen(ss); pre(); kmp(); inc(i,1,m) printf("%d ",p[i]); re 0; }
2.trie
01trie

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48) ; if(f)x=-x; } const int maxn=1e5+5; int n,m,hd[maxn]; struct node{ int to,nt,val; }e[maxn<<1]; int k; inline void add(int x,int y,int z) { e[++k]=(node){y,hd[x],z};hd[x]=k; } int dis[maxn]; inline void dfs(int x,int fa) { for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(v==fa)continue; dis[v]=dis[x]^e[i].val; dfs(v,x); } } #define dec(i,l,r) for(int i=l;i>=r;--i) int tr[maxn*30][2],tot,ans; inline void insert(int x) { int u=0; dec(i,30,0) { int now=(x>>i)&1; if(!tr[u][now])tr[u][now]=++tot; u=tr[u][now]; } } inline void find(int x) { int u=0; int cnt=0; dec(i,30,0) { int now=(x>>(i))&1; if(tr[u][now^1]) { cnt+=1<<i; u=tr[u][now^1]; } else u=tr[u][now]; } ans=max(ans,cnt); } int main() { freopen("a.in","r",stdin); rd(n); int x,y,z; inc(i,2,n) { rd(x),rd(y),rd(z); add(x,y,z); add(y,x,z); } dfs(1,0); inc(i,1,n) { find(dis[i]); insert(dis[i]); } printf("%d",ans); re 0; }
trie的字符版就看看ac自动机就好了
3.ac自动机

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=1e6+6; int n,m,tr[maxn][26],tot,ed[maxn]; char s[maxn]; inline void insert() { int len=strlen(s+1),u=0,x; inc(i,1,len) { x=s[i]-'a'; if(!tr[u][x])tr[u][x]=++tot; u=tr[u][x]; } ++ed[u]; } int fail[maxn*26]; inline void Get_fail() { int u=0; queue<int>q; inc(i,0,25)if(tr[u][i])q.push(tr[u][i]); while(!q.empty()) { u=q.front(); q.pop(); inc(i,0,25) if(tr[u][i]) fail[tr[u][i]]=tr[fail[u]][i],q.push(tr[u][i]); else tr[u][i]=tr[fail[u]][i]; } re ; } int ans; inline void Get_A() { int len=strlen(s+1); int u=0; inc(i,1,len) { int x=s[i]-'a'; u=tr[u][x]; for(int t=u;t&&ed[t]!=-1;t=fail[t]) ans+=ed[t],ed[t]=-1; } } int main() { freopen("a.in","r",stdin); rd(n); inc(i,1,n) { scanf("%s",s+1); insert(); } Get_fail(); scanf("%s",s+1); Get_A(); printf("%d",ans); re 0; }
4.manacher
二.图论
1.最小生成树
Kruskal算法

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=5e3+3,maxm=2e5+5; int n,m; struct node{ int fr,to,val; inline bool operator<(node b)const { re val<b.val; } }e[maxm<<1]; int k,fa[maxn]; inline void add(int x,int y,int z){e[++k]=(node){x,y,z};} inline int find(int x){ re fa[x]==x?x:fa[x]=find(fa[x]); } int main() { freopen("a.in","r",stdin); rd(n),rd(m); int x,y,z; inc(i,1,m) { rd(x),rd(y),rd(z); add(x,y,z); } sort(e+1,e+k+1); inc(i,1,n)fa[i]=i; int cnt=0,ans=0; inc(i,1,k) { int x=find(e[i].fr),y=find(e[i].to); if(x!=y) { fa[x]=y; ans+=e[i].val; ++cnt; if(cnt==n-1)break; } } if(cnt==n-1)printf("%d",ans); else puts("-1"); re 0; }
prim算法
适合稠密图的prim

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=5e3+3,maxm=2e5+5; int inf=5e8; int n,m,d[maxn][maxn],dis[maxn],vis[maxn]; int main() { freopen("a.in","r",stdin); rd(n),rd(m); int x,y,z; inc(i,1,n)inc(j,1,n)d[i][j]=inf; inc(i,1,m) { rd(x),rd(y),rd(z); d[x][y]=d[y][x]=min(d[x][y],z); } vis[1]=1; inc(i,2,n)dis[i]=d[1][i]; int ans=0,cnt=n-1; while(cnt--) { int now,minn=inf; inc(i,1,n) if(!vis[i]&&dis[i]<minn)minn=dis[i],now=i; vis[now]=1; ans+=dis[now]; inc(i,1,n)dis[i]=min(dis[i],d[now][i]); } printf("%d",ans); re 0; }
2.最短路
已经凉透了的spfa

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=1e4+5,maxm=5e5+5; int n,m,hd[maxn]; struct node{ int to,nt,val; }e[maxm<<1]; int k,s; inline void add(int x,int y,int z){ e[++k]=(node){y,hd[x],z};hd[x]=k; } #define ll long long ll inf=2147483647,dis[maxn],vis[maxn]; inline void spfa() { inc(i,1,n)dis[i]=inf; dis[s]=0; queue<int>q; q.push(s); while(!q.empty()) { int x=q.front(); q.pop(); vis[x]=0; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(dis[v]>dis[x]+e[i].val) { dis[v]=dis[x]+e[i].val; if(!vis[v]) { vis[v]=1; q.push(v); } } } } } int main() { freopen("a.in","r",stdin); rd(n),rd(m),rd(s); int x,y,z; inc(i,1,m) { rd(x),rd(y),rd(z); add(x,y,z); } spfa(); inc(i,1,n)printf("%lld ",dis[i]); re 0; }
非常好看且实用的dijkstra

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=1e4+5,maxm=5e5+5; int n,m,hd[maxn]; struct node{ int to,nt,val; }e[maxm<<1]; int k,s; inline void add(int x,int y,int z){ e[++k]=(node){y,hd[x],z};hd[x]=k; } #define ll long long ll inf=2147483647,dis[maxn]; struct KKK{ int x,val; inline bool operator<(KKK u)const { re val>u.val; } }; inline void dij() { inc(i,1,n)dis[i]=inf; dis[s]=0; priority_queue<KKK>q; q.push((KKK){s,0}); while(!q.empty()) { KKK u=q.top(); q.pop(); int x=u.x; if(dis[x]!=u.val)continue; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(dis[v]>dis[x]+e[i].val) { dis[v]=dis[x]+e[i].val; q.push((KKK){v,dis[v]}); } } } } int main() { freopen("a.in","r",stdin); rd(n),rd(m),rd(s); int x,y,z; inc(i,1,m) { rd(x),rd(y),rd(z); add(x,y,z); } dij(); inc(i,1,n)printf("%lld ",dis[i]); re 0; }
玄学暴力的floyd

inc(k,1,n) inc(i,1,n) inc(j,1,n) d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
3.树的直径
不好找路径的树形DP

inline void dfs(int x,int fa) { for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to,w=e[i].val; if(v==fa)continue; dfs(v,x); if(d0[v]+w>d2[x]) { d2[x]=d0[v]+w; if(d2[x]>d1[x]) { swap(d2[x],d1[x]); if(d1[x]>d0[x]) swap(d0[x],d1[x]); } } } ans=max(ans,d0[x]+d1[x]); } inline void dfs2(int x,int fa) { ans=max(ans,g[x]+d0[x]); for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(v==fa)continue; g[v]=g[x]+e[i].val; dfs2(v,x); } }
弄不好负权的两次dfs

inline void dfs(int x,int fa) { if(dis[x]>maxx)maxx=dis[x],p=x; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(v=fa)continue; dis[v]=dis[x]+e[i].val; dfs(v,x); } }
4.树的最近公共祖先
1.倍增

inline void dfs(int x) { for(int i=1;fa[fa[x][i-1]][i-1];++i) fa[x][i]=fa[fa[x][i-1]][i-1]; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(v==fa[x][0])continue; fa[v][0]=x; deep[v]=deep[x]+1; dfs(v); } } inline int LCA(int x,int y) { if(deep[x]<deep[y])swap(x,y); dec(i,20,0) if(deep[fa[x][i]]>=deep[y]) { x=fa[x][i]; } if(x==y)re x; dec(i,20,0) if(fa[y][i]!=fa[x][i]) { x=fa[x][i]; y=fa[y][i]; } re fa[x][0]; }
2.树链剖分

inline void dfs1(int x,int fa) { siz[x]=1; deep[x]=deep[fa]+1; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(v==fa)continue; dfs1(v,x); siz[x]+=siz[v]; if(siz[v]>siz[son[x]])son[x]=v; } } inline void dfs2(int x,int fp) { top[x]=fp; rev[seg[x]=++tot]=x; if(son[x]) { dfs2(v,fp); bot[x]=bot[son[x]]; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(!top[v])dfs2(v,v); } } else bot[x]=x; } inline void LCA(int x,int y) { while(top[x]!=top[y]) { if(deep[top[x]]<deep[top[y]])swap(x,y); x=fa[top[x]]; } if(deep[x]>deep[y])swap(x,y); re x; }
3.tarjan
+并查集

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=5e5+5; int n,m,s; int hd[maxn],hd1[maxn]; struct node{ int to,nt; }e[maxn<<1]; struct nide{ int q1,ans,id,nt; inline bool operator<(nide b)const{ re id<b.id;} }q[maxn]; int k,k1=1; inline void add(int x,int y){e[++k]=(node){y,hd[x]};hd[x]=k;} inline void addq(int x,int y){q[++k1]=(nide){y,0,k1,hd1[x]};hd1[x]=k1;} int vis[maxn],fa[maxn]; inline int find(int x){re x==fa[x]?x:fa[x]=find(fa[x]);} inline void dfs(int x,int pre) { vis[x]=1; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(v==pre)continue; dfs(v,x); fa[v]=x; } for(int i=hd1[x];i;i=q[i].nt) { int v=q[i].q1; if(!vis[v]||q[i].ans)continue; else q[i].ans=q[i^1].ans=find(v); } } int main() { freopen("a.in","r",stdin); rd(n);rd(m);rd(s); int x,y; inc(i,1,n)fa[i]=i; inc(i,2,n) { rd(x),rd(y); add(x,y);add(y,x); } inc(i,1,m) { rd(x),rd(y); addq(x,y),addq(y,x); } dfs(s,0); sort(q+1,q+k1+1); for(int i=2;i<=k1;i+=2) { printf("%d\n",q[i].ans); } re 0; }
5.树上差分
点的差分:cnt(s)++,cnt(t)++,cnt(lca)--,cnt(falca)--;
边的差分:cnt(s)++,cnt(t)++,cnt(lca)-2;【cnt代表其父到他的路径】
然后跑一边dfs遍历全树
6.差分约束
7.tarjan系列大礼包
1.割点(对于无向图G,删除节点x以及与x相连的边,会分裂两个图的节点x)
if(low[v]>=dfn[x]) { ++siz; if(rt!=x||siz>1)g[x]=1; }

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=2e4+4,maxm=1e5+5; int n,m,hd[maxn],g[maxn]; struct node{ int to,nt; }e[maxm<<1]; int k=1; inline void add(int x,int y){ e[++k]=(node){y,hd[x]};hd[x]=k; } int dfn[maxn],low[maxn],tot,rt; inline void tarjan(int x,int E) { dfn[x]=low[x]=++tot; int siz=0; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(i==(E^1))continue; if(!dfn[v]) { tarjan(v,i); low[x]=min(low[x],low[v]); if(low[v]>=dfn[x]) { ++siz; if(rt!=x||siz>1)g[x]=1; } } else low[x]=min(low[x],dfn[v]); } } int main() { freopen("a.in","r",stdin); rd(n),rd(m); int x,y; inc(i,1,m) { rd(x),rd(y); add(x,y); add(y,x); } inc(i,1,n) if(!dfn[i])rt=i,tarjan(i,0); int cnt=0; inc(i,1,n)if(g[i])++cnt; printf("%d\n",cnt); inc(i,1,n) if(g[i])printf("%d ",i); re 0; }
2.桥(对于无向图G,删除边E,会变成两个图的边E)
if(i==(E^1))continue;
if(low[v]>dfn[x])bridge[i]=beidge[i^1]=1;

inline void tarjan(int x,int E) { dfn[x]=low[x]=++tot; int siz=0; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(i==(E^1))continue; if(!dfn[v]) { tarjan(v,x); if(low[v]>dfn[x]) bridge[i]=beidge[i^1]=1; } else low[x]=min(low[x],dfn[v]); } }
3.点双(由孤立节点和其他点双连通分量组成)
!!!割点可能属于多个v_dcc,但其他的点只属于一个
!!!顺便求出割点(缩点有用)
求取

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } int rt,dfn[maxn],low[maxn],tot,s[maxn],stop; vector<int>v_dcc[maxn],v_cnt; inline void tarjan(int x) { dfn[x]=low[x]=++tot; s[++stop]=x; if(rt==x&&!hd[x])//孤立点 { v_dcc[++v_cnt].push_back(x); --stop; re ; } int siz=0; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(!dfn[v]) { tarjan(v); low[x]=min(low[x],low[v]); if(low[v]>=dfn[x]) { ++siz; if(rt!=x||siz>1)cut[x]=1; ++v_cnt; while(s[stop+1]==v)//!!!!!!!!只能判v,因为y之前,x之后可能还有其他节点 { v_dcc[v_cnt].push_back(s[stop]); --stop; } v_dcc[v_cnt].push_back(x); } } else low[x]=min(low[x],dfn[v]); } } int main() { //…… inc(i,1,n) if(!dfn[i])rt=x,tarjan(i); }
缩点
给每个割点一个新的编号
建新图,从每个v_dcc到它包含的所有的割点连边
(在求取的基础代码的main函数中加入)

int main() { inc(i,1,n)if(!dfn[i])tarjan(i); int num=v_cnt; inc(i,1,n)if(cut[i])new_id[i]=++num; inc(i,1,v_cnt) inc(vector<int>::iterator it=v_dcc[i].begin();it!=v_dcc[i].end();++it){ int v=*it; if(cut[v]) { add(i,new_id[v]); add(new_id[v],i); } } re 0; }
4.边双
求取:删除所有桥的情况下,得到的所有连通块
可以用一个dfs

inline void dfs(int x) { c[x]=e_dcc for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(c[v]||bridge[i])continue; dfs(v); } } int main() { //…… tarjan(); inc(i,1,n) if(!c[i]) { ++e_dcc; dfs(i); } re 0; }
缩点:求取边双的情况下得到各个点所属的边双
if(c[x]==c[y])continue; else add(c[x],c[y])
也就是说新图的边就只剩下桥
重新建图就好
5.强连通

inline void tarjan(int x) { dfn[x]=low[x]=++tot; s[++stop]=x; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(!dfn[v]){ tarjan(v); low[x]=min(low[x],low[v]); } else if(!belong[v])low[x]=min(low[x],dfn[v]); } if(dfn[x]==low[x]) { ++col; while(s[stop+1]!=x) { belong[s[stop]]=col; --stop; } } }
6. 2-sat
8.判负环
在保证有负环的情况下用基于dfs的spfa可能要比基于bfs的spfa要快一点
然而,我不会
暴力选手LL泪流满面
只能跑n遍spfa
9.基环树
我做过的大概就是两个思路
当然是针对环处理的
首先找出环
1.转成环形dp
2.强制断开某条边
代码什么的都太烦了
提供三个找环的方向
a.toposort 可以在预先将非环点处理同时 通过未访问过的点得到环
b.dfs爆搜,遇到访问过的点逆回(因为基环树只可能有一个环)
c.使用并查集,然而不幸的是你只能得到每个环上的一双点与一条边
10.二分图
奇环

inline bool dfs(int x,int col) { c[x]=col; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(c[v]==col)re 1; else if(c[v]==-1)dfs(v,col^1); } } int main() { memset(c,-1,sizeof c); //找奇环 inc(i,1,n) { if(!c[i])dfs(c[i]); //存在奇环 //且包括包括奇环的环也可分为奇环 //实用于判断有无奇环 //以及tarajan } re 0; }
最大匹配

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=1005; int n,m,hd[maxn],belong[maxn],vis[maxn]; struct node{ int to,nt; }e[maxn*maxn]; int k; inline void add(int x,int y) { e[++k]=(node){y,hd[x]};hd[x]=k; } inline bool vivi(int x) { for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(!vis[v]) { vis[v]=1; if(!belong[v]||vivi(belong[v])) { belong[v]=x; re 1; } } } re 0; } int main() { freopen("a.in","r",stdin); int E,x,y; rd(n),rd(m),rd(E) ; inc(i,1,E) { rd(x),rd(y); if(x>n||y>m)continue; add(x,y); } int ans=0; inc(i,1,n) { memset(vis,0,sizeof vis); ans+=vivi(i); } printf("%d",ans); }
呃,最大权值匹配KM算法就弄费用流吧
KM不常用,还有局限性,最主要是我背不到
背不到就是背不到,就算差不多我将高中语文必背都背完了,也背不到
还是放个板子

#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<cmath> #include<algorithm> #define re return #define ll long long #define inc(i,l,r) for(int i=l;i<=r;++i) const int inf=2147483647,maxn=305; using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } int n; int ex1[maxn];//1的期望度 int ex2[maxn];//2的期望度 int pri[maxn][maxn];//价格 int match[maxn];//匹配2的1 int vis1[maxn];//1是否被访问过 int vis2[maxn];//2是否访问过 int slack[maxn];//最小差多少,2可以被1访问 inline bool dfs(int x) { vis1[x]=1;//标记1访问 inc(i,1,n) { if(vis2[i])continue; if(ex1[x]+ex2[i]==pri[x][i])//达到访问要求 { vis2[i]=1;标记2访问 if(!match[i]||dfs(match[i])) { match[i]=x; re 1; } } else slack[i]=min(slack[i],ex1[x]+ex2[i]-pri[x][i]); //2差值统计 } re 0; } inline void KM() { inc(i,1,n)match[i]=ex2[i]=0; //刷新 inc(i,1,n) { inc(j,1,n) slack[j]=inf; while(2333) { inc(j,1,n)vis1[j]=vis2[j]=0; if(dfs(i))break; int d=inf; inc(j,1,n) if(!vis2[j]) d=min(d,slack[j]); //最小改变度 inc(j,1,n) { if(vis1[j])ex1[j]-=d; if(vis2[j])ex2[j]+=d; else slack[j]-=d; //分别改变 } } } } int main() { while(~scanf("%d",&n)) { inc(i,1,n)ex1[i]=-inf; inc(i,1,n) inc(j,1,n) { rd(pri[i][j]); ex1[i]=max(ex1[i],pri[i][j]); } int ans=0; KM(); for(int i=1;i<=n;++i) ans+=pri[match[i]][i]; printf("%d\n",ans); } re 0; }
最小点覆盖=最大匹配
最大独立集=节点总数-最小点覆盖=节点总数-最大匹配
有向无环图的最小点覆盖
11.欧拉回路
12.网络流
定理:最大流=最小割
最大流

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=1e4+4,maxm=1e5+5; int n,m,hd[maxn],s,t; struct node{ int to,nt,w; }e[maxm<<1]; int k=1; inline void add(int x,int y,int z) { e[++k]=(node){y,hd[x],z};hd[x]=k; e[++k]=(node){x,hd[y],0};hd[y]=k; } int deep[maxn],cur[maxn]; inline bool bfs() { inc(i,1,n)deep[i]=0; deep[s]=1; queue<int>q; q.push(s); while(!q.empty()) { int x=q.front(); q.pop(); for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to; if(!deep[v]&&e[i].w) { deep[v]=deep[x]+1; if(v==t)re 1; q.push(v); } } } re 0; } inline int dfs(int x,int flow) { if(x==t)re flow; int delta=flow; for(int &i=cur[x];i;i=e[i].nt) { int v=e[i].to; if(deep[v]==deep[x]+1&&e[i].w) { int d=dfs(v,min(e[i].w,delta)); e[i].w-=d;e[i^1].w+=d; delta-=d; if(!delta)re flow; } } re flow-delta; } int main() { //freopen("a.in","r",stdin); rd(n),rd(m),rd(s),rd(t); int x,y,w; inc(i,1,m) { rd(x),rd(y),rd(w); add(x,y,w); } int ans=0; while(bfs()) { inc(i,1,n)cur[i]=hd[i]; ans+=dfs(s,2147483647); } printf("%d",ans); re 0; }
费用流

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=5e3+3; int k=1,n,m,s,t; int dis[maxn],ord[maxn],hd[maxn],flow[maxn],vis[maxn]; int smoney,sflow; struct node{ int flow,to,nt,cost; }e[100005]; inline void add(int u,int v,int w,int f) { e[++k].to=v;e[k].nt=hd[u];e[k].flow=w;e[k].cost=f;hd[u]=k; } inline bool spfa() { queue<int>q; memset(dis,0x3f3f3f3f,sizeof dis); memset(vis,0,sizeof vis); q.push(s); dis[s]=0; flow[s]=0x3f3f3f3f; while(!q.empty()) { int x=q.front(); q.pop(); vis[x]=0; for(int i=hd[x];i;i=e[i].nt) { int v=e[i].to,w=e[i].flow,f=e[i].cost; if(w&&dis[v]>dis[x]+f) { if(!vis[v]) { vis[v]=1; q.push(v); } flow[v]=min(flow[x],w); dis[v]=dis[x]+f; ord[v]=i; } } } re dis[t]!=0x3f3f3f3f; } inline void vivi() { int x=t; while(x!=s) { int i=ord[x]; e[i].flow-=flow[t]; e[i^1].flow+=flow[t]; x=e[i^1].to; } sflow+=flow[t]; smoney+=flow[t]*dis[t]; } int main() { freopen("a.in","r",stdin); rd(n),rd(m),rd(s),rd(t); int u,v,w,f; inc(i,1,m) { rd(u),rd(v),rd(w),rd(f); add(u,v,w,f); add(v,u,0,-f); } while(spfa()) vivi(); printf("%d %d",sflow,smoney); re 0; }
三.高精度
四.数学
1.线性筛素数

#include<bits/stdc++.h> #define re return #define inc(i,l,r) for(int i=l;i<=r;++i) using namespace std; template<typename T>inline void rd(T&x) { char c;bool f=0; while((c=getchar())<'0'||c>'9')if(c=='-')f=1; x=c^48; while((c=getchar())>='0'&&c<='9')x=x*10+(c^48); if(f)x=-x; } const int maxn=1e7+5; int n,m,notprime[maxn],prime[maxn],p_cnt; inline void Get_prime() { notprime[1]=1; inc(i,2,n) { if(!notprime[i])prime[++p_cnt]=i; inc(j,1,p_cnt) { if(prime[j]*i>n)break; notprime[i*prime[j]]=1; if(i%prime[j]==0)break; } } } int main() { freopen("a.in","r",stdin); rd(n),rd(m); Get_prime(); int x; inc(i,1,m) { rd(x); if(notprime[x])puts("No"); else puts("Yes"); } re 0; }
2.欧几里得
inline int gcd(int a,int b){re b?gcd(b,a%b):a;}
3.扩展欧几里得
inline int exgcd(int a,int b,int &x,int &y) { if(!b){x=1,y=0;re a;} int d=exgcd(b,a%b,x,y); int t=x; x=y; y=t-a/b*y; re d; } int main() { //a*x+b*y=c; int a,b,x,y,c=1; rd(a),rd(b); int d=exgcd(a,b,x,y); if(c%d)printf("-1"); else x=x*c/d; //最小正整数 x=(x%b+b)%b; printf("%d",x); re 0; }
4.欧拉函数
单求
线性筛
5.欧拉定理
6.逆元
单求
费马小定理:如p是质数,且Gcd(a,p)=1,那么 a^(p-1) ≡1(mod p)
即a的逆元=>a^(p-2)
线性筛
inv[1]=1; inc(i,2,n)inv[i]=1ll*(P-P/i)*inv[P%i]%P; inc(i,1,n)printf("%d\n",inv[i]);
7.中国剩余定理
8.矩阵
9.高斯消元
10线性基
11.组合数
性质:
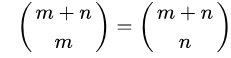
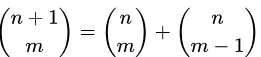
2^n=(n 0)+(n 1)+(n 2)+……+(n n)
二项式定理
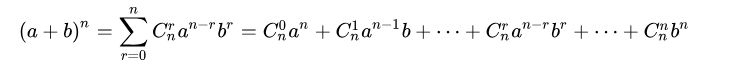
Lucas定理

ll jc[100005],p; inline ll pow(ll a,ll x) { ll ret=1; while(x) { if(x&1)ret=ret*a%p; a=a*a%p; x>>=1; } re ret; } inline ll C(ll n,ll m) { if(m>n)re 0; re jc[n]*pow(jc[m],p-2)%p*pow(jc[n-m],p-2); } inline ll LUCAS(ll n,ll m) { if(!m)re 1; re C(n%p,m%p)*LUCAS(n/p,m/p)%p; } int main() { //freopen("in.txt","r",stdin); int T; rd(T); while(T--) { jc[0]=1; ll n,m; rd(n),rd(m),rd(p); inc(i,1,p)jc[i]=jc[i-1]*i%p; printf("%lld\n",LUCAS(n+m,m)); } re 0; }
catalan数
n个0与n个1构成的序列方案数,使得任何一个前缀0的个数不少于1的个数
对于在n位的2进制中,有m个0,其余为1的catalan数为:C(n,m)-C(n,m-1)
12.0/1分数规划
13.博弈论


