二叉苹果树（由根分为左子树和右子树两部分情况）

有一棵二叉苹果树，如果数字有分叉，一定是分两叉，即没有只有一个儿子的节点。这棵树共  个节点，标号  至 ，树根编号一定为 。

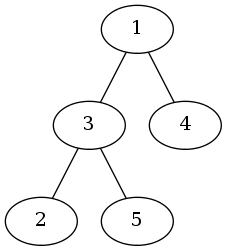
我们用一根树枝两端连接的节点编号描述一根树枝的位置。一棵有四根树枝的苹果树，因为树枝太多了，需要剪枝。但是一些树枝上长有苹果，给定需要保留的树枝数量，求最多能留住多少苹果。

输入格式

第一行两个数 N和 Q，N 表示树的节点数， Q表示要保留的树枝数量。

接下来 N-1行描述树枝信息，每行三个整数，前两个是它连接的节点的编号，第三个数是这根树枝上苹果数量。

输出格式

输出仅一行，表示最多能留住的苹果的数量。

---

 

f[i][j]表示当前节点保留j根树枝的最大苹果数

 

#include<bits/stdc++.h> 
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)
using namespace std;
template<typename T>inline void rd(T&x)
{
    char c;bool f=0;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
    x=c^48;
    while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
    if(f)x=-x; 
}


const int maxn=105; 
int n,m,k,f[maxn][maxn],hd[maxn];
struct node{
    int to,nt,val;
}e[10005];

inline void add(int x,int y,int z)
{
    e[++k].to=y;e[k].nt=hd[x];hd[x]=k;e[k].val=z;
    e[++k].to=x;e[k].nt=hd[y];hd[y]=k;e[k].val=z;
}

inline void dfs(int x,int fa,int add)
{
    int son1=0,son2=0;//左右儿子
    for(int i=hd[x];i;i=e[i].nt)
    {
        int v=e[i].to;
        if(v==fa)continue;
        if(!son1)son1=v;
        else son2=v;
        dfs(v,x,e[i].val);    
    }
    
    if(x!=1)//非根节点累计自身苹果树 
    {    
        inc(i,1,m)
        inc(j,0,i-1)
        f[x][i]=max(f[x][i],f[son1][j]+f[son2][i-1-j]+add);
    }
    else //根节点累计儿子苹果数 
    {
        inc(j,0,m)
        f[x][m]=max(f[x][m],f[son1][j]+f[son2][m-j]);
    }
    
}


int main()
{
    freopen("in.txt","r",stdin);
    int x,y,z;
    rd(n),rd(m);
    inc(i,2,n)
    {
        rd(x);rd(y);rd(z);
        add(x,y,z);
    }
    
    dfs(1,0,0);
        
    printf("%d",f[1][m]);
    re 0;
}