矩阵乘法之Fibonacci的进击

矩阵乘法的本质

矩阵乘法的定义

详见8.23的笔记

 

灵魂画手LL为您倾情演绎大型数学励志剧矩阵乘法之Fibonacci的进击

进击一之Fibonacci 第 n 项

 鉴于TinyMCE的玄学属性，以及Markdown抽风的LAtex

我决定手绘

 

 

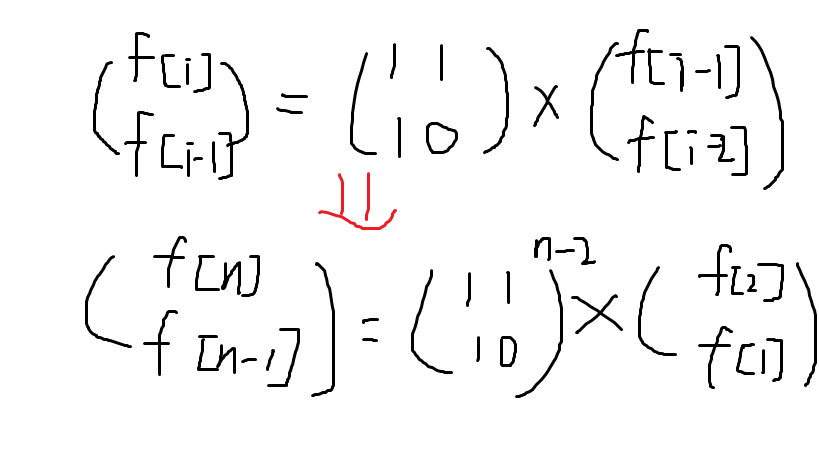
代码

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)

typedef long long ll;
using namespace std;
template<typename T>inline void rd(T&x)
{
    char c;bool f=0;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
    x=c^48;
    while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
    if(f)x=-x;
}

ll A[3][3],B[3][3],C[3][3];
ll n,m,mod;

//两个分开的矩阵乘法
inline void vivi()
{
    inc(i,1,2)inc(j,1,2)
    B[i][j]=C[i][j];
    
    memset(C,0,sizeof C);
    inc(i,1,2)inc(j,1,2)
    inc(k,1,2)
    C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod)%mod;
}

inline void cici()
{
    inc(i,1,2)inc(j,1,2)
    B[i][j]=A[i][j];
    
    memset(A,0,sizeof A);
    inc(i,1,2)inc(j,1,2)
    inc(k,1,2)
    A[i][j]=(A[i][j]+B[i][k]*B[k][j]%mod)%mod;
     
}

inline void Pow_Matrix(ll x)
//结合律，快速幂
{
    while(x)
    {
        if(x&1)vivi();
        cici();
        x>>=1;
    }
}

int main()
{
    rd(n),rd(mod);
    if(n==1||n==2)
    {
        printf("1");
        re 0;
    }
    
    A[1][1]=A[1][2]=A[2][1]=1;
    C[1][1]=C[2][2]=1; 
    //赋初值
    Pow_Matrix(n-2); 
    
    
    printf("%d",(C[1][2]+C[1][1])%mod);
    re 0;
}

 

进击二之Fibonacci 前 n 项和

再次手绘

Sn表示当前F[1]到F[n]的和

 

代码

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)

typedef long long ll;
using namespace std;
template<typename T>inline void rd(T&x)
{
    char c;bool f=0;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
    x=c^48;
    while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
    if(f)x=-x;
}

const int maxn=4,biu=3;
ll A[maxn][maxn],B[maxn][maxn],C[maxn][maxn];
ll n,m,mod=1000000007;


inline void vivi()
{
    inc(i,1,biu)inc(j,1,biu)
    B[i][j]=C[i][j];
    
    memset(C,0,sizeof C);
    inc(i,1,biu)inc(j,1,biu)
    inc(k,1,biu)
    C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod)%mod;
}

inline void cici()
{
    inc(i,1,biu)inc(j,1,biu)
    B[i][j]=A[i][j];
    
    memset(A,0,sizeof A);
    inc(i,1,biu)inc(j,1,biu)
    inc(k,1,biu)
    A[i][j]=(A[i][j]+B[i][k]*B[k][j]%mod)%mod;
     
}
inline void Pow_Matrix(ll x)
{
    while(x)
    {
        if(x&1)vivi();
        cici();
        x>>=1;
    }
}

int main()
{
    int T;
    rd(n);rd(mod);
        if(n<=3)
        {
            printf("1\n");
            re 0;
        }
    
        memset(A,0,sizeof A);
        memset(C,0,sizeof C);
        A[1][1]=A[1][2]=A[1][3]=A[2][3]=A[2][2]=A[3][2]=1;
        C[1][1]=C[2][2]=C[3][3]=1;
        
        Pow_Matrix(n-2); 
            
        printf("%lld\n",(C[1][1]*2+C[1][2]+C[1][3])%mod);
    
    
    re 0;
}

 

进击三之佳佳的 Fibonacci

title out talk:话说L佳佳,竟然如此热爱数学，日常%dalao

由于T[n]是收敛序列，不好构造递推式（一般收敛型或线性序列有递推式）

所以我们来构造

……（详情见小蓝书P421）

P[n]=n*S[n]-T[n];

S[n]同上

 

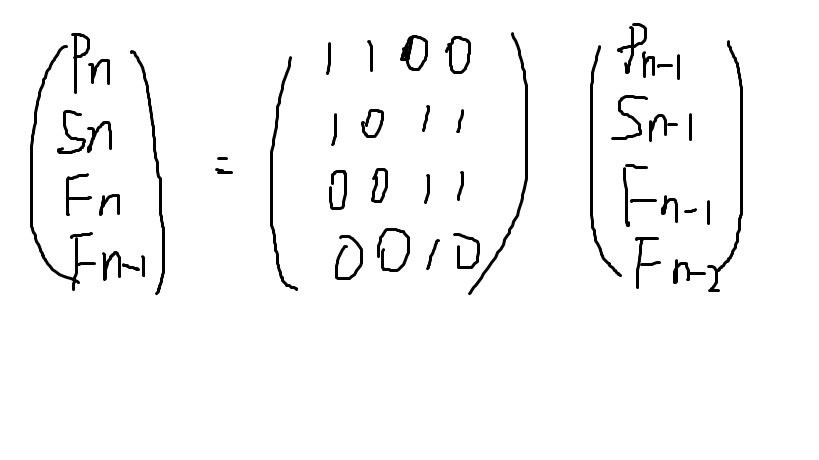
代码

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)

typedef long long ll;
using namespace std;
template<typename T>inline void rd(T&x)
{
    char c;bool f=0;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
    x=c^48;
    while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
    if(f)x=-x;
}

const int maxn=5,biu=4;
ll A[maxn][maxn],B[maxn][maxn],C[maxn][maxn];
ll n,m,mod=1000000007;


inline void vivi()
{
    inc(i,1,biu)inc(j,1,biu)
    B[i][j]=C[i][j];
    
    memset(C,0,sizeof C);
    inc(i,1,biu)inc(j,1,biu)
    inc(k,1,biu)
    C[i][j]=(C[i][j]+A[i][k]*B[k][j]%mod)%mod;
}

inline void cici()
{
    inc(i,1,biu)inc(j,1,biu)
    B[i][j]=A[i][j];
    
    memset(A,0,sizeof A);
    inc(i,1,biu)inc(j,1,biu)
    inc(k,1,biu)
    A[i][j]=(A[i][j]+B[i][k]*B[k][j]%mod)%mod;
     
}
inline void Pow_Matrix(ll x)
{
    while(x)
    {
        if(x&1)vivi();
        cici();
        x>>=1;
    }
}

int main()
{
    int T;
    rd(n);rd(mod);
        if(n<=2)
        {
            if(n==1)printf("1\n");
            else printf("3\n");
            re 0;
        }
    
        memset(A,0,sizeof A);
        memset(C,0,sizeof C);
        A[1][1]=A[1][3]=A[1][4]=A[2][1]=A[2][2]=1;
        A[3][3]=A[3][4]=A[4][3]=1;
        inc(i,1,biu)C[i][i]=1;
        
        Pow_Matrix(n-2); 
        
        ll P=0,S=0;
        inc(i,1,biu)
        {
            S+=C[1][i];
            P+=C[2][i];
        } 
        P=(P+C[2][1])%mod;S=(S+C[1][1])%mod;
        printf("%lld\n",(n%mod*S%mod-P+mod)%mod);
    
    
    re 0;
}